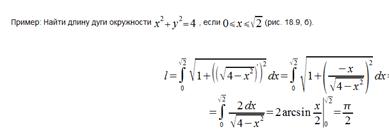Классификация ф-ций.
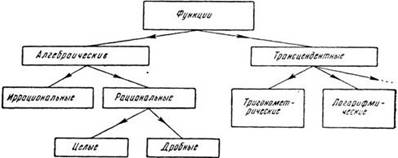
Функции заданные единой формулой классифицируются в зависимости от характера алгебр-х действий, кот. надо совершить над арг. что бы получить знач. ф-ции.
- Целорацион-ый многочлен (полином), если прим операции слож, умнож, возв в целую степень.
Прим. у=х3+3х²-5х
- Если к операц 1 добавит деление, то получ класс рацион ф-ций.
Прим. у=х4-3х²+1/(х-3)
-
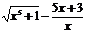 Е сли к перечисл опер доб извл корня то получ класс алгебр-х ф-ций
Е сли к перечисл опер доб извл корня то получ класс алгебр-х ф-ций
Прим.
Основные элементарные функции.
Основными элементарными функциями называются следующие: степенная, показательная, логарифмическая, тригонометрические, обратные тригонометрические (arcsin..) (поподробнее расписать с примерами и графиками).
1) у=const
2) у=хn, n? R – степенные ф-ции

3) у=ах, а>0, а≠1 – показательные ф-ции

4) у=logах, а>0, а≠1 – логарифмические ф-ции
а) Областью определения логарифмической функции является множество всех положительных чисел.
Это утверждение следует из определения логарифма, так как только при х > 0 выражение loga x имеем смысл.
б) Множество значений логарифмической функции представлено множеством R всех действительных чисел.
Это утверждение следует из того, что для любого числа b (b – действительное чсило) есть такое положительное число х, что loga x = b, т.е. уравнение loga x = b имеет корень. Такой корень существует; он равен х = аb, так как loga аb = b.
в) Логарифмическая функция у = loga x является возрастающей на промежутке х > 0, если а > 1, и убывающей, если 0 < а < 1.
Предположим, что а > 1. Докажем, что если х2 > х1 > 0, то у (х2) > у (х1), т.е. loga х2 > loga х1. Пользуясь основным логарифмическим тождеством, условие х2 > х1 можно записать так: а loga х2 >а loga х1. Из этого неравенства по свойству степени с основанием а > 1 следует, что loga х2 > loga х1.
Пусть 0 < а < 1. Докажем, что если х2 > х1 > 0, то loga х2 < loga х1.
Записав условие х2 > х1 в виде а loga х2 > а loga х1, получим loga х2 < loga х1, так как 0 < а < 1.
г) Если а > 1, то при х > 1 функция у = loga x принимает положительные значения, а при при 0 < х < 1 – отрицательные. Если 0 < а < 1, то функция у = loga x принимает положительные значения при 0 < х < 1, отрицательные – при х > 1.
Это следует из того, что функция у = loga x принимает значение, равное нулю, при х = 1 и является возрастающей на промежутке х > 0, если а > 0, и убывающей, если 0 < а < 1.
Отметим, что график любой логарифмической функции у = loga x проходит через точку (1; 0).
5) тригонометрические ф-ции y = sin x, y = cos x? y = tg x, y = ctg x
характеристики и свойства этих функций:
- область определения: - < x < +; область значений: -1 y +1;
- эти функции периодические: их период 2;
- функции ограниченные (| y | 1), всюду непрерывные, не монотонные, но имеющие так называемые интервалы монотонности, внутри которых они ведут себя, как монотонные функции;
- функции имеют бесчисленное множество нулей.
6) обратнотригоном ф-ции у=Arcsin x, у=Arccos x, y = Arctan x, y = Arccot x
Элементарной функцией называется функция, которая может быть задана одной формулой вида y=f(x), где справа стоящее выражение составлено из основных элементарных функций и постоянных при помощи конечного числа операций сложения, вычитания, умножения, деления и взятия функции от функции.
3. Элементы поведения функции. Монотонность. Четность и нечетность. Периодичность. Ограниченность и неограниченность. Привести примеры.
Монотонность. Определение: ф-ция y=f(x) называется возрастающей на некотором интервале, если на этом интервале большему значению x соответствует большее значение ф-ции, т. е. при x1<x2 имеет место неравенство f(x1)<f(x2). Рис3 Определение: ф-ция y=f(x) называется убывающей на некотором интервале, если на этом интервале большему значению x соответствует меньшее значение ф-ции, т. е. при x1<x2 имеет место неравенство f(x1)>f(x2).
Функ-ия возраст-щая или убыв-щая на множ-ве, назыв-ся монотонной ф-цией.
Прим.
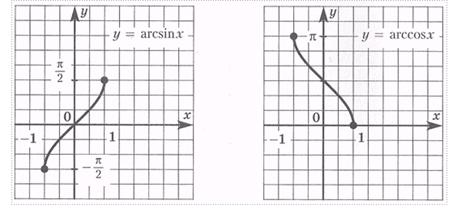
Чётность и нечётность.
Определение: ф-ция y=f(x) называется чётной, если для всех x из области определения f(-x)=f(x).
График чётной ф-ции симметричен относительно оси Oy.
Прим.
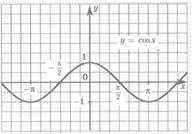
Определение: ф-ция y=f(x) называется нечётной, если для всех x из области определения f(-x)=-f(x). График чётной ф-ции симметричен относительно начала координат.
Прим.
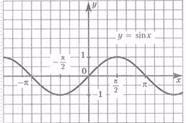
Если ни одно из вышеуказанных условий не выполняется, т. е. f(-x)¹f(x) и f(-x)¹-f(x), то ф-ция y=f(x) называется ф-цией общего вида.
Периодичность. Определение: ф-ция y=f(x) называется периодической с периодом T¹0, если для любых x из области определения справедливо равенство f(x+T) = f(x). Примечание: если число T есть период ф-ции y=f(x) заданной на всей числовой прямой, то число nT, nÎZ также является периодом ф-ции. В этом случае наименьший положительный период, если он существует, называется основным периодом ф-ции. Говоря о периоде ф-ции обычно имеют в виду наименьший положительный период.
Прим.
Ф-ции sin x, cos x (см. рис. выше) периодичные с периодом Т=2 π
Ограниченность. Ф-ция y=f(x) называется ограниченной на некотором промежутке, или существует такое положительное число M>0, что |f(x)|£M, для любого xÎX. Если ф-ция ограничена на некотором промежутке, то график этой ф-ции в пределах этого интервала расположен в полосе ограниченной прямыми y=a и y=b.
Прим. ф-ци ограниченные: sin x, cos x ограничены по оси У [-1,1]
Прим. ф-ци неограниченные: tg x
4. Определение числовой последовательности. Геометрическое изображение. Последовательности. Монотонные, ограниченные и неограниченные последовательности. Предел числовой последовательности. Геометрическая иллюстрация предела числовой последовательности. Теорема о единственности предела последовательности. Доказать теорему об ограниченности последовательности, имеющей предел.
Если каждому натур числу n по некоторому Закону поставлено в соответствие действ число Un? то говорят что задана ф-ция натур-го арг-та или числовая последовательность.
Предел функции в точке.
Пусть функция f(x) определена в некоторой окрестности точки х = а (т.е. в самой точке х = а функция может быть и не определена)
Определение. Число А называется пределом функции f(x) при х®а, если для любого e > 0 существует такое число D>0, что для всех х таких, что 0 < ïx - aï < D верно неравенствоïf(x) - Aï< e.
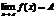 То же определение может быть записано в другом виде: если а - D < x < a + D, x ¹ a, то верно неравенство А - e < f(x) < A + e.Запись предела функции в точке:
То же определение может быть записано в другом виде: если а - D < x < a + D, x ¹ a, то верно неравенство А - e < f(x) < A + e.Запись предела функции в точке:
Геометрическая иллюстрация
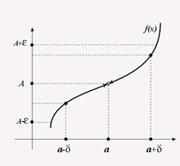
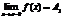
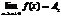 Определение. Если f(x) ® A1 при х ® а только при x < a, то называется пределом функции f(x) в точке х = а слева, а если f(x) ® A2 при х ® а только при x > a, то называется пределом функции f(x) в точке х = а справа. Приведенное выше определение относится к случаю, когда функция f(x) не определена в самой точке х = а, но определена в некоторой сколь угодно малой окрестности этой точки. Пределы А1 и А2 называются также односторонними пределами функции f(x) в точке х = а. Также говорят, что А – конечный предел функции f(x).
Определение. Если f(x) ® A1 при х ® а только при x < a, то называется пределом функции f(x) в точке х = а слева, а если f(x) ® A2 при х ® а только при x > a, то называется пределом функции f(x) в точке х = а справа. Приведенное выше определение относится к случаю, когда функция f(x) не определена в самой точке х = а, но определена в некоторой сколь угодно малой окрестности этой точки. Пределы А1 и А2 называются также односторонними пределами функции f(x) в точке х = а. Также говорят, что А – конечный предел функции f(x).
Предел функции при стремлении аргумента к бесконечности.
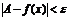 Определение. Число А называется пределом функции f(x) при х®¥, если для любого числа e>0 существует такое число М>0, что для всех х, ïхï>M выполняется неравенство При этом предполагается, что функция f(x) определена в окрестности бесконечности. Записывают:
Определение. Число А называется пределом функции f(x) при х®¥, если для любого числа e>0 существует такое число М>0, что для всех х, ïхï>M выполняется неравенство При этом предполагается, что функция f(x) определена в окрестности бесконечности. Записывают:
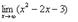
Прим.
6. Бесконечно большие функции при х®а и при х®¥. Геометрическая иллюстрация. Функция, ограниченная на интервале и в точке. Доказать теорему о связи функции, имеющей предел при х®а.
Бесконечно большие функции
Ф-ция f(x) опред в некотор окрестн точки х=а назыв бесконечно большой при х®а, если для любого числа М>0 существует такое число D>0, что неравенствоïf(x)ï>M выполняется при всех х, удовлетворяющих условию 0 < ïx - aï < D
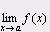
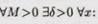
(0<|x-a|< D =>ïf(x)ï>M)
Определение. Ф-ция f(x) назыв бесконечно большой при х®∞, если для любого числа М>0 существует такое число K>0, что для всех |х|>K, выполняется неравенствоïf(x)ï>M
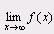
K>0, (|x|>K =>ïf(x)ï>M)
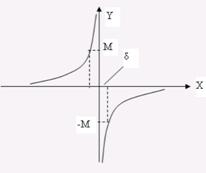
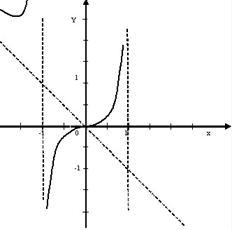
Классификация т-ки разрыва
Все т-ки р-рыва делятся на 3 вида: т. устранимого р-рыва; точки р-рыва 1-го, и 2-го рода.
а) если в т-ке х0 $ оба односторонних предела, которые совпадают между собой f(x0+)= f(x0-), но ¹ f(x0), то такая т-ка наз-ся точкой устранимого р-рыва.
Если х0 т-ка устранимого р-рыва, то можно перераспределить ф-цию f так чтобы она стала непр. в т-ке х0. Если по ф-ции f построить новую ф-цию положив для нее знач. f(x0)= f(x0-)=f(x0+) и сохранить знач. в др. т-ках, то получим исправл. f.
б) если в т-ке х0 $ оба 1-стороних предела f(x0±), которые не равны между собой f(x0+)¹f(x0-), то х0 наз-ся т-кой р-рыва первого рода.
в) если в т-ке х0 хотя бы 1 из односторонних пределов ф-ции не $ или бесконечен, то х0 наз-ся т-кой р-рыва 2-го рода.
При исслед. Ф-ции на непр. классификации возможных т-к р-рыва нужно применять во внимание сл. замечания:
1) Все элементарные ф-ции непрер. во внутренних т-ках своих областей определения => при исл. элементарных ф-ций нужно обращать внимание на гранич. т-ки обл-ти опр-ния.
2) Если ф-ция задана кусочно, т.е. различными соотношениями на частях своей обл. опр., то подозрительными на разрыв явл. граничные т-ки частей обл-ти опр.
3) Св-ва непр. ф-ций. Многие св-ва непр. ф-ций легко понять опираясь на их геометр. св-ва:
график непр. ф-ции на пр-ке D представляет сплошную(без р-рывов) кривую на пл-тях и след-но может отображена без отрыва ручки от бумаги.
I) Ф-ция непр. в т-ке х0 обязательно ограничена в окрестностях этой т-ки.(св-во локал. огранич-ти)
Док-во использует опр-ние на языке e и d. Если f непр. в т-ке х0 то взяв любое e>0 можно найти d>0 ½f(x)-f(x0)½<e при ½х-х0½<d ~ f(x0)-e<f(x)<f(x0)+e в окрестности в т-ке х0.
II) Св-ва сохранения знака Если f(x) непр. в т-ке х0 и f(x0)¹0 то $ окрестность этой т-ки в которой ф-ция принимает тот же знак что и знак х0.
III) Теорема о промежуточных знач. ф-ции f(x) непр. на отрезке [a,b] и f(a)=A, f(b)=B причем A¹B => CÎ(A,B) $ cÎ(a,b):f(c)=C f(c)=f(c‘)=f(c‘‘).
IV) Теорема о прохожд. непр. ф-циичерез 0. Если f(x) непр. на отрезке (a,b) и принимает на концах этого отрезка значение разных знаков f(a) f(b), то $ т-ка сÎ(a,b).

16. Доказать первый замечательный предел. Привести примеры.
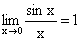 Обычно задачи на первый замечательный предел входят в стандартный перечень заданий типовых расчетов курса высшей математики. Разобраться в этом несложно, однако потребуются кое-какие знания из курса элементарной школьной тригонометрии. Начнем с определения.
Обычно задачи на первый замечательный предел входят в стандартный перечень заданий типовых расчетов курса высшей математики. Разобраться в этом несложно, однако потребуются кое-какие знания из курса элементарной школьной тригонометрии. Начнем с определения.
Первымзамечательным пределом именуют. Известны также и следствия из первого замечательного предела:
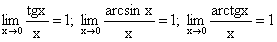
17. Доказать второй замечательный предел. Привести примеры. Натуральные логарифмы и их связь с десятичными логарифмами.
Второй замечательный предел имеет вид:

или в другой записи
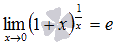
В случае второго замечательного предела имеем дело с неопределенностью вида единица в степени бесконечность 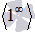 .
.
Разберем несколько примеров нахождения предела по второму замечательному пределу с подробным оприсанием решения.
Пример.
Вычислить предел 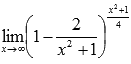
18. Сравнения бесконечно малых функций. Эквивалентные бесконечно малые функции. Основные эквивалентности. Привести примеры.


1.18. БМФ. lim(при xà∞) f(x)=0 – БМФ!
1] Две БМФ, при xà∞ f(x) и φ(x) называются бесконечно малыми одного порядка малости, если lim(при xà∞) f(x)/φ(x)=const.
2] БМФ f(x) при xà∞ называется бесконечно малой более высокого поярдка малости, чем БМФ φ(x) при xà∞, если предел lim(xà∞) f(x)/φ(x)=∞.
3] БМФ f(x) при xà∞ называется БМФ более низкого порядка малости, чем БМФ φ(x) при xà∞, если предел lim(xà∞) f(x)/φ(x)=∞.
4] Две БМФ при xà∞ называются несравнимыми, если придела lim(при xà∞) f(x)/φ(x) не существует.
5] Две БМФ называются эквивалентными при xà∞, если lim(при xà∞) f(x)/φ(x)=1;
ТЕОРЕМА 1: Если БМФ f(x)~f1(x) при xà∞, а БМФ φ(x)~φ1(x), при xà∞ и если существует lim f1(x)/φ1(x), то существует предел отношения: lim(при xà∞) f(x)/φ(x) = lim(при xà∞) f1(x)/φ1(x). Дано: f~f1=> lim(при xà∞) f(x)/f1(x)=1; φ(x)~φ1(x) => lim(при xà∞) φ(x)/φ1(x) => lim(при xà∞) φ(x)/φ1(x)=1; из всего этого => lim f1(x)/φ1(x) – существует. Док-ть: существует lim(при xà∞) f(x)/φ(x)=lim(при xà∞) f1(x)/φ1(x). Док-во: lim(при xà∞) f(x)/φ(x)=lim(при xà) f(x) f1(x) φ1(x)/ φ(x) f1(x) φ1(x)= =lim(при xà∞) f(x)/f1(x) *1/φ(x)/φ1(x) * f1(x)/φ1(x)=lim(при xà∞) f1(x)/φ1(x).
ТЕОРЕМА 2: Сумма БМФ эквивалентна бесконечно малой низшего порядка. Дано: f(x)+φ(x)+g(x)àБМФ при xà∞; lim(xà∞) φ(x)/f(x)=0, lim(xà∞) g(x)/f(x)=0; Док-ть: f(x)+φ(x)+g(x)~f(x)-??? Док-во: lim(xà∞) (f(x)+φ(x)+g(x))/f(x)=lim(xà∞)1 + lim(xà∞) φ(x)/f(x) + lim(xà∞) g(x)/f(x).
19. Свойства эквивалентных бесконечно малых функций.
1) a ~ a, 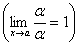
2) Если a ~ b и b ~ g, то a ~ g, 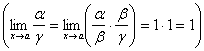
3) Если a ~ b, то b ~ a, 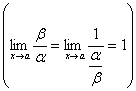
4) Если a ~ a1 и b ~ b1 и 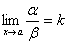 , то и
, то и 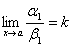 или
или 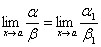 .
.
Следствие: а) если a ~ a1 и 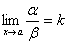 , то и
, то и 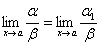
б) если b ~ b1 и 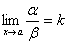 , то
, то 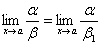
Свойство 4 особенно важно на практике, т.к. оно фактически означает, что предел отношения бесконечно малых не меняется при замене их на эквивалентные бесконечно малые. Этот факт дает возможность при нахождении пределов заменять бесконечно малые на эквивалентные им функции, что может сильно упростить вычисление пределов.
[an error occurred while processing this directive]
Пример. Найти предел 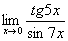
Так как tg5x ~ 5x и sin7x ~ 7x при х ® 0, то, заменив функции эквивалентными бесконечно малыми, получим:
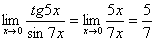
1. Задачи, приводящие к понятию производной. Производная как скорость изменения функции. Привести примеры. Геометрический смысл производной. Уравнения касательной и нормали к кривой.

Теорема Ферма.
Если f(x) дифф. в точке x0 и принимает в хтой точке наибольш. или наименьш. значение для некоторой окресности точки x0, то f’(x)=0. Доказательство: 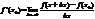 пусть f(x0) – наибольшая
пусть f(x0) – наибольшая
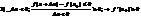
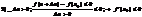
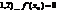
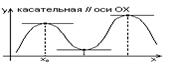
2. Теорема Роля. Геометрический смысл.
Точки экстремума.
Определение. Функция f(x) имеет в точке х1 максимум, если ее значение в этой точке больше значений во всех точках некоторого интервала, содержащего точку х1. Функция f(x) имеет в точке х2 минимум, если f(x2 +Dx) > f(x2) при любом Dх (Dх может быть и отрицательным).Очевидно, что функция, определенная на отрезке может иметь максимум и минимум только в точках, находящихся внутри этого отрезка. Нельзя также путать максимум и минимум функции с ее наибольшим и наименьшим значением на отрезке – это понятия принципиально различные. Определение. Точки максимума и минимума функции называются точками экстремума. Теорема. (необходимое условие существования экстремума) Если функция f(x) дифференцируема в точке х = х1 и точка х1 является точкой экстремума, то производная функции обращается в нуль в этой точке. Доказательство. Предположим, что функция f(x) имеет в точке х = х1 максимум. Тогда при достаточно малых положительных Dх>0 верно неравенство: 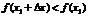 , т.е.
, т.е. 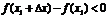 Тогда
Тогда 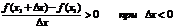
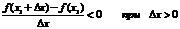 По определению:
По определению: 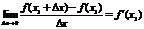 Т.е. если Dх®0, но Dх<0, то f¢(x1) ³ 0, а если Dх®0, но Dх>0, то f¢(x1) £ 0.А возможно это только в том случае, если при Dх®0 f¢(x1) = 0. Для случая, если функция f(x) имеет в точке х2 минимум теорема доказывается аналогично. Следствие. Обратное утверждение неверно. Если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум. Красноречивый пример этого – функция у = х3, производная которой в точке х = 0 равна нулю, однако в этой точке функция имеет только перегиб, а не максимум или минимум. Определение. Критическими точками функции называются точки, в которых производная функции не существует или равна нулю. Рассмотренная выше теорема дает нам необходимые условия существования экстремума, но этого недостаточно. Пример: f(x) = ôxô рис1 Пример: f(x) =
Т.е. если Dх®0, но Dх<0, то f¢(x1) ³ 0, а если Dх®0, но Dх>0, то f¢(x1) £ 0.А возможно это только в том случае, если при Dх®0 f¢(x1) = 0. Для случая, если функция f(x) имеет в точке х2 минимум теорема доказывается аналогично. Следствие. Обратное утверждение неверно. Если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум. Красноречивый пример этого – функция у = х3, производная которой в точке х = 0 равна нулю, однако в этой точке функция имеет только перегиб, а не максимум или минимум. Определение. Критическими точками функции называются точки, в которых производная функции не существует или равна нулю. Рассмотренная выше теорема дает нам необходимые условия существования экстремума, но этого недостаточно. Пример: f(x) = ôxô рис1 Пример: f(x) = 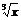 рис2 В точке х = 0 функция имеет минимум, но не имеет производной. В точке х = 0 функция не имеет ни максимума, ни минимума, ни производной.
рис2 В точке х = 0 функция имеет минимум, но не имеет производной. В точке х = 0 функция не имеет ни максимума, ни минимума, ни производной.
Вообще говоря, функция f(x) может иметь экстремум в точках, где производная не существует или равна нулю. Теорема. (Достаточные условия существования экстремума) Пусть функция f(x) непрерывна в интервале (a, b), который содержит критическую точку х1, и дифференцируема во всех точках этого интервала (кроме, может быть, самой точки х1). Если при переходе через точку х1 слева направо производная функции f¢(x) меняет знак с “+” на “-“, то в точке х = х1 функция f(x) имеет максимум, а если производная меняет знак с “-“ на “+”- то функция имеет минимум.
Доказательство. Пусть 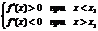 По теореме Лагранжа: f(x) – f(x1) = f¢(e)(x – x1), где x < e < x1. Тогда: 1) Если х < x1, то e < x1; f¢(e)>0; f¢(e)(x – x1)<0, следовательно f(x) – f(x1)<0 или f(x) < f(x1). 2) Если х > x1, то e > x1 f¢(e)<0; f¢(e)(x – x1)<0, следовательно f(x) – f(x1)<0 или f(x) < f(x1). Т. к. ответы совпадают, то можно сказать, что f(x) < f(x1) в любых точках вблизи х1, т.е. х1 – точка максимума.
По теореме Лагранжа: f(x) – f(x1) = f¢(e)(x – x1), где x < e < x1. Тогда: 1) Если х < x1, то e < x1; f¢(e)>0; f¢(e)(x – x1)<0, следовательно f(x) – f(x1)<0 или f(x) < f(x1). 2) Если х > x1, то e > x1 f¢(e)<0; f¢(e)(x – x1)<0, следовательно f(x) – f(x1)<0 или f(x) < f(x1). Т. к. ответы совпадают, то можно сказать, что f(x) < f(x1) в любых точках вблизи х1, т.е. х1 – точка максимума.
4. Доказать 1-ый достаточный признак точек экстремума.

5. Доказать 2-ой достаточный признак точек экстремума.

6. Определение выпуклости и вогнутости графика функции на интервале. Доказать достаточные условия выпуклости и вогнутости.
Точкой перегиба
Определение. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба. Очевидно, что в точке перегиба касательная пересекает кривую. Теорема 2. Пусть кривая определяется уравнением y = f(x). Если вторая производная f¢¢(a) = 0 или f¢¢(a) не существует и при переходе через точку х = а f¢¢(x) меняет знак, то точка кривой с абсциссой х = а является точкой перегиба.
Доказательство. 1) Пусть f¢¢(x) < 0 при х < a и f¢¢(x) > 0 при x > a. Тогда при x < a кривая выпукла, а при x > a кривая вогнута, т.е. точка х = а – точка перегиба. Пусть f¢¢(x) > 0 при x < b и f¢¢(x) < 0 при x < b. Тогда при x < b кривая обращена выпуклостью вниз, а при x > b – выпуклостью вверх. Тогда x = b – точка перегиба.
8. Асимптоты графика функции. Наклонные асимптоты. Вертикальные асимптоты. Привести примеры
Асимптоты.
При исследовании функций часто бывает, что при удалении координаты х точки кривой в бесконечность кривая неограниченно приближается к некоторой прямой. Определение. Прямая называется асимптотой кривой, если расстояние от переменной точки кривой до этой прямой при удалении точки в бесконечность стремится к нулю. Следует отметить, что не любая кривая имеет асимптоту. Асимптоты могут быть прямые и наклонные. Исследование функций на наличие асимптот имеет большое значение и позволяет более точно определить характер функции и поведение графика кривой. Вообще говоря, кривая, неограниченно приближаясь к своей асимптоте, может и пересекать ее, причем не в одной точке, как показано на приведенном ниже графике функции 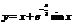 . Ее наклонная асимптота у = х. Рис 1 Рассмотрим подробнее методы нахождения асимптот кривых. Вертикальные асимптоты. Из определения асимптоты следует, что если предел или один из односторонних пределов раны бесконечности, то прямая х = а – асимптота кривой y = f(x). Например, для функции
. Ее наклонная асимптота у = х. Рис 1 Рассмотрим подробнее методы нахождения асимптот кривых. Вертикальные асимптоты. Из определения асимптоты следует, что если предел или один из односторонних пределов раны бесконечности, то прямая х = а – асимптота кривой y = f(x). Например, для функции 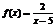 прямая х = 5 является вертикальной асимптотой. Наклонные асимптоты. Предположим, что кривая y = f(x) имеет наклонную асимптоту y = kx + b. Рис 2Обозначим точку пересечения кривой и перпендикуляра к асимптоте – М, Р – точка пересечения этого перпендикуляра с асимптотой. Угол между асимптотой и осью Ох обозначим j. Перпендикуляр МQ к оси Ох пересекает асимптоту в точке N. Тогда MQ = y – ордината точки кривой, NQ =
прямая х = 5 является вертикальной асимптотой. Наклонные асимптоты. Предположим, что кривая y = f(x) имеет наклонную асимптоту y = kx + b. Рис 2Обозначим точку пересечения кривой и перпендикуляра к асимптоте – М, Р – точка пересечения этого перпендикуляра с асимптотой. Угол между асимптотой и осью Ох обозначим j. Перпендикуляр МQ к оси Ох пересекает асимптоту в точке N. Тогда MQ = y – ордината точки кривой, NQ = 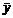 - ордината точки N на асимптоте.
- ордината точки N на асимптоте.
1. Определение первообразной. График первообразной. Определение неопределенного интеграла. Теорема существования неопределенного интеграла (без док-ва). Свойства неопределенного интеграла.
Интегрирование по частям.
Способ основан на известной формуле производной произведения:
(uv)¢ = u¢v + v¢uгде u и v – некоторые функции от х. В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав, получаем: 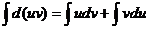 , а в соответствии с приведенными выше свойствами неопределенного интеграла:
, а в соответствии с приведенными выше свойствами неопределенного интеграла: 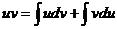 или
или 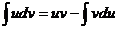 ; Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
; Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
Пример. 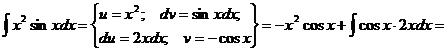
Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.
Пример. 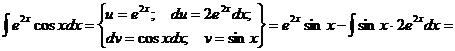
4. Интегрирование подстановкой. Тригонометрические подстановки. Привести примеры.
Определенный интеграл.
Пусть на отрезке [a, b] задана непрерывная функция f(x). Рис 1. Обозначим m и M наименьшее и наибольшее значение функции на отрезке [a, b] Разобьем отрезок [a, b] на части (не обязательно одинаковые) n точками. x0 < x1 < x2 < … < xn Тогда x1 – x0 = Dx1, x2 – x1 = Dx2, …,xn – xn-1 = Dxn; На каждом из полученных отрезков найдем наименьшее и наибольшее значение функции. [x0, x1] ® m1, M1; [x1, x2] ® m2, M2; … [xn-1, xn] ® mn, Mn. Составим суммы: 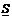 (далее_4_)n = m1Dx1 + m2Dx2 + … +mnDxn =
(далее_4_)n = m1Dx1 + m2Dx2 + … +mnDxn = 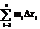
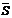 (_2_n)= M1Dx1 + M2Dx2 + … + MnDxn =
(_2_n)= M1Dx1 + M2Dx2 + … + MnDxn = 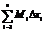 Сумма _4_ называется нижней интегральной суммой, а сумма _2_ – верхней интегральной суммой. Т.к. mi £ Mi, то _4_n £ _2_n, а m(b – a) £ _4_n £ _2_n £ M(b – a)Внутри каждого отрезка выберем некоторую точку e. x0 < e1 < x1, x1 < e < x2, …, xn-1 < e < xn.Найдем значения функции в этих точках и составим выражение, которое называется интегральной суммой для функции f(x) на отрезке [a, b]. Sn = f(e1)Dx1 + f(e2)Dx2 + … + f(en)Dxn =
Сумма _4_ называется нижней интегральной суммой, а сумма _2_ – верхней интегральной суммой. Т.к. mi £ Mi, то _4_n £ _2_n, а m(b – a) £ _4_n £ _2_n £ M(b – a)Внутри каждого отрезка выберем некоторую точку e. x0 < e1 < x1, x1 < e < x2, …, xn-1 < e < xn.Найдем значения функции в этих точках и составим выражение, которое называется интегральной суммой для функции f(x) на отрезке [a, b]. Sn = f(e1)Dx1 + f(e2)Dx2 + … + f(en)Dxn = 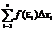 Тогда можно записать: miDxi £ f(ei)Dxi £ MiDxi Следовательно,
Тогда можно записать: miDxi £ f(ei)Dxi £ MiDxi Следовательно, 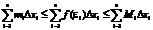
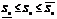 Геометрически это представляется следующим образом: график функции f(x) ограничен сверху описанной ломаной линией, а снизу – вписанной ломаной. Обозначим maxDxi – наибольший отрезок разбиения, а minDxi – наименьший. Если maxDxi® 0, то число отрезков разбиения отрезка [a, b] стремится к бесконечности. Если
Геометрически это представляется следующим образом: график функции f(x) ограничен сверху описанной ломаной линией, а снизу – вписанной ломаной. Обозначим maxDxi – наибольший отрезок разбиения, а minDxi – наименьший. Если maxDxi® 0, то число отрезков разбиения отрезка [a, b] стремится к бесконечности. Если 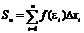 (8), то
(8), то 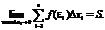 (_9_) Определение: Если при любых разбиениях отрезка [a, b] таких, что maxDxi® 0 и произвольном выборе точек ei интегральная сумма _8_ стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b]. Обозначение:
(_9_) Определение: Если при любых разбиениях отрезка [a, b] таких, что maxDxi® 0 и произвольном выборе точек ei интегральная сумма _8_ стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b]. Обозначение: 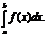 (_10_) а – нижний предел, b – верхний предел, х – переменная интегрирования, [a, b] – отрезок интегрирования. Определение: Если для функции f(x) существует предел _9_=_10_ то функция называется интегрируемой на отрезке [a, b]. Теорема: Если функция f(x) непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.
(_10_) а – нижний предел, b – верхний предел, х – переменная интегрирования, [a, b] – отрезок интегрирования. Определение: Если для функции f(x) существует предел _9_=_10_ то функция называется интегрируемой на отрезке [a, b]. Теорема: Если функция f(x) непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.
2. Свойства определенного интеграла, вытекающие из определения.
Свойство 1. Производная от определённого интеграла по верхнему пределу равна подынтегральной функции, в которую вместо переменной интегрирования подставлено значение верхнего предела. То есть
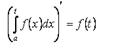
Свойство 2. Определённый интеграл от суммы функций равен сумме неопределённых интегралов
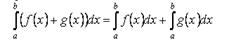
Свойство 3. Постоянный множитель можно выносить за знак определённого интеграла
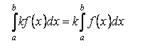
Свойство 4. Если на отрезке [a,b], где a < b, функции f(x) и g(x) удовлетворяют условию f(x) ≤ g(x), то

Свойство 5. Если m и M - наименьшее и наибольшее значения функции f(x) на отрезке [a,b] и a ≤ b, то
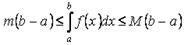
Свойство 6. Если поменять местами верхний и нижний пределы интегрирования, то определённый интеграл изменит знак
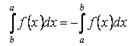
Свойство 7. Для любых трёх чисел a, b, c справедливо равенство
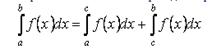
если только все три интеграла существуют.
Свойство 8 (Теорема о среднем). Если функция f(x) непрерывна на отрезке [a,b], то на этом отрезке найдётся такая точка c, что справедливо равенство:
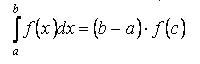
3. Теорема об оценке определенного интеграла. Теорема о среднем. Геометрический смысл.
Теоремы об оценке интеграла.
5.1. Если на отрезке [a,b] функция удовлетворяет неравенству m≤f(x)≤M, то
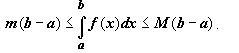
Док-во. Докажем левое неравенство (цифрами над знаками импликации обозначены номера применяемых ранее доказанных свойств):
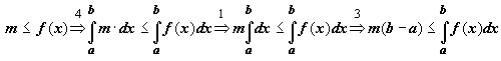
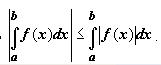 Аналогично доказывается и правое неравенство.
Аналогично доказывается и правое неравенство.
5.2. Если функция f(x) интегрируема по отрезку [a,b], то
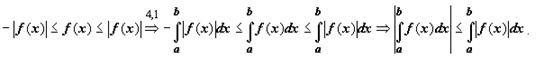
Док-во.
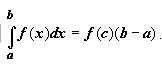
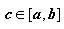 6. Теорема о среднем.
6. Теорема о среднем.
Если f(x) непрерывна на отрезке [a,b], то существует точка, такая что
Док-во. Функция, непрерывная на отрезке, принимает на этом отрезке своё наименьшее m и наибольшее M значения. Тогда
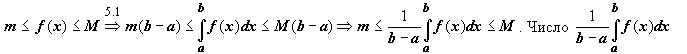
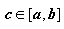 заключено между минимальным и максимальным значениями функции на отрезке. Одно из свойств функции, непрерывной на отрезке, заключается в том, что эта функция принимает любое значение, расположенное между m и M. Таким образом, существует точка, такая что
заключено между минимальным и максимальным значениями функции на отрезке. Одно из свойств функции, непрерывной на отрезке, заключается в том, что эта функция принимает любое значение, расположенное между m и M. Таким образом, существует точка, такая что
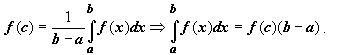
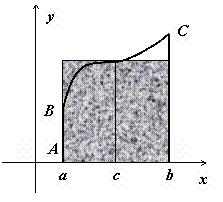 Это свойство имеет простую геометрическую интерпретацию: если f(x) ≥ 0 непрерывна на отрезке [a,b], то существует точка такая, что площадь криволинейной трапеции ABCD равна площади прямоугольника с основанием [a,b] и высотой f(c) (на рисунке выделен цветом).
Это свойство имеет простую геометрическую интерпретацию: если f(x) ≥ 0 непрерывна на отрезке [a,b], то существует точка такая, что площадь криволинейной трапеции ABCD равна площади прямоугольника с основанием [a,b] и высотой f(c) (на рисунке выделен цветом).
Геометрический смысл доказанных неравенств таков: площадь криволинейной трапеции больше площади прямоугольника с основанием, равным основанию трапеции, и высотой, равной наименьшей ординате трапеции, и меньше площади прямоугольника с тем же основанием и высотой, равной наибольшей ординате трапеции (рис. 1).
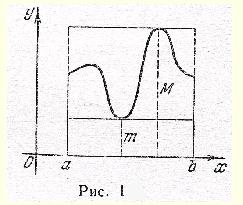 Находя границы для интеграла, мы, как говорят, производим его оценку. Может случиться, что весьма трудно или даже невозможно найти точное значение интеграла, а оценивая его, мы узнаем, хотя бы грубо, приближенное его значение. С такого рода оценками приходится довольно часто встречаться в математике.
Находя границы для интеграла, мы, как говорят, производим его оценку. Может случиться, что весьма трудно или даже невозможно найти точное значение интеграла, а оценивая его, мы узнаем, хотя бы грубо, приближенное его значение. С такого рода оценками приходится довольно часто встречаться в математике.
Указанные в теореме об оценке определенного интеграла границы для интеграла тем более точны, чем короче интервал интегрирования и чем меньше линия y=f(x) отличается по положению от прямой, параллельной оси Ox.
4. Определенный интеграл с переменным верхним пределом. Производная от определенного интеграла с переменным верхним пределом. Связь определенного интеграла с неопределенным. Формула Ньютона-Лейбница.
Вычисление площадей плоских фигур. Рис 1
Известно, что определенный интеграл на отрезке представляет собой площадь криволинейной трапеции, ограниченной графиком функции f(x). Если график расположен ниже оси Ох, т.е. f(x) < 0, то площадь имеет знак “-“, если график расположен выше оси Ох, т.е. f(x) > 0, то площадь имеет знак “+”.
Для нахождения суммарной площади используется формула 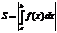 .
.
Площадь фигуры, ограниченной некоторыми линиями может быть найдена с помощью определенных интегралов, если известны уравнения этих линий.
Пример. Найти площадь фигуры, ограниченной линиями y = x, y = x2, x = 2. Рис 2.
Искомая площадь (заштрихована на рисунке) может быть найдена по формуле:
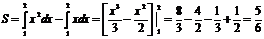 (ед2)
(ед2)
10. Вычисление объектов тел с помощью определенного интеграла по площадям поперечных сечений. Объем тел вращения. Привести примеры.
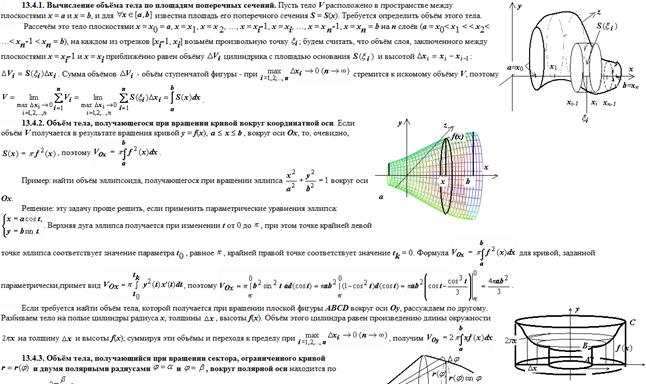
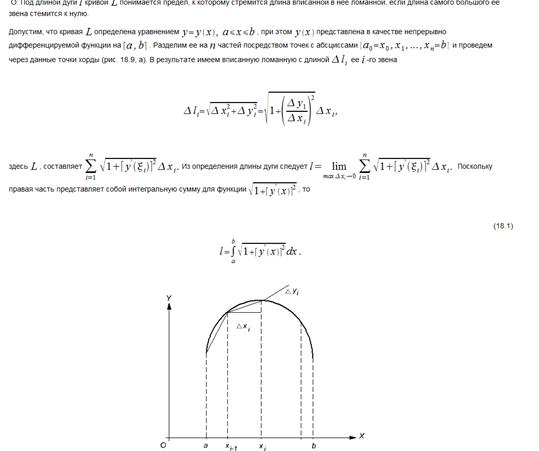
11. Вычисление длин дуг кривой с помощью определенного интеграла. Привести примеры.
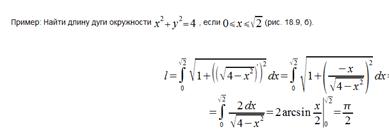
Классификация ф-ций.

Функции заданные единой формулой классифицируются в зависимости от характера алгебр-х действий, кот. надо совершить над арг. что бы получить знач. ф-ции.
- Целорацион-ый многочлен (полином), если прим операции слож, умнож, возв в целую степень.
Прим. у=х3+3х²-5х
- Если к операц 1 добавит деление, то получ класс рацион ф-ций.
Прим. у=х4-3х²+1/(х-3)
-
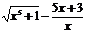 Е сли к перечисл опер доб извл корня то получ класс алгебр-х ф-ций
Е сли к перечисл опер доб извл корня то получ класс алгебр-х ф-ций
Прим.
Основные элементарные функции.
Основными элементарными функциями называются следующие: степенная, показательная, логарифмическая, тригонометрические, обратные тригонометрические (arcsin..) (поподробнее расписать с примерами и графиками).
1) у=const
2) у=хn, n? R – степенные ф-ции

3) у=ах, а>0, а≠1 – показательные ф-ции

4) у=logах, а>0, а≠1 – логарифмические ф-ции
а) Областью определения логарифмической функции является множество всех положительных чисел.
Это утверждение следует из определения логарифма, так как только при х > 0 выражение loga x имеем смысл.
б) Множество значений логарифмической функции представлено множеством R всех действительных чисел.
Это утверждение следует из того, что для любого числа b (b – действительное чсило) есть такое положительное число х, что loga x = b, т.е. уравнение loga x = b имеет корень. Такой корень существует; он равен х = аb, так как loga аb = b.
в) Логарифмическая функция у = loga x является возрастающей на промежутке х > 0, если а > 1, и убывающей, если 0 < а < 1.
Предположим, что а > 1. Докажем, что если х2 > х1 > 0, то у (х2) > у (х1), т.е. loga х2 > loga х1. Пользуясь основным логарифмическим тождеством, условие х2 > х1 можно записать так: а loga х2 >а loga х1. Из этого неравенства по свойству степени с основанием а > 1 следует, что loga х2 > loga х1.
Пусть 0 < а < 1. Докажем, что если х2 > х1 > 0, то loga х2 < loga х1.
Записав условие х2 > х1 в виде а loga х2 > а loga х1, получим loga х2 < loga х1, так как 0 < а < 1.
г) Если а > 1, то при х > 1 функция у = loga x принимает положительные значения, а при при 0 < х < 1 – отрицательные. Если 0 < а < 1, то функция у = loga x принимает положительные значения при 0 < х < 1, отрицательные – при х > 1.
Это следует из того, что функция у = loga x принимает значение,




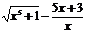 Е сли к перечисл опер доб извл корня то получ класс алгебр-х ф-ций
Е сли к перечисл опер доб извл корня то получ класс алгебр-х ф-ций




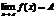 То же определение может быть записано в другом виде: если а - D < x < a + D, x ¹ a, то верно неравенство А - e < f(x) < A + e.Запись предела функции в точке:
То же определение может быть записано в другом виде: если а - D < x < a + D, x ¹ a, то верно неравенство А - e < f(x) < A + e.Запись предела функции в точке:
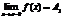
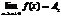 Определение. Если f(x) ® A1 при х ® а только при x < a, то называется пределом функции f(x) в точке х = а слева, а если f(x) ® A2 при х ® а только при x > a, то называется пределом функции f(x) в точке х = а справа. Приведенное выше определение относится к случаю, когда функция f(x) не определена в самой точке х = а, но определена в некоторой сколь угодно малой окрестности этой точки. Пределы А1 и А2 называются также односторонними пределами функции f(x) в точке х = а. Также говорят, что А – конечный предел функции f(x).
Определение. Если f(x) ® A1 при х ® а только при x < a, то называется пределом функции f(x) в точке х = а слева, а если f(x) ® A2 при х ® а только при x > a, то называется пределом функции f(x) в точке х = а справа. Приведенное выше определение относится к случаю, когда функция f(x) не определена в самой точке х = а, но определена в некоторой сколь угодно малой окрестности этой точки. Пределы А1 и А2 называются также односторонними пределами функции f(x) в точке х = а. Также говорят, что А – конечный предел функции f(x).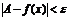 Определение. Число А называется пределом функции f(x) при х®¥, если для любого числа e>0 существует такое число М>0, что для всех х, ïхï>M выполняется неравенство При этом предполагается, что функция f(x) определена в окрестности бесконечности. Записывают:
Определение. Число А называется пределом функции f(x) при х®¥, если для любого числа e>0 существует такое число М>0, что для всех х, ïхï>M выполняется неравенство При этом предполагается, что функция f(x) определена в окрестности бесконечности. Записывают: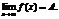
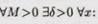
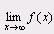
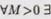
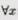



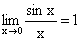 Обычно задачи на первый замечательный предел входят в стандартный перечень заданий типовых расчетов курса высшей математики. Разобраться в этом несложно, однако потребуются кое-какие знания из курса элементарной школьной тригонометрии. Начнем с определения.
Обычно задачи на первый замечательный предел входят в стандартный перечень заданий типовых расчетов курса высшей математики. Разобраться в этом несложно, однако потребуются кое-какие знания из курса элементарной школьной тригонометрии. Начнем с определения.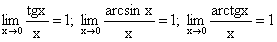

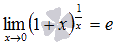
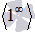 .
.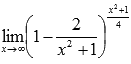


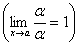
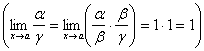
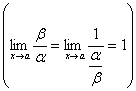
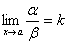 , то и
, то и 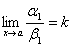 или
или 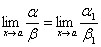 .
.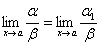
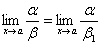
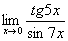
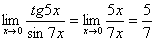

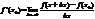 пусть f(x0) – наибольшая
пусть f(x0) – наибольшая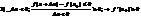
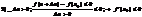
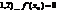

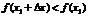 , т.е.
, т.е. 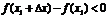 Тогда
Тогда 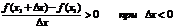
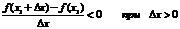 По определению:
По определению: 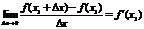 Т.е. если Dх®0, но Dх<0, то f¢(x1) ³ 0, а если Dх®0, но Dх>0, то f¢(x1) £ 0.А возможно это только в том случае, если при Dх®0 f¢(x1) = 0. Для случая, если функция f(x) имеет в точке х2 минимум теорема доказывается аналогично. Следствие. Обратное утверждение неверно. Если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум. Красноречивый пример этого – функция у = х3, производная которой в точке х = 0 равна нулю, однако в этой точке функция имеет только перегиб, а не максимум или минимум. Определение. Критическими точками функции называются точки, в которых производная функции не существует или равна нулю. Рассмотренная выше теорема дает нам необходимые условия существования экстремума, но этого недостаточно. Пример: f(x) = ôxô рис1 Пример: f(x) =
Т.е. если Dх®0, но Dх<0, то f¢(x1) ³ 0, а если Dх®0, но Dх>0, то f¢(x1) £ 0.А возможно это только в том случае, если при Dх®0 f¢(x1) = 0. Для случая, если функция f(x) имеет в точке х2 минимум теорема доказывается аналогично. Следствие. Обратное утверждение неверно. Если производная функции в некоторой точке равна нулю, то это еще не значит, что в этой точке функция имеет экстремум. Красноречивый пример этого – функция у = х3, производная которой в точке х = 0 равна нулю, однако в этой точке функция имеет только перегиб, а не максимум или минимум. Определение. Критическими точками функции называются точки, в которых производная функции не существует или равна нулю. Рассмотренная выше теорема дает нам необходимые условия существования экстремума, но этого недостаточно. Пример: f(x) = ôxô рис1 Пример: f(x) = 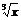 рис2 В точке х = 0 функция имеет минимум, но не имеет производной. В точке х = 0 функция не имеет ни максимума, ни минимума, ни производной.
рис2 В точке х = 0 функция имеет минимум, но не имеет производной. В точке х = 0 функция не имеет ни максимума, ни минимума, ни производной.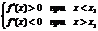 По теореме Лагранжа: f(x) – f(x1) = f¢(e)(x – x1), где x < e < x1. Тогда: 1) Если х < x1, то e < x1; f¢(e)>0; f¢(e)(x – x1)<0, следовательно f(x) – f(x1)<0 или f(x) < f(x1). 2) Если х > x1, то e > x1 f¢(e)<0; f¢(e)(x – x1)<0, следовательно f(x) – f(x1)<0 или f(x) < f(x1). Т. к. ответы совпадают, то можно сказать, что f(x) < f(x1) в любых точках вблизи х1, т.е. х1 – точка максимума.
По теореме Лагранжа: f(x) – f(x1) = f¢(e)(x – x1), где x < e < x1. Тогда: 1) Если х < x1, то e < x1; f¢(e)>0; f¢(e)(x – x1)<0, следовательно f(x) – f(x1)<0 или f(x) < f(x1). 2) Если х > x1, то e > x1 f¢(e)<0; f¢(e)(x – x1)<0, следовательно f(x) – f(x1)<0 или f(x) < f(x1). Т. к. ответы совпадают, то можно сказать, что f(x) < f(x1) в любых точках вблизи х1, т.е. х1 – точка максимума.

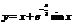 . Ее наклонная асимптота у = х. Рис 1 Рассмотрим подробнее методы нахождения асимптот кривых. Вертикальные асимптоты. Из определения асимптоты следует, что если предел или один из односторонних пределов раны бесконечности, то прямая х = а – асимптота кривой y = f(x). Например, для функции
. Ее наклонная асимптота у = х. Рис 1 Рассмотрим подробнее методы нахождения асимптот кривых. Вертикальные асимптоты. Из определения асимптоты следует, что если предел или один из односторонних пределов раны бесконечности, то прямая х = а – асимптота кривой y = f(x). Например, для функции 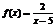 прямая х = 5 является вертикальной асимптотой. Наклонные асимптоты. Предположим, что кривая y = f(x) имеет наклонную асимптоту y = kx + b. Рис 2Обозначим точку пересечения кривой и перпендикуляра к асимптоте – М, Р – точка пересечения этого перпендикуляра с асимптотой. Угол между асимптотой и осью Ох обозначим j. Перпендикуляр МQ к оси Ох пересекает асимптоту в точке N. Тогда MQ = y – ордината точки кривой, NQ =
прямая х = 5 является вертикальной асимптотой. Наклонные асимптоты. Предположим, что кривая y = f(x) имеет наклонную асимптоту y = kx + b. Рис 2Обозначим точку пересечения кривой и перпендикуляра к асимптоте – М, Р – точка пересечения этого перпендикуляра с асимптотой. Угол между асимптотой и осью Ох обозначим j. Перпендикуляр МQ к оси Ох пересекает асимптоту в точке N. Тогда MQ = y – ордината точки кривой, NQ = 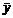 - ордината точки N на асимптоте.
- ордината точки N на асимптоте.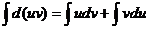 , а в соответствии с приведенными выше свойствами неопределенного интеграла:
, а в соответствии с приведенными выше свойствами неопределенного интеграла: 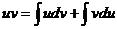 или
или 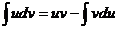 ; Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
; Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.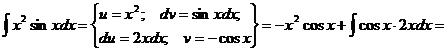
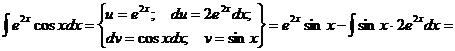
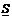 (далее_4_)n = m1Dx1 + m2Dx2 + … +mnDxn =
(далее_4_)n = m1Dx1 + m2Dx2 + … +mnDxn = 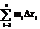
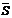 (_2_n)= M1Dx1 + M2Dx2 + … + MnDxn =
(_2_n)= M1Dx1 + M2Dx2 + … + MnDxn = 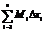 Сумма _4_ называется нижней интегральной суммой, а сумма _2_ – верхней интегральной суммой. Т.к. mi £ Mi, то _4_n £ _2_n, а m(b – a) £ _4_n £ _2_n £ M(b – a)Внутри каждого отрезка выберем некоторую точку e. x0 < e1 < x1, x1 < e < x2, …, xn-1 < e < xn.Найдем значения функции в этих точках и составим выражение, которое называется интегральной суммой для функции f(x) на отрезке [a, b]. Sn = f(e1)Dx1 + f(e2)Dx2 + … + f(en)Dxn =
Сумма _4_ называется нижней интегральной суммой, а сумма _2_ – верхней интегральной суммой. Т.к. mi £ Mi, то _4_n £ _2_n, а m(b – a) £ _4_n £ _2_n £ M(b – a)Внутри каждого отрезка выберем некоторую точку e. x0 < e1 < x1, x1 < e < x2, …, xn-1 < e < xn.Найдем значения функции в этих точках и составим выражение, которое называется интегральной суммой для функции f(x) на отрезке [a, b]. Sn = f(e1)Dx1 + f(e2)Dx2 + … + f(en)Dxn = 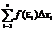 Тогда можно записать: miDxi £ f(ei)Dxi £ MiDxi Следовательно,
Тогда можно записать: miDxi £ f(ei)Dxi £ MiDxi Следовательно, 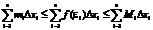
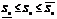 Геометрически это представляется следующим образом: график функции f(x) ограничен сверху описанной ломаной линией, а снизу – вписанной ломаной. Обозначим maxDxi – наибольший отрезок разбиения, а minDxi – наименьший. Если maxDxi® 0, то число отрезков разбиения отрезка [a, b] стремится к бесконечности. Если
Геометрически это представляется следующим образом: график функции f(x) ограничен сверху описанной ломаной линией, а снизу – вписанной ломаной. Обозначим maxDxi – наибольший отрезок разбиения, а minDxi – наименьший. Если maxDxi® 0, то число отрезков разбиения отрезка [a, b] стремится к бесконечности. Если 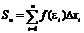 (8), то
(8), то 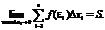 (_9_) Определение: Если при любых разбиениях отрезка [a, b] таких, что maxDxi® 0 и произвольном выборе точек ei интегральная сумма _8_ стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b]. Обозначение:
(_9_) Определение: Если при любых разбиениях отрезка [a, b] таких, что maxDxi® 0 и произвольном выборе точек ei интегральная сумма _8_ стремится к пределу S, который называется определенным интегралом от f(x) на отрезке [a, b]. Обозначение: 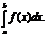 (_10_) а – нижний предел, b – верхний предел, х – переменная интегрирования, [a, b] – отрезок интегрирования. Определение: Если для функции f(x) существует предел _9_=_10_ то функция называется интегрируемой на отрезке [a, b]. Теорема: Если функция f(x) непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.
(_10_) а – нижний предел, b – верхний предел, х – переменная интегрирования, [a, b] – отрезок интегрирования. Определение: Если для функции f(x) существует предел _9_=_10_ то функция называется интегрируемой на отрезке [a, b]. Теорема: Если функция f(x) непрерывна на отрезке [a, b], то она интегрируема на этом отрезке.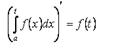
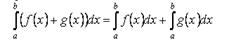
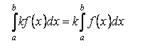

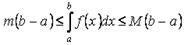
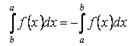
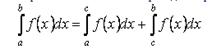
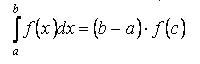
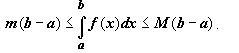
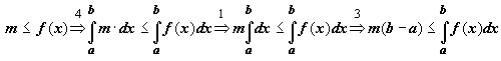
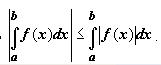 Аналогично доказывается и правое неравенство.
Аналогично доказывается и правое неравенство.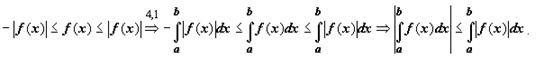
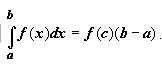
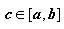 6. Теорема о среднем.
6. Теорема о среднем.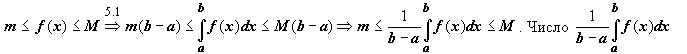
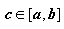 заключено между минимальным и максимальным значениями функции на отрезке. Одно из свойств функции, непрерывной на отрезке, заключается в том, что эта функция принимает любое значение, расположенное между m и M. Таким образом, существует точка, такая что
заключено между минимальным и максимальным значениями функции на отрезке. Одно из свойств функции, непрерывной на отрезке, заключается в том, что эта функция принимает любое значение, расположенное между m и M. Таким образом, существует точка, такая что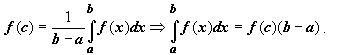
 Это свойство имеет простую геометрическую интерпретацию: если f(x) ≥ 0 непрерывна на отрезке [a,b], то существует точка такая, что площадь криволинейной трапеции ABCD равна площади прямоугольника с основанием [a,b] и высотой f(c) (на рисунке выделен цветом).
Это свойство имеет простую геометрическую интерпретацию: если f(x) ≥ 0 непрерывна на отрезке [a,b], то существует точка такая, что площадь криволинейной трапеции ABCD равна площади прямоугольника с основанием [a,b] и высотой f(c) (на рисунке выделен цветом). Находя границы для интеграла, мы, как говорят, производим его оценку. Может случиться, что весьма трудно или даже невозможно найти точное значение интеграла, а оценивая его, мы узнаем, хотя бы грубо, приближенное его значение. С такого рода оценками приходится довольно часто встречаться в математике.
Находя границы для интеграла, мы, как говорят, производим его оценку. Может случиться, что весьма трудно или даже невозможно найти точное значение интеграла, а оценивая его, мы узнаем, хотя бы грубо, приближенное его значение. С такого рода оценками приходится довольно часто встречаться в математике.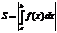 .
.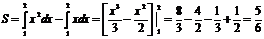 (ед2)
(ед2)