

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...
Топ:
Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда...
Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре...
Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает...
Интересное:
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
1. Находим определитель исходной матрицы. Если, то матрица - вырожденная и обратной матрицы  не существует. Если
не существует. Если 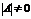 , то матрица
, то матрица 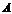 невырожденная и обратная матрица существует.
невырожденная и обратная матрица существует.
2. Находим матрицу, транспонированную к.
3. Находим алгебраические дополнения элементов и составляем из них присоединенную матрицу 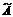 .
.
4. Составляем обратную матрицу по формуле 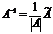 .
.
5. Проверяем правильность вычисления обратной матрицы 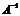 , исходя из ее определения:
, исходя из ее определения: 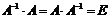 .
.
Пример. Найти матрицу, обратную данной: 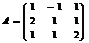 .
.
Р е ш е н и е.
1) Определитель матрицы
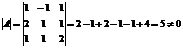 .
.
2) Находим алгебраические дополнения элементов матрицы и составляем из них присоединенную матрицу  :
:
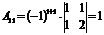
| 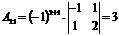
| 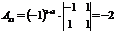
| 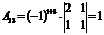
| 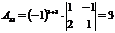
|
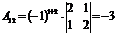
| 
| 
| 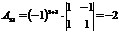
|
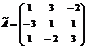 .
.
3) Вычисляем обратную матрицу:
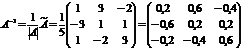 ,
,
4) Проверяем:
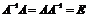 .
.
4. Система п линейных уравнений с п переменными (общий вид). Матричная форма записи такой системы. Решение системы (определение). Совместные и несовместные, определенные и неопределенные системы линейных уравнений.
Решение системы  линейных уравнений с
линейных уравнений с 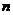 неизвестными
неизвестными
Системы линейных уравнений находят широкое применение в экономике.
Система 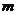 линейных уравнений с
линейных уравнений с 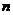 переменными имеет вид:
переменными имеет вид:
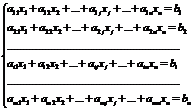 ,
,
где  (
( ) - произвольные числа, называемые коэффициентами при переменных и свободными членами уравнений, соответственно.
) - произвольные числа, называемые коэффициентами при переменных и свободными членами уравнений, соответственно.
Краткая запись: 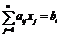 (
(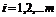 ).
).
Определение. Решением системы называется такая совокупность значений 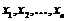 , при подстановке которых каждое уравнение системы обращается в верное равенство.
, при подстановке которых каждое уравнение системы обращается в верное равенство.
1) Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.
2) Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
|
|
3) Две системы уравнений называются равносильными (эквивалентными), если они имеют одно и то же множество решений (например, одно решение).
Запишем систему в матричной форме:
Обозначим:, где
А – матрица коэффициентов при переменных, или матрица системы, Х – матрица-столбец переменных, В – матрица-столбец свободных членов.
Т.к. число столбцов матрицы равно числу строк матрицы, то их произведение:
Есть матрица-столбец. Элементами полученной матрицы являются левые части начальной системы. На основании определения равенства матриц начальную систему можно записать в виде:.
Теорема Крамера. Пусть 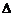 - определитель матрицы
- определитель матрицы 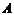 системы, а
системы, а 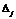 - определитель матрицы, получаемой из матрицы
- определитель матрицы, получаемой из матрицы 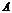 заменой
заменой 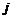 -го столбца столбцом свободных членов. Тогда, если
-го столбца столбцом свободных членов. Тогда, если 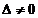 , то система имеет единственное решение, определяемое по формулам:
, то система имеет единственное решение, определяемое по формулам:
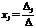 ,
,  - формула Крамера.
- формула Крамера.
Пример. Решить систему уравнений по формулам Крамера
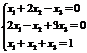
Р е ш е н и е. Определитель матрицы системы 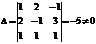 . Следовательно, система имеет единственное решение. Вычислим
. Следовательно, система имеет единственное решение. Вычислим  , полученные из
, полученные из  заменой соответственно первого, второго, третьего столбцов столбцом свободных членов:
заменой соответственно первого, второго, третьего столбцов столбцом свободных членов:
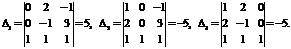
По формулам Крамера:
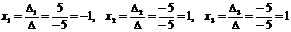 .
.
5. Метод Гаусса решения системы n линейных уравнений с п переменными. Понятие о методе Жордана – Гаусса.
Метод Гаусса - метод последовательного исключения переменных.
Метод Гаусса заключается в том, что с помощью элементарных преобразований строк и перестановок столбцов система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Преобразования Гаусса удобно проводить не с самими уравнениями, а с расширенной матрицей их коэффициентов 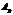 , получаемой приписыванием к матрице
, получаемой приписыванием к матрице 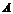 столбца свободных членов
столбца свободных членов 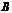 :
:
 .
.
Следует отметить, что методом Гаусса можно решить любую систему уравнений вида  .
.
Пример. Методом Гаусса решить систему:
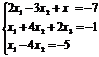
Выпишем расширенную матрицу системы.
|
|
Шаг 1. Поменяем местами первую и вторую строки, чтобы 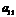 стал равным 1.
стал равным 1.
Шаг 2. Умножим элементы первой строки на (–2) и (–1) и прибавим их к элементам второй и третьей строк, чтобы под элементом 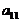 в первом столбце образовались нули.
в первом столбце образовались нули.
Шаг 3. Умножим элементы третьей строки на (–0,5).
Шаг 4. Поменяем местами вторую и третью строки.
Шаг 5. Поменяем местами второй и третий столбец. (Шаги 3, 4, 5 приведены с тем, чтобы 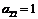 ).
).
Шаг 6. Элементы второй строки умножим на 3 и прибавим их к элементам третьей строки, тогда под элементом 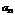 появится нуль.
появится нуль.
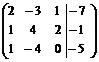 (называется расширенная матрица системы)
(называется расширенная матрица системы) 
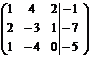

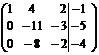

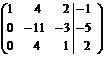

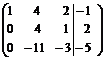

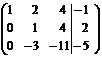

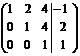 .
.
Расширенная матрица приведена к треугольному виду. Соответствующая ей система имеет вид:
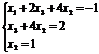
Из последнего уравнения 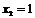 ; из второго
; из второго 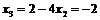 ; из первого
; из первого 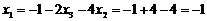 .
.
Таким образом, 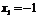 ,
, 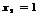 ,
, 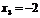 .
.
6. Решение систем п линейных уравнений с п переменными с помощью обратной матрицы (вывод формулы Х=А –1 В).
Для получения решения системы  при
при 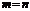 в общем виде предположим, что квадратная матрица системы
в общем виде предположим, что квадратная матрица системы 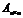 невырожденная, т.е. ее определитель
невырожденная, т.е. ее определитель 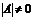 . В этом случае существует обратная матрица
. В этом случае существует обратная матрица 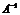 .
.
Метод обратной матрицы.
Запишем систему в матричной форме:
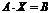 , где
, где
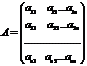 - матрица коэффициентов при переменных,
- матрица коэффициентов при переменных,
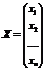 - матрица-столбец переменных;
- матрица-столбец переменных; 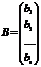 - матрица столбец свободных членов.
- матрица столбец свободных членов.
Умножим слева обе части равенства на матрицу 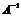 :
:
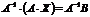 ;
;
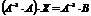 ;
;
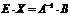 ;
;
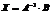 .
.
Таким образом, решение системы в матричном виде 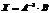 .
.
Пример. Решить систему уравнений методом обратной матрицы. 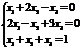
Р е ш е н и е: Обозначим 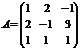 ;
; 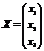 ;
; 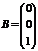 .
.
Тогда в матричной форме система имеет вид: 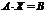 . Определитель матрицы
. Определитель матрицы 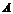
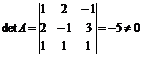 , т.е. обратная матрица
, т.е. обратная матрица 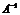 существует:
существует: 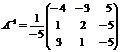 .
.
Определим 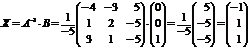 ,
,
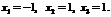
Существенным недостатком решения систем 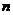 линейных уравнений с
линейных уравнений с 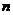 переменными по формулам Крамера и методом обратной матрицы является их большая трудоемкость, связанная с вычислением определителей и нахождения обратной матрицы.
переменными по формулам Крамера и методом обратной матрицы является их большая трудоемкость, связанная с вычислением определителей и нахождения обратной матрицы.
7. Теорема и формулы Крамера решения системы п линейных уравнений с п переменными (без вывода).
Теорема Крамера. Пусть - определитель матрицы системы, а - определитель матрицы, получаемой из матрицы заменой -го столбца столбцом свободных членов. Тогда, если, то система имеет единственное решение, определяемое по формулам:
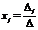 , (
, (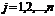 ).
).
В соответствии с обратной матрицей, где - матрица, присоединенная к матрице. Т.к. элементы матрицы есть алгебраические дополнения элементов матрицы, транспонированной к, то запишем равенство 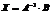 в развернутой форме:
в развернутой форме:
|
|
.
Учитывая, что, получим после умножения матриц:
, откуда следует, что для любого.
На основании свойства 9 определителей, где - определитель матрицы, полученной из матрицы заменой -го столбца столбцом свободных членов. Следовательно 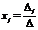 .
.
Решение системы  линейных уравнений с
линейных уравнений с 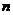 неизвестными
неизвестными
Рассмотрим систему 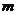 линейных уравнений с
линейных уравнений с 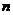 неизвестными.
неизвестными.
Теорема Кронекера-Капелли. Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы этой системы: 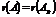 .
.
Для совместных систем линейных уравнений верны следующие теоремы:
Теорема 1. Если ранг матрицы совместной системы равен числу переменных, т.е. 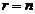 , то система имеет единственное решение.
, то система имеет единственное решение.
Теорема 2. Если ранг матрицы совместной системы меньше числа переменных, т.е. 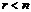 , то система является неопределенной и имеет бесконечное множество решений.
, то система является неопределенной и имеет бесконечное множество решений.
Определение. Базисным минором матрицы называется любой ненулевой минор, порядок которого равен рангу матрицы.
Определение. Те 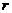 неизвестных, коэффициенты при которых входят в запись базисного минора, называются базисными (или основными), остальные
неизвестных, коэффициенты при которых входят в запись базисного минора, называются базисными (или основными), остальные 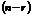 неизвестных называются свободными (или неосновными).
неизвестных называются свободными (или неосновными).
Решить систему уравнений в случае 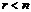 - это значит выразить базисные переменные через свободные. При этом имеем общее решение системы уравнений. Если все
- это значит выразить базисные переменные через свободные. При этом имеем общее решение системы уравнений. Если все 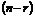 свободные переменные равны нулю, то решение системы называется базисным.
свободные переменные равны нулю, то решение системы называется базисным.
Пример. Решить систему методом Гаусса: 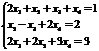
Р е ш е н и е. Выпишем и преобразуем расширенную матрицу системы. Сначала прибавим к элементам третьей строки элементы первой строки, умноженные на –1. А затем элементы второй строки умножим на –1 и прибавим к элементам третьей строки:
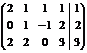

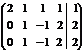

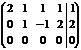 .
.
Расширенная матрица приведена к ступенчатому виду.
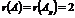 . Так как ранг матрицы равен 2, а количество неизвестных равно 4, то система имеет бесконечное множество решений. В качестве базисных неизвестных возьмем
. Так как ранг матрицы равен 2, а количество неизвестных равно 4, то система имеет бесконечное множество решений. В качестве базисных неизвестных возьмем 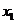 и
и 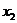 (т.к. определитель, составленный из их коэффициентов не равен нулю
(т.к. определитель, составленный из их коэффициентов не равен нулю 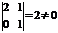 ), тогда
), тогда 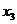 и
и 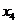 - свободные неизвестные.
- свободные неизвестные.
Выразим базисные переменные через свободные.
Из второй строки полученной матрицы выразим переменную 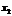 :
:
|
|
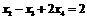 ,
, 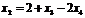 .
.
Из первой строки выразим 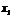 :
: 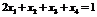 ,
,
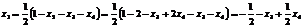 .
.
Общее решение системы уравнений: 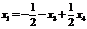 ,
, 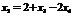 .
.
8. Понятие функции, способы задания функций. Область определения. Четные и нечетные, ограниченные, монотонные функции. Примеры.
|
|
|

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!