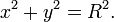Пусть функция f (x) непрерывна на замкнутом интервале [ a, b ]. Определенный интеграл от функции f (x) в пределах от a до b вводится как предел суммы бесконечно большого числа слагаемых, каждое из которых стремится к нулю.
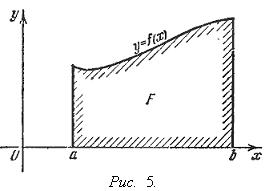
Геометрический смысл определенного интеграла. Если f (x) непрерывна и положительна на [ a, b ], то интеграл
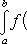
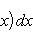
представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f (x) (см. рис. 5.).
10. Определённый интеграл. Основные свойства определённого интеграла.
Пусть функция f (x) непрерывна на замкнутом интервале [ a, b ]. Определенный интеграл от функции f (x) в пределах от a до b вводится как предел суммы бесконечно большого числа слагаемых, каждое из которых стремится к нулю.
Свойства определенного интеграла:
Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. 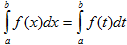 , где х, t – любые буквы.
, где х, t – любые буквы.
Определенный интеграл с одинаковыми пределами интегрирования равен нулю.
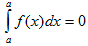
При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.
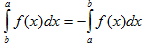
Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.
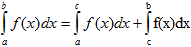
Постоянный множитель можно выносить за знак определенного интеграла.
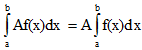
Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.
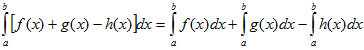
11. Понятие комбинаторных задач. Размещения, перестановки, сочетания.
Комбинаторика - это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиальновозможное количество различных вариантов развития событий.
Размещениями из  элементов по
элементов по  называются соединения, которые можно образовать из
называются соединения, которые можно образовать из 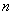 элементов, собирая в каждое соединение по
элементов, собирая в каждое соединение по 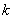 элементов, при этом соединения могут отличаться друг от друга как самими элементами, так и порядком их расположения.
элементов, при этом соединения могут отличаться друг от друга как самими элементами, так и порядком их расположения.
Число всех возможных размещений, которые можно образовать из 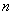 элементов по
элементов по 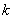 , обозначается символом
, обозначается символом 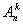 и вычисляется по формуле:
и вычисляется по формуле:
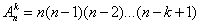 ,
,
(всего k множителей).
Перестановками из n элементов называются соединения, каждое из которых содержит все n элементов, отличающихся поэтому друг от друга только порядком расположения элементов.
Число всех возможных перестановок, которые можно образовать из n элементов, обозначается символом 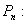
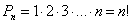
Сочетаниями из n элементов по k называются соединения, которые можно образовать из n элементов, собирая в каждое соединение k элементов; при этом соединения отличаются друг от друга только самими элементами (различие порядка их расположения во внимание не принимается).
Число всех возможных сочетаний, которые можно образовать из n элементов по k, обозначается символом 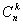 :
:
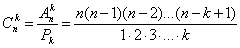
12. Случайное событие. Виды случайных событий. Классическое определение вероятности.
Случайное событие — подмножество исходов случайного эксперимента; при многократном повторении эксперимента частота наступления события служит оценкой его вероятности.
Случайное событие, которое никогда не реализуется в результате эксперимента, называется невозможным.
Случайное событие, которое всегда реализуется в результате эксперимента, называется достоверным.
Случайные события называются несовместными в данном испытании, если никакие два из них не могут появиться вместе.
Случайные события образуют полную группу, если при каждом испытании может появиться любое из них и не может появиться какое-либо иное событие, несовместное с ними.
Под классическим определением вероятностей подразумевают выбор такого конечного вероятностного пространства, в котором все элементарные исходы равновероятны:
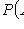
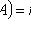
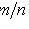
13. Понятие вектора. Сумма и разность векторов. Умножение вектора на число.
Вектором (в реальном пространстве) называется направленный отрезок 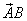 с начальной точкой
с начальной точкой 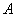 и конечной точкой
и конечной точкой 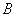 , который можно передвигать параллельно самому себе.
, который можно передвигать параллельно самому себе.
Длиной 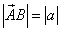 вектора
вектора 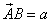 называется число (неотрицательное), равное длине отрезка
называется число (неотрицательное), равное длине отрезка 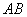 , соединяющего точки
, соединяющего точки 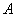 и
и 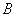 . Вектор нулевой длины называется нулевым.
. Вектор нулевой длины называется нулевым.
Вектор BA, равный по длине вектору AB и противоположно направленный, называется противоположным.
Вектор, длина которого равна 1, называется единичным. Единичный вектор, направление которого совпадает с направлением вектора AB, называется ортом вектора AB
Векторы, лежащие на праллельных или совпадающих прямых, называются коллинеарными.
Векторы, лежащие в праллельных или совпадающих плоскостях, называются компланарными. Если угол между векторами равен π /2, то векторы называются ортогональными.
Суммой двух векторов 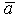 и
и 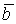 называется вектор
называется вектор 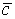 , направленный из начала вектора
, направленный из начала вектора 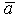 в конец вектора
в конец вектора 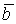 при условии, что начало
при условии, что начало 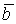 совпадет с концом вектора
совпадет с концом вектора 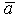 . Если векторы заданы их разложениями по базисным ортам, то при сложении векторов складываются их соответствующие координаты.
. Если векторы заданы их разложениями по базисным ортам, то при сложении векторов складываются их соответствующие координаты.
Разностью двух векторов 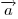 и
и 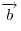 называется такой вектор
называется такой вектор 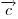 , который будучи сложенным с вектором
, который будучи сложенным с вектором 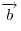 , даст
, даст 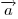 . Разность двух векторов
. Разность двух векторов 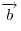 и
и 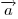 представляется направленным отрезком, соединяющим концы этих векторов и имеющим направление «к концу того вектора, из которого вычитают».
представляется направленным отрезком, соединяющим концы этих векторов и имеющим направление «к концу того вектора, из которого вычитают».
Произведение ненулевого вектора на число - это вектор, коллинеарный данному, а его модуль равен модулю данного вектора, умноженному на модуль числа.
Произведение ненулевого вектора на число - это вектор, координаты которого равны соответствующим координатам данного вектора, умноженным на число.
14. Декартова система координат. Разложение вектора по базису. Координаты и длина вектора.
Прямоугольная система координат, в которой единицы измерения по всем осям равны друг другу, называется ортонормированной (декартовой) системой координат.
Координатой точки A по оси x будем называть число, равное по абсолютной величине длине отрезка OAx: положительное, если точка A лежит на положительной полуоси x, и отрицательное, если она лежит на отрицательной полуоси.
Аналогично можно определить координаты y и z точки A. Координаты точки A записываются в скобках рядом с названием этой точки: A (x; y; z).
Единичным вектором или ортом называется вектор, длина которого равна единице и который направлен вдоль какой-либо координатной оси.
- Единичный вектор, направленный вдоль оси x, обозначается i
 .
. - Единичный вектор, направленный вдоль оси y, обозначается j
 .
. - Единичный вектор, направленный вдоль оси z, обозначается k
 .
.
Вектора i  , j
, j  , k
, k  называются координатными векторами.
называются координатными векторами.
- Любой вектор a
 можно разложить по координатным векторам: a
можно разложить по координатным векторам: a  = x
= x  i
i  + y
+ y  j
j  + z
+ z  k.
k. - Коэффициенты разложения определяются единственным образом и называются координатами вектора a
 в данной системе координат.
в данной системе координат.
Длиной или модулем вектора называется длина отрезка, изображающего данный вектор. Длиной нулевого вектора называется число нуль.
Длина вектора на плоскости вычисляется по следующей формуле:
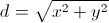
Длина вектора в трехмерном пространстве вычисляется по следующей формуле:
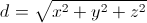
15. Скалярное произведение векторов и его свойства. Условие перпендикулярности векторов.
Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла междуними.
Обозначается ab,а* b(или(а, b)). Итак, по определению,
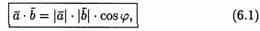
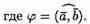
Формуле (6.1) можно придать иной вид. Так как | a| cosg=пр ba, (см. рис.14), a |b| cosg = пр ab, то получаем:

т. е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.
Скалярное произведение имеет свойства, аналогичные свойствам произведений чисел:
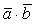
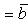
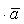
(переместительное свойство умножения);
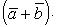
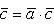
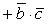
(распределительное, или дистрибутивное свойство произведения).
Если векторы 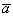 и
и 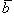 заданы проекциями на координатные оси
заданы проекциями на координатные оси
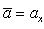
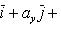
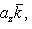
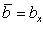
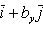
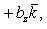
то их скалярное произведение вычисляется по формуле
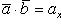
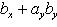
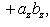
а косинус угла 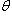 между этими векторами определяется по формуле
между этими векторами определяется по формуле

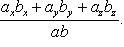
Если углы, образуемые вектором 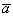 с координатными осями, обозначить через
с координатными осями, обозначить через 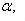
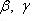 , а углы, образуемые вектором
, а углы, образуемые вектором 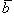 с координатными осями, - через
с координатными осями, - через 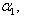
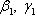 , то косинус угла
, то косинус угла 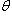 между векторами
между векторами 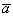 и
и 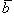 определяется по формуле
определяется по формуле
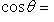
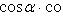
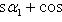
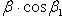
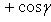
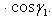
Если векторы 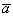 и
и 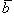 перпендикулярны, то их скалярное произведение равно нулю, и тогда
перпендикулярны, то их скалярное произведение равно нулю, и тогда
axbx + ayby + azbz = 0,
или
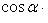
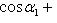
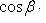
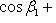
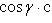
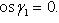
Два ненулевых вектора называются перпендикулярными, если угол между ними равен девяноста градусам (П/2 радиан).
Необходимое и достаточное условие перпендикулярности двух векторов:
Для перпендикулярности двух ненулевых векторов 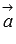 и
и  необходимо и достаточно, чтобы их скалярное произведение равнялось нулю, то есть, чтобы выполнялось равенство
необходимо и достаточно, чтобы их скалярное произведение равнялось нулю, то есть, чтобы выполнялось равенство 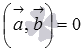 .
.
16. Угол между векторами.
Угол между векторами — угол между направлениями этих векторов (наименьший угол).
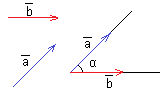
По определению, угол между двумя векторами находится в промежутке [0°; 180°].
Угол между векторами 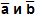 обозначается так:
обозначается так: 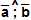 .
.
Если векторы перпендикулярны, то угол между ними равен 90º. Если векторы сонаправлены, в частности один из них или оба нулевые, то угол между ними равен 0о. Если противоположно направленные векторы, то угол между ними равен 180º.
Угол между двумя ненулевыми векторами находится с помощью вычисления скалярного произведения. По определению скалярное произведение равно произведению длин векторов на косинус угла между ними (скалярное произведение для двух векторов с координатами (x1; y1) и (x2; y2) вычисляется по формуле: x1x2 + y1y2).
17. Уравнение окружности в общем виде (частные случаи). Уравнение сферы.
Общее уравнение окружности записывается как:
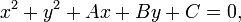
или
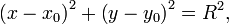
где
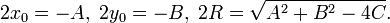
Точка 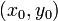 — центр окружности,
— центр окружности, 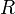 — её радиус.
— её радиус.
Уравнение окружности радиуса 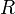 с центром в начале координат:
с центром в начале координат:
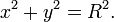
Сфера радиуса R с центром в начале координат представлена уравнением второй степени.
x 2 + y 2 + z 2 = R 2.
Сфера радиуса R центр которой не совпадает с началом координат представлена другим уравнением второй степени.
(x – a)2 + (y – b)2 + (z – c)2 = R 2.
18. Общее уравнение прямой. Частные случаи общего уравнения прямой.
Любая прямая на плоскости может быть задана уравнением первого порядка
Ах + Ву + С = 0,
причем постоянные А, В не равны нулю одновременно. Это уравнение первого порядка называют общим уравнением прямой. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:
• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат
• А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох
• В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу
• В = С = 0, А ≠0 – прямая совпадает с осью Оу
• А = С = 0, В ≠0 – прямая совпадает с осью Ох
Уравнение прямой может быть представлено в различном виде в зависимости от каких – либо заданных начальных условий.
19. Аксиомы стереометрии и следствия из них.
Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве.
Аксиома 1.
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Аксиома 2.
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит через прямую).
Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.
Аксиома 3.
Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
В таком случае говорят, плоскости пересекаются по прямой.
Пример: пересечение двух смежных стен, стены и потолка комнаты.
Следствия:
Теорема 1.
Через прямую a и не лежащую на ней точку А проходит плоскость, и притом только одна.
Теорема 2.
Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна.
20. Параллельность прямых и плоскостей. Признак параллельности двух плоскостей.
Прямая и плоскость называются параллельными, если они не имеют общих точек.
Если прямая a параллельна плоскости α, то пишут a || α.



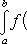
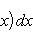

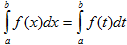 , где х, t – любые буквы.
, где х, t – любые буквы.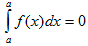
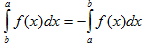
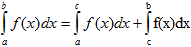
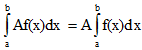
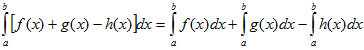
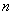 элементов по
элементов по 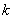 называются соединения, которые можно образовать из
называются соединения, которые можно образовать из 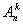 и вычисляется по формуле:
и вычисляется по формуле: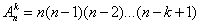 ,
,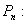
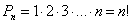
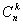 :
: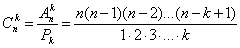
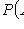
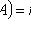
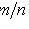
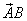 с начальной точкой
с начальной точкой 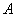 и конечной точкой
и конечной точкой 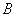 , который можно передвигать параллельно самому себе.
, который можно передвигать параллельно самому себе.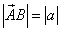 вектора
вектора 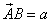 называется число (неотрицательное), равное длине отрезка
называется число (неотрицательное), равное длине отрезка 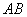 , соединяющего точки
, соединяющего точки 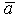 и
и 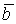 называется вектор
называется вектор 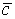 , направленный из начала вектора
, направленный из начала вектора 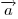 и
и 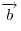 называется такой вектор
называется такой вектор 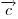 , который будучи сложенным с вектором
, который будучи сложенным с вектором  .
. i
i 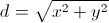
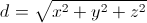
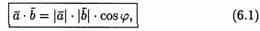
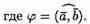


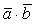
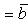
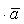
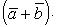
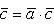
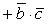
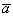 и
и 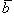 заданы проекциями на координатные оси
заданы проекциями на координатные оси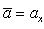
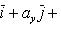
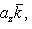
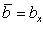
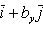
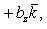
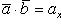
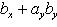
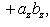
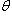 между этими векторами определяется по формуле
между этими векторами определяется по формуле
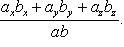
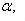
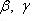 , а углы, образуемые вектором
, а углы, образуемые вектором 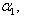
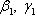 , то косинус угла
, то косинус угла 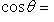
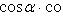
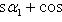
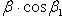
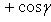
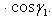
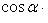
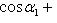
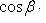
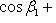
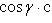
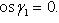
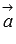 и
и  необходимо и достаточно, чтобы их скалярное произведение равнялось нулю, то есть, чтобы выполнялось равенство
необходимо и достаточно, чтобы их скалярное произведение равнялось нулю, то есть, чтобы выполнялось равенство 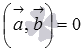 .
.
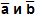 обозначается так:
обозначается так: 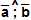 .
.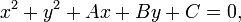
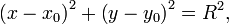
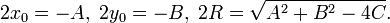
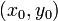 — центр окружности,
— центр окружности, 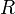 — её радиус.
— её радиус.