Статистические свойства случайных процессов

Случайный процесс (СП) Х (t) задается, в общем случае, ансамблем своих реализаций, то есть бесконечным множеством потенциально возможных случайных функций времени х(t), в рамках указанного процесса, с указанием вероятностей их появления (см.рис.1 (3.8 на стр.29). На практике такой подход неосуществим и СП задается некоторыми усредненными (статистическими) характеристиками, отражающими те или иные свойства этого процесса.

Наиболее частот для описания СП используются одномерные законы распределения значений СП, определяемые для ансамбля реализаций в один фиксированный момент времени (в одном сечении). Объектом для усреднения является бесконечное множество значений (чисел) случайного процесса - выборка значений СП.

Законы распределения значений могут меняться от сечения к сечению, а могут и оставаться неизменными. В первом случае СП считается нестационарным, а во втором - стационарным. Сечение от сечения надо выбирать через такой интервал времени Dt, чтобы выборки значений СП в смежных сечениях были статистическими не связаны между собой (некоррелированы). Следовательно, стационарный случайный процесс может быть задан своими характеристиками, определенными лишь для одного сечения. Наиболее широко используются два одномерных закона распределения мгновенных значений СП:

-интегральный закон распределения F(x) - (функция распределения);

-дифференциальный закон w(х) закон распределения плотности вероятности;

Интегральный закон показывает для каждого конкретного значения х, взятого из {x}, вероятность события, заключающегося в том, что наблюдаемая случайная величина х меньше или равна наперед заданного значения х:

F (x) = P[x £ x] (1)

Закон распределения плотности вероятности показывает для каждого конкретного значения х вероятность события, заключающегося в том, что наблюдаемое значение Х попадает в бесконечно малый интервал значений Dх вокруг значения х: Dх ® 0 (2)

Дифференциальный и интегральный законы однозначно связаны между собой: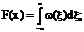

(рис.2 Пример взаимосвязанных законов распределения).

На интегральный закон распределения вероятностей положены следующие ограничения: 1) 0 £ F(x) £ 1 при -¥ < х < + ¥

2) F(-¥) = 0; F(+ ¥) = 1

3) F(x) не уменьшается при возрастании х

4) P[x, < C £ x₂ ] = F(x₂) - F(x₁)

Очень часто используют не саму функцию F(x), а ее производную, т.е. распределение плотности вероятности w(х).

Вероятность появления конкретного значения х исчезающе мала, однако попадание значений СП в интервал Dх есть вполне конкретная величина, зависящая как от самого значения х и интервала Dх, так и от вида функции w(х).

Основные свойства закона распределения плотности вероятности мгновенных значений СП:

1) P(x) ³ 0 при - ¥ < х < + ¥; - условие нормировки < х £ х₂]

4) математическое ожидание m_x = значений случайного процесса находится путем статистического усреднения по ансамблю: (3)

5) мерой разброса значений СП относительно своего среднего служит второй центральный момент или дисперсия: (4)

Величина называется среднеквадратическим отклонением и служит для количественного описания меры разброса отдельных значений относительно выборочного среднего.

Для стационарных процессов m_x имеет смысл постоянной составляющей этого процесса, а - средней мощности переменной составляющей.

Стационарные СП, для которых усреднение по ансамблю может быть заменено усреднением по времени, называются эргодическими. Для таких процессов операция усреднения выполняется над единственной реализацией x(t), протяженность которой стремиться к бесконечности

В качестве примера на рис.3 (3.10, с.32) приведены и для меандра (квадратной волны) и треугольной волны.

Среди различных законов распределения вероятностей особое место занимает нормальное (или гауссово) распределение, которое является очень удобной математической моделью реальных СП, особенно типа флуктуационных (шумоподобных). Согласно центральной предельной теореме теории вероятностей (теорема Ляпунова) закон распределения СП, представляющего из себя сумму бесконечно большого числа одинаковых по малости СП, стремится к нормальному, независимо от законов распределения слагаемых.

Закон распределения плотности вероятности нормального СП имеет вид:

(5)

Множитель перед экспонентой появляется из-за необходимости выполнения условия нормировки, так как

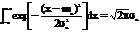
Вид кривых w(х) и F(x) для нормального процесса зависит от величины стандартного отклонения s_х и среднего значения m_x (рис.4, рис.3.11 стр. 34).

Все кривые нормально распределенных процессов с разными мощностями могут быть сведены к стандартному виду, если в качестве переменной взять , тогда значение СП будут выражаться не в абсолютных величинах (вольтах, амперах. а в долях от стандартного отклонения s_х (рис.5, рис. 3.12 с. 34) С

Следовательно: гдеÆ - хорошо изученная и затабулированная функция называемая интегралом вероятностей или функцией ошибок erf(u).

Выражение для закона распределения плотности вероятности в новых переменных:

Вероятность попадания нормально распределенной случайной величины в интервал: -s_х ¸ s_х» 0,683

-2s_х ¸ 2s_х» 0,954

-3s_х ¸ 3s_х» 0,997

Предельным случаем w(х) нормально распределенного процесса при s_х®0 является так называемый дельта-импульс d (х-m_x), представляющий из себя бесконечно узкий, но и бесконечно высокий импульс с площадью, равной единице и расположенный в точке х=m_x.

Часто пользуются обратной функцией ошибок Q(u) = 1 - Æ(u) = erfc (u), которая характеризует вероятность, с которой значения СП превысят наперед заданное значение U.

Иногда используется другая функция ошибок, функция Крампа:

30) Энергетические спектры сигналов

Рассмотрим частотный аспект и найдем связь между скалярным произведением сигналов и их спектральными плотностями. Пусть имеются два сигнала u(t) и V(t). Их скалярное произведение (u,v)= пропорционально взаимной энергии сигналов и, если сигналы совпадают, т.е. u(t) = v(t), то скалярное произведение переходит в энергию сигнала:

. Каждому из сигналов u(t) и v(t) соответствуют спектральные плотности которые связаны с сигналами обратным преобразованием Фурье

 

Заменим в скалярном произведении один из сигналов его спектральным представлением а затем сменим порядок интегрирования по времени и частоте: Внутренний интеграл есть не что иное, как спектральная плотность сигнала u(t) при отрицательном значении аргумента (т.е. частоты): Следовательно . (1) Эта запись называется обобщенной формулой Рэлея.

Скалярное произведение двух сигналов пропорционально скалярному произведению их спектральных плотностей.(!)

Если u(t) = v(t), то из (1) получим так называемое равенство Парсеваля:

(2)

Равенство Парсеваля устанавливает связь между энергией сигнала и модулем его спектральной плотности. Величина имеет смысл плотности распределения энергии по оси частот и называется энергетическим спектром сигнала или спектральной плотностью энергии сигнала.

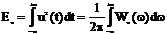(3)

т.е. энергия сигнала может быть представлена как результат суммирования вкладов в энергию от различных участков на частотной оси.

Аналогично определяется и взаимный энергетический спектр сигналов u(t) и v(t): (u,v)= (4)

Вид кривой взаимного энергетического сигнала спектра W_u,v(ω) показывает, какую роль в формировании взаимной энергии сигналов (их взаимного влияния) играют различные участки их спектра. При изучении сигналов с помощью энергетических спектров неизбежно теряется информация, которая заключена в фазовых спектрах, тем не менее понятие энергетического спектра весьма плодотворно с точки зрения установления реальной ширины спектра тех или иных сигналов.

Рассмотрим распределение энергии в спектре одиночного прямоугольного видеоимпульса. Аналитическое выражение для энергетического спектра можно получить, возводя в квадрат выражение для спектральной плотности прямоугольного видеоимпульса

(5)

 

Полная энергия такого видеоимпульса равна 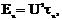где U- амплитуда импульса, τ_u - длительность.

Рисунок

Для определения доли энергии в пределах 1-го, 2-го, 3-го лепестков спектра надо проинтегрировать (5) в соответствующих пределах. Доля энергии в 1-ом лепестке

Сделаем замену переменных тогда . Имеется табличный интеграл однако в пределах от 0 до π этот интеграл не затабулирован. Численные расчеты показывают, что в пределах 1-го лепестка содержится 0,902 энергии сигнала, во 2-ом - 0,048, в 3-ьем - 0,023. Таким образом, 2-х краткое расширение полосы пропускания приемника увеличит энергию сигнала всего на 4,8%, в то время. как помеха, если она имеет равномерный спектр, увеличит свою энергию на 100 %. На практике принято за активную ширину спектра сигнала ΔF принимать диапазон частот, внутри которого сосредоточено 90 - 95% энергии сигнала. Для прямоугольного видеоимпульса это один-два первых лепестка.