Обратная матрица. Ранг матрицы.
Если для матрицы А существует матрица В, такая, что 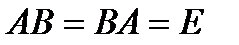 , где Е - единичная матрица, то матрица В называется обратной к матрице А.
, где Е - единичная матрица, то матрица В называется обратной к матрице А.
Из определения следует, что А и В – квадратные матрицы одинакового порядка. Матрицу, обратную к матрице А, будем обозначать А-1.
Невырожденной или неособенной матрицей называется квадратная матрица, определитель которой отличен от нуля. Если определитель матрицы равен нулю, то матрица называется вырожденной или особенной.
Для того, чтобы существовала матрица В, обратная матрице А, необходимо и достаточно, чтобы матрица А была невырожденной.
Определитель второго порядка, который получается из определителя  третьего порядка вычеркиванием
третьего порядка вычеркиванием 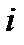 -й строки и
-й строки и  -го столбца, называется минором элемента
-го столбца, называется минором элемента 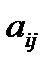 определителя
определителя  и обозначается
и обозначается  .
.
Алгебраическим дополнением элемента 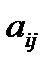 определителя
определителя  называется минор
называется минор  , взятый со знаком
, взятый со знаком 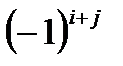 , обозначается
, обозначается 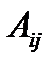 .
.
Итак, 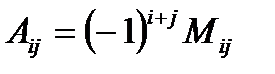 .
.
Обратная к данной матрица может быть получена следующим образом
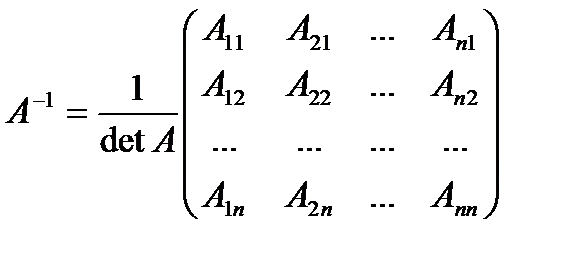 , где
, где

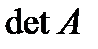 - определитель матрицы А,
- определитель матрицы А, 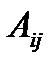 - алгебраические дополнения элементов матрицы А.
- алгебраические дополнения элементов матрицы А.
4.-5 Матричный метод и метод Крамера решения систем линейных уравнений.\
Линейным алгебраическим уравнением называют уравнение, содержащее переменную только в первой степени и не имеющее произведений переменных. При решении систем линейных уравнений используются определители и матрицы.
Пусть дана система трех линейных уравнений с тремя неизвестными:
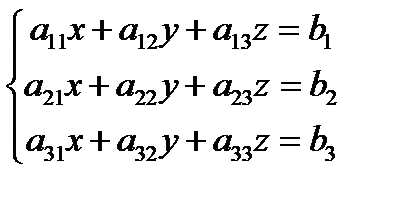
2.1. Метод Крамера
Введем определитель системы - 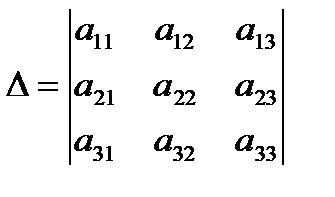 и дополнительные определители:
и дополнительные определители:
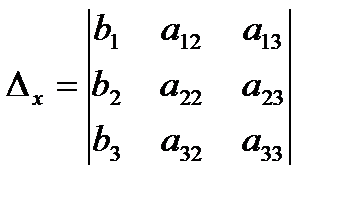 ,
, 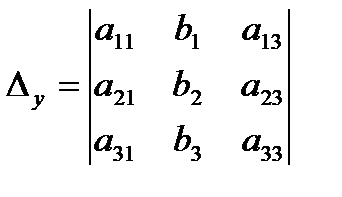 ,
, 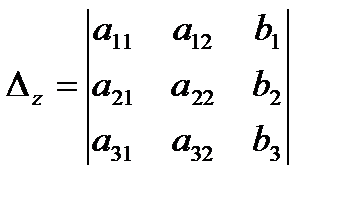 .
.
Если определитель системы 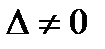 , то система имеет единственное решение, определяемое формулами Крамера:
, то система имеет единственное решение, определяемое формулами Крамера:
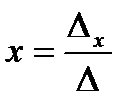 ,
,  ,
,  .
.
Метод Гаусса
Ранее рассмотренный метод Крамера можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.
Теорема Кронекера-Капелли: Для того, чтобы неоднородная система линейных алгебраических уравнений была совместна, необходимо и достаточно, чтобы ранг расширенной матрицы системы совпадал с рангом матрицы системы.
Однородная система уравнений всегда совместна, так как имеет нулевое решение  . Ненулевые решения она имеет тогда и только тогда, когда
. Ненулевые решения она имеет тогда и только тогда, когда 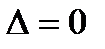 .
.
Прямая на плоскости
Всякая прямая относительно прямоугольной системы координат на плоскости определяется уравнением первой степени, и обратно, всякое уравнение первой степени относительно координат 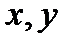 описывает некоторою прямую на плоскости.
описывает некоторою прямую на плоскости.
Любой ненулевой вектор, параллельный данной прямой, называется её направляющим вектором.
Различные способы задания прямой
Уравнение прямой, заданной точкой и направляющим вектором
Пусть дана некоторая прямая, которая проходит через точку 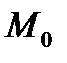 с известными координатами
с известными координатами 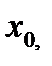 ,
, 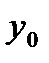 параллельно направляющему вектору
параллельно направляющему вектору 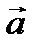 , координаты которого также известны и равны (
, координаты которого также известны и равны (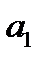 ,
, 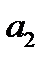 ).
).
Уравнение этой прямой можно записать в виде:
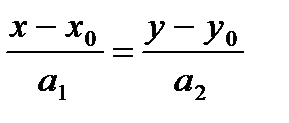 .
.
Это равенство называется каноническим уравнением прямой.
Параметрические уравнения прямой
Существует ещё один вид уравнения прямой, проходящей через данную точку 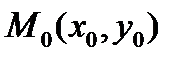 и имеющей данный направляющий вектор
и имеющей данный направляющий вектор 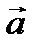
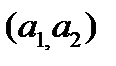 :
: 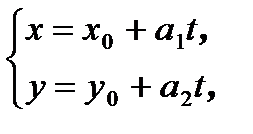
где 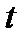 - параметр, принимающий все действительные значения.
- параметр, принимающий все действительные значения.
Этот вид называется параметрическими уравнениями прямой.
Уравнение прямой, проходящей через две заданные точки
Пусть некоторая прямая проходит через две точки с известными координатами: 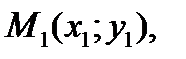
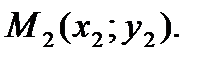 . Уравнение этой прямой имеет вид:
. Уравнение этой прямой имеет вид: 
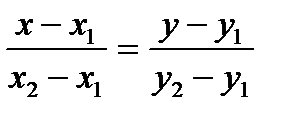 .
.
Уравнение прямой “в отрезках по осям”
Пусть прямая отсекает на оси 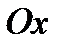 отрезок величины
отрезок величины 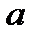 , на оси
, на оси 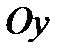 – отрезок
– отрезок 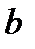 . В этом случае уравнение прямой будет иметь вид:
. В этом случае уравнение прямой будет иметь вид:
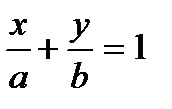 .
.
Расстояние от точки до прямой
Расстояние от точки 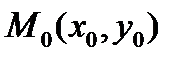 до прямой
до прямой 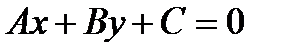 вычисляется по формуле
вычисляется по формуле
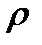 (
(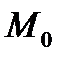 ,
, 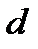 )=
)= 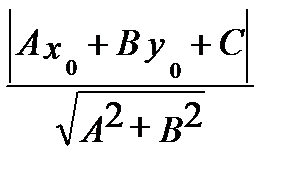 .
.
Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых
Тангенс угла между прямыми, уравнения которых относительно прямоугольной системы координат заданы в виде 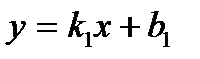 и
и 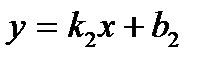 , вычисляется по формуле
, вычисляется по формуле
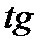
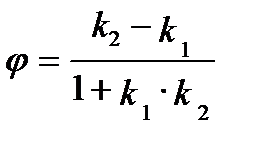 ,
,
причём угол принято отсчитывать против часовой стрелки от первой прямой ко второй.
Необходимое и достаточное условие параллельности заданных прямых выражается равенством 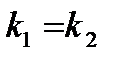 , а условие перпендикулярности
, а условие перпендикулярности 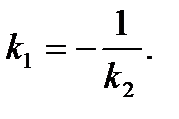
14 Способы задания плоскости в пространстве. Расстояние от точки до плоскости.
Всякая плоскость относительно некоторой прямоугольной системы координат в пространстве определяется уравнением первой степени и обратно: каждое уравнение первой степени определяет плоскость.
Различные способы задания плоскости
Уравнение плоскости, проходящей через заданную точку параллельно двум неколлинеарным векторам
Пусть относительно некоторой прямоугольной системы координат в пространстве дана точка M 0(x 0; y 0; z 0) некоторой плоскости и два неколлинеарных вектора 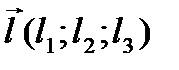 ,
, 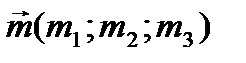 , параллельные этой плоскости.
, параллельные этой плоскости.
Тогда уравнение плоскости можно записать так:
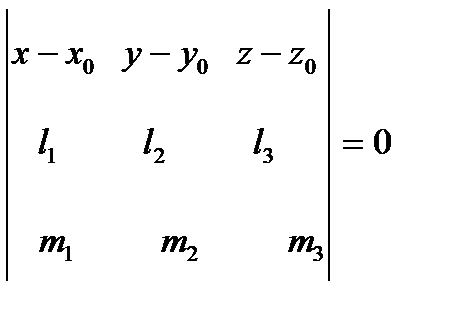
Прямая в пространстве
Вектор, параллельный прямой, называется направляющим вектором прямой.
Различные способы задания прямой
Уравнение прямой, проходящей через данную точку параллельно данному вектору.
Прямая, проходящая через точку M 0(x 0; y 0; z 0) параллельно направляющему вектору  , определяется или параметрическими уравнениями:
, определяется или параметрическими уравнениями:
x = x 0+ 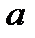 1 t,
1 t,
y = y 0+ 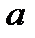 2 t,
2 t,
z = z 0+ 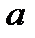 3 t,
3 t,
где t – параметр, принимающий произвольные значения, или каноническими уравнениями вида:
 .
.
(В этом уравнении отношения рассматриваются как пропорция, а не как дроби).
Комплексные числа
Комплексным числом z называется выражение вида: 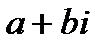 , где
, где 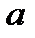 и
и 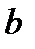 - действительные числа, а
- действительные числа, а 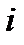 - комплексная единица, которая удовлетворяет условию
- комплексная единица, которая удовлетворяет условию 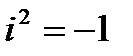 .
.
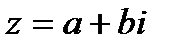 - алгебраическая форма записи комплексного числа,
- алгебраическая форма записи комплексного числа, 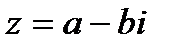 - комплексно-сопряженное число.
- комплексно-сопряженное число.
Пусть 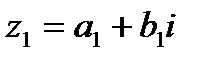 и
и 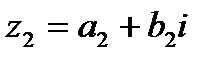 , тогда:
, тогда:
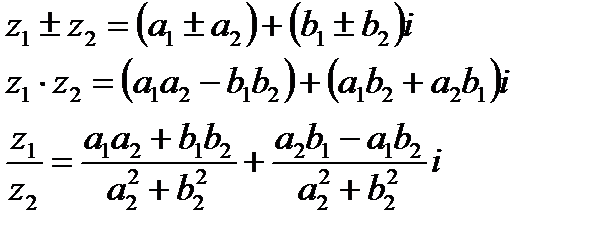
Тригонометрическая форма записи комплексного числа:
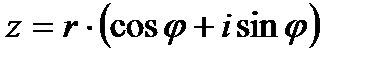 ,
,
где 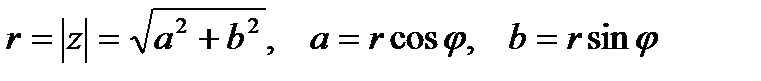 , при
, при 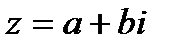 .
.
Аргумент 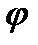 можно найти, используя формулу
можно найти, используя формулу 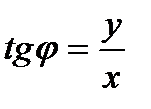 :
:
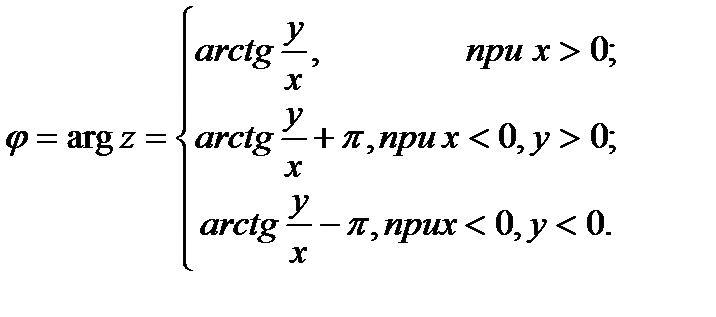
Пусть 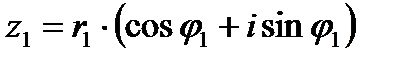 ,
, 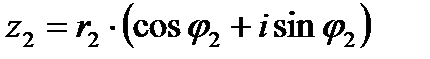 , тогда:
, тогда:
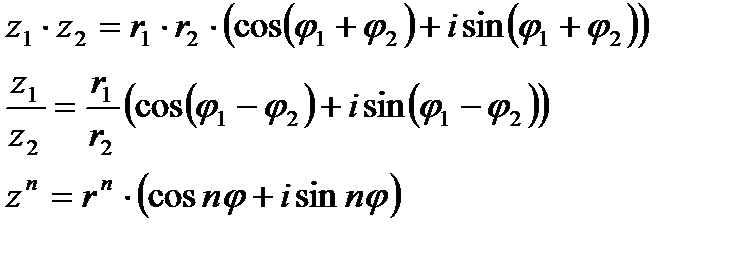
при 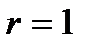 получаем формулу Муавра:
получаем формулу Муавра:
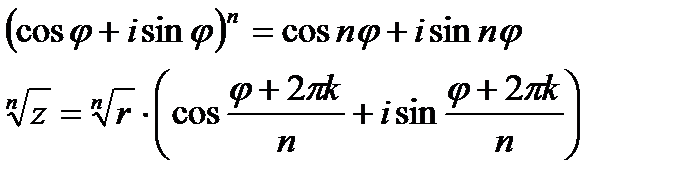 , где
, где 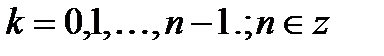 .
.
Пример:
Найти 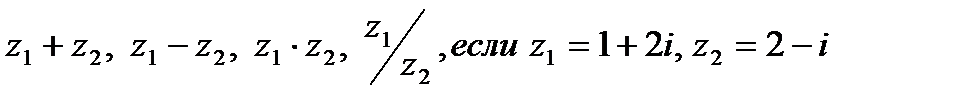
Решение:

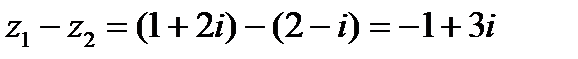
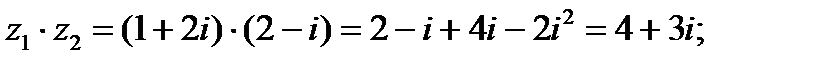
 .
.
Обратная матрица. Ранг матрицы.
Если для матрицы А существует матрица В, такая, что 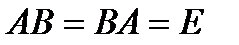 , где Е - единичная матрица, то матрица В называется обратной к матрице А.
, где Е - единичная матрица, то матрица В называется обратной к матрице А.
Из определения следует, что А и В – квадратные матрицы одинакового порядка. Матрицу, обратную к матрице А, будем обозначать А-1.
Невырожденной или неособенной матрицей называется квадратная матрица, определитель которой отличен от нуля. Если определитель матрицы равен нулю, то матрица называется вырожденной или особенной.
Для того, чтобы существовала матрица В, обратная матрице А, необходимо и достаточно, чтобы матрица А была невырожденной.
Определитель второго порядка, который получается из определителя  третьего порядка вычеркиванием
третьего порядка вычеркиванием  -й строки и
-й строки и  -го столбца, называется минором элемента
-го столбца, называется минором элемента 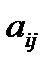 определителя
определителя  и обозначается
и обозначается  .
.
Алгебраическим дополнением элемента 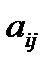 определителя
определителя  называется минор
называется минор  , взятый со знаком
, взятый со знаком 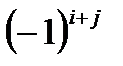 , обозначается
, обозначается 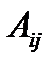 .
.
Итак, 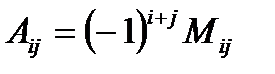 .
.
Обратная к данной матрица может быть получена следующим образом
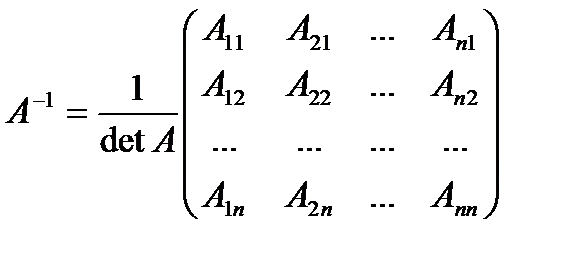 , где
, где

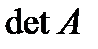 - определитель матрицы А,
- определитель матрицы А, 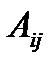 - алгебраические дополнения элементов матрицы А.
- алгебраические дополнения элементов матрицы А.
4.-5 Матричный метод и метод Крамера решения систем линейных уравнений.\
Линейным алгебраическим уравнением называют уравнение, содержащее переменную только в первой степени и не имеющее произведений переменных. При решении систем линейных уравнений используются определители и матрицы.
Пусть дана система трех линейных уравнений с тремя неизвестными:
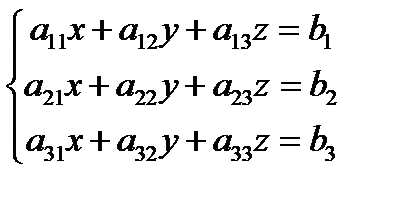
2.1. Метод Крамера
Введем определитель системы - 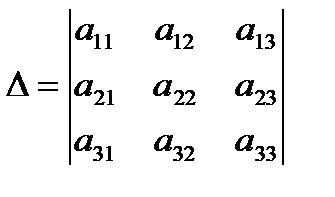 и дополнительные определители:
и дополнительные определители:
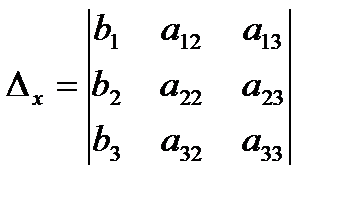 ,
, 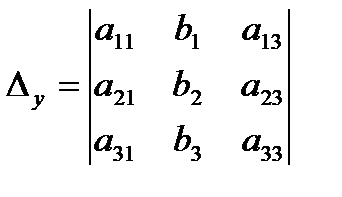 ,
, 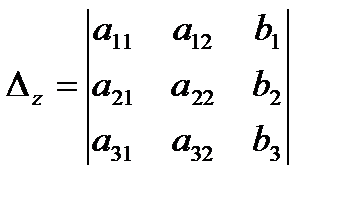 .
.
Если определитель системы 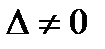 , то система имеет единственное решение, определяемое формулами Крамера:
, то система имеет единственное решение, определяемое формулами Крамера:
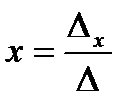 ,
,  ,
,  .
.
Метод Гаусса
Ранее рассмотренный метод Крамера можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.
Теорема Кронекера-Капелли: Для того, чтобы неоднородная система линейных алгебраических уравнений была совместна, необходимо и достаточно, чтобы ранг расширенной матрицы системы совпадал с рангом матрицы системы.
Однородная система уравнений всегда совместна, так как имеет нулевое решение  . Ненулевые решения она имеет тогда и только тогда, когда
. Ненулевые решения она имеет тогда и только тогда, когда 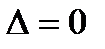 .
.



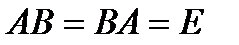 , где Е - единичная матрица, то матрица В называется обратной к матрице А.
, где Е - единичная матрица, то матрица В называется обратной к матрице А. третьего порядка вычеркиванием
третьего порядка вычеркиванием 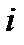 -й строки и
-й строки и  -го столбца, называется минором элемента
-го столбца, называется минором элемента 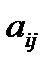 определителя
определителя  и обозначается
и обозначается  .
.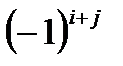 , обозначается
, обозначается 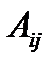 .
.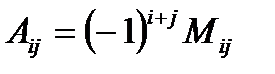 .
.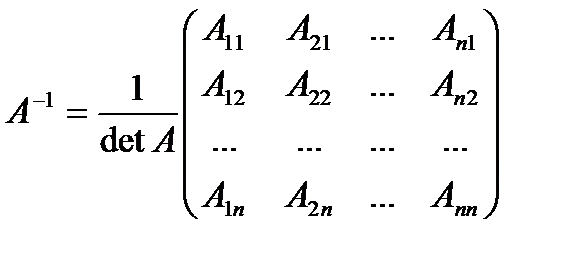 , где
, где
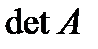 - определитель матрицы А,
- определитель матрицы А, 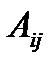 - алгебраические дополнения элементов матрицы А.
- алгебраические дополнения элементов матрицы А.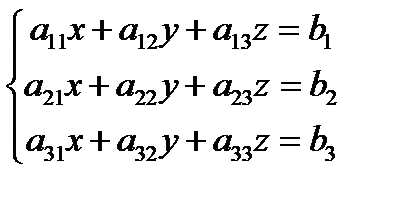
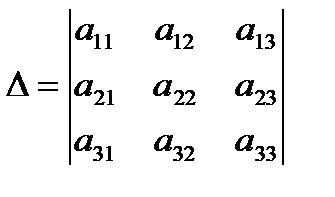 и дополнительные определители:
и дополнительные определители: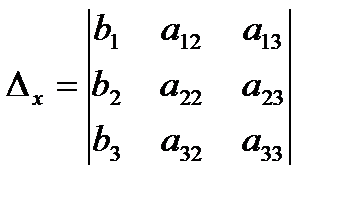 ,
, 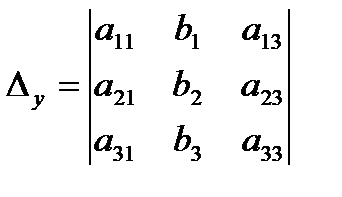 ,
, 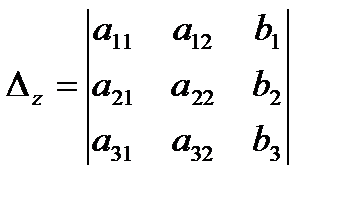 .
.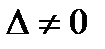 , то система имеет единственное решение, определяемое формулами Крамера:
, то система имеет единственное решение, определяемое формулами Крамера: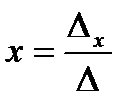 ,
,  ,
,  .
. . Ненулевые решения она имеет тогда и только тогда, когда
. Ненулевые решения она имеет тогда и только тогда, когда 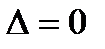 .
.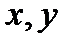 описывает некоторою прямую на плоскости.
описывает некоторою прямую на плоскости.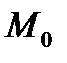 с известными координатами
с известными координатами 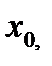 ,
, 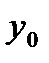 параллельно направляющему вектору
параллельно направляющему вектору 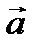 , координаты которого также известны и равны (
, координаты которого также известны и равны (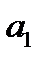 ,
, 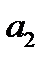 ).
).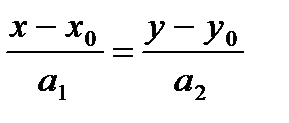 .
.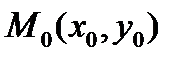 и имеющей данный направляющий вектор
и имеющей данный направляющий вектор 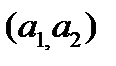 :
: 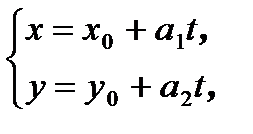
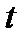 - параметр, принимающий все действительные значения.
- параметр, принимающий все действительные значения.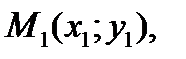
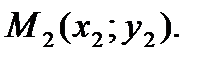 . Уравнение этой прямой имеет вид:
. Уравнение этой прямой имеет вид: 
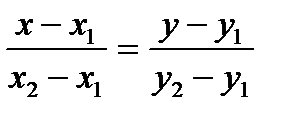 .
.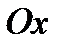 отрезок величины
отрезок величины 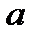 , на оси
, на оси 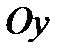 – отрезок
– отрезок 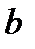 . В этом случае уравнение прямой будет иметь вид:
. В этом случае уравнение прямой будет иметь вид: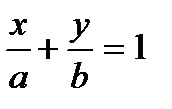 .
.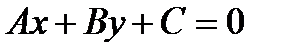 вычисляется по формуле
вычисляется по формуле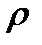 (
(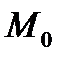 ,
, 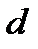 )=
)= 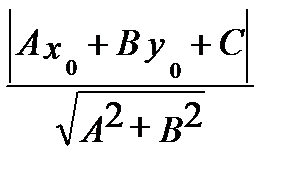 .
.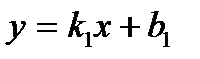 и
и 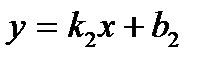 , вычисляется по формуле
, вычисляется по формуле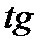
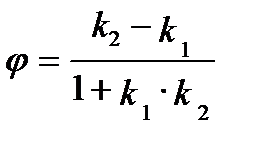 ,
,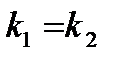 , а условие перпендикулярности
, а условие перпендикулярности 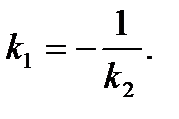
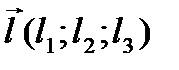 ,
, 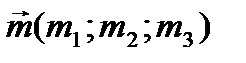 , параллельные этой плоскости.
, параллельные этой плоскости.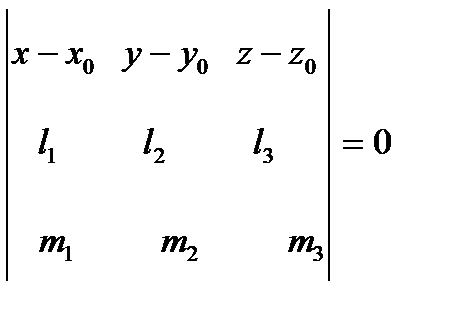
 , определяется или параметрическими уравнениями:
, определяется или параметрическими уравнениями: 1 t,
1 t, .
.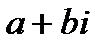 , где
, где 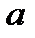 и
и 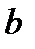 - действительные числа, а
- действительные числа, а 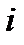 - комплексная единица, которая удовлетворяет условию
- комплексная единица, которая удовлетворяет условию 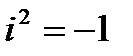 .
.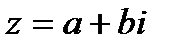 - алгебраическая форма записи комплексного числа,
- алгебраическая форма записи комплексного числа, 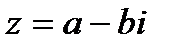 - комплексно-сопряженное число.
- комплексно-сопряженное число.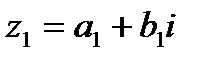 и
и 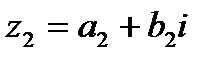 , тогда:
, тогда: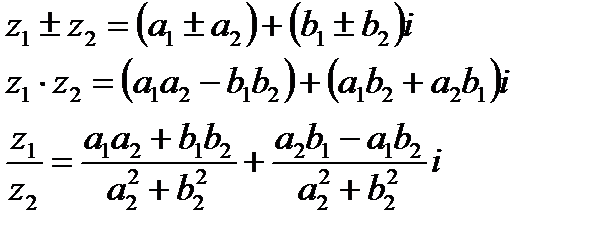
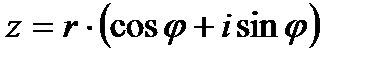 ,
,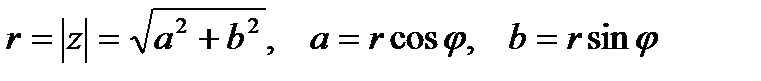 , при
, при 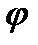 можно найти, используя формулу
можно найти, используя формулу 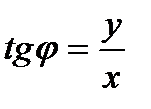 :
: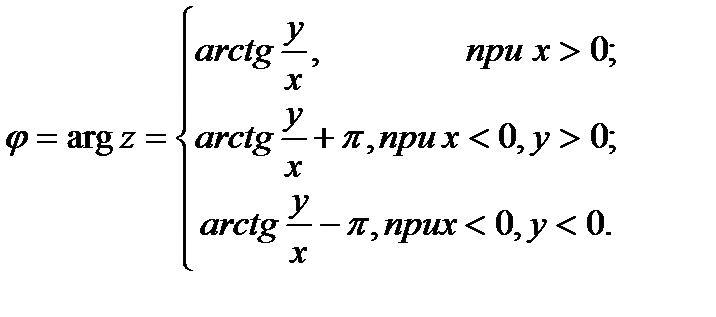
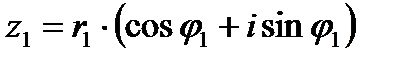 ,
, 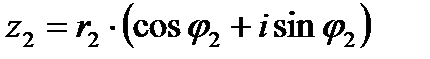 , тогда:
, тогда: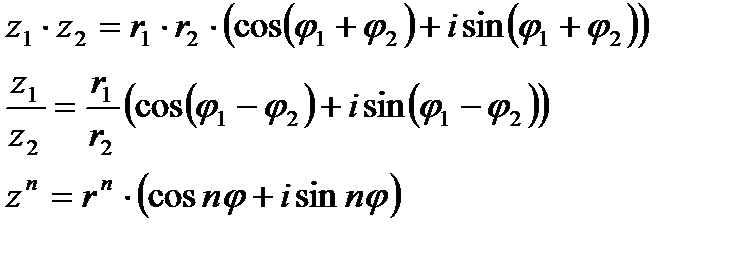
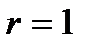 получаем формулу Муавра:
получаем формулу Муавра: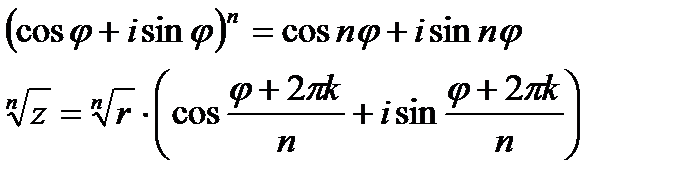 , где
, где 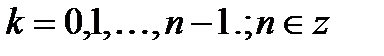 .
.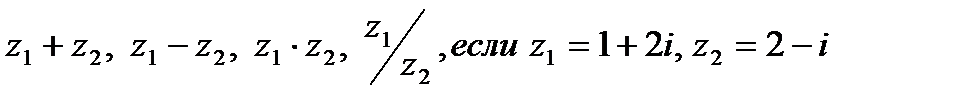

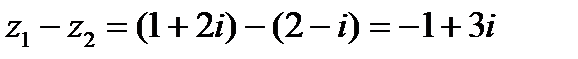
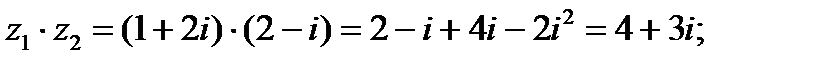
 .
.


