Частные производные.
Пусть z=f(x,y). Зафиксируем какую-либо точку (x,y), а затем, не меняя закрепленного значения аргумента y, придадим аргументу x приращение  . Тогда z получит приращение, которое называется частным приращением z по x и обозначается
. Тогда z получит приращение, которое называется частным приращением z по x и обозначается  и определяется формулой
и определяется формулой  .
.
Аналогично, если x сохраняет постоянное значение, а y получает приращение  , то z получает частное приращение z по y,
, то z получает частное приращение z по y,  .
.
Определение. Частной производной по x от функции z=f(x,y) называется предел отношения частного приращения  по x к приращению
по x к приращению  при стремлении
при стремлении  к нулю, т.е.
к нулю, т.е. 
Частная производная обозначается одним из символов  .
.
Таким образом, частные производные функции двух переменных вычисляются по тем же правилам, что и производные функции одного переменного.
Производные высших порядков
Если функция  имеет производную в каждой точке
имеет производную в каждой точке  своей области определения, то ее производная
своей области определения, то ее производная  есть функция от
есть функция от  . Функция
. Функция  , в свою очередь, может иметь производную, которую называют производной второго порядка функции
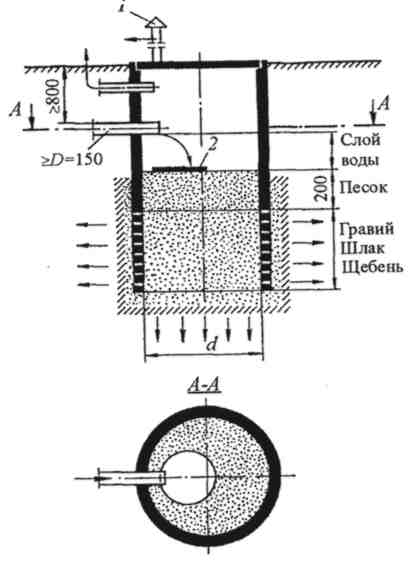
, в свою очередь, может иметь производную, которую называют производной второго порядка функции  (или второй производной) и обозначают символом
(или второй производной) и обозначают символом  . Таким образом
. Таким образом
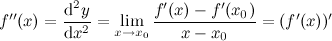
Производные более высоких порядков определяются аналогично. То есть производная  -го порядка функции
-го порядка функции 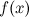 есть первая производная от производной
есть первая производная от производной  -го порядка этой функции:
-го порядка этой функции:

Значение частной производной dx\dz в точке P(x0;y0) равно тангенсу угла, составленного с осью Ox касательной, проведенной в точке M0(x0;y0;z0) к линии пересечения поверхности z=f(x,y) и плоскости у=y0. В этом заключается геометрический смысл частной производной.
1. Дифференциал функции двух переменных. Касательная плоскость и нормаль к поверхности. Определение экстремума функции. Необходимые и достаточные условия экстремума функции двух переменных
Пусть функция z =ƒ (х; у) определена в некоторой окрестности точки М(х;у). Составим полное приращение функции в точке М:
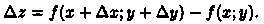
Функция z = ƒ (х; у) называется дифференцируемой в точке М(х; у), если ее полное приращение в этой точке можно представить в виде

где а = а(Δх, Δу)→0 и β=β(Δх,Δу)→0 при Δх→0, Δу→0. Сумма первых двух слагаемых в равенстве представляет собой главную часть приращения функции.
Главная часть приращение функции z=ƒ(х;у), линейная относительно Δх и Δу, называется полным дифференциалом этой функции и обозначается символом dz:
dz=A*Δx+B*Δy
ВыраженияА•Δх и В•Δу называют частными дифференциалами. Для независимых переменных х и у полагают Δх=dx и Δу=dy. Поэтому равенство (44.2) можно переписать в виде
dz=Adx+Bdy.
Говорят, что функция  имеет максимум в точке
имеет максимум в точке  , т.е. при
, т.е. при 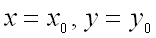 , если
, если 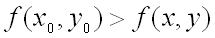 для всех точек
для всех точек  , достаточно близких к точке
, достаточно близких к точке  и отличных от неё.
и отличных от неё.
Говорят, что функция  имеет минимум в точке
имеет минимум в точке  , т.е. при
, т.е. при 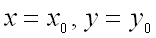 , если
, если  для всех точек
для всех точек  , достаточно близких к точке
, достаточно близких к точке  и отличных от неё.
и отличных от неё.
Максимум и минимум функции называются экстремумами функции.
Теорема (необходимое условие экстремума функции двух переменных). Если функция  достигает экстремума при
достигает экстремума при 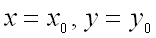 , то каждая частная производная первого порядка от
, то каждая частная производная первого порядка от  или обращается в нуль при этих значениях аргументов, или не существует.
или обращается в нуль при этих значениях аргументов, или не существует.
Теорема (достаточное условие экстремума функции двух переменных). Пусть в некоторой области, содержащей точку  функция
функция  имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того, точка
имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того, точка  является критической точкой функции
является критической точкой функции  , т.е.
, т.е.
 ,
,
тогда при 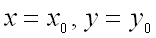 :
:
1)  имеет максимум, если дискриминант
имеет максимум, если дискриминант 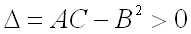 и
и  , где
, где  ;
;
2)  имеет минимум, если дискриминант
имеет минимум, если дискриминант 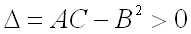 и
и  ;
;
3)  не имеет ни минимума, ни максимума, если дискриминант
не имеет ни минимума, ни максимума, если дискриминант  ;
;
4) если  , то экстремум может быть, а может и не быть (требуется дополнительное исследование).
, то экстремум может быть, а может и не быть (требуется дополнительное исследование).
Нормалью к поверхности в некоторой ее точке называется прямая, направляющий вектор которой является нормальным к поверхности в этой точке и которая проходит через эту точку.
Канонические уравнения нормали можно представить в виде
| | | x − x 0
| | F ' x (x 0, y 0, z 0)
| =
| y − y 0
| | F ' y (x 0, y 0, z 0)
| =
| z − z 0
| | F ' z (x 0, y 0, z 0)
| .
| | (2)
|
Касательной плоскостью к поверхности в некоторой точке называется плоскость, которая проходит через эту точку перпендикулярно нормали к поверхности в этой точке.
Из этого определения следует, что уравнение касательной плоскости имеет вид:
| | | F ' x (x 0, y 0, z 0) · (x − x 0) + F ' y (x 0, y 0, z 0) · (y − y 0) + F ' z (x 0, y 0, z 0) · (z − z 0) = 0.
| |
2. Двойной интеграл. Свойства. Вычисление. Правильные и неправильные области. Правильные области по ОХ и ОУ. Двукратный интеграл
Определение:
Двойным интегралом от функции 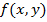 по ограниченной замкнутой области
по ограниченной замкнутой области  называется предел интегральной суммы, построенной для функции
называется предел интегральной суммы, построенной для функции 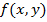 при неограниченном увеличении числа разбиений области
при неограниченном увеличении числа разбиений области  на ячейки (
на ячейки (  ) и пристягивание каждой ячейки в точку (
) и пристягивание каждой ячейки в точку ( 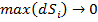 ), если такой предел существует и не зависит от способа разбиения области
), если такой предел существует и не зависит от способа разбиения области  на ячейки, ни от выбора
на ячейки, ни от выбора  в каждой из них.
в каждой из них.
Теорема существования:
Для всякой непрерывной функции 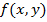 в ограниченной замкнутой области
в ограниченной замкнутой области  существует двойной интеграл:
существует двойной интеграл: 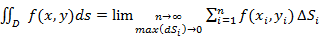
Свойства двойного интеграла:


3) Если область  разбить линией на две области
разбить линией на две области  и
и  такие, что
такие, что  , а пересечение
, а пересечение  и
и  состоит лишь из линии, их разделяющей, то:
состоит лишь из линии, их разделяющей, то:

4) Если в области  имеет место неравенство
имеет место неравенство  , то и
, то и  . Если в области
. Если в области  функции
функции  и
и 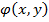 удовлетворяют неравенству, то и
удовлетворяют неравенству, то и 

6) Если функция  непрерывна в замкнутой области
непрерывна в замкнутой области  , площадь которой
, площадь которой  , то
, то  , где
, где 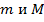 – соответственно наименьшее и наибольшее значения подынтегральной функции в области
– соответственно наименьшее и наибольшее значения подынтегральной функции в области  .
.
7) Если функция непрерывна в замкнутой области  , площадь которой
, площадь которой  , то в этой области существует такая точка
, то в этой области существует такая точка  , что
, что  . Величину
. Величину  называют средним значением функции
называют средним значением функции  в области
в области 
Назовем область D правильной в отношении оси Ох, если она ограничена:
сверху — графиком только одной функции

снизу — графиком только одной функции
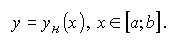
При этом все "угловые" точки области при проектировании на ось Ох дают только две проекции.
Назовем область Dправильной в отношении оси Оу, если количество проекций всех "угловых" точек области D на ось Оу равно двум.
Если количество этих проекций больше двух, то область D называется неправильной в отношении оси Оу.
Область D называется неправильной, если она не является правильной ни в отношении оси Ох, ни в отношении оси Оу.
Теорема. Двойной интеграл от непрерывной функции f(x,y) по области Dравен двукратному интегралу по этой же области.
4)Тройной интеграл свойства, определение.
Определение правильной области,
Трехкратный интеграл. Вычисление трехкратного интеграла.
Пусть f(x; y; z), (x; y; z)  U – произвольная функция трех переменных, U – ограниченная трехмерная область
U – произвольная функция трех переменных, U – ограниченная трехмерная область
Разобьем U произвольным образом на части ΔU1, ΔU2,..., ΔUn. В каждой из них возьмем произвольную точку Mi(xi;yi;zi)  Ui и составим интегральную сумму:
Ui и составим интегральную сумму:

Если существует предел интегральной суммы:
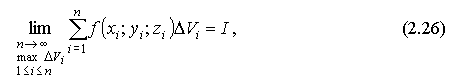
не зависящий от способа разбиения U на n частей ΔU1, ΔU2,..., ΔUn, а также от произвола в выборе точек Mi  Ui, то этот предел I обозначается через
Ui, то этот предел I обозначается через 
и называется тройным интегралом от функции f(x; y; z) по объёму U. При этом функция f(x; y; z) называется интегрируемой по U.
Тройные интегралы от непрерывных функций называются собственными тройными интегралами (или просто тройными интегралами), а тройные интегралы от разрывных функций – несобственными тройными интегралами.



5)Определение дифференциального уравнения. Определение порядка дифференциального уравнения. Определение решения дифференциального уравнения. Общее решение дифференциального уравнения. Частное решение дифференциального уравнения. Дифференциальное уравнение с разделяющими переменными. Однородные дифференциальные уравнения первого порядка. Определение однородной функции. Решение однородного дифференциального уравнения.
Дифференциальное уравнение (ДУ) – это уравнение, в которое входит неизвестная функция под знаком производной или дифференциала.
Если неизвестная функция является функцией одной переменной, то дифференциальное уравнение называют обыкновенным (сокращенно ОДУ – обыкновенное дифференциальное уравнение). Если же неизвестная функция есть функция многих переменных, то дифференциальное уравнение называют уравнением в частных производных.
Максимальный порядок производной неизвестной функции, входящей в дифференциальное уравнение, называется порядком дифференциального уравнения.
Решение дифференциального уравнения - это неявно заданная функция Ф(x, y) = 0 (в некоторых случаях функцию y можно выразить через аргумент x явно), которая обращает дифференциальное уравнение в тождество.
Общее решение дифференциального уравнения – это множество решений, содержащее все без исключения решения этого дифференциального уравнения.
Общее решение дифференциального уравнения еще называют общим интегралом дифференциального уравнения.
Если решение дифференциального уравнения удовлетворяет изначально заданным дополнительным условиям, то его называют частным решением дифференциального уравнения.
Уравнение вида  , в котором коэффициенты при дифференциалах распадаются на множители, зависящие только от
, в котором коэффициенты при дифференциалах распадаются на множители, зависящие только от  и только от
и только от  , называется уравнением с разделяющимися переменными.
, называется уравнением с разделяющимися переменными.
Путем деления на произведение  оно приводится к уравнению с разделенными переменными:
оно приводится к уравнению с разделенными переменными:

Дифференциальное уравнение вида

где  и
и  — постоянные, заменой переменных
— постоянные, заменой переменных  преобразуется в уравнение с разделяющимися переменными.
преобразуется в уравнение с разделяющимися переменными.
Структура общего решения
Линейное неоднородное уравнение данного типа имеет вид:
 где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение:
где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение:

Теорема: Общее решение неоднородного уравнения является суммой общего решения y 0(x)соответствуюшего однородного уравнения и частного решения y 1(x) неоднородного уравнения: 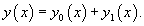
Ниже мы рассмотрим два способа решения неоднородных дифференциальных уравнений.
Метод вариации постоянных
Если общее решение y 0 ассоциированного однородного уравнения известно, то общее решение неоднородного уравнения можно найти, используя метод вариации постоянных.
Пусть общее решение однородного дифференциального уравнения второго порядка имеет вид:  Вместо постоянных C 1 и C 2 будем рассматривать вспомогательные функции C 1(x) и C 2(x). Будем искать эти функции такими, чтобы решение удовлетворяло неоднородному уравнению с правой частью f (x).
Вместо постоянных C 1 и C 2 будем рассматривать вспомогательные функции C 1(x) и C 2(x). Будем искать эти функции такими, чтобы решение удовлетворяло неоднородному уравнению с правой частью f (x).

Неизвестные функции C 1(x) и C 2(x) определяются из системы двух уравнений:

Принцип суперпозиции
Если правая часть неоднородного уравнения представляет собой сумму нескольких функций вида
 то частное решение дифференциального уравнения также будет являться суммой частных решений, построенных отдельно для каждого слагаемого в правой части.
то частное решение дифференциального уравнения также будет являться суммой частных решений, построенных отдельно для каждого слагаемого в правой части.
Пример 1
Решить дифференциальное уравнение y'' + y = sin(2 x).
Решение.
Сначала мы решим соответствующее однородное уравнение y'' + y = 0. В данном случае корни характеристического уравнения являтся чисто мнимыми:

Следовательно, общее решение однородного уравнения определяется выражением
 Вернемся снова к неоднородному уравнению. Будем искать его решение в виде
Вернемся снова к неоднородному уравнению. Будем искать его решение в виде
 используя метод вариации постояных.
используя метод вариации постояных.
Функции C 1(x) и C 2(x) можно найти из следующей системы уравнений:
 Тогда
Тогда

Выразим производную C 1 ' (x) из первого уравнения:
 Подставляя во второе уравнение, находим производную C 2 ' (x):
Подставляя во второе уравнение, находим производную C 2 ' (x):

Интегрируя выражения для производных C 1 ' (x) и C 2 ' (x), получаем:
 где A 1, A 2 − постоянные интегрирования.
где A 1, A 2 − постоянные интегрирования.
Теперь подставим найденные функции C 1(x) и C 2(x) в формулу для y 1(x) и запишем общее решениенеоднородного уравнения:

8) Определение решения линейного неоднороддиффурав-ния.
Подбора

Т.Общее решение лин.неоднородногоур-ния может быть представлено как сумма двух решений.
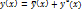 где
где  -общее решение,
-общее решение,  -к-либо частное решение неоднородн.ур-ния.
-к-либо частное решение неоднородн.ур-ния.
Пусть  есть решения соответств. однородного ур-ния:
есть решения соответств. однородного ур-ния: 
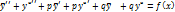
 (скобка =0).
(скобка =0).


 ;
;

 - общее решение для любых началных условий
- общее решение для любых началных условий
Метод подбора.

 ,
,  если
если 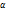 не есть корень характеристического ур-ния
не есть корень характеристического ур-ния


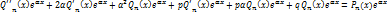 (сокращаем на
(сокращаем на 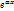 )
)

Если  тогда
тогда 
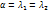 =>
=> 
Пример. 



 -общ.решение.
-общ.решение.
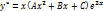


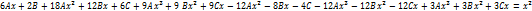


Определения и методы решения

Определение 1. Уравнение вида:
 (1)
(1)
где  и
и  – заданные непрерывные функции на
– заданные непрерывные функции на 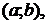 называется линейным дифференциальным уравнением (ЛДУ). Если
называется линейным дифференциальным уравнением (ЛДУ). Если  при
при  то уравнение имеет вид:
то уравнение имеет вид:

и называется линейным однородным дифференциальным уравнением (ЛОДУ). А если  при
при  то уравнение (1) называется линейным неоднородным дифференциальным уравнением (ЛНДУ).
то уравнение (1) называется линейным неоднородным дифференциальным уравнением (ЛНДУ).
Метод решения ЛНДУ
1) Метод вариации произвольной постоянной:
· сначала решить соответствующее ЛОДУ, которое является уравнением с разделяющимися переменными:


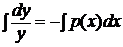


 (2)
(2)
· заменить в формуле (2) постоянную  на неизвестную функцию
на неизвестную функцию  и подставить это выражение вместо
и подставить это выражение вместо  в уравнение (1), предварительно найдя
в уравнение (1), предварительно найдя 
· из полученного уравнения найти функцию 
· записать ответ:

где  произвольная постоянная.
произвольная постоянная.
2) Метод Бернулли:
· выполнить в уравнении (1) замену Бернулли:


 (3)
(3)
· приравнять к нулю выражение

и найти отсюда любое частное решение 


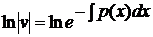

· подставить полученную функцию  в уравнение (3) и найти общее решение
в уравнение (3) и найти общее решение  из этого уравнения;
из этого уравнения;
· записать ответ: 
где  произвольная постоянная.
произвольная постоянная.
Уравнение Бернулли
Определение 2. Уравнение вида
 где
где  и
и  (4)
(4)
называется уравнением Бернулли с показателем  .
.
Уравнение (4) приводится к ЛНДУ(1) с помощью замены:

После этой замены уравнение (1) приводится к следующему:

Это уравнение ЛНДУ относительно функции  Его можно решать также с помощью замены Бернулли. Но можно и уравнение (4), не проводя замену к функции
Его можно решать также с помощью замены Бернулли. Но можно и уравнение (4), не проводя замену к функции  , решать методом замены Бернулли непосредственно. При этом функция
, решать методом замены Бернулли непосредственно. При этом функция  будет частным решением уравнения
будет частным решением уравнения

а функция  будет находиться из уравнения
будет находиться из уравнения
 .
.
Замечание 1. При таком решении при  решение
решение  будет всегда потеряно.
будет всегда потеряно.
Замечание 2. Некоторые дифференциальные уравнения первого порядка становятся линейными или уравнениями Бернулли, если в них поменять ролями искомую функцию  и независимую переменную
и независимую переменную  .
.
Неоднородная система дифференциальных уравнений, которая в большинстве случаев может встретиться вам в задачах, имеет следующий вид:
Частным случаем канонической системы дифференциальных уравнений является одно уравнение n-го порядка, разрешенное относительно старшей производной.

Введением новых функций

это уравнение заменяется нормальной системой  уравнений
уравнений
Можно утверждать и обратное, что, вообще говоря, нормальная система  уравнений первого порядка
уравнений первого порядка
эквивалентна одному уравнению порядка  . На этом основан один из методов интегрирования систем дифференциальных уравнений — метод исключения.
. На этом основан один из методов интегрирования систем дифференциальных уравнений — метод исключения.
Проиллюстрируем этот метод на примере системы двух уравнений:

Здесь  — постоянные коэффициенты, а
— постоянные коэффициенты, а  и
и  — заданные функции;
— заданные функции;  и
и  — искомые функции. Из первого уравнения системы (1) находим
— искомые функции. Из первого уравнения системы (1) находим

Подставляя во второе уравнение системы вместо у правую часть (2), а вместо  производную от правой части (2), получаем уравнение at второго порядка относительно
производную от правой части (2), получаем уравнение at второго порядка относительно 

где  — постоянные. Отсюда находим
— постоянные. Отсюда находим  . Подставив найденное выражение для
. Подставив найденное выражение для  и
и  в (2), найдем
в (2), найдем  .
.
10. Числовые ряды. Опред сходимости числового ряда. Сумма, остаточный член числового ряда. Признаки сходимости: Признак Даламбера, радикальный и интегральный признаки сходимости Коши.
Числовой ряд – это сумма членов числовой последовательности вида  .
.
В качестве примера числового ряда можно привести сумму бесконечно убывающей геометрической прогрессии со знаменателем q = -0.5:  .
.
 называют общим членом числового ряда или k–ым членом ряда.
называют общим членом числового ряда или k–ым членом ряда.
Для предыдущего примера общий член числового ряда имеет вид  .
.
Частичная сумма числового ряда – это сумма вида  , где n – некоторое натуральное число.
, где n – некоторое натуральное число.  называют также n-ой частичной суммой числового ряда.
называют также n-ой частичной суммой числового ряда.
К примеру, четвертая частичная сумма ряда  есть
есть  .
.
Частичные суммы  образуют бесконечную последовательность частичных сумм числового ряда.
образуют бесконечную последовательность частичных сумм числового ряда.
Для нашего ряда n –ая частичная сумма находится по формуле суммы первых n членов геометрической прогрессии  , то есть, будем иметь следующую последовательность частичных сумм:
, то есть, будем иметь следующую последовательность частичных сумм:  .
.
Числовой ряд  называется сходящимся, если существует конечный предел последовательности частичных сумм
называется сходящимся, если существует конечный предел последовательности частичных сумм  . Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд
. Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд  называется расходящимся.
называется расходящимся.
Суммой сходящегося числового ряда  называется предел последовательности его частичных сумм, то есть,
называется предел последовательности его частичных сумм, то есть,  .
.
Признак Даламбера.
Пусть  - знакоположительный числовой ряд. Если
- знакоположительный числовой ряд. Если  , то числовой ряд сходится, если
, то числовой ряд сходится, если  , то ряд расходится.
, то ряд расходится.
Замечание.
Признак Даламбера справедлив, если предел бесконечен, то есть, если  , то ряд сходится, если
, то ряд сходится, если  , то ряд расходится.
, то ряд расходится.
Если  , то признак Даламбера не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.
, то признак Даламбера не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.
Радикальный признак Коши.
Пусть  - знакоположительный числовой ряд. Если
- знакоположительный числовой ряд. Если  , то числовой ряд сходится, если
, то числовой ряд сходится, если  , то ряд расходится.
, то ряд расходится.
Замечание.
Радикальный признак Коши справедлив, если предел бесконечен, то есть, если  , то ряд сходится, если
, то ряд сходится, если 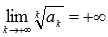 , то ряд расходится.
, то ряд расходится.
Если  , то радикальный признак Коши не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.
, то радикальный признак Коши не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.
Обычно достаточно легко разглядеть случаи, когда лучше всего использовать радикальный признак Коши. Характерным является случай, когда общий член числового ряда представляет собой показательно степенное выражение.
Интегральный признак Коши.
Пусть  - знакоположительный числовой ряд. Составим функцию непрерывного аргумента y = f(x), аналогичную функции
- знакоположительный числовой ряд. Составим функцию непрерывного аргумента y = f(x), аналогичную функции  . Пусть функция y = f(x) положительная, непрерывная и убывающая на интервале
. Пусть функция y = f(x) положительная, непрерывная и убывающая на интервале  , где
, где 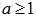 ). Тогда в случае сходимости несобственного интеграла
). Тогда в случае сходимости несобственного интеграла  сходится исследуемый числовой ряд. Если же несобственный интеграл расходится, то исходный ряд тоже расходится.
сходится исследуемый числовой ряд. Если же несобственный интеграл расходится, то исходный ряд тоже расходится.
При проверке убывания функции y = f(x) на интервале  Вам может пригодится теория из раздела возрастание и убывание функции.
Вам может пригодится теория из раздела возрастание и убывание функции.
11. Функциональные ряды. Область сходимости функционального ряда. Степенные ряды. Теорема Абеля. Равенство сходимости методом Даламбера и Коши
Функциональный же ряд состоит из ФУНКЦИЙ:

В общий член ряда 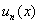 помимо многочленов, факториалов и других подарков непременно входит буковка «икс». Выглядит это, например, так:
помимо многочленов, факториалов и других подарков непременно входит буковка «икс». Выглядит это, например, так:  . Как и числовой ряд, любой функциональный ряд можно расписать в развернутом виде:
. Как и числовой ряд, любой функциональный ряд можно расписать в развернутом виде:

Как видите, все члены функционального ряда  – это функции.
– это функции.
Наиболее популярной разновидностью функционального ряда является степенной ряд.
Совокупность тех значений х при которых данный ряд сходится называется областью сходимости функционального ряда. Функциональный ряд сходится если, предел от остаточного члена ряда при n->∞равен 0.
Степенной ряд – это ряд, в общий член 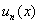 которого входят целые положительные степени независимой переменной
которого входят целые положительные степени независимой переменной  . Упрощенно степенной ряд во многих учебниках записывают так:
. Упрощенно степенной ряд во многих учебниках записывают так:  , где
, где  – это старая знакомая «начинка» числовых рядов (многочлены, степени, факториалы, зависящие только от «эн»). Простейший пример:
– это старая знакомая «начинка» числовых рядов (многочлены, степени, факториалы, зависящие только от «эн»). Простейший пример:

Теорема Н. Абеля.
Если степенной ряд  сходится в точке
сходится в точке  , то он сходится и в любой точке
, то он сходится и в любой точке  , расположенной ближе к центру
, расположенной ближе к центру  , чем
, чем  , причем в любой сфере
, причем в любой сфере  , где
, где  , сходимость ряда равномерна.
, сходимость ряда равномерна.
12. Ряды Тейлора и Макларена. Разложение элементарных функций в ряд Макларена
Если функция f (x) имеет непрерывные производные вплоть до (n+ 1)-го порядка, то ее мо


 . Тогда z получит приращение, которое называется частным приращением z по x и обозначается
. Тогда z получит приращение, которое называется частным приращением z по x и обозначается  и определяется формулой
и определяется формулой  .
. , то z получает частное приращение z по y,
, то z получает частное приращение z по y,  .
. по x к приращению
по x к приращению 
 .
. имеет производную в каждой точке
имеет производную в каждой точке  своей области определения, то ее производная
своей области определения, то ее производная  есть функция от
есть функция от  , в свою очередь, может иметь производную, которую называют производной второго порядка функции
, в свою очередь, может иметь производную, которую называют производной второго порядка функции  . Таким образом
. Таким образом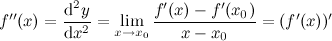
 -го порядка функции
-го порядка функции  есть первая производная от производной
есть первая производная от производной  -го порядка этой функции:
-го порядка этой функции:
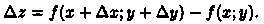

 имеет максимум в точке
имеет максимум в точке  , т.е. при
, т.е. при 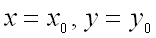 , если
, если 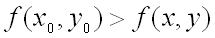 для всех точек
для всех точек  , достаточно близких к точке
, достаточно близких к точке  и отличных от неё.
и отличных от неё. для всех точек
для всех точек  или обращается в нуль при этих значениях аргументов, или не существует.
или обращается в нуль при этих значениях аргументов, или не существует. , т.е.
, т.е. ,
,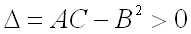 и
и  , где
, где  ;
; ;
; ;
; , то экстремум может быть, а может и не быть (требуется дополнительное исследование).
, то экстремум может быть, а может и не быть (требуется дополнительное исследование).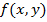 по ограниченной замкнутой области
по ограниченной замкнутой области  называется предел интегральной суммы, построенной для функции
называется предел интегральной суммы, построенной для функции  на ячейки (
на ячейки (  ) и пристягивание каждой ячейки в точку (
) и пристягивание каждой ячейки в точку ( 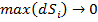 ), если такой предел существует и не зависит от способа разбиения области
), если такой предел существует и не зависит от способа разбиения области  в каждой из них.
в каждой из них.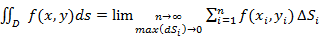


 и
и  такие, что
такие, что  , а пересечение
, а пересечение 
 , то и
, то и  . Если в области
. Если в области  и
и  удовлетворяют неравенству, то и
удовлетворяют неравенству, то и 

 , то
, то  , где
, где  – соответственно наименьшее и наибольшее значения подынтегральной функции в области
– соответственно наименьшее и наибольшее значения подынтегральной функции в области  , что
, что  . Величину
. Величину  называют средним значением функции
называют средним значением функции  в области
в области 

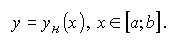
 U – произвольная функция трех переменных, U – ограниченная трехмерная область
U – произвольная функция трех переменных, U – ограниченная трехмерная область
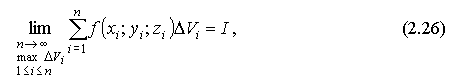




 , в котором коэффициенты при дифференциалах распадаются на множители, зависящие только от
, в котором коэффициенты при дифференциалах распадаются на множители, зависящие только от  и только от
и только от  , называется уравнением с разделяющимися переменными.
, называется уравнением с разделяющимися переменными. оно приводится к уравнению с разделенными переменными:
оно приводится к уравнению с разделенными переменными:

 и
и  — постоянные, заменой переменных
— постоянные, заменой переменных  преобразуется в уравнение с разделяющимися переменными.
преобразуется в уравнение с разделяющимися переменными. где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение:
где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение:
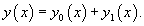
 Вместо постоянных C 1 и C 2 будем рассматривать вспомогательные функции C 1(x) и C 2(x). Будем искать эти функции такими, чтобы решение удовлетворяло неоднородному уравнению с правой частью f (x).
Вместо постоянных C 1 и C 2 будем рассматривать вспомогательные функции C 1(x) и C 2(x). Будем искать эти функции такими, чтобы решение удовлетворяло неоднородному уравнению с правой частью f (x).

 то частное решение дифференциального уравнения также будет являться суммой частных решений, построенных отдельно для каждого слагаемого в правой части.
то частное решение дифференциального уравнения также будет являться суммой частных решений, построенных отдельно для каждого слагаемого в правой части.
 Вернемся снова к неоднородному уравнению. Будем искать его решение в виде
Вернемся снова к неоднородному уравнению. Будем искать его решение в виде используя метод вариации постояных.
используя метод вариации постояных. Тогда
Тогда
 Подставляя во второе уравнение, находим производную C 2 ' (x):
Подставляя во второе уравнение, находим производную C 2 ' (x):
 где A 1, A 2 − постоянные интегрирования.
где A 1, A 2 − постоянные интегрирования.

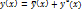 где
где  -общее решение,
-общее решение,  -к-либо частное решение неоднородн.ур-ния.
-к-либо частное решение неоднородн.ур-ния. есть решения соответств. однородного ур-ния:
есть решения соответств. однородного ур-ния: 
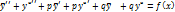
 (скобка =0).
(скобка =0).

 ;
;
 - общее решение для любых началных условий
- общее решение для любых началных условий
 ,
,  если
если 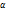 не есть корень характеристического ур-ния
не есть корень характеристического ур-ния

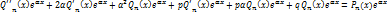 (сокращаем на
(сокращаем на 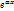 )
)
 тогда
тогда 
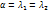 =>
=> 




 -общ.решение.
-общ.решение.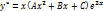


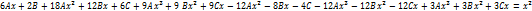



 (1)
(1) и
и  – заданные непрерывные функции на
– заданные непрерывные функции на 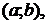 называется линейным дифференциальным уравнением (ЛДУ). Если
называется линейным дифференциальным уравнением (ЛДУ). Если  при
при  то уравнение имеет вид:
то уравнение имеет вид:
 при
при 
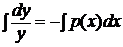


 (2)
(2) на неизвестную функцию
на неизвестную функцию  и подставить это выражение вместо
и подставить это выражение вместо  в уравнение (1), предварительно найдя
в уравнение (1), предварительно найдя 


 произвольная постоянная.
произвольная постоянная.

 (3)
(3)



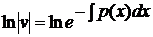

 в уравнение (3) и найти общее решение
в уравнение (3) и найти общее решение  из этого уравнения;
из этого уравнения;
 произвольная постоянная.
произвольная постоянная. где
где  и
и  (4)
(4) .
.

 Его можно решать также с помощью замены Бернулли. Но можно и уравнение (4), не проводя замену к функции
Его можно решать также с помощью замены Бернулли. Но можно и уравнение (4), не проводя замену к функции  , решать методом замены Бернулли непосредственно. При этом функция
, решать методом замены Бернулли непосредственно. При этом функция  будет частным решением уравнения
будет частным решением уравнения
 .
. решение
решение  будет всегда потеряно.
будет всегда потеряно. .
.

 уравнений
уравнений
 — постоянные коэффициенты, а
— постоянные коэффициенты, а  и
и  — заданные функции;
— заданные функции;  и
и  — искомые функции. Из первого уравнения системы (1) находим
— искомые функции. Из первого уравнения системы (1) находим
 производную от правой части (2), получаем уравнение at второго порядка относительно
производную от правой части (2), получаем уравнение at второго порядка относительно 
 — постоянные. Отсюда находим
— постоянные. Отсюда находим  . Подставив найденное выражение для
. Подставив найденное выражение для  в (2), найдем
в (2), найдем  .
. .
. называют общим членом числового ряда или k–ым членом ряда.
называют общим членом числового ряда или k–ым членом ряда. .
. , где n – некоторое натуральное число.
, где n – некоторое натуральное число.  называют также n-ой частичной суммой числового ряда.
называют также n-ой частичной суммой числового ряда. есть
есть  .
. образуют бесконечную последовательность частичных сумм числового ряда.
образуют бесконечную последовательность частичных сумм числового ряда. , то есть, будем иметь следующую последовательность частичных сумм:
, то есть, будем иметь следующую последовательность частичных сумм:  .
. называется сходящимся, если существует конечный предел последовательности частичных сумм
называется сходящимся, если существует конечный предел последовательности частичных сумм  . Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд
. Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд  .
. , то числовой ряд сходится, если
, то числовой ряд сходится, если  , то ряд расходится.
, то ряд расходится. , то ряд сходится, если
, то ряд сходится, если  , то ряд расходится.
, то ряд расходится. , то признак Даламбера не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.
, то признак Даламбера не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование. , то числовой ряд сходится, если
, то числовой ряд сходится, если  , то ряд расходится.
, то ряд расходится. , то ряд сходится, если
, то ряд сходится, если 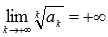 , то ряд расходится.
, то ряд расходится. , то радикальный признак Коши не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование.
, то радикальный признак Коши не дает информацию о сходимости или расходимости ряда и требуется дополнительное исследование. . Пусть функция y = f(x) положительная, непрерывная и убывающая на интервале
. Пусть функция y = f(x) положительная, непрерывная и убывающая на интервале  , где
, где 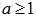 ). Тогда в случае сходимости несобственного интеграла
). Тогда в случае сходимости несобственного интеграла  сходится исследуемый числовой ряд. Если же несобственный интеграл расходится, то исходный ряд тоже расходится.
сходится исследуемый числовой ряд. Если же несобственный интеграл расходится, то исходный ряд тоже расходится.
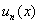 помимо многочленов, факториалов и других подарков непременно входит буковка «икс». Выглядит это, например, так:
помимо многочленов, факториалов и других подарков непременно входит буковка «икс». Выглядит это, например, так:  . Как и числовой ряд, любой функциональный ряд можно расписать в развернутом виде:
. Как и числовой ряд, любой функциональный ряд можно расписать в развернутом виде:
 – это функции.
– это функции. . Упрощенно степенной ряд во многих учебниках записывают так:
. Упрощенно степенной ряд во многих учебниках записывают так:  , где
, где  – это старая знакомая «начинка» числовых рядов (многочлены, степени, факториалы, зависящие только от «эн»). Простейший пример:
– это старая знакомая «начинка» числовых рядов (многочлены, степени, факториалы, зависящие только от «эн»). Простейший пример: 
 сходится в точке
сходится в точке  , то он сходится и в любой точке
, то он сходится и в любой точке  , расположенной ближе к центру
, расположенной ближе к центру  , чем
, чем  , где
, где  , сходимость ряда равномерна.
, сходимость ряда равномерна.