Вопросы к экзамену
по дисциплине “Математический анализ”
Тема 1: Введение в анализ
1. Функциональная зависимость и виды её представления (основные понятия, способы задания функций, свойства функций).
— математическое понятие, отражающее связь между элементами множеств. записывается  или
или  .
.
Функция может быть задана тремя основными способами: аналитически, таблично или графически.
Функция  , определенная на множестве D называется четной, если для любых значений
, определенная на множестве D называется четной, если для любых значений 
 . Функции возрастающие, убывающие, неубывающие, невозрастающие называются монотонными функциями. Функции возрастающие, убывающие, называются строго монотонными функциями. Функция
. Функции возрастающие, убывающие, неубывающие, невозрастающие называются монотонными функциями. Функции возрастающие, убывающие, называются строго монотонными функциями. Функция  , определенная на множестве
, определенная на множестве 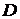 , называется периодической на этом множестве, если существует такое число
, называется периодической на этом множестве, если существует такое число 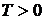 , что при любом
, что при любом  значение
значение 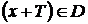 и
и 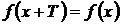 . При этом число
. При этом число 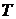 называется периодом функции.
называется периодом функции.
2. Классификация функций (простейшие элементарные функции, неявная, обратная и сложная функции, алгебраические и трансцендентные функции).
Функция называется явной, если она задана формулой, в которой правая часть не содержит зависимой переменной; например, функция у=х2 +5х + 1.Функция  аргумента
аргумента  называется неявной, если она задана уравнением
называется неявной, если она задана уравнением  , не разрешенным относительно зависимой переменной. Например, функция у(у>0), заданная уравнением х5 + у2 - х =0.
, не разрешенным относительно зависимой переменной. Например, функция у(у>0), заданная уравнением х5 + у2 - х =0.
Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными. К основным элементарным относятся следующие функции: степенная функция у=хα, α 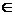 R; показательная функция у=ах, а › 0, а ≠1; логарифмическая функция y=logax, а › 0, а ≠1; тригонометрические формулы и обратные тригонометрические формулы. Алгебраической называется функция, в которой над аргументом проводится конечное число алгебраических действий.(целая рациональная функция, дробно-рациональная функция, иррациональная функция). Любая неалгебраическая функция называется трансцендентной. К числу трансцендентных функций относятся функции: показательная, логарифмическая, тригонометрические, обратные тригонометрические.
R; показательная функция у=ах, а › 0, а ≠1; логарифмическая функция y=logax, а › 0, а ≠1; тригонометрические формулы и обратные тригонометрические формулы. Алгебраической называется функция, в которой над аргументом проводится конечное число алгебраических действий.(целая рациональная функция, дробно-рациональная функция, иррациональная функция). Любая неалгебраическая функция называется трансцендентной. К числу трансцендентных функций относятся функции: показательная, логарифмическая, тригонометрические, обратные тригонометрические.
3. Преобразование графиков (все случаи с примером на графике).
Правило 1. Чтобы получить график функции  из графика функции
из графика функции  , нужно график функции
, нужно график функции  сдвинуть вдоль оси
сдвинуть вдоль оси 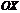 на
на  вправо, если
вправо, если  , или на
, или на  влево, если
влево, если 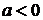 .
.
Правило 2. Чтобы получить график функции 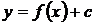 из графика функции
из графика функции  , нужно график функции
, нужно график функции  сдвинуть вдоль оси
сдвинуть вдоль оси  на
на  вверх, если
вверх, если  , или на
, или на  вниз, если
вниз, если  .
.
Правило 3. Чтобы получить график функции  из графика функции
из графика функции  , нужно график функции
, нужно график функции  зеркально отразить относительно оси
зеркально отразить относительно оси  .
.
Правило 4. Чтобы получить график функции  из графика функции
из графика функции  , нужно график функции
, нужно график функции  зеркально отразить относительно оси
зеркально отразить относительно оси 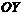 .
.
Правило 5. Чтобы построить график функции  , нужно значение ординаты графика функции
, нужно значение ординаты графика функции  умножить на число
умножить на число  , а абсциссу оставить без изменения.
, а абсциссу оставить без изменения.
Правило 6. Чтобы построить график функции  , нужно значение
, нужно значение  разделить на число
разделить на число  .
.
Правило 7. Чтобы получить график функции 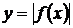 из графика функции
из графика функции  , надо участки графика функции
, надо участки графика функции  , лежащие выше оси
, лежащие выше оси  , оставить без изменения, а участки ниже оси
, оставить без изменения, а участки ниже оси 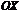 зеркально отразить относительно этой оси.
зеркально отразить относительно этой оси.
Правило 8. Чтобы получить график функции у= f(|х|) из графика функции  , надо построить график функции
, надо построить график функции  , при
, при  и отразить его зеркально относительно оси
и отразить его зеркально относительно оси 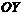 .
.
4. Предел числовой последовательности (понятие числовой последовательности, определение предела числовой последовательности, геометрический смысл предела числовой последовательности).
Числовая последовательность — это функция натурального аргумента: 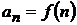 . Последовательность
. Последовательность 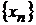 называется ограниченной сверху (снизу), если существует число
называется ограниченной сверху (снизу), если существует число  (число
(число  ) такое, что любой элемент
) такое, что любой элемент 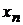 этой последовательности удовлетворяет неравенству
этой последовательности удовлетворяет неравенству  (
( ).
).
Число  называется пределом числовой последовательности
называется пределом числовой последовательности  , если для любого числа
, если для любого числа  , существует такой номер
, существует такой номер  , что для всех членов последовательности с номерами
, что для всех членов последовательности с номерами  выполняется неравенство
выполняется неравенство  .
.
Число a – предел последовательности xn, если в любую окрестность числа а, начиная с некоторого номера попадают все члены последовательности {xn}
5. Предел функции в точке (определение предела функции в точке, односторонние пределы, условие существования предела функции в точке, бесконечно большая последовательность определение предела функции на языке последовательностей, предел функции на бесконечности).
(по Коши). Число  называется пределом функции
называется пределом функции  при
при  , стремящимся к
, стремящимся к  (или в точке
(или в точке  ), если для любого, даже очень малого числа
), если для любого, даже очень малого числа  , найдется такое число
, найдется такое число  (
( ), что для всех
), что для всех  и удовлетворяющих условию
и удовлетворяющих условию  , выполняется неравенство
, выполняется неравенство  Обозначается
Обозначается  .
.
(по Гейне). Число  называется пределом функции
называется пределом функции  в точке
в точке  (или при
(или при  ), если для любой последовательности допустимых значений аргумента
), если для любой последовательности допустимых значений аргумента 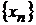 , сходящейся к
, сходящейся к  последовательность соответствующих значений функции
последовательность соответствующих значений функции  сходится к числу
сходится к числу  .
.
Пределы функции слева и справа называются односторонними пределами
Предел слева записывают так:  .
.
Аналогично определяется предел функции справа: 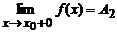 .
.
Для существования предела функции в точке необходимо и достаточно, чтобы
f (a - 0) = f(a + 0).
Функция f(x), заданная на всей числовой прямой, называется бесконечно большой при  , если для любого положительного числа
, если для любого положительного числа 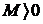 , найдется такое положительное число
, найдется такое положительное число 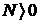 (зависящее от М, N=N(М)), что при всех х, удовлетворяющих условию
(зависящее от М, N=N(М)), что при всех х, удовлетворяющих условию  , выполняется неравенство.
, выполняется неравенство.
Число  называется пределом функции
называется пределом функции  при
при  , если для любого числа
, если для любого числа  , найдется такое число
, найдется такое число  (
( ), что для всех
), что для всех  , удовлетворяющих условию
, удовлетворяющих условию  , выполняется неравенство
, выполняется неравенство 
6. Бесконечно малые и бесконечно большие функции (определение бесконечно малой функции в точке и на бесконечности, свойства бесконечно малых функций).
Функция f(x) называется бесконечно малой при  , если
, если  .
.
Свойства бесконечно малых функций:
1)Сумма конечного числа бесконечно малых функций есть величина бесконечно малая;
2)Произведение конечного числа бесконечно малых функций, а также бесконечно малой функции на ограниченную функция, есть величина бесконечно малая;
3)Частное от деления бесконечно малой функции на функцию, предел которой не равен нолю, если величина бесконечно малая.
7. Сравнение бесконечно малых функций (три случая, таблица эквивалентных бесконечно малых функций).
Сравнение бесконечно малых функций:
1). Если  , то
, то  называется бесконечно малой, более высокого порядка малости, чем
называется бесконечно малой, более высокого порядка малости, чем  .
.
2). Если  , то
, то  и
и  называются бесконечно малыми одного порядка (имеют одинаковую скорость стремления к нолю);
называются бесконечно малыми одного порядка (имеют одинаковую скорость стремления к нолю);
3). Если  ,то
,то  и
и  называются эквивалентными бесконечно малыми, обозначаются
называются эквивалентными бесконечно малыми, обозначаются  ~
~  .
.
Эквивалентные бесконечно малые при  :
:
1. 
2. 
3. 
4. 
5. 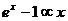
6. 
7. 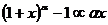
8. 
9. 
8. Основные теоремы о пределах (семь теорем).
Таблица основных интегралов
1.  . 11.
. 11.  .
.
2. 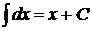 . 12.
. 12.  .
.
3.  . 13.
. 13.  .
.
4. 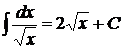 . 14.
. 14.  .
.
5.  . 15.
. 15.  .
.
6.  . 16.
. 16.  .
.
7.  . 17.
. 17. 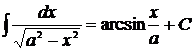 .
.
8.  . 18.
. 18.  .
.
9.  . 19.
. 19.  .
.
10.  . 20.
. 20.  .
.
25. Непосредственное интегрирование (основное понятие, часто встречающиеся преобразования дифференциала).
Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам называется непосредственным интегрированием.
Часто встречающиеся преобразования дифференциала:
1. Выражение не изменяется, если под знаком дифференциала к функции прибавить постоянную величину, т.е.
du=d(u+С), где С- число.
2. Если под знаком дифференциала функцию умножить на постоянную величину, все выражение нужно разделить на эту же постоянную величину, т.е.
 где С – число.
где С – число.
Формула  очень часто используется при вычислении интегралов. Например,
очень часто используется при вычислении интегралов. Например,

26. Метод подстановки в неопределенном интеграле (основное понятие, вывод формулы интегрирования).
Метод интегрирования подстановкой заключается во введение новой переменой интегрирования (т.е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся (в случае «удачной» подстановки). Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл 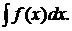 Сделаем подстановку
Сделаем подстановку  где
где  - функция, имеющая непрерывную производную.
- функция, имеющая непрерывную производную.
Тогда  и получаем формулу интегрирования подстановкой
и получаем формулу интегрирования подстановкой
 .
.
27. Интегрирование по частям в неопределенном интеграле (основное понятие, вывод формулы интегрирования).
Пусть u=u(x) и v=v(x) – функции, имеющие непрерывные производные. Тогда по правилу дифференцирования произведения имеем:  . Интегрируя это равенство, получим
. Интегрируя это равенство, получим  или
или

Полученная формула называется формулой интегрирования по частям. При ее применении подынтегральное выражение искомого интеграла разбивается на два сомножителя (u и dv). При переходе к правой части (2) первый из них дифференцируется ( ), второй интегрируется
), второй интегрируется  . Иногда эту формулу приходиться использовать несколько раз.
. Иногда эту формулу приходиться использовать несколько раз.
28. Правильные и неправильные рациональные дроби, выделение целой части у неправильной дроби (целая рациональная функция, дробно-рациональная функция, правильные и неправильные дроби, выделение целой части у неправильной дроби).
Целой рациональной функцией (многочленом) называется функция вида
 , (1)
, (1)
где а0, а1,…,аn – постоянные, называемые коэффициентами многочлена; число n – постоянная, называемая показателем степени многочлена.
Дробно-рациональной функцией (или рациональной дробью) называется функция, равная
отношению двух целых рациональных функций (многочленов), т.е.  , где Рm(х)- многочлен степени m, а Qn(x)- многочлен степени n.
, где Рm(х)- многочлен степени m, а Qn(x)- многочлен степени n.
Дробно-рациональная функция называется правильной, если степень числителя меньше степени знаменателя, т.е. m<n; в противном случае ( ) функция называется неправильной.
) функция называется неправильной.
Всякую неправильную дробно-рациональную функцию  можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(х) и правильной рациональной функции
можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(х) и правильной рациональной функции  , т.е.
, т.е.  .
.
29. Разложение правильной дроби на сумму простейших дробей, метод сравнивания коэффициентов (четыре основных вида простых дробей, три случая разложения правильных дробей на простейшие дроби, алгоритм метода сравнивания коэффициентов).
Простыми дробями называют дроби следующих типов:
1) 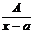 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ,
,
где A, M, N, a, p, q – действительные числа, k=2,3,…., m=2,3,….., квадратный трехчлен x2+px+q не имеет корней.
Рассмотрим 3 случая разложения дробно-рациональных функций:
1) Множители знаменателя линейные, они различны. Количество простых дробей равно показателю степени знаменателя.
 .
.
2) Наряду с линейными различными множителями знаменателя (которых может и не быть) присутствуют повторяющиеся линейные множители. Количество простых дробей равно показателю степени знаменателя.
 .
.
3) Наряду с линейными множителями знаменателя встречаются выражения второй степени, не разлагающиеся на линейные множители.
 .
.
Вопросы к экзамену
по дисциплине “Математический анализ”
Тема 1: Введение в анализ
1. Функциональная зависимость и виды её представления (основные понятия, способы задания функций, свойства функций).
— математическое понятие, отражающее связь между элементами множеств. записывается  или
или  .
.
Функция может быть задана тремя основными способами: аналитически, таблично или графически.
Функция  , определенная на множестве D называется четной, если для любых значений
, определенная на множестве D называется четной, если для любых значений 
 . Функции возрастающие, убывающие, неубывающие, невозрастающие называются монотонными функциями. Функции возрастающие, убывающие, называются строго монотонными функциями. Функция
. Функции возрастающие, убывающие, неубывающие, невозрастающие называются монотонными функциями. Функции возрастающие, убывающие, называются строго монотонными функциями. Функция  , определенная на множестве
, определенная на множестве  , называется периодической на этом множестве, если существует такое число
, называется периодической на этом множестве, если существует такое число 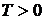 , что при любом
, что при любом  значение
значение 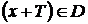 и
и 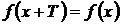 . При этом число
. При этом число 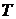 называется периодом функции.
называется периодом функции.
2. Классификация функций (простейшие элементарные функции, неявная, обратная и сложная функции, алгебраические и трансцендентные функции).
Функция называется явной, если она задана формулой, в которой правая часть не содержит зависимой переменной; например, функция у=х2 +5х + 1.Функция  аргумента
аргумента  называется неявной, если она задана уравнением
называется неявной, если она задана уравнением  , не разрешенным относительно зависимой переменной. Например, функция у(у>0), заданная уравнением х5 + у2 - х =0.
, не разрешенным относительно зависимой переменной. Например, функция у(у>0), заданная уравнением х5 + у2 - х =0.
Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными. К основным элементарным относятся следующие функции: степенная функция у=хα, α 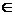 R; показательная функция у=ах, а › 0, а ≠1; логарифмическая функция y=logax, а › 0, а ≠1; тригонометрические формулы и обратные тригонометрические формулы. Алгебраической называется функция, в которой над аргументом проводится конечное число алгебраических действий.(целая рациональная функция, дробно-рациональная функция, иррациональная функция). Любая неалгебраическая функция называется трансцендентной. К числу трансцендентных функций относятся функции: показательная, логарифмическая, тригонометрические, обратные тригонометрические.
R; показательная функция у=ах, а › 0, а ≠1; логарифмическая функция y=logax, а › 0, а ≠1; тригонометрические формулы и обратные тригонометрические формулы. Алгебраической называется функция, в которой над аргументом проводится конечное число алгебраических действий.(целая рациональная функция, дробно-рациональная функция, иррациональная функция). Любая неалгебраическая функция называется трансцендентной. К числу трансцендентных функций относятся функции: показательная, логарифмическая, тригонометрические, обратные тригонометрические.
3. Преобразование графиков (все случаи с примером на графике).
Правило 1. Чтобы получить график функции  из графика функции
из графика функции  , нужно график функции
, нужно график функции  сдвинуть вдоль оси
сдвинуть вдоль оси 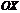 на
на  вправо, если
вправо, если  , или на
, или на  влево, если
влево, если 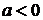 .
.
Правило 2. Чтобы получить график функции 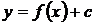 из графика функции
из графика функции  , нужно график функции
, нужно график функции  сдвинуть вдоль оси
сдвинуть вдоль оси  на
на  вверх, если
вверх, если  , или на
, или на  вниз, если
вниз, если  .
.
Правило 3. Чтобы получить график функции  из графика функции
из графика функции  , нужно график функции
, нужно график функции  зеркально отразить относительно оси
зеркально отразить относительно оси  .
.
Правило 4. Чтобы получить график функции  из графика функции
из графика функции  , нужно график функции
, нужно график функции  зеркально отразить относительно оси
зеркально отразить относительно оси 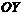 .
.
Правило 5. Чтобы построить график функции  , нужно значение ординаты графика функции
, нужно значение ординаты графика функции  умножить на число
умножить на число  , а абсциссу оставить без изменения.
, а абсциссу оставить без изменения.
Правило 6. Чтобы построить график функции  , нужно значение
, нужно значение  разделить на число
разделить на число  .
.
Правило 7. Чтобы получить график функции 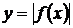 из графика функции
из графика функции  , надо участки графика функции
, надо участки графика функции  , лежащие выше оси
, лежащие выше оси  , оставить без изменения, а участки ниже оси
, оставить без изменения, а участки ниже оси 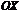 зеркально отразить относительно этой оси.
зеркально отразить относительно этой оси.
Правило 8. Чтобы получить график функции у= f(|х|) из графика функции  , надо построить график функции
, надо построить график функции  , при
, при  и отразить его зеркально относительно оси
и отразить его зеркально относительно оси 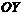 .
.
4. Предел числовой последовательности (понятие числовой последовательности, определение предела числовой последовательности, геометрический смысл предела числовой последовательности).
Числовая последовательность — это функция натурального аргумента: 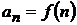 . Последовательность
. Последовательность 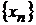 называется ограниченной сверху (снизу), если существует число
называется ограниченной сверху (снизу), если существует число  (число
(число  ) такое, что любой элемент
) такое, что любой элемент 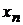 этой последовательности удовлетворяет неравенству
этой последовательности удовлетворяет неравенству  (
( ).
).
Число  называется пределом числовой последовательности
называется пределом числовой последовательности  , если для любого числа
, если для любого числа  , существует такой номер
, существует такой номер  , что для всех членов последовательности с номерами
, что для всех членов последовательности с номерами  выполняется неравенство
выполняется неравенство  .
.
Число a – предел последовательности xn, если в любую окрестность числа а, начиная с некоторого номера попадают все члены последовательности {xn}
5. Предел функции в точке (определение предела функции в точке, односторонние пределы, условие существования предела функции в точке, бесконечно большая последовательность определение предела функции на языке последовательностей, предел функции на бесконечности).
(по Коши). Число  называется пределом функции
называется пределом функции  при
при  , стремящимся к
, стремящимся к  (или в точке
(или в точке  ), если для любого, даже очень малого числа
), если для любого, даже очень малого числа  , найдется такое число
, найдется такое число  (
( ), что для всех
), что для всех  и удовлетворяющих условию
и удовлетворяющих условию  , выполняется неравенство
, выполняется неравенство  Обозначается
Обозначается  .
.
(по Гейне). Число  называется пределом функции
называется пределом функции  в точке
в точке  (или при
(или при  ), если для любой последовательности допустимых значений аргумента
), если для любой последовательности допустимых значений аргумента 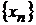 , сходящейся к
, сходящейся к  последовательность соответствующих значений функции
последовательность соответствующих значений функции  сходится к числу
сходится к числу  .
.
Пределы функции слева и справа называются односторонними пределами
Предел слева записывают так:  .
.
Аналогично определяется предел функции справа: 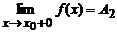 .
.
Для существования предела функции в точке необходимо и достаточно, чтобы
f (a - 0) = f(a + 0).
Функция f(x), заданная на всей числовой прямой, называется бесконечно большой при  , если для любого положительного числа
, если для любого положительного числа 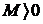 , найдется такое положительное число
, найдется такое положительное число 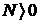 (зависящее от М, N=N(М)), что при всех х, удовлетворяющих условию
(зависящее от М, N=N(М)), что при всех х, удовлетворяющих условию  , выполняется неравенство.
, выполняется неравенство.
Число  называется пределом функции
называется пределом функции  при
при  , если для любого числа
, если для любого числа  , найдется такое число
, найдется такое число  (
( ), что для всех
), что для всех  , удовлетворяющих условию
, удовлетворяющих условию  , выполняется неравенство
, выполняется неравенство 
6. Бесконечно малые и бесконечно большие функции (определение бесконечно малой функции в точке и на бесконечности, свойства бесконечно малых функций).
Функция f(x) называется бесконечно малой при  , если
, если  .
.
Свойства бесконечно малых функций:
1)Сумма конечного числа бесконечно малых функций есть величина бесконечно малая;
2)Произведение конечного числа бесконечно малых функций, а также бесконечно малой функции на ограниченную функция, есть величина бесконечно малая;
3)Частное от деления бесконечно малой функции на функцию, предел которой не равен нолю, если величина бесконечно малая.
7. Сравнение бесконечно малых функций (три случая, таблица эквивалентных бесконечно малых функций).
Сравнение бесконечно малых функций:
1). Если  , то
, то  называется бесконечно малой, более высокого порядка малости, чем
называется бесконечно малой, более высокого порядка малости, чем  .
.
2). Если  , то
, то  и
и  называются бесконечно малыми одного порядка (имеют одинаковую скорость стремления к нолю);
называются бесконечно малыми одного порядка (имеют одинаковую скорость стремления к нолю);
3). Если  ,то
,то  и
и  называются эквивалентными бесконечно малыми, обозначаются
называются эквивалентными бесконечно малыми, обозначаются  ~
~  .
.
Эквивалентные бесконечно малые при  :
:
1. 
2. 
3. 
4. 
5. 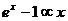
6. 
7. 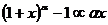
8. 
9. 
8. Основные теоремы о пределах (семь теорем).
Основные теоремы о пределах.
1) Функция не может иметь более одного предела.
2) Предел алгебраической суммы конечного числа функции равен сумме пределов этих функций, т.е.  /
/
3) Предел произведения конечного числа функции равен произведению пределов этих функций, т.е.  .
.
4)Предел частного двух функций равен частному пределов этих функций при условии, что предел знаменателя не равен нулю, т.е.  , где
, где  .
.
5) Если 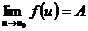 и
и  , то
, то  .
.
6)Если в некоторой окрестности точки 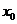 при достаточно больших
при достаточно больших 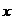 имеет место неравенство
имеет место неравенство  , то предел
, то предел 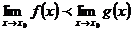 .
.
7) Если в некоторой окрестности точки 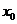 функция
функция  заключена между двумя функциями
заключена между двумя функциями  и
и  , т.е.
, т.е.  , то функция
, то функция  имеет тот же предел
имеет тот же предел  .
.
9. Первый и второй замечательные пределы.
Предел отношения 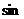 бесконечно малой дуги к самой дуге (выраженной в радианах) называется первым замечательным пределом и равен единице, т.е.
бесконечно малой дуги к самой дуге (выраженной в радианах) называется первым замечательным пределом и равен единице, т.е.  .
.
Предел последовательности с общим членом  при
при 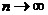 называется вторым замечательным пределом и равен числу
называется вторым замечательным пределом и равен числу  , т.е.
, т.е.  .
.
10. Непрерывность функции (определение непрерывности по Гейне и по Коши, классификация точек разрыва, кусочно-непрерывные функции).
Определение (по Гейне). Функция  называется непрерывной в точке
называется непрерывной в точке 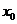 , если для любой последовательности значение аргумента
, если для любой последовательности значение аргумента  сходящейся к
сходящейся к 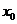 последовательность соответствующих значений функций, т.е.
последовательность соответствующих значений функций, т.е.  сходится к
сходится к 
|
|
|



 или
или  .
.
 . Функции возрастающие, убывающие, неубывающие, невозрастающие называются монотонными функциями. Функции возрастающие, убывающие, называются строго монотонными функциями. Функция
. Функции возрастающие, убывающие, неубывающие, невозрастающие называются монотонными функциями. Функции возрастающие, убывающие, называются строго монотонными функциями. Функция 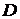 , называется периодической на этом множестве, если существует такое число
, называется периодической на этом множестве, если существует такое число 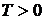 , что при любом
, что при любом  значение
значение 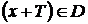 и
и 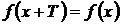 . При этом число
. При этом число 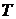 называется периодом функции.
называется периодом функции. аргумента
аргумента  называется неявной, если она задана уравнением
называется неявной, если она задана уравнением  , не разрешенным относительно зависимой переменной. Например, функция у(у>0), заданная уравнением х5 + у2 - х =0.
, не разрешенным относительно зависимой переменной. Например, функция у(у>0), заданная уравнением х5 + у2 - х =0.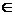 R; показательная функция у=ах, а › 0, а ≠1; логарифмическая функция y=logax, а › 0, а ≠1; тригонометрические формулы и обратные тригонометрические формулы. Алгебраической называется функция, в которой над аргументом проводится конечное число алгебраических действий.(целая рациональная функция, дробно-рациональная функция, иррациональная функция). Любая неалгебраическая функция называется трансцендентной. К числу трансцендентных функций относятся функции: показательная, логарифмическая, тригонометрические, обратные тригонометрические.
R; показательная функция у=ах, а › 0, а ≠1; логарифмическая функция y=logax, а › 0, а ≠1; тригонометрические формулы и обратные тригонометрические формулы. Алгебраической называется функция, в которой над аргументом проводится конечное число алгебраических действий.(целая рациональная функция, дробно-рациональная функция, иррациональная функция). Любая неалгебраическая функция называется трансцендентной. К числу трансцендентных функций относятся функции: показательная, логарифмическая, тригонометрические, обратные тригонометрические. из графика функции
из графика функции 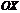 на
на  вправо, если
вправо, если  , или на
, или на  влево, если
влево, если 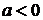 .
.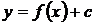 из графика функции
из графика функции  на
на  вверх, если
вверх, если  , или на
, или на  вниз, если
вниз, если  .
. из графика функции
из графика функции  .
. из графика функции
из графика функции 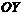 .
. , нужно значение ординаты графика функции
, нужно значение ординаты графика функции  , а абсциссу оставить без изменения.
, а абсциссу оставить без изменения. , нужно значение
, нужно значение 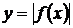 из графика функции
из графика функции  , оставить без изменения, а участки ниже оси
, оставить без изменения, а участки ниже оси 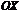 зеркально отразить относительно этой оси.
зеркально отразить относительно этой оси. и отразить его зеркально относительно оси
и отразить его зеркально относительно оси 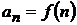 . Последовательность
. Последовательность 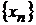 называется ограниченной сверху (снизу), если существует число
называется ограниченной сверху (снизу), если существует число  (число
(число  ) такое, что любой элемент
) такое, что любой элемент 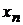 этой последовательности удовлетворяет неравенству
этой последовательности удовлетворяет неравенству  (
( ).
). называется пределом числовой последовательности
называется пределом числовой последовательности  , если для любого числа
, если для любого числа  , существует такой номер
, существует такой номер  , что для всех членов последовательности с номерами
, что для всех членов последовательности с номерами  выполняется неравенство
выполняется неравенство  .
. при
при  (или в точке
(или в точке  (
( ), что для всех
), что для всех  и удовлетворяющих условию
и удовлетворяющих условию  , выполняется неравенство
, выполняется неравенство  Обозначается
Обозначается  .
.  ), если для любой последовательности допустимых значений аргумента
), если для любой последовательности допустимых значений аргумента  сходится к числу
сходится к числу  .
.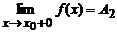 .
. , если для любого положительного числа
, если для любого положительного числа 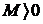 , найдется такое положительное число
, найдется такое положительное число 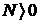 (зависящее от М, N=N(М)), что при всех х, удовлетворяющих условию
(зависящее от М, N=N(М)), что при всех х, удовлетворяющих условию  , выполняется неравенство.
, выполняется неравенство. , если для любого числа
, если для любого числа  (
( ), что для всех
), что для всех  , выполняется неравенство
, выполняется неравенство 
 , если
, если  .
. , то
, то  называется бесконечно малой, более высокого порядка малости, чем
называется бесконечно малой, более высокого порядка малости, чем  .
. , то
, то  ,то
,то  :
:



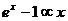

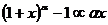


 . 11.
. 11.  .
.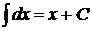 . 12.
. 12.  .
. . 13.
. 13.  .
.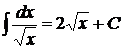 . 14.
. 14.  .
. . 15.
. 15.  .
. . 16.
. 16.  .
. . 17.
. 17. 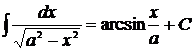 .
. . 18.
. 18.  .
. . 19.
. 19.  .
. . 20.
. 20.  .
. где С – число.
где С – число. очень часто используется при вычислении интегралов. Например,
очень часто используется при вычислении интегралов. Например,
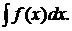 Сделаем подстановку
Сделаем подстановку  где
где  - функция, имеющая непрерывную производную.
- функция, имеющая непрерывную производную. и получаем формулу интегрирования подстановкой
и получаем формулу интегрирования подстановкой .
. . Интегрируя это равенство, получим
. Интегрируя это равенство, получим  или
или
 ), второй интегрируется
), второй интегрируется  . Иногда эту формулу приходиться использовать несколько раз.
. Иногда эту формулу приходиться использовать несколько раз. , (1)
, (1) , где Рm(х)- многочлен степени m, а Qn(x)- многочлен степени n.
, где Рm(х)- многочлен степени m, а Qn(x)- многочлен степени n. ) функция называется неправильной.
) функция называется неправильной. можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(х) и правильной рациональной функции
можно, путем деления числителя на знаменатель, представить в виде суммы многочлена L(х) и правильной рациональной функции  , т.е.
, т.е.  .
.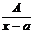 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4)  ,
, .
. .
. .
. /
/ .
. , где
, где  .
.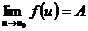 и
и  , то
, то  .
.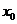 при достаточно больших
при достаточно больших 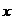 имеет место неравенство
имеет место неравенство  , то предел
, то предел 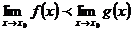 .
. заключена между двумя функциями
заключена между двумя функциями  , т.е.
, т.е.  , то функция
, то функция 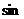 бесконечно малой дуги к самой дуге (выраженной в радианах) называется первым замечательным пределом и равен единице, т.е.
бесконечно малой дуги к самой дуге (выраженной в радианах) называется первым замечательным пределом и равен единице, т.е.  .
. при
при 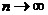 называется вторым замечательным пределом и равен числу
называется вторым замечательным пределом и равен числу  , т.е.
, т.е.  .
. называется непрерывной в точке
называется непрерывной в точке  сходящейся к
сходящейся к  сходится к
сходится к 

