МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПУТЕЙ СООБЩЕНИЯ (МИИТ)
Институт управления и информационных технологий
Кафедра «Вычислительные системы и сети»
Б.В. Желенков, В.Г. Першеев
ДИСКРЕТНАЯ МАТЕМАТИКА
Учебное пособие
Москва - 2008
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПУТЕЙ СООБЩЕНИЯ (МИИТ)
Институт управления и информационных технологий
Кафедра «Вычислительные системы и сети»
Б.В. Желенков, В.Г. Першеев
ДИСКРЕТНАЯ МАТЕМАТИКА
Рекомендовано редакционно-издательским советом
университета в качестве учебного пособия
для студентов I курса специальности «Вычислительные машины, комплексы, системы и сети» и направления
«Информатика и вычислительная техника»
по дисциплине
«Дискретная математика»
Москва - 2008
УДК 681.3
Ж 51
Желенков Б.В., Першеев В.Г. Дискретная математика: Учебное пособие.- М.: МИИТ, 2008. – 94 с.
В учебном пособии рассматриваются теория булевых функций, способы их аналитического представления и методы минимизации и теория построения комбинационных схем.
Рецензенты:
Профессор кафедры «Проектирование ВК» РГТУ им. Циолковского, к.т.н., В.В.Шилов
Профессор кафедры «Управление и информатика в технических системах» МИИТа, д.т.н. В.Г.Сидоренко
© Московский государственный университет путей сообщения (МИИТ), 2008
Св. план 2008г., поз.86
| Подписано к печати
Тираж 100 экз.
Усл.-печ. л. – 5,8
| Формат 60 х 84 1/16
Заказ –
|
127994, Москва, ул. Образцова, 15
Типография МИИТа
Содержание
| Введение.
|
|
| 1. Булевы функции (БФ).
|
|
| 1.1. Аналитическое представление БФ.
|
|
| 1.1.1. Дизъюнктивная совершенная нормальная форма.
|
|
| 1.1.2. Конъюнктивная совершенная нормальная форма.
|
|
| 1.2. Минимизация БФ.
|
|
| 1.2.1. Дизъюнктивная нормальная форма (ДНФ).
|
|
| 1.2.2. Пути решения задачи упрощения ДНФ БФ.
|
|
| 1.2.3. Построение СДНФ по ДСНФ.
|
|
| 1.2.4. Построение СДНФ по произвольной ДНФ.
|
|
| 1.2.5. Получение ТДНФ с помощью таблиц покрытий.
|
|
| 1.2.6. Недоопределенные БФ и способы их задания.
|
|
| 1.2.7. Построение простых импликант недоопределенных БФ методом проб.
|
|
| 1.2.8. Построение ТДНФ недоопределенных БФ.
|
|
| 1.2.9. Карты Карно.
|
|
| 2. Логические схемы (ЛС).
|
|
| 2.1.Основные понятия.
|
|
| 2.2. Использование скобочных преобразований ДНФ при синтезе КС из элементов типа И, ИЛИ, НЕ.
|
|
| 2.3. Синтез КС из элементов И-НЕ, ИЛИ-НЕ, И-ИЛИ-НЕ.
|
|
| 2.3.1. КС часто используемых БФ.
|
|
| 2.3.2. КС для произвольных БФ.
|
|
| 2.4. Разделительный метод синтеза схем минимальной глубины из элементов И-НЕ, ИЛИ-НЕ, И-ИЛИ-НЕ.
|
|
| 2.4.1. Базовая концепция.
|
|
| 2.4.2. Алгоритм разделения ТДНФ на К частей с минимизацией максимального веса.
|
|
| 2.4.3. Синтез КС из элементов И-НЕ.
|
|
| 2.4.4. Синтез КС из элементов ИЛИ-НЕ.
|
|
| 2.4.5. Синтез КС из элементов И-ИЛИ-НЕ.
|
|
| 2.4.6. Синтез КС из набора элементов.
|
|
| Литература
|
|
ВВЕДЕНИЕ
Основой теории цифровых устройств обработки информации является дискретная математика и, в частности, такие ее разделы как:
- теория графов;
- теория логических функций (в том числе булевых);
- теория логических схем и автоматов;
- теория алгоритмов;
- теория кодирования.
Изучение этого круга вопросов было начато в курсе «Основы информатики».
В рамках данного учебного пособия рассматриваются:
- теория булевых функций;
- теория комбинационных схем.
.
БУЛЕВЫ ФУНКЦИИ (БФ).
Пусть (X n-1,…X i,…X 1,X 0) – набор двоичных переменных (X i= 0;1). Множество всех наборов значений этих переменных обозначим Е n. Это 2 n наборов.
|
| Xn-1
| …
| Xi
| …
| X1
| X0
|
|
|
| …
|
| …
|
|
|
|
|
| …
|
| …
|
|
|
| 2n
|
| …
|
| …
|
|
|
|
| …
| …
| …
| …
| …
| …
|
|
|
| …
|
| …
|
|
|
|
|
|
|
|
|
|
|
Функция F(X n-1,…X i,…X 1,X 0) называется булевой, если она определена на Е n и принимает значения 0 или 1.
Множество наборов, на которых F = 1, обозначается М 1.
Множество наборов, на которых F = 0, обозначается М 0.
Известно, что формула булевой алгебры это формула, где в качестве операций над двоичными переменными используются инверсия, конъюнкция и дизъюнкция.
Известно, что булева формула задает БФ, которая всегда может быть представлена таблицей.
Вопросы теории БФ, которые мы будем рассматривать, таковы:
- как представить любую БФ в аналитическом виде;
- как преобразовывать аналитические представления с целью получения эквивалентных формул наименьшей сложности.
АНАЛИТИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ БФ.
МИНИМИЗАЦИЯ БФ.
Конъюнкция называется элементарной, если каждая переменная входит в нее только один раз.
Дизъюнкция элементарных конъюнкций называется дизъюнктивной нормальной формой (ДНФ).
Длиной ДНФ называется число конъюнкций, из которых она состоит.
ДНФ, имеющая наименьшую длину среди всех эквивалентных, называется кратчайшей.
Построение СДНФ по ДСНФ.
СДНФ строят, используя разные подходы, но при этом, можно выделить два основных:
1) Генерация всех возможных конъюнкций исходных переменных и проверка их на наличие свойств простой импликанты рассматриваемой БФ;
2) Формирование всех простых импликант БФ по конъюнкциям из исходной ДСНФ (либо некоторой ДНФ) БФ.
Первый подход порождает много разных методов, отличающихся по организации перебора вариантов при генерации кодов конъюнкций. Эти методы наиболее удобны и эффективны при «машинном» решении задач.
Проверки конъюнкций чаще всего выполняют по М0.
Рассмотрим пример.
Пусть F(X,Y,Z) имеет М 1= (001, 010,011,100,101,110) и, соответственно, М 0= (000,111).
Необходимо определить является ли конъюнкция  простой импликантой БФ F.
простой импликантой БФ F.
Для переменных (X,Y,Z) М 1 ( ) = (000, 001).
) = (000, 001).
Так как 000 - набор из М 0 (F), то М 1 ( )
)  М1(F).
М1(F).
Следовательно,  не является импликантой F, а тем более простой импликантой.
не является импликантой F, а тем более простой импликантой.
Второй подход проиллюстрируем с помощью метода построения СДНФ по ДСНФ, предложенного Квайном и усовершенствованного Мак - Класки.
Карты Карно.
Рассмотрим принципы визуальных методов минимизации БФ (карты Карно, диаграммы Вейча, графы и др.).
Множество всех наборов значений переменных представляется специальной фигурой.
Конъюнкция представляется наглядным графическим образом, легко обнаруживаемым на используемой специальной фигуре (правильная конфигурация.)
Поиск ДНФ - визуальный поиск покрытия области М 1 по правильными конфигурациями.
Поиск покрытия в основном за интуицией человека!
Рассмотрим функцию от двух переменных (n = 2).
Фигура, представляющая множество всех наборов значений переменных - плоскость.
 На плоскости - прямоугольная таблица, каждая клетка которой представляет набор значений переменных.
На плоскости - прямоугольная таблица, каждая клетка которой представляет набор значений переменных.
| X
Y
|
|
| Клетки размечаются
значениями функции

| X
| Y
| F
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В таблице выделяется прямоугольник из соседних клеток, число которых равно целой степени двух (правильная конфигурация) и функция в них принимает значение «1».
Код конъюнкции – набор значений переменных, описывающих клетки правильной конфигурации. Переменная, чье значение сохраняется неизменным во всех клетках конфигурации отображается в коде эти значением, остальные переменные - прочерком «-».
Конъюнкция получается по ее коду.
Рассмотрим пример.

Рассмотрим карту Карно для функции от трех переменных (n = 3).
Фигура, представляющая множество всех наборов значений переменных - развертка цилиндра (есть соседства через левый и правый край).

Примеры правильных конфигураций.

Примеры «неправильной» конфигурации.

Рассмотрим карту Карно для функции от четырех переменных (n = 4).
Фигура для всех наборов значений переменных - развертка тора (есть соседства через все края).
Поиск ДНФ сводится к поиску покрытий М1 по правильным конфигурациям.
Рассмотрим примеры.
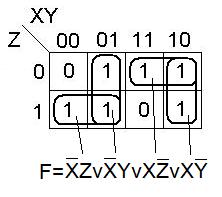
Данную функцию можно представить в более коротком виде.

Пример нахождения ДНФ для функции от 4-х переменных.

При построении ДНФ по карте Карно, критерием является ранг покрытия - число букв задаваемой им ДНФ. Наш задача – получить минимум.
Простая импликанта имеет образ правильной конфигурации, не являющейся частью одной другой.
Пример простой импликанты.

Для недоопределенной БФ F~ строится покрытие, у которого М 1  М ~
М ~  М
М  М 1
М 1
Все «единицы» должны быть покрыты и, при этом, могут быть покрыты клетки с «~», то есть клетки области неопределенности. Это позволяет уменьшить количество букв в ДНФ.
Рассмотрим пример.

Примечание.
Для нахождения МДНФ - области покрытия должны быть максимально возможными, а количество областей и их пересечение необходимо свести к минимуму.
Для нахождения СДНФ - области должны быть максимально возможными, должны быть представлены все возможные области (максимальное количество пересечений областей).
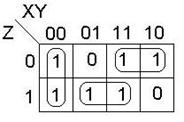
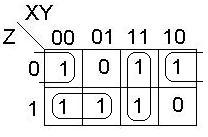
Рассмотрим пример нахождения СДНФ по карте Карно.

Рассмотрим пример нахождения МДНФ по карте Карно.

Карты (диаграммы) Вейча строятся аналогично картам Карно.
Правильная конфигурация здесь описывается конъюнкцией. По конъюнкции можно получить ее код, а затем по коду можно получить ее М 1.
(В картах Карно наоборот - по наборам получается код конъюнкции, а по коду сама конъюнкция.)

ЛОГИЧЕСКИЕ СХЕМЫ (ЛС).
ОСНОВНЫЕ ПОНЯТИЯ.
ЛС - это физические объекты, имеющие n входов и m выходов.


 n ЛС m
n ЛС m
На входы поступают сигналы, представляющие значения дискретных переменных. На выходах ЛС формируются сигналы - реакции на входные воздействия.
Чаще всего сегодня используются электрические сигналы, которые представляют двоичные переменные. «1» представляется высоким уровнем напряжения, например, +5 вольт, а «0» - низким уровнем, например, 0 вольт.
В ЛС закон, устанавливающий соответствие между реакцией и входным воздействием, можно описать БФ.
Это значит, что в любой момент времени набор значений двоичных переменных, представленный входными сигналами, однозначно определяет набор значений переменных, представленных выходными сигналами.
ЛС строятся из более мелких ЛС (неделимых в рамках рассмотрения), называемых логическими элементами (ЛЭ).
Процедура получения ЛС из ЛЭ заключается в том, что входы всех ЛЭ присоединяются либо к выходам других ЛЭ, либо к выходам источников входных сигналов.
Выходы некоторых лэ должны быть отмечены как выходы ЛС.
Все входы и выходы ЛЭ должны использоваться.
На вход любого ЛЭ не должен поступать сигнал, сформированный на выходе того же лэ. (Результат не должен зависеть сам от себя.) Иначе ЛС некорректна.
Рассмотрим пример некорректной ЛС.

Набор ЛЭ должен обладать свойством функциональной полноты - обеспечивать возможность построения из них ЛС, реализующих любые БФ.
К числу таких относятся ЛЭ, реализующие БФ:
- И, ИЛИ, НЕ - базовый теоретический набор;
- И - НЕ ( ) - элементы Шеффера;
) - элементы Шеффера;
- ИЛИ - НЕ ( ) - элементы Пирса;
) - элементы Пирса;
- и др.
Задача синтеза ЛС состоит в получении схемы из заданного набора ЛЭ. При этом можно говорить о схеме:
- с минимумом числа лэ;
- с минимумом числа последовательно соединенных лэ;
- с какими - то другими критериями качества;
- без использования критериев качества.
Простейший прием синтеза ЛС состоит в моделировании формулы, реализуемой БФ, схемой из заданных БФ.
Для этого нужно уметь строить схемы для БФ всех операций формулы.
Если БФ ЛЭ непосредственно реализуют операции, используемые в формуле, задача упрощается.
Рассмотрим пример.
Дано: F = 
Набор ЛЭ:

Построить ЛС, реализующую F из заданного набора ЛЭ.
Строим схему от выхода!

Если бы набор ЛЭ был другим, то для той же самой БФ, ЛС изменится.
Набор ЛЭ:

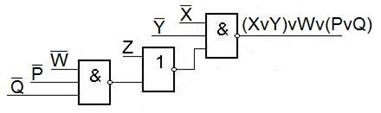
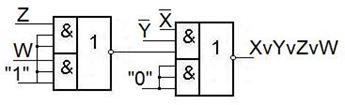
Формулу всегда можно представить ЛС, но есть ЛС не представимые формулой.
Это такие ЛС, в которых есть ЛЭ с выходами, идущими к нескольким ЛЭ.
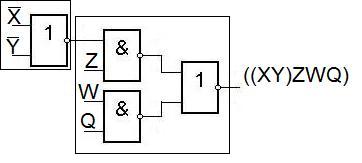
Пример.

Эту ЛС можно описать аналитически совокупностью БФ вида:
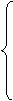
 F = F 1Ú F 2
F = F 1Ú F 2
F 1 = A& F 3 Такой прием пригоден
F 2 = D& F 3 для любой ЛС.
F 3 = B Ú C
Выполнив подстановки, мы получим
F = (A&(B Ú C)) Ú (D&(B Ú C)).
Построив по этой формуле ЛС, получим

Полученная ЛС не совпадает с исходной (сложнее).
Данный пример показывает, как получить аналитическое описание БФ в виде совокупности БФ для ЛС. Так (совокупностью БФ) можно описать любую ЛС.
Переходя от совокупности БФ к формуле, можно получить описание более сложной ЛС.
Формула не позволяет описывать ЛС, в которой объединены одинаковые части схемы.
Однако, имея формулу, можно получить по ней совокупность БФ, описывающую ЛС с объединенными одинаковыми частями схемы. (Этим объясняется наш интерес к формулам.)
В заключение отметим, что в настоящее время ЛС чаще всего называют комбинационные схемы, подчеркивая тем самым, что реакция схемы определяется комбинацией значений входных сигналов. Комбинационные схемы (КС) - термин, который мы будем использовать в дальнейшем.
ИСПОЛЬЗОВАНИЕ СКОБОЧНЫХ ПРЕОБРАЗОВАНИЙ ДНФ
СИНТЕЗ КС ИЗ ЭЛЕМЕНТОВ
И-НЕ, ИЛИ-НЕ, И-ИЛИ-НЕ.
КС часто используемых БФ.
Наиболее часто используемыми БФ являются конъюнкция, дизъюнкция, сумма «по модулю 2» и инверсия.
F = X1&X2& … &Xn
F = X1ÚX2Ú… ÚXn
F = X1 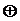 X2
X2 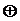 …
… 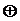 Xn
Xn
F = X1oX2o…oXn
где o - либо &, либо Ú, либо 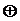 .
.
Существует набор стандартных решений для построения БФ.
Для этого используются следующие правила:
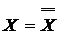
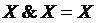
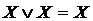
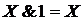
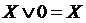
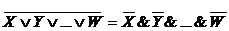
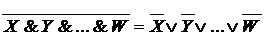
Для &, 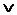 и
и 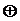 имеется свойство ассоциативности:
имеется свойство ассоциативности:
возможность произвольной расстановки скобок в формуле
F = X1oX2o…oXn
Например:
F = X1oX2o…oXn = X1o(X2(o…oXn))= (X1oX2)o(…oXn)
В зависимости от того, как расставляются скобки, можно получить выражение, задающее КС последовательной, пирамидальной или смешанной структуры.
Последовательная структура.
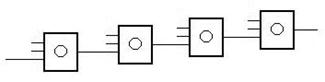
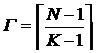 ;
; 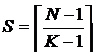
N - число переменных; К - число входов ЛЭ;
Г - глубина КС; S - число ЛЭ в КС.
Пирамидальная структура.
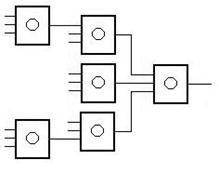
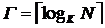 ,
, 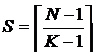
Смешанная структура.
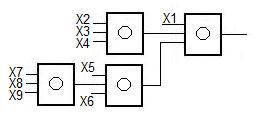
Мы увидели, как построить КС с n входами из ЛЭ (либо «блоков») с К входами, реализующими такие же функции, что и вся КС. Обратимся теперь к построению «блоков».
Рассмотрим типы используемых ЛЭ и их обозначения.
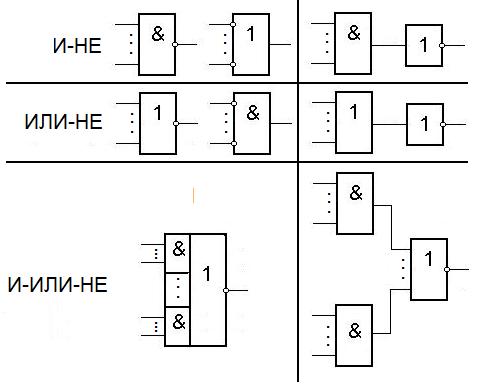
ЛЭ И - ИЛИ - НЕ таков, что из него путем подстановки констант или отождествления входов можно получать ЛЭ типа И - НЕ либо ИЛИ - НЕ.
Покажем это.
Рассмотрим способы получения инверторов из элементов И-НЕ, ИЛИ-НЕ, И-ИЛИ-НЕ.

Рассмотрим способы получения конъюнкции из элементов И-НЕ, ИЛИ-НЕ, И-ИЛИ-НЕ.
Получение конъюнкции из элементов И-НЕ.
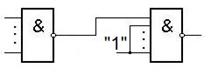
Получение конъюнкции из элементов ИЛИ-НЕ.
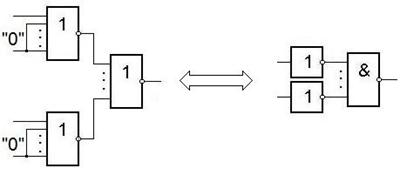
Получение конъюнкции из элементов И-НЕ и ИЛИ-НЕ.
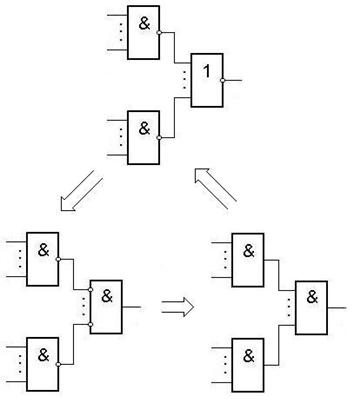
Получение конъюнкции из элементов И-ИЛИ-НЕ.
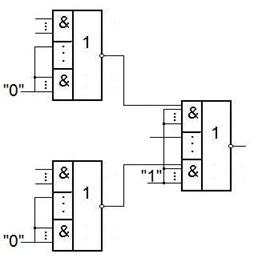
Рассмотрим примеры получения конъюнкций.
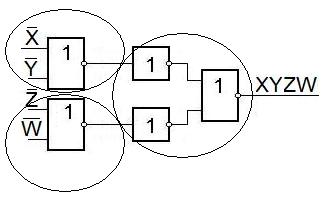
Получение дизъюнкции из элементов ИЛИ-НЕ.
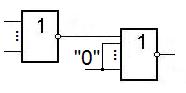
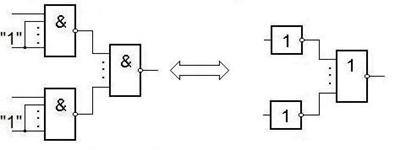
Получение дизъюнкции из элементов И-НЕ и ИЛИ-НЕ.
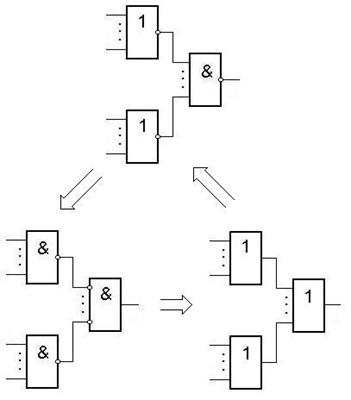
Получение дизъюнкции из элементов И-ИЛИ-НЕ.
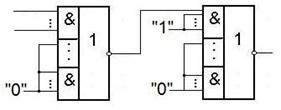
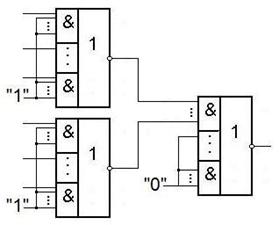
Рассмотрим примеры получения дизъюнкций.
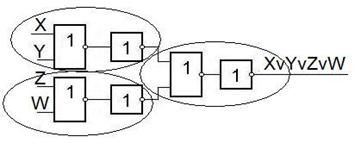
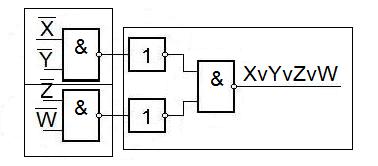
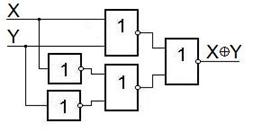
Теперь рассмотрим схемы для получения суммы по модулю два.
|
X
|
Y
| 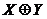
| 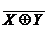
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
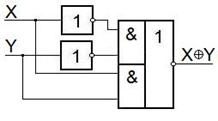
В соответствии с таблицей истинности можно получить несколько способов реализации этой функции.
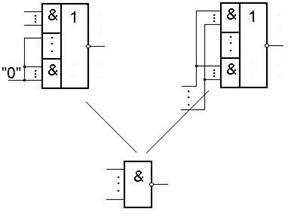
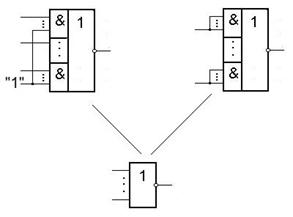
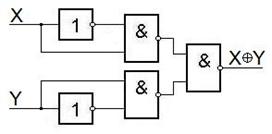
Первый способ – на элементах И-НЕ.
Второй способ – на элементах ИЛИ-НЕ.
Третий способ – на элементе И-ИЛИ-НЕ.
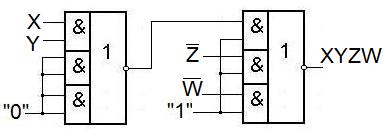
Рассмотрим использование выражений вида И - ИЛИ.
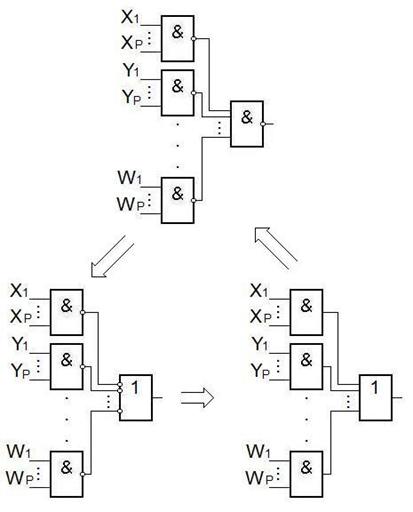
F=(X1&…&XP) 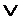 (Y1&…&YP)
(Y1&…&YP) 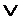 …
… 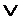 (W1&…&WP)
(W1&…&WP)
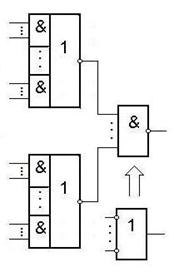
Рассмотрим примеры реализации выражений И-ИЛИ.
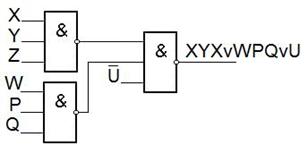
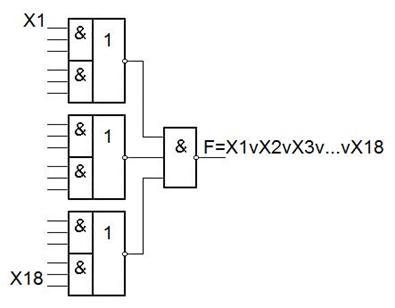
КС ДЛЯ ПРОИЗВОЛЬНЫХ БФ.
Процедура построения КС состоит из трех этапов:
1. Строится схема из элементов И, ИЛИ, НЕ.
2. Отдельные части схемы вида И - ИЛИ, либо И, либо ИЛИ переводятся в схемы из заданных ЛЭ (см. раздел 2.3.1).
3. Полученная КС корректируется с целью устранения возможной избыточности, например, вида
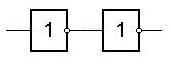
или нахождения общих частей.
Примечание.
Исходную схему (1 - ый этап) можно построить методами раздела 2.2 либо даже из других ЛЭ другими способами, а потом переводить на требуемые ЛЭ по частям.
Например, исходной может быть схема
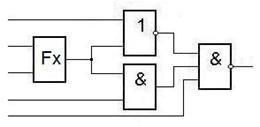
СХЕМ МИНИМАЛЬНОЙ ГЛУБИНЫ
ИЗ ЭЛЕМЕНТОВ
И-НЕ, ИЛИ-НЕ, И-ИЛИ-НЕ.
Базовая концепция.
Начинаем строить схему от выхода. Находим выходной ЛЭ и функции его входов для реализации бф F.

 j 1
j 1
 y F
y F

 j k
j k
F = y(j 1,j 2, ... j k).
Далее процедура повторяется для j 1,j 2, ... j k,пока для всех ЛЭ схемы в качестве функций входов будут получены независимые (отдельные) переменные или константы.
При этом в процессе построения схемы возникает две проблемы:
1. Выбрать «наилучший ЛЭ» из числа заданных;
2. Найти «наилучшую совокупность» функций входов ЛЭ.
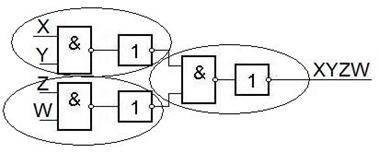
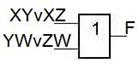
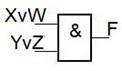
Рассмотрим пример возникновения первой проблемы.
| F = XYÚXZÚYWÚZW
|
| 
|
| XYÚXZÚYWÚZW = (XÚW)(YÚZ)
|
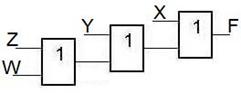
Рассмотрим пример возникновения второй проблемы.
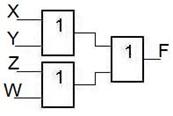
| F =XÚYÚZÚW
|
| 
|
| XÚ(Y(Ú(Z(ÚW)))
| (XÚY)Ú(ZÚW)
|
| Глубина схемы = 3
| Глубина схемы = 2
|
Нужно научится, для выбранного ЛЭ, сроить совокупность функций его входов и сравнивать результаты, полученные для разных ЛЭ.
Сравнение удобно выполнять с помощью оценок (весов) реализуемых БФ. Чем точнее оценка, тем сложнее она получается. Абсолютно точная оценка по сложности эквивалентна сложности полного перебора всех вариантов построения схем.
Простейшей оценкой может быть величина n, но такая оценка очень груба. Она не позволяет различать функции с одинаковым числом переменных.
F = XÚYÚZÚW; n = 4.
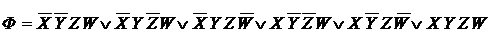 ; n = 4.
; n = 4.
Наилучшим образом учитывает индивидуальные свойства функций оценка БФ, получаемая по ТДНФ (вес W для ТДНФ).
Вычисление W для ТДНФ будет рассмотрено ниже.
Проведение предварительной оценки позволяет сравнивать варианты схем без их построения.
Если W(F 1) > W(F 2), то Г(F 1) > Г(F 2)
Г(F) - глубина КС, реализующей F.
Пусть имеем некоторую схему:

 j 1
j 1

 y F
y F
 j k
j k
и пусть оценки (веса) функций входов при этом:
W(j 1), W(j 2), …W(j K).
Таких схем может быть много. Для каждой из них получим веса.
Лучшей будет схема, в которой maxW(j J) для J от1 до k будет как можно меньше. (maxW определяет Г.)
Наша задача – нахождение иметь min(max(W(j J)) по разным вариантам выбора функций входов.
Любая приближенная оценка не может быть абсолютно точной, и из - за этого схема может быть не лучшей, но это плата за приемлемое время решения задачи.
Для получения функций входов ЛЭ будем пользоваться дизъюнктивными моделями ЛЭ (моделями из дизъюнкторов и инверторов).
Пример модели.
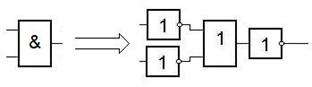
По такой модели, двигаясь от выхода ко входам, легко находить функцию входа инвертора (однозначно получается инверсией функции выхода) и функции входов дизъюнкторов (получаются разделением ТДНФ).
Рассмотрим пример реализации функции.
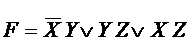
ТДНФ для F имеет вид 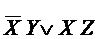 . Отсюда получим:
. Отсюда получим:
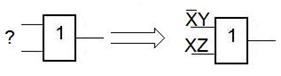
Замена исходной ДНФ на ТДНФ, в данном примере дала упрощение функций входов и, соответственно, даст упрощение схемы их реализующей.
Но дело не только в этом.
Если разделение делать не по ТДНФ, то процедура синтеза может не сходиться (будем строить схему до бесконечности).
Для реализации БФ F в процессе синтеза может потребоваться реализация БФ F. ?!
Рассмотрим пример.
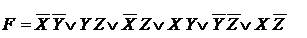
Построим карту Карно для данной функции.
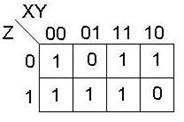
Выполним поиск ТДНФ
В итоге получаем две ТДНФ.
Если начать разделение F по исходному выражению, то можно получить схему вида
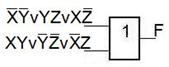
Что соответствует 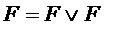
Вес W для F рассчитывается по ТДНФ этой функции.
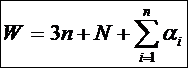
где N - число букв ТДНФ;
a i= 0, если i - ая переменная входит в ТДНФ либо только в прямом, либо только в инверсном виде, иначе a i= 1.
Рассмотрим пример.
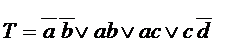
W = 3 * 4 + 8 + (1 + 1 + 0 + 0) = 22.
Другой способ подсчета веса ТДНФ выполняется следующим образом:
Первое появление переменной вносит в вес значение – 4.
Первое появление инверсии бывшей ранее буквы – 2.
Повторное появление буквы – 1.
При выполнении суммирования этих весов получим ту же величину W. Порядок просмотра может быть любым.
Рассмотрим пример.
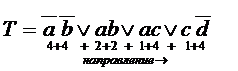
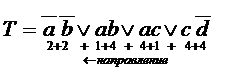
В обоих случаях W = 22.
Умея подсчитывать W, можно научиться разделять ТДНФ на части так, чтобы maxW среди весов отдельных частей был по возможности минимальным. Решив эту задачу, можно научиться строить схемы минимальной глубины по дизъюнктивным моделям ЛЭ.
Примечание.
Одинаковые части, получающиеся в КС, следует объединять. (В процессе построения КС или после завершения работ по п.8.)
Рассмотрим пример реализации БФ на элементах 2И-3ИЛИ-НЕ.

1 и 2 Находим по карте Карно инверсию функции и ТДНФ 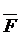

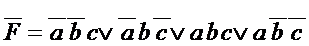

3. Делим полученную ТДНФ на три части.

4;5. 
6. Делим каждую из частей на две.
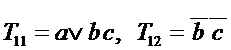
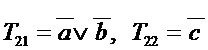 ,
, 
Если получились отдельные переменные, то мы их инвертируем и получаем функции входов, а другие Тij продолжим обрабатывать по сокращенному алгоритму.

3. Делим ТДНФ на три части.




4;5. 



6. Делим каждую из частей на две.



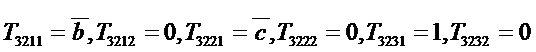
Все функции содержат по одной переменной или константе, следовательно будем получать функции входов и строить схему.
7. Инвертируем Т для получения функций входа.



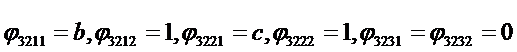
Теперь построим схему.

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ПУТЕЙ СООБЩЕНИЯ (МИИТ)
Институт управления и информационных технологий



 простой импликантой БФ F.
простой импликантой БФ F. ) = (000, 001).
) = (000, 001). )
)  М1(F).
М1(F). не является импликантой F, а тем более простой импликантой.
не является импликантой F, а тем более простой импликантой. На плоскости - прямоугольная таблица, каждая клетка которой представляет набор значений переменных.
На плоскости - прямоугольная таблица, каждая клетка которой представляет набор значений переменных.












 М ~
М ~  М
М 











 n ЛС m
n ЛС m
 ) - элементы Шеффера;
) - элементы Шеффера; ) - элементы Пирса;
) - элементы Пирса;




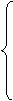
 F = F 1Ú F 2
F = F 1Ú F 2 
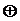 X2
X2 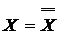
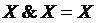
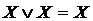
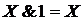
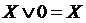
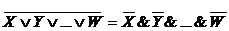
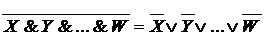
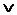 и
и 
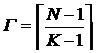 ;
; 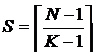

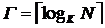 ,
, 



















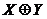
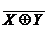
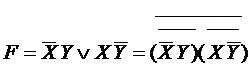
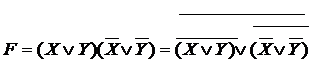
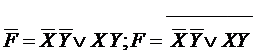

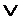 (Y1&…&YP)
(Y1&…&YP) 





 j 1
j 1 y F
y F
 j k
j k



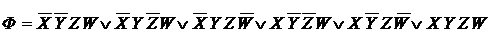 ; n = 4.
; n = 4.

 y F
y F
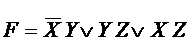
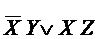 . Отсюда получим:
. Отсюда получим:
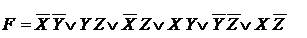

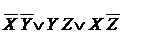
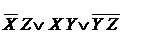

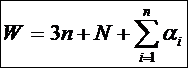
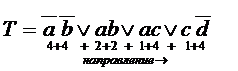
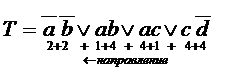





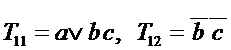
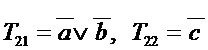 ,
,