Геометрический смысл определённого интеграла
Из истории математики известно, что одной из первых задач, приведшей к понятию определенного интеграла, является задача о вычислении площади криволинейной трапеции.
Определение:
Простейшей криволинейной трапецией будем называть фигуру, ограниченную
сверху – кривой y=f (x)
снизу – осью абсцисс y=0
слева – прямой x=a
справа – прямой x=b (см. рис. 1)

Рис. 1
1. Весь отрезок [ a, b ] разобьем на п частичных промежутков [ xi, хi+1 ] длиной ∆xi = xi – хi-1 , (i=1, 2, …, n), х0 = a, xп = b.
2. В каждом частичном промежутке произвольно выберем точку

3. Составим интегральную сумму

Очевидно, геометрически эта формула выражает площадь ступенчатой фигуры, составленной из прямоугольников (см. ниже рис. 2)

Рис. 2
4. Перейдем к пределу при п → ∞ при условии, что 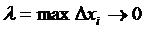
 (3)
(3)
При достаточно общих предположениях площадь ступенчатой фигуры стремится к площади криволинейной трапеции
Определение
Если существует конечный предел (3), то он называется определённым интегралом от функции f (х) по промежутку [ a, b ] и обозначается

Числа а и b называются, соответственно, нижним и верхним пределами интегрирования, а функция f (x) – интегрируемой.
Отметим, что построенный по схеме 1) – 4) интеграл называется интегралом Римана. Однако, при менее жестких ограничениях на подинтегральную функцию такой интеграл может не существовать. Тем не менее, потребности прежде всего современной физики привели к созданию интеграла Лебега, обслуживающего более широкий класс функций. В математике используются и другие конструкции интеграла
Механический смысл определённого интеграла
Если известна скорость v (t) некоторого объекта в зависимости от времени t, то с помощью интегрирования можно легко определить пройденный этим объектом путь s (t), а именно,

По аналогии, если известно ускорение a (t) некоторого объекта в зависимости от времени t, то с помощью интегрирования можно легко определить скорость движения этого объекта, а именно,

Предположим, что тело движется равноускоренно с ускорением а на временном периоде (0, t), причем в начальный момент времени скорость и путь равны нулю, т.е. a (t)= v ’(t)= a, v (0)= 0, s (0)= 0. Тогда


Итак, справедливы известные из школьного курса физики формулы


Ниже на графике ускорения (рис. 3) скорость тела численно равна площади заштрихованного прямоугольника

Рис. 3
Ниже на графике скорости (рис. 4) путь, пройденный телом за время (0, t), численно равен площади заштрихованного треугольника
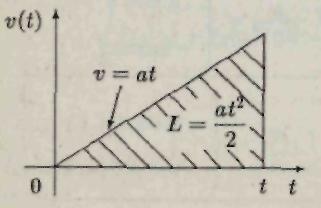
Рис. 4
Теорема Ньютона-Лейбница
Пусть функция f (х) определена, непрерывна и интегрируема на отрезке [ a, b ].
Определение
Интегралом с переменным верхним пределом называется интеграл следующего вида:

Здесь х – переменный верхний предел (a<x<b), t – переменная интегрирования (a<t<x). Геометрически интеграл с переменным верхним пределом означает площадь простейшей криволинейной трапеции, ограниченной справа прямой t=x. (см. рис. 5)

Рис. 5
Имеет место утверждение
Производная от интеграла с переменным верхним пределом равна подинтегральной функции
 (4)
(4)
Доказательство. Рассмотрим приращение  функции F (x) в точке х:
функции F (x) в точке х:

По определению имеем
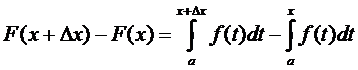 (5)
(5)
Из рисунка 5 видно, что правую часть равенства (5) можно интерпретировать так: из трапеции aAD (x+  )вычитается трапеция aACx. Ясно, что после вычитания остается узкая криволинейная трапеция xCD (x+
)вычитается трапеция aACx. Ясно, что после вычитания остается узкая криволинейная трапеция xCD (x+  ) с основанием
) с основанием  . Ее площадь выражается интегралом
. Ее площадь выражается интегралом
 (6)
(6)
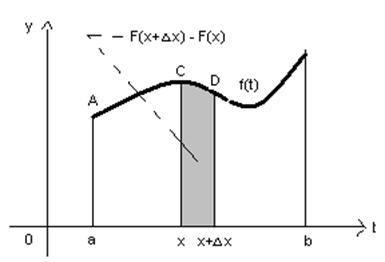
Рис. 6
По предположению функция y=f (x) непрерывна на промежутке [ a, b ]. Это позволяет считать, что площадь узкой криволинейной трапеции (на рис. 6 – закрашенная область) приблизительно равна площади прямоугольника с таким же основанием  и высотой f (с), где
и высотой f (с), где  . (см. рис. 7)
. (см. рис. 7)

Рис. 6
Таким образом, равенство (6) можно заменить приближенным равенством

или

Переходя к пределу при  , получаем
, получаем

что и требовалось доказать
Формула Ньютона-Лейбница
Пусть функция f (х) определена, непрерывна и интегрируема на отрезке [ a, b ]. Тогда определённый интеграл находится по формуле:

Действительно,

{согласно теореме Лагранжа о дифференцируемой функции}
= 
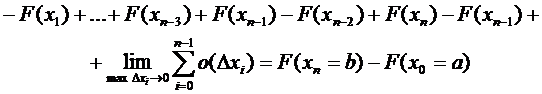
В определённом интеграле
Рассмотрим два простейших приема определенного интегрирования. Пусть функция f (x) имеет первообразную F (x). Покажем, что интеграл с переменным верхним пределом  также является первообразной функцией относительно f (x).
также является первообразной функцией относительно f (x).
Вычислим производную от интеграла с переменным верхним пределом:
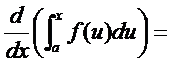
{воспользуемся формулой Ньютона-Лейбница}
= 
Далее  - первообразная f (x)
- первообразная f (x)
Верно ли тождество
 ?
?
Да, верно. В самом деле, переобозначение переменной интегрирования — это не замена переменной интегрирования.
Не всякий определённый интеграл с переменным верхним пределом может быть выражен в виде комбинации элементарных функций. В качестве примера таких интегралов, которые получили название специальных функций, приведём
 — интегральный синус
— интегральный синус
 — интеграл вероятностей
— интеграл вероятностей
Теорема о среднем
Пусть функция f (x) непрерывна на отрезке [ a, b ]. Тогда найдется такая точка ξ  (a, b), что выполняется равенство
(a, b), что выполняется равенство
 , где ξ
, где ξ  (a, b)
(a, b)
Для обоснования этого равенства будем исходить из формулы Ньютона-Лейбница

{по теореме Лагранжа} =
= 
Каков геометрический смысл теоремы о среднем?
Всегда можно подобрать такую высоту прямоугольника, чтобы его площадь равнялась площади криволинейной трапеции с тем же основанием.
Оценка интеграла
m (b – a) <  < М (b – a), где
< М (b – a), где 
Это двойное неравенство является очевидным следствием теоремы о среднем
Пусть f [ u (x)] непрерывна, а функция u (х) дифференцируема на [ а, b ], причём u (а) = с, u (b) = d. Тогда

Заметим, что пределы интегрирования изменяются. Итак, формула замены переменной в определенном интеграле такова:

Пример 1. Вычислить  .
.
Решение.

Выполним перенос производной под знаком интеграла  , если функции u (х) и v (x) дифференцируемы на отрезке [ a, b ]. Для этого используем формулу дифференцирования произведения функций
, если функции u (х) и v (x) дифференцируемы на отрезке [ a, b ]. Для этого используем формулу дифференцирования произведения функций
 или
или 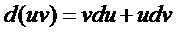
Теперь проинтегрируем это равенство

и окончательно получим:

Итак, формула интегрирования по частям в сокращенной записи такова:

Пример 2. Вычислить интеграл  .
.
Решение.

Решение.

Найдем объём тела вращения, если он ограничен плоскостями х = а, х = b и поверхностью, образованной вращением кривой у = f (x).
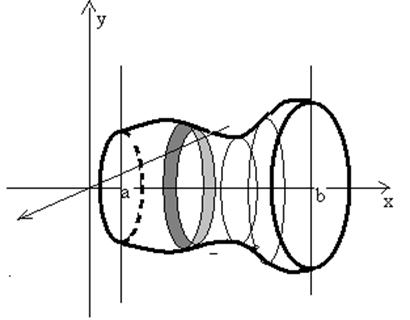
В качестве элемента интегральной суммы примем объём диска:


Переходя к пределу при  , получаем следующую формулу вычисления объема тела вращения:
, получаем следующую формулу вычисления объема тела вращения:

Пример 2. Найти объем шара радиуса R.
Решение. Вращением какой кривой описывается шар? Ответ: Вращением полуокружности. Уравнение верхней центральной полуокружности радиуса R:  Отсюда получаем
Отсюда получаем
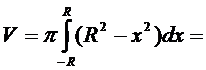

Несобственные интегралы
До сих пор мы занимались вычислением интегралов на ограниченном промежутке от ограниченной функции. В некоторых случаях эти ограничения на область и на функцию можно снять.Однако, прежде чем вычислять, такие интегралы необходимо сначала исследовать на сходимость.
Интеграл называется несобственным интегралом 1 рода, если его область интегрирования неограниченна, т.е. один из пределов или оба сразу принимают бесконечные значения
Интеграл называется несобственным интегралом 2 рода, если его подынтегральная функция неограниченна, т.е. минимум или (и) максимум функции в некоторой точке промежутка интегрирования принимают бесконечные значения
Говорят, что несобственный интеграл сходится, если существует предел этого интеграла в точке разрыва подынтегральной функции или в бесконечно удалённой точке. В противном случае говорят, что несобственный интеграл расходится
Решение.
 .
.
Ответ: Заданный интеграл расходится
Формула прямоугольников
Формула трапеций
Геометрический смысл определённого интеграла
Из истории математики известно, что одной из первых задач, приведшей к понятию определенного интеграла, является задача о вычислении площади криволинейной трапеции.
Определение:
Простейшей криволинейной трапецией будем называть фигуру, ограниченную
сверху – кривой y=f (x)
снизу – осью абсцисс y=0
слева – прямой x=a
справа – прямой x=b (см. рис. 1)

Рис. 1
1. Весь отрезок [ a, b ] разобьем на п частичных промежутков [ xi, хi+1 ] длиной ∆xi = xi – хi-1 , (i=1, 2, …, n), х0 = a, xп = b.
2. В каждом частичном промежутке произвольно выберем точку

3. Составим интегральную сумму

Очевидно, геометрически эта формула выражает площадь ступенчатой фигуры, составленной из прямоугольников (см. ниже рис. 2)

Рис. 2
4. Перейдем к пределу при п → ∞ при условии, что 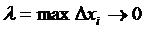
 (3)
(3)
При достаточно общих предположениях площадь ступенчатой фигуры стремится к площади криволинейной трапеции
Определение
Если существует конечный предел (3), то он называется определённым интегралом от функции f (х) по промежутку [ a, b ] и обозначается

Числа а и b называются, соответственно, нижним и верхним пределами интегрирования, а функция f (x) – интегрируемой.
Отметим, что построенный по схеме 1) – 4) интеграл называется интегралом Римана. Однако, при менее жестких ограничениях на подинтегральную функцию такой интеграл может не существовать. Тем не менее, потребности прежде всего современной физики привели к созданию интеграла Лебега, обслуживающего более широкий класс функций. В математике используются и другие конструкции интеграла







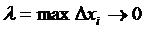
 (3)
(3)










 (4)
(4) функции F (x) в точке х:
функции F (x) в точке х:
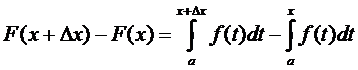 (5)
(5) )вычитается трапеция aACx. Ясно, что после вычитания остается узкая криволинейная трапеция xCD (x+
)вычитается трапеция aACx. Ясно, что после вычитания остается узкая криволинейная трапеция xCD (x+  (6)
(6)
 . (см. рис. 7)
. (см. рис. 7)


 , получаем
, получаем



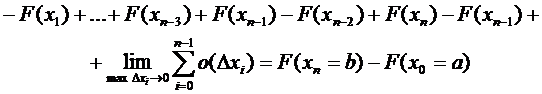
 также является первообразной функцией относительно f (x).
также является первообразной функцией относительно f (x).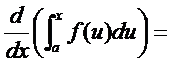

 - первообразная f (x)
- первообразная f (x) ?
? — интегральный синус
— интегральный синус — интеграл вероятностей
— интеграл вероятностей (a, b), что выполняется равенство
(a, b), что выполняется равенство , где ξ
, где ξ 

 < М (b – a), где
< М (b – a), где 


 .
.
 , если функции u (х) и v (x) дифференцируемы на отрезке [ a, b ]. Для этого используем формулу дифференцирования произведения функций
, если функции u (х) и v (x) дифференцируемы на отрезке [ a, b ]. Для этого используем формулу дифференцирования произведения функций или
или 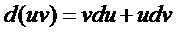



 .
.




 , получаем следующую формулу вычисления объема тела вращения:
, получаем следующую формулу вычисления объема тела вращения:
 Отсюда получаем
Отсюда получаем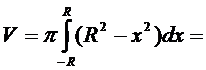

 .
.


