Отображения, осуществляемые элементарными функциями

Функция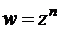

Положим 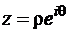. Тогда 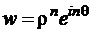, то есть аргумент образа точки z изменяется в n раз, модули образа и прообраза связаны степенной зависимостью. Тем самым для 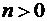образом сектора круга радиуса R с углом раствора 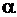и с центром в начале координат плоскости z (рис. 1.6, а) будет на плоскости w сектор круга радиуса 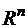с углом раствора 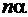и с центром в точке 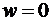(рис. 1.6, б).

В частности, если на плоскости z взять сектор с углом 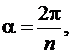то его образом будет полный круг плоскости w с разрезом вдоль положительной части действительного диаметра (рис. 1.6, в). Если же при 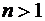угол 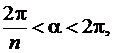то сектор на плоскости w будет иметь угол раствора больший, чем 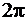, т.е. образы некоторых различных точек z будут иметь одинаковые декартовы координаты (но при различных значениях аргумента, различающихся на 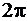, 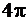и т.д. см. выделенный сектор на рис. 1.6, г). Такие поверхности называются неоднолистными римановыми поверхностями.

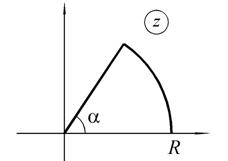
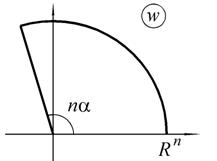
а б

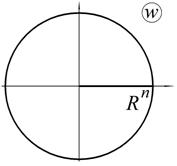
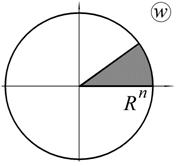
в г

Рис. 1.6. Отображение сектора круга функцией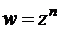

 

По определению степенной функции при отображении приращение аргумента образа изменяется в n раз, каково бы ни было его значение, т.е. функция 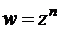определена, вообще говоря, на бесконечнолистной поверхности 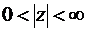, 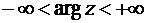. Однако, для рациональных 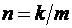(k, m – целые числа, не имеющие общих множителей) декартовы координаты образов точек 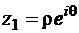и 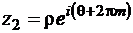, аргумент которых отличается на 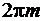, совпадают. Рассмотрим сектор плоскости z с углом раствора 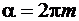. Луч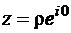и и 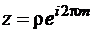являющиеся границами сектора на плоскости z, а также их образы 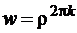и 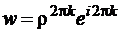совпадают. Тем самым, функци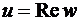и и 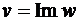изменяются непрерывно при переходе через эти лучи и, в связи с этим, являются дифференцируемыми. Поэтому можно считать, что берега разрезов «склеиваются» т. е. функция 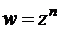при 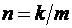аналитична на m -листной поверхности z, а ее образ представляет собой k -листную поверхность w. При этом , 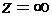; – особые точки функции (с нулевой либо бесконечной производной 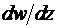), в которых нарушаются свойства конформности отображения (в частности, не сохраняются углы).

Для 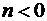точка 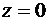переходит в 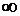, остальные свойства сохраняются. Поэтому образом сектора круга z будет на плоскости w внешняя часть сектора круга, ограниченная дугой окружности 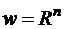и лучам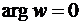и и 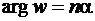(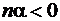, см. рис. 1.7). В частности, функция 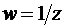отображает внутренность единичного круга на внешность и наоборот.

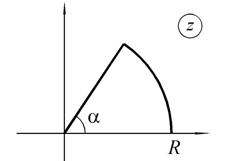
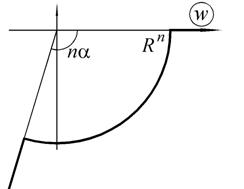
Рис. 1.7. Отображение сектора круга функцией 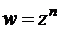при n <0

Функция Жуковского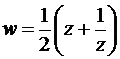

В этом случае точка является особой, ее образом является бесконечно удаленная точка плоскости w. Рассмотрим верхнюю часть круга единичного радиуса (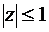, , 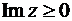рис. 1.8, а)). Образами радиусов OA и OB (рис. 1.8) являются участки действительной прямо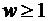й Re и Re 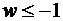соответственно. Образом полуокруж­ности , 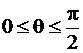– является отрезок 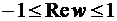(поскольку 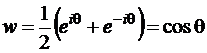). Тем самым, учитывая направление обхода границы, заключаем, что образом всего полукруга является нижняя полуплоскость .

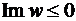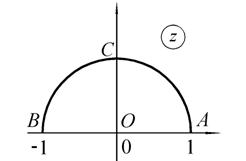
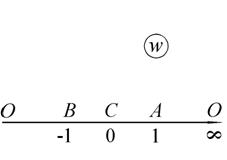
а б

Рис. 1.8. Отображение полукруга с помощью функции Жуковского

 

Аналогично рассуждая, получим, что образом нижнего полукруга будет верхняя полуплоскость. Таким образом, образом всего единичного круга является плоскость с разрезом по отрезку прямой 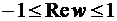. Поскольку подстановка в выражение функции Жуковского обратной величины 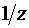вместо z не приводит к каким либо изменениям, то образом внешности круга будет та же плоскость с разрезом, а образом всей плоскости z – двулистная поверхность, состоящая из двух плоскостей с указанными выше разрезами, «склеенными крест-накрест».

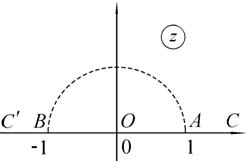
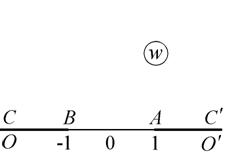
Теперь найдем образ верхней полуплоскости (рис. 1.9, а), возникающий при применении функции Жуковского. Как было сказано выше, образом полуокружности является отрезок 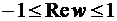, а образом верхнего полукруга – нижняя полуплоскость. Образом дополнения полукруга до полуплоскости является верхняя полуплоскость. Таким образом, образом всей верхней полуплоскости является плоскость с разрезами, проведенными от точек -1 и 1 на бесконечность (рис. 1.9, б).

а б

Рис. 1.9. Отображение полуплоскости с помощью функции Жуковского

 

Функция Жуковского часто используется для приложений в гидроаэродинамике, поскольку разные окружности плоскости z отображаются на разрез в виде дуги окружности, эллипс, или на кривую, изображающую профиль крыла самолета (профили Жуковского).

 

Функция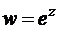

Поскольку 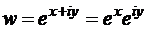, то y играет роль аргумента точек образа на плоскости w, а 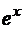– модуля. Если на плоскости z вырезать прямоугольник 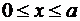, , 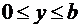на плоскости w горизонтальным участкам будут соответствовать линии постоянного аргумента (участки лучей, проведенных из начала координат), а вертикальным – линии постоянного модуля (радиуса), т. е. дуги окружностей. Образом всего прямоугольника является сектор кольца (рис. 1.10).

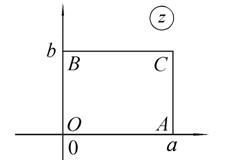
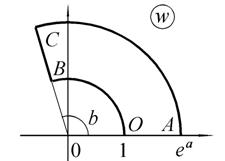
Рис. 1.10. Отображение с помощью функции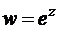

Рассмотрим частный случай отображения полуполосы (рис. 1.11, а) на верхний полукруг (рис. 1.11, б). Функция 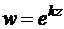отображает полуполосу на сектор единичного круга с углом kb. Поэтому выберем 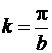. Функция 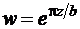осуществляет искомое отображение.

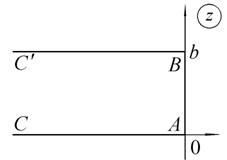
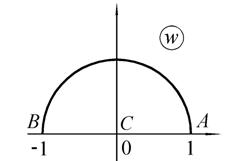
а б

Рис. 1.11. Отображение полуполосы с помощью функции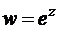

Если рассмотреть симметричную относительно AB полуполосу, то образом, полученным при применении функции 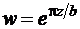будет дополнение единичного полукруга до полуплоскости. Тем самым, образом полосы 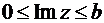является верхняя полуплоскость w.

 

Функция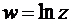

Эта функция является обратной к рассмотренной выше экспоненциальной зависимости.

Представим z в полярных координатах: 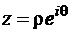. Тогда 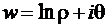. Исходя из этого, можно заключить, что с ее помощью кольцевой сектор (r₁£r£r₂ q₁£q£q₂) плоскости z отображается на прямоугольник (lnr₁£Re w £lnr₂, q₁£Im w £q₂) плоскости w. Однако при этом необходимо знать аргумент точки z (а не только ее декартовы координаты), поскольку изменение аргумента на 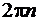, которое не меняет положение точки на плоскости z, приводит к изменению положения образа на .

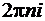Отметим, что если r₁=0, а r₂=¥, (т.е. область представляет собой внутренность угла), то образом такой области на плоскости w является горизонтальная полоса q₁<Im w <q₂.

 

Дробно-линейное отображение

Функция, осуществляющая данное отображение, имеет вид 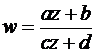, где a, b, c, d – комплексные постоянные (поскольку рассматриваются функции, отличные от константы, то дробь должна быть несократимой, т.е. ).

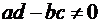Отметим, что , .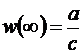

 

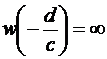Теорема 9. Если функция 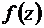всюду однолистна и аналитична в полной плоскости z, кроме точки C, то она дробно-линейна.