

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...
Топ:
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж...
Интересное:
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Содержание
Задача 1. Для заданных множеств А, В и С найдите: 2
Задача 2. Даны отображения (числовые функции) ƒ и g.. 5
Задача 3. Используя таблицу истинности и аналитические преобразования, установить эквивалентность функций в формулах.. 8
Задача 4.Определить к каким классам относится функция…… 9
Задача 5. Необходимо для данной функции найти её СДНФ, СКНФ, ЭСНФ, ИСНФ: 10
Задача 6. Используя метод Квайна, необходимо найти МДНФ функции, принимающей значения 1 на наборах.. 11
Задача 7. Используя метод Квайна – Мак-Класки, необходимо найти МДНФ функции, принимающей. 13
Задача 8. Используя метод диаграмм Вейча, необходимо найти МДНФ функции, принимающей значение 1 15
Задача 9. Задать граф. 17
Задача 10. Определить следующие основные характеристики графа: 18
Задача 11. Определить, является ли данный граф: 19
Задача 12. Определить метрические характеристики графа. 21
Список литературы.. 23
Задача 1. Для заданных множеств А, В и С найдите:
А È В, А È С, В È С, А È В È С, А Ç В, А Ç С, В Ç С, А Ç В Ç С, A \ B, B \ A, A \ C, C \ A, B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А Å B, А Å С, B Å C, A Å B Å C. Изобразите на плоскости А ´ В, А ´ С, В ´ С. Найдите 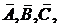 считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).
считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).
А = [-3; 0] – отрезок числовой оси
В = (-1; 3] – полуинтервал на числовой оси
С = (-0.5; 4) – интервал на числовой оси
Решение:
Объединением двух множеств A и B называется множество, состоящее из всех элементов, являющихся элементами хотя бы одного из множеств A или B, поэтому:
А È В =[-3;3]
А È С= [-3;4)
В È С= (-1; 4)
А È В È С = [-3; 4)
Пересечением двух множеств A и B называется множество элементов, принадлежащих одновременно и A, и B, поэтому:
|
|
А Ç В = (-1;0]
А Ç С = (-0,5;0]
В Ç С = (-0,5;3]
А Ç В Ç С = (-0,5;0]
Относительным дополнением множества B до множества A называется множество тех элементов A, которые не являются элементами B, поэтому
А \ В = [-3;-1]
B \ A = (0;3]
A \ C = [-3;-0,5]
C \ A = (0;4)
B \ C = (-1;-0,5]
C \ B = (3;4)
(А \ В) \ С = [-3;-1]
А \ (В \ С) = [-3;-1]
Симметрической разностью двух множеств A и B называется объединение двух разностей A \ B и B \ A, а а бсолютным дополнением множества A называется множество всех элементов, не принадлежащих A, поэтому:
А Å B = (А \ В)È(В \ А)={[-3;-1], (0;3]}
А Å С = (А \ C)È(C \ А)={[-3;-0,5], (0;4)}
B Å C = (B \ C)È(C \ B)={(-1;-0,5], (3;4)}
A Å B Å C = ((AÅB)\C)È(C\(AÅB))={[-3;-1]}È{(-0,5;0],(3,4)}=
={[-3;-1],(-0,5;0],(3,4)}
 ={(-µ;-3),(0;+µ)}
={(-µ;-3),(0;+µ)}
 ={(-µ;-1],(3;+µ)}
={(-µ;-1],(3;+µ)}
 ={(-µ;-0,5],[4;+µ)}
={(-µ;-0,5],[4;+µ)}
 Декартовым (прямым) произведением двух множеств A и B называется множество всех упорядоченных пар (a,b)таких, что
Декартовым (прямым) произведением двух множеств A и B называется множество всех упорядоченных пар (a,b)таких, что  и
и  , поэтому:
, поэтому:
 | |||||
| |||||
| |||||
Задача 2. Даны отображения (числовые функции) ƒ и g. Найдите область определения и область значений отображений. Определите, являются ли они инъективными, сюрьективными или биективными в найденных областях. Найдите композицию (ƒ ◦ g), (g ◦ ƒ), обратные (слева и справа) отображения: ƒ–1, g-1, (ƒ ◦ g)-1, (g ◦ ƒ)-1. Для заданных множеств A, B Í ℝ найдите f(A), g(A),ƒ–1(B), g-1(B). Найдите также неподвижные точки отображений.
f (x) = –(x + 1)2; g (x) = – x –2; А = [–1.5; 1]; В = [–2; –1]
Решение:
область определения отображения f – это множество таких значений х, для которых имеется вещественное число у такое, что у = f (x). И, так как для любого вещественного числа х найдется число у с указанным свойством, то пр1 f =ℝ – множество всех вещественных чисел.
Аналогично, область определения отображения g: пр1 g =ℝ.
Область значений отображения f – это множество всех образов элементов х Îпр1 f. Тем самым, пр2 f ={ y Î ℝ.: y ≤ 0 } (т.к. (x + 1)2 ≥ 0 и =>–(x + 1)2 ≤ 0). А область значений отображения g – это множество всех вещественных чисел, т.е. пр2 g =ℝ.
|
|
Отображение g является инъективным, поскольку для каждого у Îпр2 g, имеется ровно один х Î пр1 g (или каждый образ имеет ровно один прообраз).
Отображение f инъективным не является, т.к. для некоторых у Îпр2 f, имеется более одного прообраза, например: для у = –1 прообразами будут х =0 и х = –2.
Отображение g является сюрьективным, поскольку для каждого у Îпр2 g, имеется хотя бы один х Îпр1 g (или каждый образ имеет хотя бы один прообраз).
Отображение f также является сюрьективным, т.к. для каждого у Îпр2 f, имеется хотя бы один х Îпр1 f такой, что у = f (x).
Так как g одновременно инъективно и сюрьективно, то оно является биективным отображением.
f неявляется биективным отображением.
Найдем композицию отображений:
(f ∘ g)(x) = f (g (x)) = –(g (x)+1)2 = –(– x –2+1)2 = –(– x –1)2 = –(x+ 1)2,
(g∘ f)(x) = g (f (x)) =– f (x)–2 = –(–(x +1)2) –2 =(x+ 1)2–2.
Отображение f обратимо справа, как сюрьекция. И  , где y ≤ 0. Из выражения y=– (x +1)2 найдем x.
, где y ≤ 0. Из выражения y=– (x +1)2 найдем x.
Тогда 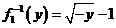 и
и  , где y ≤ 0.
, где y ≤ 0.
При этом, (f ∘ f ‑1)(у)= f (f ‑1(y)) =  – тождественное отображение при y ≤ 0.
– тождественное отображение при y ≤ 0.
Отображение g обратимо как слева, так и справа, как биекция. И  , где y любое. Из выражения
, где y любое. Из выражения 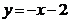 следует:
следует:  . И при этом: (g ∘ g ‑1 )(у) = g (g ‑1(y)) = –(–2– y)–2 = y
. И при этом: (g ∘ g ‑1 )(у) = g (g ‑1(y)) = –(–2– y)–2 = y
и(g ‑1∘ g)(х) = g ‑1(g(х)) = –2–(– x -2) = x – тождественные отображения.
Посвойствам композиции 
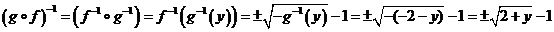
f (A) = { y = f (x), где x Î A }, поэтому f (A)=[–4; –0,25].
Аналогично, g (A) = { y = g (x), где x Î A } = [–3; –0,5].


Найдем неподвижные точки. По определению это такие х, что: f (x)= x и g (x)= x. Таким образом, x = –(x+ 1)2. Отсюда x 2+3 x +1=0 и т. к. дискриминант D =9–4=5>0, то 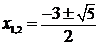 – две неподвижные точки f (x).
– две неподвижные точки f (x).
Из g (x)= x следует, что x =– x –2 и x = –1 – неподвижная точка g (x).
Задача 3. Используя таблицу истинности и аналитические преобразования, установить эквивалентность функций в формулах:
x → (y ↓ z) = (x → y) ↓ (x → z)
((x ≡ y) · (x | y)) ≡ x & y
Решение:
1. Составим таблицы истинности для функций
| x | y | z | (y ↓ z) | x → (y ↓ z) |
| x | y | z | (x → y) | (x → z) | (x → y) ↓ (x → z) |
|
|
Так как значения не совпадают, то функции не эквивалентны.
Преобразуем функции


Так как полученные выражения не равны, то функции не эквивалентны.
2. Составим таблицы истинности для функций
| x | y | x&y |
| x | y | x ≡ y | x | y | (x ≡ y) · (x | y) |
Так как значения не совпадают, то функции не эквивалентны.
Преобразуем функцию 

Так как выражения 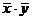 и
и  не равны, то функции не эквивалентны.
не равны, то функции не эквивалентны.
Задача 4.Определить к каким классам относится функция следующего вида: 

Решение:
| x | y | z | 
| 
| 
|
f(0,0,0) = 0 => функция принадлежит к классу Т0– классуфункций, сохраняющих 0,
f(1,1,1) ≠ 1=> функция не принадлежит кклассу Т1 – классу функций, сохраняющих 1,
f(0,0,0) ≠ 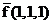 => функция не принадлежит к классуS– классу самодвойственных функций,
=> функция не принадлежит к классуS– классу самодвойственных функций,
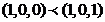 , а
, а  => функция не принадлежит к классу M – классу монотонных функций.
=> функция не принадлежит к классу M – классу монотонных функций.
Составим для функции полином Жегалкина (методом неопределенных коэффициентов):
f=c0Åc1xÅc2yÅc3zÅc12xyÅc13xzÅc23yzÅc123xyz
f(0,0,0)= c0=0
f(0,0,1)= c0Åc3=1® c3=1
f(0,1,0)= c0Åc2=1® c2=1
f(0,1,1)= c0Åc2Åc3Åc23=1® c23=1
f(1,0,0)= c0Åc1=1® c1=1
f(1,0,1)= c0Åc1Åc3Åc13=0® c13=0
f(1,1,0)= c0Åc1Åc2Åc12=1® c12=1
f(1,1,1)= c0Åc1Åc2Åc3Åc12Åc13Åc23Åc123=0® c123=1
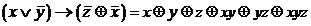
функция является линейной, если ее полином Жегалкина имеет вид:
f(x1,x2,…xn)=c0Åc1x1Åc2x2Å…Åcnxn
В нашем случае функция не приводится к такому виду => она не линейна и
не принадлежит к L– классу линейных функций.
Задача 5. Необходимо для данной функции найти её СДНФ, СКНФ, ЭСНФ, ИСНФ, принимающей значения 1 на следующих наборах:
0, 1,2,6,8,12,13,14
Решение.
Составим таблицу истинности для функции. В столбце СДНФ показаны элементарные конъюнкции, в строках, где функция принимает единичные значения, а в столбце СКНФ - элементарные дизъюнкции в строках, где функция равна нулю.
|
|
| x 1 | x 2 | x3 | x4 | f | СДНФ | СКНФ |

| ||||||

| ||||||

| ||||||

| ||||||

| ||||||
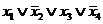
| ||||||

| ||||||

| ||||||

| ||||||

| ||||||

| ||||||

| ||||||

| ||||||

| ||||||

| ||||||

|
Тем самым, совершенная дизъюнктивная нормальная форма (СДНФ):
f(x)=  Ú
Ú  Ú
Ú  Ú
Ú  Ú
Ú  Ú
Ú  Ú
Ú  Ú
Ú  .
.
Совершенная конъюнктивная нормальная форма (СКНФ):
f(x)=( )&(
)&( )&(
)&(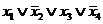 )&(
)&( )&
)&
&( )&(
)&( )&(
)&( )&(
)&( )
)
Список литературы
1 Аляев Ю.А. Тюрин С.Ф. Дискретная математика и математическая логика. — М.: Финансы и статистика, 2006. — 368 с.
2 Акимов О.Е.Дискретная математика. Логика, группы, графы. - 2-е изд.- М., Лаборатория базовых знаний, 2001. - 376 с. - "Технический университет".
3 Асанов М. О., Баранский В. А., Расин В. В. Дискретная математика: графы, матроиды, алгоритмы. - Ижевск: НИЦ «Регулярная и хаотическая динамика», 2006, 288 стр.
4 Гаврилов Г. П., Сапоженко А. А. Задачи и упражнения по дискретной математике: Учеб. пособие. — 3-е изд., перераб. — М.: ФИЗМАТЛИТ, 2005. - 416 с.
5 Яблонский С.В. Введение в дискретную математику. 4-е издание, стереотипное - М.: Высшая школа, 2005. - 484 с
Содержание
Задача 1. Для заданных множеств А, В и С найдите: 2
Задача 2. Даны отображения (числовые функции) ƒ и g.. 5
Задача 3. Используя таблицу истинности и аналитические преобразования, установить эквивалентность функций в формулах.. 8
Задача 4.Определить к каким классам относится функция…… 9
Задача 5. Необходимо для данной функции найти её СДНФ, СКНФ, ЭСНФ, ИСНФ: 10
Задача 6. Используя метод Квайна, необходимо найти МДНФ функции, принимающей значения 1 на наборах.. 11
Задача 7. Используя метод Квайна – Мак-Класки, необходимо найти МДНФ функции, принимающей. 13
Задача 8. Используя метод диаграмм Вейча, необходимо найти МДНФ функции, принимающей значение 1 15
Задача 9. Задать граф. 17
Задача 10. Определить следующие основные характеристики графа: 18
Задача 11. Определить, является ли данный граф: 19
Задача 12. Определить метрические характеристики графа. 21
Список литературы.. 23
Задача 1. Для заданных множеств А, В и С найдите:
А È В, А È С, В È С, А È В È С, А Ç В, А Ç С, В Ç С, А Ç В Ç С, A \ B, B \ A, A \ C, C \ A, B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А Å B, А Å С, B Å C, A Å B Å C. Изобразите на плоскости А ´ В, А ´ С, В ´ С. Найдите 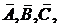 считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).
считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).
|
|
А = [-3; 0] – отрезок числовой оси
В = (-1; 3] – полуинтервал на числовой оси
С = (-0.5; 4) – интервал на числовой оси
Решение:
Объединением двух множеств A и B называется множество, состоящее из всех элементов, являющихся элементами хотя бы одного из множеств A или B, поэтому:
А È В =[-3;3]
А È С= [-3;4)
В È С= (-1; 4)
А È В È С = [-3; 4)
Пересечением двух множеств A и B называется множество элементов, принадлежащих одновременно и A, и B, поэтому:
А Ç В = (-1;0]
А Ç С = (-0,5;0]
В Ç С = (-0,5;3]
А Ç В Ç С = (-0,5;0]
Относительным дополнением множества B до множества A называется множество тех элементов A, которые не являются элементами B, поэтому
А \ В = [-3;-1]
B \ A = (0;3]
A \ C = [-3;-0,5]
C \ A = (0;4)
B \ C = (-1;-0,5]
C \ B = (3;4)
(А \ В) \ С = [-3;-1]
А \ (В \ С) = [-3;-1]
Симметрической разностью двух множеств A и B называется объединение двух разностей A \ B и B \ A, а а бсолютным дополнением множества A называется множество всех элементов, не принадлежащих A, поэтому:
А Å B = (А \ В)È(В \ А)={[-3;-1], (0;3]}
А Å С = (А \ C)È(C \ А)={[-3;-0,5], (0;4)}
B Å C = (B \ C)È(C \ B)={(-1;-0,5], (3;4)}
A Å B Å C = ((AÅB)\C)È(C\(AÅB))={[-3;-1]}È{(-0,5;0],(3,4)}=
={[-3;-1],(-0,5;0],(3,4)}
 ={(-µ;-3),(0;+µ)}
={(-µ;-3),(0;+µ)}
 ={(-µ;-1],(3;+µ)}
={(-µ;-1],(3;+µ)}
 ={(-µ;-0,5],[4;+µ)}
={(-µ;-0,5],[4;+µ)}
 Декартовым (прямым) произведением двух множеств A и B называется множество всех упорядоченных пар (a,b)таких, что
Декартовым (прямым) произведением двух множеств A и B называется множество всех упорядоченных пар (a,b)таких, что  и
и  , поэтому:
, поэтому:
 | |||||
| |||||
| |||||
Задача 2. Даны отображения (числовые функции) ƒ и g. Найдите область определения и область значений отображений. Определите, являются ли они инъективными, сюрьективными или биективными в найденных областях. Найдите композицию (ƒ ◦ g), (g ◦ ƒ), обратные (слева и справа) отображения: ƒ–1, g-1, (ƒ ◦ g)-1, (g ◦ ƒ)-1. Для заданных множеств A, B Í ℝ найдите f(A), g(A),ƒ–1(B), g-1(B). Найдите также неподвижные точки отображений.
f (x) = –(x + 1)2; g (x) = – x –2; А = [–1.5; 1]; В = [–2; –1]
Решение:
область определения отображения f – это множество таких значений х, для которых имеется вещественное число у такое, что у = f (x). И, так как для любого вещественного числа х найдется число у с указанным свойством, то пр1 f =ℝ – множество всех вещественных чисел.
Аналогично, область определения отображения g: пр1 g =ℝ.
Область значений отображения f – это множество всех образов элементов х Îпр1 f. Тем самым, пр2 f ={ y Î ℝ.: y ≤ 0 } (т.к. (x + 1)2 ≥ 0 и =>–(x + 1)2 ≤ 0). А область значений отображения g – это множество всех вещественных чисел, т.е. пр2 g =ℝ.
Отображение g является инъективным, поскольку для каждого у Îпр2 g, имеется ровно один х Î пр1 g (или каждый образ имеет ровно один прообраз).
Отображение f инъективным не является, т.к. для некоторых у Îпр2 f, имеется более одного прообраза, например: для у = –1 прообразами будут х =0 и х = –2.
Отображение g является сюрьективным, поскольку для каждого у Îпр2 g, имеется хотя бы один х Îпр1 g (или каждый образ имеет хотя бы один прообраз).
Отображение f также является сюрьективным, т.к. для каждого у Îпр2 f, имеется хотя бы один х Îпр1 f такой, что у = f (x).
Так как g одновременно инъективно и сюрьективно, то оно является биективным отображением.
f неявляется биективным отображением.
Найдем композицию отображений:
(f ∘ g)(x) = f (g (x)) = –(g (x)+1)2 = –(– x –2+1)2 = –(– x –1)2 = –(x+ 1)2,
(g∘ f)(x) = g (f (x)) =– f (x)–2 = –(–(x +1)2) –2 =(x+ 1)2–2.
Отображение f обратимо справа, как сюрьекция. И  , где y ≤ 0. Из выражения y=– (x +1)2 найдем x.
, где y ≤ 0. Из выражения y=– (x +1)2 найдем x.
Тогда 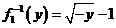 и
и  , где y ≤ 0.
, где y ≤ 0.
При этом, (f ∘ f ‑1)(у)= f (f ‑1(y)) =  – тождественное отображение при y ≤ 0.
– тождественное отображение при y ≤ 0.
Отображение g обратимо как слева, так и справа, как биекция. И  , где y любое. Из выражения
, где y любое. Из выражения 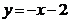 следует:
следует:  . И при этом: (g ∘ g ‑1 )(у) = g (g ‑1(y)) = –(–2– y)–2 = y
. И при этом: (g ∘ g ‑1 )(у) = g (g ‑1(y)) = –(–2– y)–2 = y
и(g ‑1∘ g)(х) = g ‑1(g(х)) = –2–(– x -2) = x – тождественные отображения.
Посвойствам композиции 
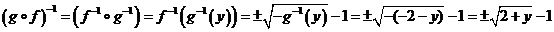
f (A) = { y = f (x), где x Î A }, поэтому f (A)=[–4; –0,25].
Аналогично, g (A) = { y = g (x), где x Î A } = [–3; –0,5].


Найдем неподвижные точки. По определению это такие х, что: f (x)= x и g (x)= x. Таким образом, x = –(x+ 1)2. Отсюда x 2+3 x +1=0 и т. к. дискриминант D =9–4=5>0, то 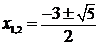 – две неподвижные точки f (x).
– две неподвижные точки f (x).
Из g (x)= x следует, что x =– x –2 и x = –1 – неподвижная точка g (x).
Задача 3. Используя таблицу истинности и аналитические преобразования, установить эквивалентность функций в формулах:
x → (y ↓ z) = (x → y) ↓ (x → z)
((x ≡ y) · (x | y)) ≡ x & y
Решение:
1. Составим таблицы истинности для функций
| x | y | z | (y ↓ z) | x → (y ↓ z) |
| x | y | z | (x → y) | (x → z) | (x → y) ↓ (x → z) |
Так как значения не совпадают, то функции не эквивалентны.
Преобразуем функции


Так как полученные выражения не равны, то функции не эквивалентны.
2. Составим таблицы истинности для функций
| x | y | x&y |
| x | y | x ≡ y | x | y | (x ≡ y) · (x | y) |
Так как значения не совпадают, то функции не эквивалентны.
Преобразуем функцию 

Так как выражения 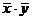 и
и  не равны, то функции не эквивалентны.
не равны, то функции не эквивалентны.
Задача 4.Определить к каким классам относится функция следующего вида: 

Решение:
| x | y | z | 
| 
| 
|
f(0,0,0) = 0 => функция принадлежит к классу Т0– классуфункций, сохраняющих 0,
f(1,1,1) ≠ 1=> функция не принадлежит кклассу Т1 – классу функций, сохраняющих 1,
f(0,0,0) ≠ 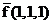 => функция не принадлежит к классуS– классу самодвойственных функций,
=> функция не принадлежит к классуS– классу самодвойственных функций,
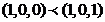 , а
, а  => функция не принадлежит к классу M – классу монотонных функций.
=> функция не принадлежит к классу M – классу монотонных функций.
Составим для функции полином Жегалкина (методом неопределенных коэффициентов):
f=c0Åc1xÅc2yÅc3zÅc12xyÅc13xzÅc23yzÅc123xyz
f(0,0,0)= c0=0
f(0,0,1)= c0Åc3=1® c3=1
f(0,1,0)= c0Åc2=1® c2=1
f(0,1,1)= c0Åc2Åc3Åc23=1® c23=1
f(1,0,0)= c0Åc1=1® c1=1
f(1,0,1)= c0Åc1Åc3Åc13=0® c13=0
f(1,1,0)= c0Åc1Åc2Åc12=1® c12=1
f(1,1,1)= c0Åc1Åc2Åc3Åc12Åc13Åc23Åc123=0® c123=1
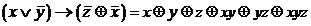
функция является линейной, если ее полином Жегалкина имеет вид:
f(x1,x2,…xn)=c0Åc1x1Åc2x2Å…Åcnxn
В нашем случае функция не приводится к такому виду => она не линейна и
не принадлежит к L– классу линейных функций.
Задача 5. Необходимо для данной функции найти её СДНФ, СКНФ, ЭСНФ, ИСНФ, принимающей значения 1 на следующих наборах:
0, 1,2,6,8,12,13,14
Решение.
Составим таблицу истинности для функции. В столбце СДНФ показаны элементарные конъюнкции, в строках, где функция принимает единичные значения, а в столбце СКНФ - элементарные дизъюнкции в строках, где функция равна нулю.
| x 1 | x 2 | x3 | x4 | f | СДНФ | СКНФ |

| ||||||

| ||||||

| ||||||

| ||||||

| ||||||
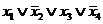
| ||||||

| ||||||

| ||||||

| ||||||

| ||||||

| ||||||

| ||||||

| ||||||

| ||||||

| ||||||

|
Тем самым, совершенная дизъюнктивная нормальная форма (СДНФ):
f(x)=  Ú
Ú  Ú
Ú  Ú
Ú  Ú
Ú  Ú
Ú  Ú
Ú  Ú
Ú  .
.
Совершенная конъюнктивная нормальная форма (СКНФ):
f(x)=( )&(
)&( )&(
)&(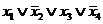 )&(
)&( )&
)&
&( )&(
)&( )&(
)&( )&(
)&( )
)
Задача 6. Используя метод Квайна, необходимо найти МДНФ функции, принимающей значения 1 на наборах: 1,3,5,7,11,12.
Решение:
| Таблица 1 | |||||
| x1 | x2 | x3 | x4 | f | Минтермы |

| |||||

| |||||

| |||||

| |||||

| |||||

| |||||
1. Составляем таблицу 1 истинности, по которой записываются все минтермы.
2.
Составляем таблицу 2.
| Таблица 2 | ||
| Термы 4 ранга | Термы 3 ранга | Термы 2 ранга |
 * *
|  * *
| 
|
 * *
|  * *
| 
|
 * *
|  * *
| |
 * *
| 
| |
 * *
| 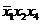 * *
| |
|
|
|

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!