Рассмотрим, какую роль играют определители n –го порядка в решении системы n линейных уравнений с n неизвестными и вычислении обратной матрицы. Предварительно докажем следующие две теоремы.
Теорема 1: Какую бы строку (столбец) определителя  n –го порядка мы ни взяли, определитель
n –го порядка мы ни взяли, определитель  всегда равен сумме произведений элементов этой строки (столбца) на их алгебраические дополнения.
всегда равен сумме произведений элементов этой строки (столбца) на их алгебраические дополнения.
Иными словами, имеет место такое разложение определителя  по элементам строки или столбца:
по элементам строки или столбца:
 (1) или
(1) или
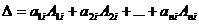 (2).
(2).
Доказательство: В силу свойства равноправности строк и столбцов можно ограничиться выводом разложения (1). По свойству 6, (§ 3)

по теореме 2 (из предыдущего параграфа). Что и требовалось доказать.
Пример:

Теорема 2: Сумма произведений элементов какой-нибудь строки (столбца) на алгебраические дополнения соответствующих элементов другой строки (столбца) определителя равна нулю.
Иными словами: 
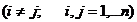 ,
,

 .
.
Кроме данного определителя рассмотрим вспомогательный  , у которого
, у которого  -я и
-я и 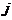 -я строки одинаковы, а все строки, за исключением
-я строки одинаковы, а все строки, за исключением  -й и
-й и 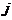 -й, совпадают с соответствующими строками определителя
-й, совпадают с соответствующими строками определителя  .
.

Он по свойству 3 из § 3 равен 0, с другой стороны, разлагая  по элементам
по элементам 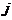 - й строки, получим: (3)
- й строки, получим: (3)  ,
,
где  - алгебраические дополнения элементов
- алгебраические дополнения элементов 
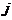 -й строки определителя
-й строки определителя  . При составлении алгебраического дополнения
. При составлении алгебраического дополнения  мы вычеркиваем в
мы вычеркиваем в 
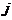 -ю строку (и
-ю строку (и  -й столбец), т.е. вычеркиваем единственную строку, отличающую
-й столбец), т.е. вычеркиваем единственную строку, отличающую  от
от  .Следовательно,
.Следовательно,  , где
, где  - алгебраическое дополнение элемента
- алгебраическое дополнение элемента 
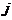 -й строки определителя
-й строки определителя  . Таким образом, равенство (3) принимает следующий окончательный вид:
. Таким образом, равенство (3) принимает следующий окончательный вид: 
Справедливость теоремы для столбцов очевидна в силу свойства равноправности строк и столбцов.
Обратная матрица
Определение 1: Квадратная матрица называется вырожденной (или особенной), если ее определитель равен нулю, и невырожденной (или неособенной), если ее определитель отличен от нуля.
Произведение матриц, хотя бы одна из которых вырожденная, вновь вырожденная матрица.
Роль единицы в умножении матриц играет единичная матрица  , причем она перестановочная с любой матрицей
, причем она перестановочная с любой матрицей  данного порядка,
данного порядка,  (доказывается это равенство непосредственным применением правила умножения матриц).
(доказывается это равенство непосредственным применением правила умножения матриц).
Рассмотрим вопрос о существовании для данной матрицы  обратной матрицы. Ввиду некоммутативности умножения матриц, мы будем говорить о правой обратной матрице, т.е. о такой матрице
обратной матрицы. Ввиду некоммутативности умножения матриц, мы будем говорить о правой обратной матрице, т.е. о такой матрице  , что произведение матрицы
, что произведение матрицы  справа на эту матрицу дает единичную матрицу
справа на эту матрицу дает единичную матрицу
 (1).
(1).
Если матрица  вырожденная, то если бы матрица
вырожденная, то если бы матрица  существовала, произведение, стоящее в правой части равенства (2), было бы, как мы знаем, вырожденной матрицей, в то время как на самом деле матрица
существовала, произведение, стоящее в правой части равенства (2), было бы, как мы знаем, вырожденной матрицей, в то время как на самом деле матрица 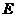 , стоящая в правой части этого равенства, является невырожденной, т.к. ее определитель равен единице. Таки образом, вырожденная матрица не может иметь правой обратной матрицы. Такие же соображения показывают, что она не имеет и левой обратной и поэтому для вырожденной матрицы обратная матрица вообще не существует.
, стоящая в правой части этого равенства, является невырожденной, т.к. ее определитель равен единице. Таки образом, вырожденная матрица не может иметь правой обратной матрицы. Такие же соображения показывают, что она не имеет и левой обратной и поэтому для вырожденной матрицы обратная матрица вообще не существует.
Рассмотрим случай с невырожденной матрицей; для этого введем следующие вспомогательные понятия. Пусть дана матрица  -го порядка
-го порядка
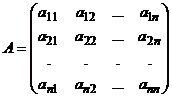 и
и  .
.
Матрица  составлена из алгебраических дополнений к элементам матрицы
составлена из алгебраических дополнений к элементам матрицы  , причем алгебраическое дополнение к элементу
, причем алгебраическое дополнение к элементу  стоит на пересечении
стоит на пересечении 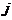 -й строки и
-й строки и  -го столбца. Эту матрицу назовем присоединенной матрицей к матрице
-го столбца. Эту матрицу назовем присоединенной матрицей к матрице  .
.
Найдем произведения  и
и  . Используя известную теорему о разложении определителя по строке или столбцу, а также теорему о сумме произведений элементов любой строки или столбца на алгебраические дополнения к соответствующим элементам другой строки или столбца и обозначая через
. Используя известную теорему о разложении определителя по строке или столбцу, а также теорему о сумме произведений элементов любой строки или столбца на алгебраические дополнения к соответствующим элементам другой строки или столбца и обозначая через  определитель матрицы
определитель матрицы  .
.
 , мы получим:
, мы получим:
 (2).
(2).
Отсюда вытекает, что если матрица  невырожденная, то ее присоединенная матрица
невырожденная, то ее присоединенная матрица  также будет невырожденной, причем определитель
также будет невырожденной, причем определитель  матрицы
матрицы  равен
равен 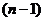 -й степени определителя
-й степени определителя  матрицы
матрицы  . В самом деле, из равенства (2), если перейдем к определителям, то получим:
. В самом деле, из равенства (2), если перейдем к определителям, то получим:  , откуда ввиду
, откуда ввиду  .
.
Теперь легко доказать существование обратной матрицы для всякой невырожденной матрицы  и найти ее вид. Заметим сначала, что если мы рассмотрим произведение двух матриц
и найти ее вид. Заметим сначала, что если мы рассмотрим произведение двух матриц 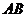 и все элементы одного из множителей, например
и все элементы одного из множителей, например  , разделим на одно и то же число
, разделим на одно и то же число  , то все элементы произведения
, то все элементы произведения 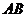 также разделятся на это число: для доказательства нужно лишь вспомнить определение умножения матриц. Таким образом, если
также разделятся на это число: для доказательства нужно лишь вспомнить определение умножения матриц. Таким образом, если  , то из равенства (2) вытекает, что обратной для матрицы
, то из равенства (2) вытекает, что обратной для матрицы  будет служить матрица, получающаяся из присоединенной матрицы
будет служить матрица, получающаяся из присоединенной матрицы  делением всех ее элементов на число
делением всех ее элементов на число  :
:
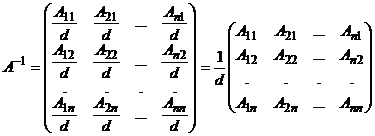 .
.
Действительно, из (2) вытекают равенства  (3).
(3).
Можно показать, что  определяется однозначно.
определяется однозначно.
Пример: 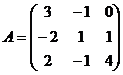 ,
, 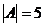 ,
,  .
.


 =
=  = E
= E
Правило Крамера
Рассмотрим систему (4) n линейных уравнений с n неизвестными. Составим определитель  из коэффициентов при неизвестных системы (4); его называют определителем системы. Покажем, как при помощи теоремы 1 и теоремы 2 можно решить при
из коэффициентов при неизвестных системы (4); его называют определителем системы. Покажем, как при помощи теоремы 1 и теоремы 2 можно решить при 
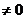 систему уравнений
систему уравнений
(4)  .
.
Перейдём к матричной записи системы (4):  (5), где
(5), где  ,
,  ,
, 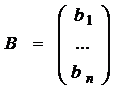 .
.
Если  , то существует обратная матрица
, то существует обратная матрица  . Покажем, что матрица
. Покажем, что матрица  - единственное решение системы (4). Действительно,
- единственное решение системы (4). Действительно,
 ,
,
т.е.  - решение уравнения (5), а значит и системы (4).
- решение уравнения (5), а значит и системы (4).
Если  - какое – то решение уравнения (5), то
- какое – то решение уравнения (5), то  . Тогда
. Тогда  .
.
Следовательно, матрица  - единственное решение уравнения (5) и системы (4).
- единственное решение уравнения (5) и системы (4).
Наряду с определителем  рассмотрим определители
рассмотрим определители 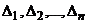 , где
, где  получается из
получается из  заменой
заменой  - го столбца столбцом из свободных членов:
- го столбца столбцом из свободных членов:  . Раскладывая определитель
. Раскладывая определитель  ,
,  , по
, по  - му столбцу, получаем:
- му столбцу, получаем:
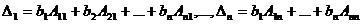 . Выясним, как же выглядит матрица
. Выясним, как же выглядит матрица  . Так как
. Так как  , тогда
, тогда
 .
.
Тогда  . Эти формулы называют формулами Крамера.
. Эти формулы называют формулами Крамера.
Таким образом, мы доказали теорему:
Теорема: Если определитель  системы
системы  линейных уравнений с
линейных уравнений с  неизвестными отличен от 0, то система имеет единственное решение, выражаемое формулами:
неизвестными отличен от 0, то система имеет единственное решение, выражаемое формулами:  .
.



 n –го порядка мы ни взяли, определитель
n –го порядка мы ни взяли, определитель  (1) или
(1) или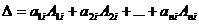 (2).
(2).


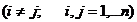 ,
,
 .
. , у которого
, у которого  -я и
-я и 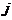 -я строки одинаковы, а все строки, за исключением
-я строки одинаковы, а все строки, за исключением 
 ,
, - алгебраические дополнения элементов
- алгебраические дополнения элементов 
 мы вычеркиваем в
мы вычеркиваем в  -й столбец), т.е. вычеркиваем единственную строку, отличающую
-й столбец), т.е. вычеркиваем единственную строку, отличающую  , где
, где  - алгебраическое дополнение элемента
- алгебраическое дополнение элемента  , причем она перестановочная с любой матрицей
, причем она перестановочная с любой матрицей  данного порядка,
данного порядка,  (доказывается это равенство непосредственным применением правила умножения матриц).
(доказывается это равенство непосредственным применением правила умножения матриц). , что произведение матрицы
, что произведение матрицы  (1).
(1).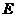 , стоящая в правой части этого равенства, является невырожденной, т.к. ее определитель равен единице. Таки образом, вырожденная матрица не может иметь правой обратной матрицы. Такие же соображения показывают, что она не имеет и левой обратной и поэтому для вырожденной матрицы обратная матрица вообще не существует.
, стоящая в правой части этого равенства, является невырожденной, т.к. ее определитель равен единице. Таки образом, вырожденная матрица не может иметь правой обратной матрицы. Такие же соображения показывают, что она не имеет и левой обратной и поэтому для вырожденной матрицы обратная матрица вообще не существует. -го порядка
-го порядка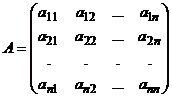 и
и  .
. составлена из алгебраических дополнений к элементам матрицы
составлена из алгебраических дополнений к элементам матрицы  стоит на пересечении
стоит на пересечении  и
и  . Используя известную теорему о разложении определителя по строке или столбцу, а также теорему о сумме произведений элементов любой строки или столбца на алгебраические дополнения к соответствующим элементам другой строки или столбца и обозначая через
. Используя известную теорему о разложении определителя по строке или столбцу, а также теорему о сумме произведений элементов любой строки или столбца на алгебраические дополнения к соответствующим элементам другой строки или столбца и обозначая через  определитель матрицы
определитель матрицы  , мы получим:
, мы получим: (2).
(2). матрицы
матрицы 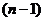 -й степени определителя
-й степени определителя  , откуда ввиду
, откуда ввиду  .
.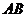 и все элементы одного из множителей, например
и все элементы одного из множителей, например  , разделим на одно и то же число
, разделим на одно и то же число  , то из равенства (2) вытекает, что обратной для матрицы
, то из равенства (2) вытекает, что обратной для матрицы 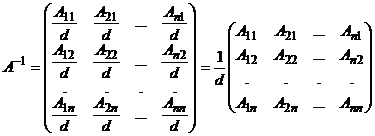 .
. (3).
(3).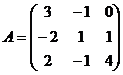 ,
, 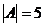 ,
,  .
.

 =
=  = E
= E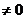 систему уравнений
систему уравнений .
. (5), где
(5), где  ,
,  ,
, 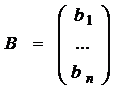 .
. , то существует обратная матрица
, то существует обратная матрица  - единственное решение системы (4). Действительно,
- единственное решение системы (4). Действительно, ,
, - какое – то решение уравнения (5), то
- какое – то решение уравнения (5), то  . Тогда
. Тогда  .
. рассмотрим определители
рассмотрим определители 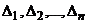 , где
, где  получается из
получается из  . Раскладывая определитель
. Раскладывая определитель  , по
, по 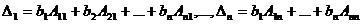 . Выясним, как же выглядит матрица
. Выясним, как же выглядит матрица  . Так как
. Так как  , тогда
, тогда .
. . Эти формулы называют формулами Крамера.
. Эти формулы называют формулами Крамера.


