П. 18. 4. Замена переменной в двойном интеграле.
Пусть требуется найти интеграл

Предположим, что фигура А связана взаимно однозначно с фигурой В плоскости u u при помощи формул
x = x (u, u), y = y (u, u). (1)
Будем предполагать, что у функций x (u, u), y (u, u) существуют непрерывные частные производные по u и u. Тогда формула замены переменных в двойном интеграле запишется в виде
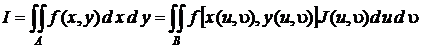 , (2)
, (2)
где J (u, u) − абсолютная величина якобиана

а J (u, u) d u d u − элемент площади криволинейных координат.
Если, в частности, преобразование состоит в переходе к полярным координатам, то формула (2) примет вид
 . (3)
. (3)
При этом надо помнить, что для правой части формулы (3) числа r и q суть уже не декартовы, а полярные координаты точек фигуры А.
Тройной интеграл. Основные понятия.
Тройной интеграл является аналогом двойного интеграла и вводится для функции трех переменных.
Определение.
Пусть в замкнутой области V пространства Oxyz задана непрерывная функция U = f (x, y, z). Разобьем область V на п произвольных областей, не имеющих общих внутренних точек, с объемами  . В каждой области возьмем произвольную точку M (xi, yi, zi) и составим сумму
. В каждой области возьмем произвольную точку M (xi, yi, zi) и составим сумму
 , (1)
, (1)
которая называется интегральной суммой для функции f (x, y, z) по области V. Обозначим через d наибольший диаметр частичных областей.
Определение. Если интегральная сумма (1) при d ® 0 имеет предел, то этот предел называется тройным интегралом от функции f (x, y, z) по области V и обозначается символом
 ,
,
где dV = dx dy dz – элемент объема.
В этом случае f (x, y, z) называется интегрируемой в области V; V – областью интегрирования, х, у, z – переменными интегрирования.
Теорема (существования). Если функция U = f (x, y, z) непрерывна в ограниченной замкнутой области V, то предел интегральной суммы (1) при п ® ¥ и  существует и не зависит ни от способа разбиения области V на части ни о выбора точек M (xi, yi, zi) в них.
существует и не зависит ни от способа разбиения области V на части ни о выбора точек M (xi, yi, zi) в них.
Свойства тройного интеграла:
1)  , с = const.
, с = const.
2)  .
.
3)  , где V = V 1 È V 2,
, где V = V 1 È V 2,
а пересечение V 1 и V 2 состоит из границы, их разделяющей.
4) Если f (x, y, z) ³ 0 Þ  .
.
Если f (x, y, z) ³ φ (x, y, z) Þ 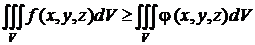 .
.
5) 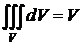 , где V – объем тела.
, где V – объем тела.
6) 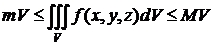 , где т, М – соответственно наименьшее и наибольшее значения функции f в области V.
, где т, М – соответственно наименьшее и наибольшее значения функции f в области V.
7) Теорема (о среднем значении). Если функция f (x, y, z) непрерывна в замкнутой области V, то в этой области существует такая точка (x 0, y 0, z 0), что
 ,
,
где V – объем тела.
П. 19.2. Замена переменных в тройном интеграле.
Вычисление тройного интеграла в цилиндрических и
Сферических координатах.
Пусть требуется найти интеграл

Предположим, что тело А, находящееся в пространстве xyz, связано взаимно однозначно с телом В, находящимся в пространстве u uv, при помощи формул
x = x (u, u, v), y = y (u, u, v), z = z (u, u, v). (1)
Будем предполагать, что у функций x (u, u, v), y (u, u, v), z (u, u, v) существуют непрерывные частные производные по u, u, v. Тогда формула замены переменных в тройном интеграле запишется в виде
 , (2)
, (2)
где u, u, v − криволинейные координаты точки (x, y, z), J (u, u, v) − абсолютная величина якобиана
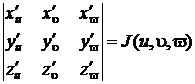
На практике часто встречаются два вида координат (x, y, z).
I. Цилиндрические координаты. Цилиндрическими координатами точки (x, y, z) называются числа r, j, z, где r и j − полярные координаты точки (x, y).
Ясно, что здесь
x = r cos j, y = r sin j, z = z
и потому якобиан этого преобразования

Стало быть, при переходе к цилиндрическим координатам общая формула (2) примет вид
 . (3)
. (3)
II. Сферические координаты. Сферическими координатам точки М (x, y, z) называются числа r, q, j, где q − угол между осью Оz и радиусом-вектором 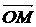 точки М, r − длина этого радиус-вектора, т. е. расстояние между началом координат О и точкой М, а j − двугранный угол между полуплоскостью с ребром Oz, содержащей положительную часть оси Ох, и точку М. Из рисунка видно, что
точки М, r − длина этого радиус-вектора, т. е. расстояние между началом координат О и точкой М, а j − двугранный угол между полуплоскостью с ребром Oz, содержащей положительную часть оси Ох, и точку М. Из рисунка видно, что
OP = r sin q.
Так как х и у − проекции  на оси Ох и Оу, а z − проекция
на оси Ох и Оу, а z − проекция 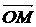 на ось Oz, то
на ось Oz, то
 . (4)
. (4)
Полезно отметить также очевидное соотношение r 2 = x 2 + y 2 + z 2.
Соответствие, даваемое формулами (4), не взаимно однозначно. Чтобы получить все пространство xyz, достаточно изменять точку (r, q, j) в области, определяемой неравенствами
0 ≤ r < + ¥, 0 ≤ q ≤ p, 0 ≤ j ≤ 2p,
но и при этом ограничении мы добиваемся взаимной однозначности, так как плоскости r = 0 пространства r qj в пространстве xyz отвечает одна точка (0, 0, 0), а точками (r, 0, 0) и (r, q,2p) отвечает одна и та же точка (r sinq, 0, r cosq). Связанные с этими нарушениями взаимной однозначности осложнения не мешают, однако, применимости к нашему случаю общей формулы (2). Мы примем это без доказательства.
Якобиан в этом случае будет равен

Тогда формула (2) примет вид
 .(5)
.(5)
Этой формулой удобно пользоваться тогда, когда f (x, y, z) имеет форму f (x 2 + y 2 + z 2), а также когда областью А служит шар x 2 + y 2 + z 2 ≤ R 2 или какая-нибудь простая часть такого шара и т. п.
Пример. Найти
 ,
,
если А − шар x 2 + y 2 + z 2 ≤ 1.
По формуле (5)
 .
.
Переходя к повторному интегралу, получаем
 .
.
Опуская простые пояснения, находим

Криволинейные интегралы.
Определение. 1. Пусть в декартовых координатах x, y, z в каждой точке M (x, y, z) кривой L задан вектор F, т. е. задана векторная функция F (M) точек M Î L, и определен единичный вектор  (М) касательной к этой кривой.
(М) касательной к этой кривой.
Разобьем кривую L на п частей; Δℓ i − длины отрезков разбиения (i = 1, 2, ¼, п). Внутри каждого отрезка разбиения произвольно возьмем точку Мi и вычислим в ней вектор F (Mi) и орт касательной  (Мi). Вычислим скалярное произведение F (Mi) ∙
(Мi). Вычислим скалярное произведение F (Mi) ∙  (Мi) и составим сумму
(Мi) и составим сумму
 (1)
(1)
которую назовем интегральной суммой векторной функции F (M) на кривой L.
Пусть l − длина наибольшего из элементов Δℓ i.
Если существует предел интегральной суммы (1) при n ® ¥ и l ® 0, то этот предел называется криволинейным интегралом и обозначается
 .
.
Таким образом,
 . (2)
. (2)
Определение 2. Так как скалярное произведение F (M) e (M) = f (M) − скалярная функция точек М кривой L, то равенство (2) может быть преобразовано в равенство
 , (3)
, (3)
левая часть которого называется криволинейным интегралом I − рода (или криволинейным интегралом по длине дуги кривой).
Определение 3. В декартовом базисе i, j, k, ассоциированном с принятой здесь системой декартовых координат, векторная функция F (M) и орт касательной e (M) задаются в виде

где P (M), Q (M), R (M) − скалярные функции точке М кривой L; a, b, g − углы, образуемые касательной к L в точках M Î L с осями координат x, y, z соответственно. Скалярное произведение этих векторов
F (M)∙ e (M) = P (M)∙cos a + Q (M)∙cos b + R (M)∙cos g. (4)
Пусть Δ x, Δ y, Δ z − проекции отрезка Δℓ на координатные оси. Тогда
Δ x = Δℓ∙cos a, Δ y = Δℓ∙cos b, Δ z = Δℓ∙cos g. (5)
Равенства (4), (5) позволяют записать
F (M)∙ e (M)∙Δℓ = P (M)∙Δ х + Q (M)∙Δ у + R (M)∙Δ z. (6)
С учетом этого равенство (2) преобразуется к виду
 . (7)
. (7)
Левая часть этого равенства называется криволинейным интегралом второго рода (или криволинейным интегралом по координатам).
Обратим внимание, что все три типа криволинейных интегралов (2), (3), (7) связаны друг с другом.
П. 20.4. Формула Грина.
Определение. Замкнутая область называется простой, если ее граница пересекается с прямыми, параллельными декартовым осям координат, не более чем в двух точках.
Рис. 1 Рис. 2
Теорема 1. Если G − простая область, ограниченная контуром L, и P (x, y), Q (x, y) − непрерывные с непрерывными частными производными функции в G, включая точки М Î L, то справедливо равенство
 . (1)
. (1)
называемое формулой Грина.
Определение. Плоская область G называется односвязной, если любой замкнутый контур L, целиком лежащий в G, ограничивает область, целиком принадлежащую области G.
Образно говоря, в односвязной области нет «дыр».
Теорема 2. Площадь А односвязной области G (рис. 1), ограниченной замкнутым контуром L, в декартовых координатах х и у определяется формулой
 (2)
(2)
От пути интегрирования.
Теорема 1. Если для любой замкнутой кривой L, целиком лежащей в односвязной области G, выполняется равенство
 , (1)
, (1)
то для любых точек А, В Î G интеграл
 (2)
(2)
не зависит от формы пути интегрирования, а зависит только от расположения точек начала А и конца В пути интегрирования.
Теорема 2. Если во всех точках односвязной области G непрерывные и дифференцируемые функции P (x, y), Q (x, y) связанные равенством
 , (3)
, (3)
то интеграл (2) не зависит в G от пути интегрирования, а зависит от точек начала и конца пути интегрирования.
Теорема 3. Если в односвязной области G определена непрерывная и дважды дифференцируемая функция U (x, y) такая, что во всех точках G выполняются равенства
 , (4)
, (4)
т. е. подынтегральная функция в (2) является полным дифференциалом функции U (x, y):
P d x + Q d y = d U,
то интеграл (2) не зависит от пути интегрирования, а зависит от точек начала и конца пути интегрирования.
Теорема 4. Если интеграл (2) в односвязной области G не зависит от пути интегрирования и А (хА, уА) Î G, B (xB, yB) Î G, то справедлива формула
 . (5)
. (5)
Темы: Поверхностные интегралы (первого и второго рода), Интегральные теоремы математического анализа и элементы теории поля на самостоятельную разработку.
п. 18. 4. Замена переменной в двойном интеграле.
Пусть требуется найти интеграл

Предположим, что фигура А связана взаимно однозначно с фигурой В плоскости u u при помощи формул
x = x (u, u), y = y (u, u). (1)
Будем предполагать, что у функций x (u, u), y (u, u) существуют непрерывные частные производные по u и u. Тогда формула замены переменных в двойном интеграле запишется в виде
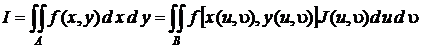 , (2)
, (2)
где J (u, u) − абсолютная величина якобиана

а J (u, u) d u d u − элемент площади криволинейных координат.
Если, в частности, преобразование состоит в переходе к полярным координатам, то формула (2) примет вид
 . (3)
. (3)
При этом надо помнить, что для правой части формулы (3) числа r и q суть уже не декартовы, а полярные координаты точек фигуры А.
Тройной интеграл. Основные понятия.
Тройной интеграл является аналогом двойного интеграла и вводится для функции трех переменных.
Определение.
Пусть в замкнутой области V пространства Oxyz задана непрерывная функция U = f (x, y, z). Разобьем область V на п произвольных областей, не имеющих общих внутренних точек, с объемами  . В каждой области возьмем произвольную точку M (xi, yi, zi) и составим сумму
. В каждой области возьмем произвольную точку M (xi, yi, zi) и составим сумму
 , (1)
, (1)
которая называется интегральной суммой для функции f (x, y, z) по области V. Обозначим через d наибольший диаметр частичных областей.
Определение. Если интегральная сумма (1) при d ® 0 имеет предел, то этот предел называется тройным интегралом от функции f (x, y, z) по области V и обозначается символом
 ,
,
где dV = dx dy dz – элемент объема.
В этом случае f (x, y, z) называется интегрируемой в области V; V – областью интегрирования, х, у, z – переменными интегрирования.
Теорема (существования). Если функция U = f (x, y, z) непрерывна в ограниченной замкнутой области V, то предел интегральной суммы (1) при п ® ¥ и  существует и не зависит ни от способа разбиения области V на части ни о выбора точек M (xi, yi, zi) в них.
существует и не зависит ни от способа разбиения области V на части ни о выбора точек M (xi, yi, zi) в них.
Свойства тройного интеграла:
1)  , с = const.
, с = const.
2)  .
.
3)  , где V = V 1 È V 2,
, где V = V 1 È V 2,
а пересечение V 1 и V 2 состоит из границы, их разделяющей.
4) Если f (x, y, z) ³ 0 Þ  .
.
Если f (x, y, z) ³ φ (x, y, z) Þ 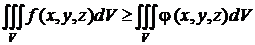 .
.
5) 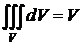 , где V – объем тела.
, где V – объем тела.
6) 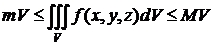 , где т, М – соответственно наименьшее и наибольшее значения функции f в области V.
, где т, М – соответственно наименьшее и наибольшее значения функции f в области V.
7) Теорема (о среднем значении). Если функция f (x, y, z) непрерывна в замкнутой области V, то в этой области существует такая точка (x 0, y 0, z 0), что
 ,
,
где V – объем тела.




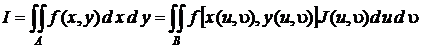 , (2)
, (2)
 . (3)
. (3) . В каждой области возьмем произвольную точку M (xi, yi, zi) и составим сумму
. В каждой области возьмем произвольную точку M (xi, yi, zi) и составим сумму , (1)
, (1) ,
, существует и не зависит ни от способа разбиения области V на части ни о выбора точек M (xi, yi, zi) в них.
существует и не зависит ни от способа разбиения области V на части ни о выбора точек M (xi, yi, zi) в них. , с = const.
, с = const. .
. , где V = V 1 È V 2,
, где V = V 1 È V 2, .
.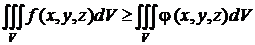 .
.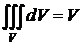 , где V – объем тела.
, где V – объем тела.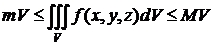 , где т, М – соответственно наименьшее и наибольшее значения функции f в области V.
, где т, М – соответственно наименьшее и наибольшее значения функции f в области V. ,
,
 , (2)
, (2)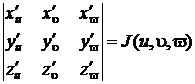

 . (3)
. (3)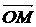 точки М, r − длина этого радиус-вектора, т. е. расстояние между началом координат О и точкой М, а j − двугранный угол между полуплоскостью с ребром Oz, содержащей положительную часть оси Ох, и точку М. Из рисунка видно, что
точки М, r − длина этого радиус-вектора, т. е. расстояние между началом координат О и точкой М, а j − двугранный угол между полуплоскостью с ребром Oz, содержащей положительную часть оси Ох, и точку М. Из рисунка видно, что на оси Ох и Оу, а z − проекция
на оси Ох и Оу, а z − проекция  . (4)
. (4)
 .(5)
.(5) ,
, .
. .
.
 (М) касательной к этой кривой.
(М) касательной к этой кривой. (1)
(1) .
. . (2)
. (2) , (3)
, (3)
 . (7)
. (7)

 . (1)
. (1) (2)
(2) , (1)
, (1) (2)
(2) , (3)
, (3) , (4)
, (4) . (5)
. (5)

