

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...
Топ:
Оснащения врачебно-сестринской бригады.
Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров...
Интересное:
Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории...
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Модуль 1.
МЕХАНИКА И СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСИ
Лекция 1
В данной лекции рассматривается механическое движение материальных тел и происходящие при этом взаимодействия между ними. Под механическим движением понимают изменение с течением времени взаимного положения тел в пространстве. Для строгости и удобства изложения материала применяют две модели твердых тел – материальная точка (м.т.) – тело, размерами которого можно пренебречь в условиях данного движения, и абсолютно твердое тело (а. т. т) - это абсолютно недеформируемое тело или тело, расстояние между двумя любыми точками которого остается постоянным при его движении.
Линию, по которой движется тело, называют траекторией движения. Для м. т. траекторию движения можно представить в виде сложения двух видов движений – по прямой линии и по окружности или как движение по окружностям разных радиусов R от нуля до бесконечности (R → ∞ соответствует прямолинейному движению, рис.1.1а).

Рис.1.1
Для а.т.т. вводят два понятия: поступательное движени е – это такое движение, при котором любая прямая, проведенная в теле, перемещается параллельно самой себе (рис.1.1,б), и вращательное движение вокруг неподвижной оси – это такое движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения (она может находиться вне тела, рис.1.1,в).
Любое движение а.т.т. можно свести к сумме двух движений - поступательного и вращательного движений. При поступательном движении а.т.т. все его точки движутся по одинаковым траекториям (рис.1.1,б), поэтому можно заменить такое движение а.т.т. на движение одной м.т. – его центра масс (его определение будет в параграфе 1.2.4). Следовательно, поступательное движение а.т.т. не требует отдельного рассмотрения наряду с изучением движения м.т.
|
|
Мгновенное ускорение м.т. Касательное и нормальное
Ускорения м.т.
Быстроту изменения скорости оценивают, вводя понятие мгновенного ускорения 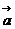 - ускорения в данной точке траектории, равного первой производной от скорости
- ускорения в данной точке траектории, равного первой производной от скорости 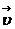 по времени t или второй производной от радиус–вектора
по времени t или второй производной от радиус–вектора 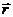 (или перемещения
(или перемещения 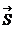 ) по времени t
) по времени t
 (1.5)
(1.5)
Проекцию вектора ускорения 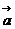 на направление касательной к траектории называют касательным (тангенциальным) ускорением
на направление касательной к траектории называют касательным (тангенциальным) ускорением  , а на направление, перпендикулярное к касательной, – нормальным (центростремительным) ускорением
, а на направление, перпендикулярное к касательной, – нормальным (центростремительным) ускорением 
 ;
; 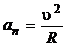 ; (1.6)
; (1.6)
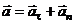 ;
; 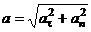 ; (1.7)
; (1.7)
где 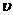 - численное значение скорости;
- численное значение скорости; 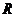 - радиус кривизны траектории в данной ее точке, он равен радиусу окружности
- радиус кривизны траектории в данной ее точке, он равен радиусу окружности 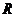 , вписанной в малый участок траектории вблизи этой точки (рис.1.3,в).
, вписанной в малый участок траектории вблизи этой точки (рис.1.3,в).
Касательное ускорение характеризует изменение скорости тела по ее численной величине (по модулю скорости), а нормальное ускорение – по направлению.
Приведем вывод формул (1.6) для ускорений 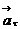 и
и  . Для этого возьмем на траектории две близко расположенные точки 1 и 2, разделенные интервалом времени
. Для этого возьмем на траектории две близко расположенные точки 1 и 2, разделенные интервалом времени 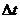 (рис. 1.4), перенесем параллельно самому себе вектор
(рис. 1.4), перенесем параллельно самому себе вектор 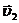 и отложим
и отложим
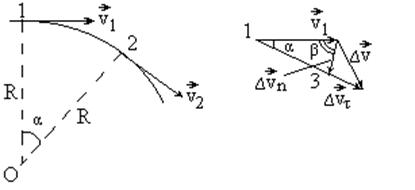
Рис.1.4
на нем отрезок, равный по модулю вектору 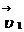 (рис. 1.4, точка 3). Тогда вектор
(рис. 1.4, точка 3). Тогда вектор 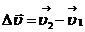 можно представить в виде суммы двух векторов
можно представить в виде суммы двух векторов 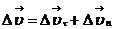 . При
. При 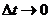 углы α и β стремятся соответственно к 00 и 900, поэтому вектор
углы α и β стремятся соответственно к 00 и 900, поэтому вектор 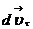 будет направлен по касательной к траектории и будет характеризовать изменение числового значения скорости, а вектор
будет направлен по касательной к траектории и будет характеризовать изменение числового значения скорости, а вектор  будет перпендикулярен к
будет перпендикулярен к 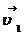 . Следовательно,
. Следовательно,
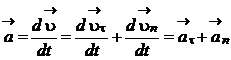 ;
;
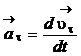 ,
, 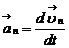 . (1.8)
. (1.8)
Длина дуги и расстояние по прямой между точками 1 и 2 при малых 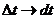 будут равны
будут равны 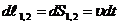 . Из подобия треугольников
. Из подобия треугольников 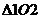 и
и 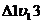 следует
следует
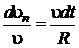 ,
, 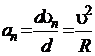 ,
,
что и было записано в формуле (1.6).
*1.1.3. Схема решения основной задачи кинематики.
Формулы для радиус-вектора 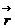 и вектора скорости
и вектора скорости 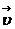
Основной задачей кинематики является определение состояния м.т. (ее радиус-вектора 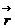 и скорости
и скорости  ) в произвольный момент времени t. Для этого необходимо, задать, во-первых, начальные условия – радиус-вектор
) в произвольный момент времени t. Для этого необходимо, задать, во-первых, начальные условия – радиус-вектор 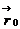 и скорость
и скорость 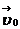 в начальный момент времени t = t0 и, во-вторых, зависимость ускорения
в начальный момент времени t = t0 и, во-вторых, зависимость ускорения 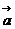 от времени t. Тогда, используя понятие интеграла (см. приложение 1), для
от времени t. Тогда, используя понятие интеграла (см. приложение 1), для 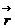 и
и 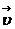 можно записать следующие выражения
можно записать следующие выражения
|
|
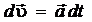 ,
, 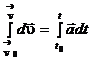 ;
;
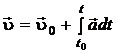 (1.9)
(1.9)
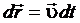 ,
, 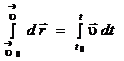 ;
;
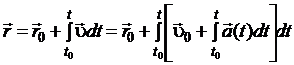 . (1.10)
. (1.10)
Рассмотрим конкретный вид уравнений (1.9), (1.10) для некоторых частных случаев движений м.т.
1. Равнопеременное движение м.т. – это движение м.т. с постоянным ускорением (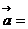 const). При выборе начального момента времени t0 равным нулю, из выражений (1.9) и (1.10) получим
const). При выборе начального момента времени t0 равным нулю, из выражений (1.9) и (1.10) получим
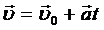 ,
,  . (1.11)
. (1.11)
Формула (1.11) позволяет, например, описать движение брошенного под углом к горизонту тела без учета сил сопротивления воздуха (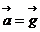 ), движение по параболической траектории.
), движение по параболической траектории.
Равнопеременное прямолинейное движение ( ) будет наблюдаться в тех случаях, когда векторы ускорения
) будет наблюдаться в тех случаях, когда векторы ускорения 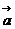 и начальной скорости
и начальной скорости 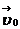 будут либо параллельны друг к другу, либо направлены в противоположные стороны, либо вектор
будут либо параллельны друг к другу, либо направлены в противоположные стороны, либо вектор 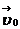 будет равен нулю:
будет равен нулю:  . В этих случаях проекция уравнений (1.11) на ось Oх, направленную вдоль линии движения тела, приводит к следующим выражениям:
. В этих случаях проекция уравнений (1.11) на ось Oх, направленную вдоль линии движения тела, приводит к следующим выражениям:
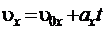 ,
,  . (1.12)
. (1.12)
Для пути  и модуля скорости
и модуля скорости 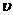 в случаях равноускоренного (знак “+”) и равнозамедленного (знак “-”) прямолинейных движений можно получить
в случаях равноускоренного (знак “+”) и равнозамедленного (знак “-”) прямолинейных движений можно получить
 ,
, 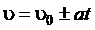 . (1.13)
. (1.13)
На рис.1.5 приведены построенные по уравнениям (1.12) графики зависимости от времени t проекций на ось Oх скорости 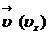 , перемещения
, перемещения  и радиус-вектора
и радиус-вектора 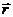 (координата х) при заданных начальных значениях
(координата х) при заданных начальных значениях  ,
,  и зависимости
и зависимости 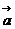 (считается, что
(считается, что 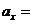 const>0). Этот случай соответствует равноускоренному движению вдоль оси Oх.
const>0). Этот случай соответствует равноускоренному движению вдоль оси Oх.
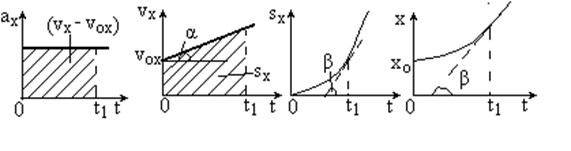
Рис.1.5
Как видно из рис. 1.5, площади под графиком 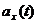 и
и 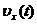 позволяют найти в определенный момент времени t1 значения (
позволяют найти в определенный момент времени t1 значения (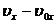 ) и
) и 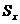 , а углы наклона α и β касательной к графикам
, а углы наклона α и β касательной к графикам  и
и 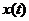 определяют проекцию ускорения ax= tgα и скорости υx= tgβ в этот момент времени t1.
определяют проекцию ускорения ax= tgα и скорости υx= tgβ в этот момент времени t1.
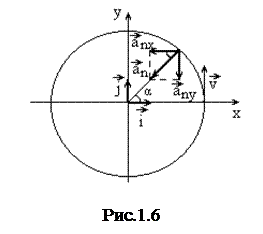 2. Равномерное движение м.т. по окружности радиуса R в плоскости хОу (начало координатных осей находится в центре окружности, рис.1.6). Задаем начальные условия при t = 0:
2. Равномерное движение м.т. по окружности радиуса R в плоскости хОу (начало координатных осей находится в центре окружности, рис.1.6). Задаем начальные условия при t = 0: 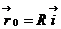 ,
, 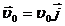
Для такого движения тангенциальное ускорение 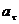 равно нулю, а зависимость нормального ускорения
равно нулю, а зависимость нормального ускорения  от времени t определяется формулой
от времени t определяется формулой
 ,
, 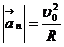 . (1.14)
. (1.14)
Действительно, для положения м.т., соответствующей углу α на рис.1.6, можно записать формулу для  через проекции на оси х и у
через проекции на оси х и у
|
|
 ,
,
причем
 ,
, 
Длина дуги, ограниченная углом α, равна l =α R = v0t, где t - время, за которое м.т. поворачивается на угол α. Тогда α = (υ0t)/R и в итоге получается
формула (1.14).
Подставляя начальные условия и выражения для  в формулы (1.9) и (1.10), получим
в формулы (1.9) и (1.10), получим
 ,
, 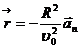 . (1.15)
. (1.15)
Формулы (1.9) и (1.10) даже в простом случае равномерного вращения м.т. по окружности дают громоздкие выражения (1.15). Существенное упрощение описания вращательного движения м.т. возможно при введении новых характеристик – векторов углового перемещения 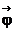 , угловой скорости
, угловой скорости  и углового ускорения
и углового ускорения 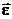 .
.
1.1.4. Кинематические характеристики вращательного движения м.т. и а.т.т.
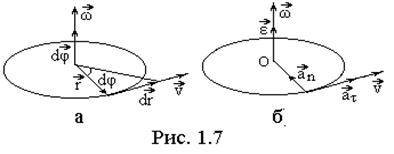 |
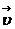 по окружности радиуса r вокруг неподвижной оси вращения (рис. 1.7,а). Материальную точку с осью вращения
по окружности радиуса r вокруг неподвижной оси вращения (рис. 1.7,а). Материальную точку с осью вращения
соединяет перпендикулярный к ней вектор 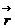 , а вектор его элементарного приращения, вектор
, а вектор его элементарного приращения, вектор 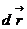 , направлен по касательной к окружности.
, направлен по касательной к окружности.
Введем понятие вектора элементарного углового перемещения  :
:
он равен по модулю углу элементарного поворота d φ, причем d φ>0; направлен вектор  по оси вращения и связан с направлением вращения правилом правого буравчика, а именно, направление вращения буравчика должно совпадать с направлением вращения м.т., тогда поступательное движение буравчика определяет направление вектора
по оси вращения и связан с направлением вращения правилом правого буравчика, а именно, направление вращения буравчика должно совпадать с направлением вращения м.т., тогда поступательное движение буравчика определяет направление вектора  (рис.1.7,а).
(рис.1.7,а).
Быстроту вращения м.т. характеризует угловая скорость  , равная первой производной от вектора углового перемещения
, равная первой производной от вектора углового перемещения 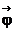 по времени t
по времени t
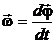 . (1.16)
. (1.16)
Направления вектора угловой скорости  и вектора элементарного углового перемещения
и вектора элементарного углового перемещения  совпадают.
совпадают.
Быстроту изменения угловой скорости характеризует вектор углового ускорения  , равный первой производной от угловой скорости
, равный первой производной от угловой скорости  по времени t
по времени t
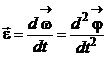 . (1.17)
. (1.17)
В случае ускоренного вращения направления 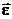 и
и  совпадают (рис.1.7,б), для замедленного вращения вектора
совпадают (рис.1.7,б), для замедленного вращения вектора 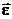 и
и  направлены в противоположные стороны (
направлены в противоположные стороны ( ).
).
Кроме приведенных выше величин, для описания вращательного движения тела используют частоту обращения n, определяемую как число оборотов, совершаемых телом за единицу времени, и период обращения Т как время одного полного оборота. Справедливы следующие формулы взаимосвязи ω, n и Т:
|
|
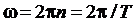 . (1.18)
. (1.18)
Введенные характеристики вращательного движения м.т. применимы и для абсолютно твердого тела, так как его можно разбить на малые объемы и тем самым представить в виде совокупности м.т.
Если задать начальные условия (t =t0: 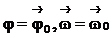 ) и зависимость углового ускорения
) и зависимость углового ускорения 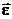 от времени t, то тогда для векторов углового перемещения
от времени t, то тогда для векторов углового перемещения 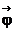 и угловой скорости
и угловой скорости 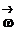 можно записать
можно записать
 ,
, 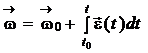 (1.19)
(1.19)
Для вращения тела с постоянным угловым ускорением формула (1.19) примет следующий вид (t0 = 0):
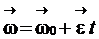 ,
, 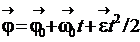 . (1.20)
. (1.20)
Для углового пути φ и модуля угловой скорости ω в случаях равноускоренного (знак “+”) и в случае равнозамедленного (знак “-”) вращения из (1.20) получаем (φ0=0)
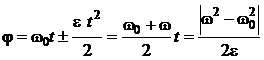 ,
,  (1.21)
(1.21)
Можно отметить, что формулы (1.21) переходят в формулы (1.13) при следующей замене φ → l, ω → υ, ε → a=aτ. Этой аналогией можно пользоваться при записи формул для вращательного движения тел.
1.1.5. Формулы взаимосвязи линейных (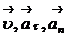 ) и угловых (
) и угловых (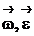 )
)
Законы Ньютона
В основе классической механики движения м.т. лежат три закона Ньютона, они не доказываются, они являются обобщением опытных фактов.
Первый закон Ньютона отвечает на вопрос: как движется тело в отсутствие его взаимодействия с другими телами? Ответ на этот вопрос не является очевидным, так как практически устранить взаимодействие тел невозможно (например, устранить силу трения). Поэтому до Галилея из опыта делался неправильный вывод: равномерное движение тела возможно только при воздействии на тело других тел. Например, если силу трения не устранить, то тело будет двигаться по горизонтальному столу с постоянной скоростью только при наличии внешней силы. Правильный вывод содержится в первом законе Ньютона, согласно которому тело покоится или движется равномерно и прямолинейно, если на него не действуют другие тела или их действие скомпенсировано.
Оказывается, что первый закон Ньютона выполняется не во всех системах отсчета. Если выбрать С.О., связанную с поездом, движущимся равномерно и прямолинейно, то шарик, лежащий на гладком горизонтальном столе в купе вагона, будет покоиться, т.к. действующие на него силы тяжести и нормальной реакции опоры компенсируют друг друга. Однако, если поезд будет двигаться с ускорением, то без видимых причин шарик начнет двигаться относительно поезда, т.е. приобретет ускорение. Поэтому среди всех С.О. выделяют инерциальные системы отсчета (ИСО) как С.О., в которых выполняется первый закон Ньютона и соответственно второй и третий законы Ньютона.
ИСО в природе не существует, так как тела отсчета либо вращаются (С.О., связанная с Землей), либо движутся прямолинейно с ускорением. Наиболее близкой к ИСО можно считать систему отсчета, связанную с Солнцем. Для многих физических явлений систему отсчета, связанную с Землей, также можно считать ИСО. В теоретическом плане ИСО существует бесконечное множество, все они движутся равномерно и прямолинейно, т.е. без ускорения, или покоятся.
|
|
Ньютон для формулировки второго закона ввел понятие импульса  тела как векторную физическую величину, характеризующую его прямолинейное движение и равную произведению массы тела на его скорость
тела как векторную физическую величину, характеризующую его прямолинейное движение и равную произведению массы тела на его скорость
 . (1.26)
. (1.26)
Второй закон Ньютона количественно описывает механическое взаимодействие тел, связывая между собой действующую на тело силу с изменением его импульса. Согласно этому закону первая производная от импульса  тела по времени t равна векторной сумме сил, действующих на тело,
тела по времени t равна векторной сумме сил, действующих на тело,
 . (1.27)
. (1.27)
Формула (1.27) позволяет рассматривать движение, при котором масса тела может изменяться (реактивное движение).
Если масса тела не зависит от времени, то тогда выражение (1.27) можно записать, вводя в него ускорение тела
 (1.28)
(1.28)
и сформулировать второй закон Ньютона следующим образом: произведение массы тела на его ускорение равно векторной сумме сил, действующих на тело.
Можно отметить, что выражение (1.27) приводит в специальной теории относительности к релятивистски инвариантной формуле второго закона Ньютона, чего нельзя сказать о формуле (1.28). В релятивистской механике формула взаимосвязи между ускорением тела и действующей на него силой существенно усложняется.
Уравнение (1.27) и (1.28) позволяют при задании начальных условий (задания радиус-вектора 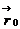 и импульса
и импульса  тела при t = t0) и сил, действующих на тело, решить основную задачу механики м.т., т.е. описать ее механическое движение - однозначно определить состояние м.т. (ее радиус-вектор
тела при t = t0) и сил, действующих на тело, решить основную задачу механики м.т., т.е. описать ее механическое движение - однозначно определить состояние м.т. (ее радиус-вектор 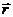 и импульс
и импульс  ) в последующие моменты t. Схема решения задач приведена на рис. 1.9.
) в последующие моменты t. Схема решения задач приведена на рис. 1.9.

Рис.1.9
Третий закон Ньютона важен тем, что он устанавливает дополнительные связи между силами, возникающими при взаимодействии тел, и тем самым облегчает решение уравнений (1.27) и (1.28), т.е. решение задачи о механическом движении тел.
Согласно этому закону силы, действующие между двумя телами, равны по модулю и противоположны по направлению
 . (1.29)
. (1.29)
На рис 1.10 приведены примеры сил, входящих в третий закон Ньютона. Эти силы приложены к разным телам, они одинаковой природы, это силы действия и противодействия.

Рис.1.10
В заключение этого параграфа отметим, что, хотя задача описания механического движения тел решается на основе уравнений (1.27) и (1.28), ее практическая реализация сопряжена с большими сложностями. Так, в частности, во многих случаях не удается установить все силы, действующие на тело, а для известных сил установить их зависимость от координат и времени. К тому же задача о движении трех и более тел не имеет точного решения.
В связи с этим вводят дополнительные величины, такие как импульс  , энергия W и момент импульса
, энергия W и момент импульса  тела. Оказывается, что для этих величин выполняются законы сохранения, которые позволяют, не решая уравнения второго закона Ньютона, получить неполную, но важную для практических целей информацию о движении взаимодействующих тел.
тела. Оказывается, что для этих величин выполняются законы сохранения, которые позволяют, не решая уравнения второго закона Ньютона, получить неполную, но важную для практических целей информацию о движении взаимодействующих тел.
К тому же эти законы сохранения являются отражением установленных на опыте фундаментальных свойств пространства и времени как форм существования материи – однородности пространства (все точки пространства эквивалентны, равноправны; из чего следует закон сохранения импульса) и его изотропности (все направления в пространстве эквивалентны, равноправны, из чего вытекает закон сохранения момента импульса) и однородности времени (все моменты времени равноправны, что приводит к закону сохранения механической энергии).
Возможно и другое, принятое в теоретической физике построение классической механики, в котором постулируются законы сохранения импульса, энергии и момента импульса и на их основе выводятся законы Ньютона. Но это не меняет сути дела, так как и в том, и в другом случае в основе механики лежат законы, являющиеся следствием опытных фактов.
Закон сохранения импульса
Докажем закон сохранения импульса. Для этого рассмотрим систему, состоящую из N тел (на рис.1.11 для простоты приведена система из трех тел - м.т).
На каждое тело системы действуют внешние силы  (
( ) со стороны не входящих в эту систему тел (м.т.), и внутренние силы
) со стороны не входящих в эту систему тел (м.т.), и внутренние силы  (
( ) со стороны других тел системы. Внутренние силы системы связаны между собой третьим законом Ньютона
) со стороны других тел системы. Внутренние силы системы связаны между собой третьим законом Ньютона
 . (1.30)
. (1.30)
Запишем уравнения второго закона Ньютона (1.27) для всех тел системы и затем сложим эти уравнения
 ,
,  ;
;
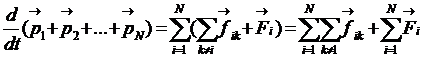 .
.

Рис.1.11
Векторная сумма всех внутренних сил с учетом (1.30) равна нулю и поэтому
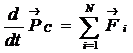 , (1.31)
, (1.31)
где введен импульс 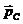 системы как векторная сумма импульсов тел системы
системы как векторная сумма импульсов тел системы
 . (1.32)
. (1.32)
Итак, согласно (1.31) векторная сумма импульсов тел системы (или импульс системы) изменяется за счет действия внешних сил.
Если взять замкнутую систему, т.е. систему, на которую не действуют внешние силы ( ), то тогда выполняется закон сохранения импульса, согласно которому векторная сумма импульсов тел замкнутой системы остается постоянной или импульс
), то тогда выполняется закон сохранения импульса, согласно которому векторная сумма импульсов тел замкнутой системы остается постоянной или импульс 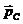 замкнутой системы остается постоянным.
замкнутой системы остается постоянным.
 const,
const,  const. (1.33)
const. (1.33)
Реально выделить замкнутую систему достаточно трудно. Но и в незамкнутых системах в ряде случаев можно использовать закон сохранения импульса. Перечислим их. 1. Внешние силы компенсируют друг друга. Такую систему, например, составляют рассмотренные в §1.2.1 два тела, движущиеся по гладкой горизонтальной поверхности (отсутствуют силы трения) навстречу друг другу (рис.1.8). В этом случае внешние силы – силы тяжести  ,
, 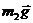 , нормальная реакция опоры
, нормальная реакция опоры  компенсируют друг друга, а возникающие при столкновении тел внутренние силы, силы деформации, не могут изменить импульс системы
компенсируют друг друга, а возникающие при столкновении тел внутренние силы, силы деформации, не могут изменить импульс системы  . Из этого следует, что m1/m2 =
. Из этого следует, что m1/m2 =  , т.е. из закона сохранения импульса можно количественно оценить соотношение масс этих тел, их инертность. 2. Внешние силы не компенсируют друг друга, но их проекция на какую-либо ось остается равной нулю. Хотя импульс системы изменяется, но его проекция на эту ось сохраняется. Примером такой системы является система, состоящая из двух тел, одно из которых движется по гладкой поверхности со скоростью
, т.е. из закона сохранения импульса можно количественно оценить соотношение масс этих тел, их инертность. 2. Внешние силы не компенсируют друг друга, но их проекция на какую-либо ось остается равной нулю. Хотя импульс системы изменяется, но его проекция на эту ось сохраняется. Примером такой системы является система, состоящая из двух тел, одно из которых движется по гладкой поверхности со скоростью  , а другое падает вертикально вниз со скоростью
, а другое падает вертикально вниз со скоростью 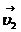 и испытывает абсолютно неупругое столкновение с первым телом. В результате этого они движутся с одинаковой скоростью
и испытывает абсолютно неупругое столкновение с первым телом. В результате этого они движутся с одинаковой скоростью  , образуя единое целое (рис.1.12).
, образуя единое целое (рис.1.12).

Рис.1.12
Сумма внешних сил до удара ( ), во время удара и после удара (
), во время удара и после удара (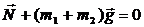 ) изменяется, но их проекция на ось Ох остается все время равной нулю и поэтому
) изменяется, но их проекция на ось Ох остается все время равной нулю и поэтому  . Такие системы называются квазизамкнутыми. 3. Внешние силы значительно меньше по модулю внутренних сил, действующих между телами в системе (
. Такие системы называются квазизамкнутыми. 3. Внешние силы значительно меньше по модулю внутренних сил, действующих между телами в системе ( ). Это наблюдается при сильных кратковременных взаимодействиях: удар, выстрел, разрыв снаряда и т.д. В этих случаях изменение импульса каждого тела системы, в основном, определяется внутренними силами системы
). Это наблюдается при сильных кратковременных взаимодействиях: удар, выстрел, разрыв снаряда и т.д. В этих случаях изменение импульса каждого тела системы, в основном, определяется внутренними силами системы
 . (1.34)
. (1.34)
1.2.4. Центр масс системы. Центр масс и центр тяжести а.т.т.
Под центром масс системы понимают точку пространства, положение которой относительно какой-либо ИСО определяется радиус-вектором 
 ,
, 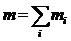 , (1.35)
, (1.35)
где m – сумма масс тел (материальных точек) системы;  - радиус-вектор
- радиус-вектор  – го тела (м.т.) системы.
– го тела (м.т.) системы.
Если поместить в центр масс тело в виде материальной точки массы m, то оно будет двигаться со скоростью  , равной
, равной
 . (1.36)
. (1.36)
Если подставить в выражение (1.36) формулу (1.31)
 , (1.37)
, (1.37)
то тогда можно сказать, что центр масс системы - это точка пространства, к которой приложены все силы, вызывающие по отдельности поступательное движение системы. Поэтому поступательное движение системы можно моделировать движением тела в виде м.т. массы m, помещенного в центре масс системы. Этот прием является удобным при изучении такого движения системы.
Если система является замкнутой или внешние силы, действующие на нее, компенсируют друг друга, то ее центр масс будет двигаться равномерно и прямолинейно или покоиться. Поэтому в ИСО, связанной с ним, проще описать движение тел системы.
В качестве примера рассмотрим систему двух неподвижных тел массами m1 и m2 (m2= 2m1), скрепленных между собой сжатой в начальный момент времени пружиной. Эти тела могут скользить без трения по гладкой горизонтальной поверхности (рис.1.13)

Рис.1.13
Начало оси 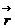 , точка О, совпадает с центром масс системы (точкой С), т.е.
, точка О, совпадает с центром масс системы (точкой С), т.е.  . Положение тел в начальный момент времени определится векторами
. Положение тел в начальный момент времени определится векторами  и
и  , связанными между собой соотношением
, связанными между собой соотношением
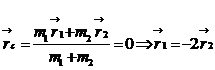 .
.
Если пружину отпустить, то за счет действия внутренних сил системы (силы упругости) тела приходят в движение, скорости  и
и 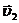 , радиус-векторы
, радиус-векторы  и
и  будут все время изменяться, но положения центра масс остается при этом неизменным, а импульс системы будет равным нулю
будут все время изменяться, но положения центра масс остается при этом неизменным, а импульс системы будет равным нулю
 .
.
Соотношения между радиус-векторами  (
( ) и векторами
) и векторами  и
и  сохраняются при движении тел.
сохраняются при движении тел.
Введенное выше понятие центра масс системы включает в себя как частный случай понятия центра масс и для абсолютно твердого тела. Действительно а.т.т. можно разбить на малые объемы dV и представить в виде совокупности м.т., между которыми действуют внутренние силы. Отличием для а.т.т. является тот факт, что расстояния между м.т. этого тела остаются со временем неизменными. Размеры объемов dV (м.т.) нужно выбирать такими, чтобы можно было пренебречь дискретным (атомным) строением вещества, т.е. эти объемы должны содержать достаточное количество одинаковых по свойствам атомов.
Центр масс а.т.т. совпадает с его центром тяжести, но является более общим понятием, справедливым и в отсутствие внешних гравитационных полей. Положение центра масс а.т.т. можно найти экспериментально, определяя положение его центра тяжести (см. параграф 1.3.3).
Лекция 3
Лекция 4
Лекция 5
Лекция 6
Лекция 7
Кинематика С.Т.О.
Понятие «длина» предмета
Пусть в С.О. К' вдоль оси О 'х' располагается неподвижный стержень, длина которого может быть найдена как разность координат его концов 
(рис.1.29). Необходимо определить длину этого стержня в С.О. К, относительно которой он движется со скоростью u (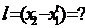 ).
).
Для определения длины l стержня используем преобразования Лоренца и укажем метод определения длины l движущегося стержня: необходимо в С.О. К одновременно зафиксировать координаты концов стержня  , в результате чего можно получить
, в результате чего можно получить

 . (1.92)
. (1.92)
В формуле (1.92) через l0 обозначена собственная длина стержня, это длина стержня в той ИСО, относительно которой он неподвижен (в рассматриваемом случае l0=l'). Собственная длина предмета является инвариантом С.Т.О.
· Из формулы (1.92) следует, что: 1) при движении предметов происходит сокращение продольных, направленных вдоль скорости, размеров предметов; поперечные, перпендикулярные к скорости движения, размеры тел не изменяются; 2) собственная длина предмета l0 является наибольшей из всех возможных длин предмета.
· Итак, понятие «длина» предмета является относительным, т.е. зависит от выбора ИСО. В классической механике u<<c и поэтому понятие «длины предмета» является абсолютным, одинаковым во всех ИСО.
·
· 1.5.4.3. Понятие«промежутоквремени»междудвумя событиями
·
· Пусть в С.О. K' в одной точке пространства ( ) происходят два события или протекает какой-либо процесс. Промежуток времени
) происходят два события или протекает какой-либо процесс. Промежуток времени  в С.О. K ' можно измерить одними часами, находящимися в этой точке пространства. Возникает вопрос, чему равняется этот промежуток времени в С.О. К (Δt=t2-t1), относительно которой эти события происходят в разных точках оси Ох (
в С.О. K ' можно измерить одними часами, находящимися в этой точке пространства. Возникает вопрос, чему равняется этот промежуток времени в С.О. К (Δt=t2-t1), относительно которой эти события происходят в разных точках оси Ох ( ).
).
· Вполне понятно, что промежуток времени ∆t нужно измерять двумя часами, расположенными в разных точках оси Ох - в одной точке (х=х1) находятся часы, измеряющие время одного события (t=t1) или начало процесса, а во второй (х=х2) находятся часы, измеряющие время другого события (t=t1) или окончание процесса.
Для определения ∆t используем преобразования Лоренца
·  ,
,
·  , (1.93)
, (1.93)
где ∆t0 – собственный промежуток времени, он измеряется одними часами в той ИСО, относительно которой события происходят в одной точке пространства, это инвариант С.Т.О.
Из формулы (1.93) следует, что 1) ∆t > ∆t0, т.е. в движущейся ИСО происходит замедление хода времени, движущиеся часы идут медленнее покоящихся; 2) ∆t0 £ ∆t, т.е. собственный промежуток времени между двумя событиями является наименьшим из всех возможных промежутков времени для этих событий.
Замедление хода времени в движущейся системе отсчета подтверждается экспериментами с участием нестабильных элементарных частиц, рождающихся в ядерных реакциях со скоростями, близкими к скорости света в вакууме (например, u = 0,99с). В этом случае время их жизни до распада существенно различается в С.О. К ', связанной с ними (собственное время ∆t0, равное, например, ∆t0 =25 нс), и в С.О. К, связанной с Землей (время жизни  0). Это приводит к тому, что с учетом замедления времени частица пролетает в С.О. К до распада значительно большее расстояние (l=u ∆t =52 м.), чем без учета этого эффекта (l'=u∆t0= 7,4 м).
0). Это приводит к тому, что с учетом замедления времени частица пролетает в С.О. К до распада значительно большее расстояние (l=u ∆t =52 м.), чем без учета этого эффекта (l'=u∆t0= 7,4 м).
Такие частицы регистрируют на расстояниях l от места их рождения, значительно превышающих l’. Отметим, что в С.О. К ', связанной с частицей, расстояние l' проходит Земля мимо неподвижной частицы за время ее жизни ∆t0.
В силу равноправия всех ИСО замедления времени в С.Т.О. носит относительный характер. Наблюдатель, находящийся на Земле, отметит, что движения космонавта в ракете, движущейся со скоростью u, близкой к скорости света, будут замедленными по сравнению с его движениями. То же самое скажет космонавт, наблюдая за человеком на Земле. И они оба будут правы, так как космонавт может считать систему отсчета, связанную с ним, неподвижной, а систему отсчета, связанную с Землей, движущейся со скоростью u в обратном направлении.
Лекция 8
Динамика С.Т.О.
Лекция 9
* 1.6. Описание движения тел в неинерциальных
Системах отсчета (НИСО)
Пусть относительно ИСО под действием сил 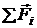 , тело движется с ускорением
, тело движется с ускорением 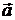
<
|
|
|

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!