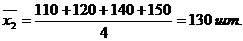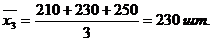При изучении вариации примеряются такие характеристики вариационного ряда, которые описывают количественного его структуру, строение.
Медиана (Ме) – величина варьирующего признака, делящая совокупность на две равные части – со значениями признака меньше медианы и со значениями признака больше медианы. В интервальном вариационном ряду для нахождения медианы применяется следующая формула:
 (5.3)
(5.3)
где Ме – медиана; x0 – нижняя граница интервала, в котором находится медиана; 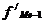 – накопленная частота в интервале, предшествующем медианному;
– накопленная частота в интервале, предшествующем медианному; 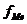 – частота в медианном интервале; i – величина интервала; k – число групп.
– частота в медианном интервале; i – величина интервала; k – число групп.
В дискретном вариационном ряду медианой следует считать значение признака в той группе, в которой накопленная частота превышает половину численности совокупности.
Пример. Найдеммедиану в нашем примере. Для этого составим табл. 5.1.
Таблица 5.1. Распределение предприятий общественного питания области по объему розничного товарооборота
Группы предприятий по розничному товарообороту, млн. руб. ( ) )
| Число предприятий ( ) )
| Середина интервала, млн. руб. ( ) )
| 
| Накопленная частота ( ) )
|
| 100 – 170
170 – 240
240 – 310
310 – 380
380 – 450
450 – 520
520 - 590
|
|
|
|
|
| Итого
|
| –
|
| –
|
В табл. 5.1 медианным является среднее из 65 значений, т.е. тридцать второе от начала ряда значение розничного товарооборота. Как видно из ряда накопленных частот, оно находится в третьем интервале. Тогда:

При нечетном числе единиц совокупности номер медианы, как видно, равен не  , как в формуле (5.3), а
, как в формуле (5.3), а  , но это различие несущественно и обычно игнорируется на практике.
, но это различие несущественно и обычно игнорируется на практике.
Квартили (Q) – значения признака, делящие совокупность на четыре равные по числу единиц части. Для первого и третьего квартилей используются следующие формулы:
 (5.4)
(5.4)
 (5.5)
(5.5)
Второй квартиль, совпадает с медианой.
Пример. Рассчитаем первый и третий квартиль для нашего примера.
 ;
;

Значения признака, делящие ряд на пять равных частей, называют квинтилями, на десять частей – децилями, на сто частей – перцентилями.
Мода (Мо) – наиболее часто встречающееся значение признака в совокупности.
В интервальном вариационном ряду для нахождения моды применяется следующая формула:
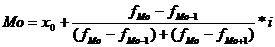 , (5.6)
, (5.6)
где x0 – нижняя граница модального интервала; fМо – частота в модальном интервале; fМо-1 – частота в предыдущем интервале; fМо+1 – частота в следующем интервале за модальным; i – величина интервала.
Пример. По данным табл. 5.1 рассчитаем моду:
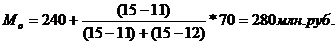
Вычисление моды в интервальном ряду весьма условно.
К изучению структуры вариационного ряда средняя арифметическая величина тоже имеет отношение, хотя основное значение этого обобщающего показателя другое. В ряду распределения хозяйств по урожайности (табл. 5.1) средняя величина урожайности вычисляется как взвешенная по частоте середина интервала x/ по формуле:
 (5.7)
(5.7)

Различие между средней арифметической величиной, медианой и модой невелико. Если распределение по форме близко к нормальному закону, то медиана находится между модой и средней величиной, причем ближе к средней величине, чем к моде.
Показатели вариации
К основным показателям вариации относятся:
1. Размах или амплитуда вариации (R) – абсолютная разность между максимальным и минимальным значениями признака из имеющихся в совокупности значений. Размах вариации вычисляется по формуле:
 (5.8)
(5.8)
Безусловным достоинством этого показателя является простота расчета. Однако размах вариации зависит от величины только крайних значений признака, поэтому область его применения ограничена достаточно однородными совокупностями.
2. Среднее линейное отклонение ( ) по абсолютной величине вычисляется как взвешенное по частоте отклонение по модулю середин интервалов от средней арифметической величины. Среднее линейное отклонение вычисляется по формуле:
) по абсолютной величине вычисляется как взвешенное по частоте отклонение по модулю середин интервалов от средней арифметической величины. Среднее линейное отклонение вычисляется по формуле:
 (5.9)
(5.9)
Простота расчета и интерпретации составляют положительные стороны данного показателя, однако математические свойства модулей «плохие»: их нельзя поставить в соответствие с каким-либо вероятностным законом, в том числе и с нормальным распределением, параметром которого является не средний модуль, а среднее квадратическое отклонение.
Пример. По данным табл. 5.1 рассчитаем среднее линейное отклонение.

Это означает, что в среднем розничный товарооборот в изучаемой совокупности предприятий общественного питания отклонялся от среднего товарооборота по области на 103,2 млн. руб..
3. Дисперсия ( ) – средняя из квадратов отклонений вариантов значений признака от их средней величины. Дисперсия рассчитывается по следующим формулам:
) – средняя из квадратов отклонений вариантов значений признака от их средней величины. Дисперсия рассчитывается по следующим формулам:
а) простая (для несгруппированных данных):
 (5.10)
(5.10)
б) взвешенная (для сгруппированных данных):
 (5.11)
(5.11)
Дисперсия обладает рядом свойств, некоторые из которых позволяют упростить ее вычисления:
§ дисперсия постоянной величины равна нулю;
§ если все варианты значения признака уменьшить на одно и то же число, то дисперсия не уменьшится;
§ если все варианты значений признака уменьшить в одно и то же число раз (k раз), то дисперсия уменьшиться в k2 раз.
4. Среднее квадратическое отклонение ( ) представляет собой корень квадратный из дисперсии. Данный показатель рассчитывается по следующим формулам:
) представляет собой корень квадратный из дисперсии. Данный показатель рассчитывается по следующим формулам:
а) для несгруппированных данных:
 (5.12)
(5.12)
б) для вариационного ряда:
 (5.13)
(5.13)
Среднее квадратическое отклонение по величине в реальных совокупностях всегда больше среднего модуля отклонений. Соотношение  зависит от наличия в совокупностях резких, выделяющихся отклонений и может служить индикатором «засоренности» совокупности неоднородными с основной массой элементами: чем это соотношение больше, тем сильнее подобная «засоренность». Для нормального закона распределения
зависит от наличия в совокупностях резких, выделяющихся отклонений и может служить индикатором «засоренности» совокупности неоднородными с основной массой элементами: чем это соотношение больше, тем сильнее подобная «засоренность». Для нормального закона распределения  .
.
Пример. По данным табл. 5.1 среднее квадратическое отклонение розничного товарооборота предприятий общественного питания составило:
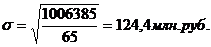
5. Среднее квартильное расстояние. Данный показатель силы вариации, характеризует ее не по всей совокупности, а лиши в центральной части, т.е. средняя величина разности между квартилями. Данный показатель рассчитывается по формуле:
 (5.14)
(5.14)
где q – среднее квартильное расстояние; Q1 и Q3 – соответственно первая и третья квартили распределения.
Этот показатель можно применить вместо размаха вариации, чтобы избежать недостатков, связанных с использованием крайних значений.
6. Для оценки интенсивности вариации и для сравнения ее в разных совокупностях и тем более разных признаков необходимы относительные показатели вариации. Они вычисляются как отношение абсолютных показателей силы вариации, рассмотренных ранее, к средней арифметической величине признака. Получаем следующие показатели:
а) относительный размах вариации 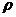 :
:
 (5.15)
(5.15)
б) относительное отклонение по модулю m:
 (5.16)
(5.16)
в) коэффициент вариации как относительное квадратическое отклонение  :
:
 (5.17)
(5.17)
г) относительное квартильное расстояние d:
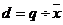 (5.18)
(5.18)
Наиболее часто применяемый показатель относительной колеблемости – коэффициент вариации. Его используют не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному).
7. Межгрупповая дисперсия ( ) является мерой колеблемости частных средних по группам
) является мерой колеблемости частных средних по группам  вокруг общей средней
вокруг общей средней  и исчисляется по формуле:
и исчисляется по формуле:
 (5.19)
(5.19)
где k – число групп; nj – число единиц в j-й группе;  – частная средняя по j-й группе;
– частная средняя по j-й группе;  – общая средняя по совокупности единиц.
– общая средняя по совокупности единиц.
8. Внутригрупповая дисперсия ( ) характеризует вариацию, обусловленную влиянием случайных факторов, и рассчитывается по формуле:
) характеризует вариацию, обусловленную влиянием случайных факторов, и рассчитывается по формуле:
 (5.20)
(5.20)
9. По совокупности в целом вариация значений признака под влиянием прочих факторов характеризуется средней из внутренних дисперсий:
 . (5.21)
. (5.21)
Сумма указанных дисперсий образует общую дисперсию признака:
 . (5.22)
. (5.22)
Данное равенство определяет правило сложения дисперсий. Оно используется, в частности, в корреляционном анализе при определении тесноты связи результативного признака и факторных.
Пример. О производительности станков одного из цехов предприятия известны следующие данные (табл. 5.2). По этим данным необходимо определить:
a. внутригрупповую дисперсию по выработке деталей одним станком, определенного вида;
b. среднюю из внутригрупповых дисперсий по трем группам станков;
c. межгрупповую дисперсию;
d. общую дисперсию производительности станков данного цеха.
Таблица 5.2. Информация о производительности станков одного из цеха
| Вид станков
| Число станков
| Дневная выработка деталей одним станком, шт.
|
| Сверлильные
Фрезерные
Шлифовальные
|
| 150, 200
110, 120, 140, 150
200, 220, 250
|
1. Исчислим вначале средние по каждой группе:

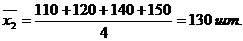
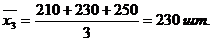
2. Для расчета внутригрупповых дисперсий будем использовать формулу (5.20).



3. Определим среднюю из внутригрупповых дисперсий, используя формулу (5.21):

4. Определим общую среднюю величину для расчета межгрупповой дисперсии:

5. Определим межгрупповую дисперсию, используя формулу (5.19):

6. Вычислим общую дисперсию, используя формулу (5.22):




 (5.3)
(5.3)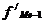 – накопленная частота в интервале, предшествующем медианному;
– накопленная частота в интервале, предшествующем медианному; 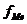 – частота в медианном интервале; i – величина интервала; k – число групп.
– частота в медианном интервале; i – величина интервала; k – число групп. )
)
 )
)
 )
)

 )
)

 , как в формуле (5.3), а
, как в формуле (5.3), а  , но это различие несущественно и обычно игнорируется на практике.
, но это различие несущественно и обычно игнорируется на практике. (5.4)
(5.4) (5.5)
(5.5) ;
;
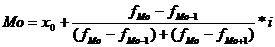 , (5.6)
, (5.6)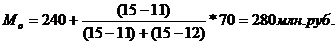
 (5.7)
(5.7)
 (5.8)
(5.8) ) по абсолютной величине вычисляется как взвешенное по частоте отклонение по модулю середин интервалов от средней арифметической величины. Среднее линейное отклонение вычисляется по формуле:
) по абсолютной величине вычисляется как взвешенное по частоте отклонение по модулю середин интервалов от средней арифметической величины. Среднее линейное отклонение вычисляется по формуле: (5.9)
(5.9)
 ) – средняя из квадратов отклонений вариантов значений признака от их средней величины. Дисперсия рассчитывается по следующим формулам:
) – средняя из квадратов отклонений вариантов значений признака от их средней величины. Дисперсия рассчитывается по следующим формулам: (5.10)
(5.10) (5.11)
(5.11) ) представляет собой корень квадратный из дисперсии. Данный показатель рассчитывается по следующим формулам:
) представляет собой корень квадратный из дисперсии. Данный показатель рассчитывается по следующим формулам: (5.12)
(5.12) (5.13)
(5.13) зависит от наличия в совокупностях резких, выделяющихся отклонений и может служить индикатором «засоренности» совокупности неоднородными с основной массой элементами: чем это соотношение больше, тем сильнее подобная «засоренность». Для нормального закона распределения
зависит от наличия в совокупностях резких, выделяющихся отклонений и может служить индикатором «засоренности» совокупности неоднородными с основной массой элементами: чем это соотношение больше, тем сильнее подобная «засоренность». Для нормального закона распределения  .
.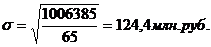
 (5.14)
(5.14)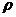 :
: (5.15)
(5.15) (5.16)
(5.16) :
: (5.17)
(5.17)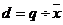 (5.18)
(5.18) ) является мерой колеблемости частных средних по группам
) является мерой колеблемости частных средних по группам  вокруг общей средней
вокруг общей средней  и исчисляется по формуле:
и исчисляется по формуле: (5.19)
(5.19) ) характеризует вариацию, обусловленную влиянием случайных факторов, и рассчитывается по формуле:
) характеризует вариацию, обусловленную влиянием случайных факторов, и рассчитывается по формуле: (5.20)
(5.20) . (5.21)
. (5.21) . (5.22)
. (5.22)