

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
Топ:
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении...
Интересное:
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
идеальной жидкости и их интегрирование (уравнений Эйлера).
В потоке идеальной жидкости возьмем произвольную точку М с координатами x, y, z (рис.5.6) и выделим вблизи этой точки малый объем в форме прямоугольного параллелепипеда так, чтобы точка М была одной из его вершин. Пусть ребра этого параллелепипеда будут параллельны координатным осям и соответственно равны δх, δу и δz, тогда его объем равен δW = δх*δу*δz, а масса δМ= ρδхδуδz.

Составим уравнение движения этого объема. Действующая на объем результирующая массовая сила, может быть разложена на составляющие соответственно осям координат, и, будучи отнесена к массе объема, даст единичные массовые силы или проекции ускорений на оси: Х, У и Z.
Проекции массовых сил, действующих на выделенный объем, равны этим составляющим, умноженным на массу выделенного объема.
Если давление в точке М обозначить через Р, давление вдоль оси Х в точке N - 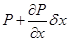 будет сумой давления в точке М и приращения по координате Х.
будет сумой давления в точке М и приращения по координате Х.
Разность между значениями давлений в этих точках, умноженная на площадь даст нам силу, действующую вдоль оси Х
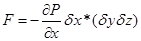 .
.
Принцип Д’Аламбера: При движении системы ее положение может рассматриваться, как положение равновесия, если к активным силам, действующим на систему, прибавить фиктивные силы(силы инерции).
Скорость движения жидкости в точке М обозначим через V, а ее проекции через Vх, VyVz. Проекции ускорения, с которыми движется выделенный объем, будут равны: Vх/dt, Vy/dt, Vz/dt.
По принципу Д’Аламбера силы, которые необходимо ввести в уравнения движения, равны произведению ускорений на массу параллелепипеда.
Уравнения движения выделенного объема жидкости в проекциях на координатные оси будут иметь вид
|
|
ρ*δхδyδz*(dVх/dt) = Xρδхδyδz - (dp/dx)* δхδyδz;
{ ρ*δхδyδz*(dVy/dt) = Yρδхδyδz - (dp/dy)* δхδyδz;
ρ*δхδyδz*(dVz/dt) = Zρδхδyδz - (dp/dz)* δхδyδz;
где X,Y, Z – проекции единичных массовых сил.
Разделим эти уравнения почленно на массу элемента δm = ρ * δхδyδz и перейдем к пределу, устремляя одновременно δх, δy и δz к нулю и, стягивая параллелепипед к точке М, получим уравнения движения жидкости. Это система дифференциальных уравнений движения идеальной жидкости, называемая уравнениями Эйлера.
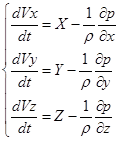 (5.16)
(5.16)
Члены этих уравнений представляют собой соответствующие ускорения, а смысл каждого из уравнений заключается в следующем: полное ускорение частицы вдоль координатной оси складывается из ускорения от массовых сил и ускорения от сил давления.
Уравнения Эйлера в таком виде справедливы как для несжимаемой, так и для сжимаемой жидкости, а также для случая, когда из массовых сил действует только сила тяжести, и для общего случая относительного движения жидкости. При этом в величины Х, У и Z входят компоненты ускорения переносного движения. Так как при выводе уравнений (5.16) не накладывались условия стационарности движения, то они справедливы и для неустановившегося движения.
Рассматривая установившееся движение жидкости, умножим каждое из уравнений (5.16) на проекции элементарного перемещения по осям и сложим уравнения:

В проекциях на ось X: 
В проекциях на ось Y: 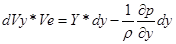
В проекциях на ось Z: 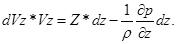
Просуммировав эти проекции, получим:
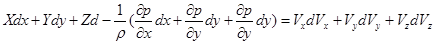 (5.17)
(5.17)
Учитывая, что выражение в скобках является полным дифференциалом давления: 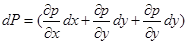 .
.
Произведение проекции скорости на дифференциал скорости можно выразить следующим образом:

Уравнение (5.17) можно переписать в следующем виде
Xdx +Ydy + Zdz = (1/ρ) *(dp) + d(V2/2), (5.18)
или dU = (1/ρ) *(dp) + d(V2/2).
где U – силовая функция.
Интегрирование этого уравнения выполним для основного частного случая установившегося движения идеальной жидкости, когда на жидкость действует лишь одна массовая сила - сила тяжести. При направлении оси вертикально вверх
|
|
X = 0, Y= 0, Z = - g.
Подставляя эти значения в уравнение (5.17) получим
gdz + dp/ρ + d(V2/2) = 0 или dz + dp/(gρ) + d(V2/2g) = 0.
Так как для несжимаемой жидкости ρ = const, предыдущее уравнение можно переписать в виде
d(z + p/(gρ) + (v2/2g)) = 0
Это уравнение означает, что приращение суммы трех членов, заключенных в скобки, при перемещении частицы жидкости вдоль линии тока (траектории) равно нулю, следовательно, указанный трехчлен есть величина постоянная вдоль линии тока, а следовательно, и вдоль элементарной струйки, т. е.
z + p/(gρ) + (v2/2g) → const.
Таким образом, получили уравнение Бернулли для струйки идеальной жидкости, найденное в предыдущем параграфе другим способом.
Если записать это уравнение для двух сечений струйки 1-1 и 2-2, оно примет вид первой формы уравнения Бернулли:
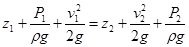 = Н
= Н
|
|
|

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!