1) Определим скорость истечения жидкости из маленького отверстия в большом сосуде с жидкостью. Пусть h – высота верхнего уровня жидкости по отношению к положению отверстия. Давление над жидкостью и около отверстия равно атмосферному, то есть внешнее давление одинаково везде ( ). В очень большом сосуде при истечении жидкости из маленького отверстия скорость жидкости можно считать равной нулю (
). В очень большом сосуде при истечении жидкости из маленького отверстия скорость жидкости можно считать равной нулю ( ). Следовательно, в верхней точки жидкости (где высота – h, а
). Следовательно, в верхней точки жидкости (где высота – h, а  ), то есть в левой части уравнения Бернулли, получаем величину
), то есть в левой части уравнения Бернулли, получаем величину  .
.
В нижней части около отверстия на глубине h (где  , а
, а  ), то есть в правой части уравнения Бернулли, получаем величину
), то есть в правой части уравнения Бернулли, получаем величину  .
.

Из этого равенства легко найти скорость (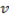 ) истечения жидкости из маленького отверстия:
) истечения жидкости из маленького отверстия:  .
.
2) Измерим давление жидкости с помощью манометра (прибор, который имеет небольшую площадь поверхности, располагается в трубке тока определённым образом). Расположим манометр так, чтобы его поверхность была параллельна линиям тока. При этом манометр будет показывать давление в жидкости, которая течёт со скоростью v (манометр, расположенный параллельно линиям тока, не будет влиять на эту линию), следовательно, в левой части уравнения Бернулли получаем величину  .
.
Расположим манометр перпендикулярно линиям тока. Такое положение манометра влияет на течение жидкости. Жидкость у поверхности манометра будет останавливаться (обтекать манометр). То есть скорость в точке у поверхности манометра будет равна 0 ( ), поэтому в правой части уравнения Бернулли получаем величину
), поэтому в правой части уравнения Бернулли получаем величину  .
.
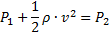
Такое соотношение используется для определения скорости течения жидкости.
Домашнее задание
1. Что такое линия тока?
2. Упражнение 16 (21, 24), стр. 478. Учебник: «Физика. Механика. 10 кл.» (см. список рекомендованной литературы)
3. Струя жидкости со скоростью  бьет в неподвижную стену перпендикулярно ее поверхности. Найдите давление, которое производит жидкость на стену в точке, находящейся на оси струи. Атмосферное давление
бьет в неподвижную стену перпендикулярно ее поверхности. Найдите давление, которое производит жидкость на стену в точке, находящейся на оси струи. Атмосферное давление  , плотность жидкости
, плотность жидкости 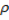 .
.
Список рекомендованной литературы
1. М.М. Балашов, А.И. Гомонова, А.Б. Долицкий и др.; Под ред. Г.Я. Мякишева. Физика. Механика. 10 кл. Профильный уровень. – М.: Дрофа, 2004.
2. Парфентьева Н., Фомина М. Решение задач по физике: Часть 1. – М.: Мир, 1993.
3. А.В. Пёрышкин, В.В. Крауклис. Курс физики т. 1. – М.: Гос. уч.-пед. изд. мин. просвещения РСФСР, 1957.
Уравнение неразрывности. Уравнение Бернулли
Уравнение неразрывности.
Идеальная жидкость - это абстрактная жидкость, не обладающая вязкостью, теплопроводностью, способностью к электризации и намагничиванию.
Такое приближение допустимо для маловязкой жидкости. Течение жидкости называется стационарным, если вектор скорости в каждой точке пространства остается постоянным.
Графически движение жидкостей изображается с помощью линий тока.
 Линии тока жидкости - это линии, в каждой точке которых вектор скорости частиц жидкости направлен по касательной (рис. 4).
Линии тока жидкости - это линии, в каждой точке которых вектор скорости частиц жидкости направлен по касательной (рис. 4).
Линии тока проводят так, чтобы число линий, проведенных через некоторую единичную площадку, ^ потоку, было численно равно или пропорционально скорости жидкости в данном месте.
Часть жидкости, ограниченная линиями тока, называется трубкой тока.
Т.к. скорость частиц жидкости направлена по касательной к стенкам трубки тока, частицы жидкости не выходят из трубки тока, т.е. трубка - как жесткая конструкция. Трубки тока могут сужаться или расширяться в зависимости от скорости жидкости, хотя масса жидкости, протекающей через некоторое сечение, ^ ее течению, за определенный промежуток времени будет постоянной.
 Т.к. жидкость несжимаема, через S1 и S2 пройдет за Dt одинаковая масса жидкости (рис. 5).
Т.к. жидкость несжимаема, через S1 и S2 пройдет за Dt одинаковая масса жидкости (рис. 5).

 - уравнение неразрывности струи или теорема Эйлера.
- уравнение неразрывности струи или теорема Эйлера.
Произведение скорости течения несжимаемой жидкости и площади поперечного сечения одной и той же трубки тока постоянно.
 Теорема о неразрывности широко применяется при расчетах, связанных с подачей жидкого топлива в двигатели по трубам переменного сечения. Зависимость скорости потока от сечения канала, по которому течет жидкость или газ, используется при конструировании сопла ракетного двигателя. В месте сужения сопла (рис. 6) скорость истекающих из ракеты продуктов сгорания резко возрастает, а давление падает, благодаря чему возникает дополнительная сила тяги.
Теорема о неразрывности широко применяется при расчетах, связанных с подачей жидкого топлива в двигатели по трубам переменного сечения. Зависимость скорости потока от сечения канала, по которому течет жидкость или газ, используется при конструировании сопла ракетного двигателя. В месте сужения сопла (рис. 6) скорость истекающих из ракеты продуктов сгорания резко возрастает, а давление падает, благодаря чему возникает дополнительная сила тяги.
Уравнение Бернулли.
 Пусть жидкость движется в поле сил тяжести так, что в данной точке пространства величина и направление скорости жидкости остаются постоянными. Такое течение называется стационарным. В стационарно текущей жидкости кроме сил тяжести действуют еще и силы давления. Выделим в стационарном потоке участок трубки тока, ограниченный сечениями S1 и S2 (рис.7)
Пусть жидкость движется в поле сил тяжести так, что в данной точке пространства величина и направление скорости жидкости остаются постоянными. Такое течение называется стационарным. В стационарно текущей жидкости кроме сил тяжести действуют еще и силы давления. Выделим в стационарном потоке участок трубки тока, ограниченный сечениями S1 и S2 (рис.7)
За время Dt этот объем переместится вдоль трубки тока, причем сечение S1 переместится в положение 1', пройдя путь  , а S2 - в положение 2', пройдя путь
, а S2 - в положение 2', пройдя путь  . В силу неразрывности струи выделенные объемы (и их массы) одинаковы:
. В силу неразрывности струи выделенные объемы (и их массы) одинаковы:
 ,
,  .
.
Энергия каждой частицы жидкости слагается из ее кинетической и потенциальной энергий в поле сил земного тяготения. Вследствие стационарности течения частица, находящаяся через Dt в любой из точек незаштрихованной части рассматриваемого объема, имеет такую же скорость, и, следовательно Wк, какую имела частица, находившаяся в той же точке в начальный момент времени. Поэтому изменение энергии всего рассматриваемого объема можно вычислить как разность энергий заштрихованных объемов V1 и V2.
Возьмем сечение трубки тока и отрезки  настолько малыми, чтобы всем точкам каждого из заштрихованных объемов можно было приписать одно и то же значение скорости, давления и высоты. Тогда приращение энергии равно:
настолько малыми, чтобы всем точкам каждого из заштрихованных объемов можно было приписать одно и то же значение скорости, давления и высоты. Тогда приращение энергии равно:

В идеальной жидкости трение отсутствует, поэтому DW должно равняться работе, совершенной над выделенным объемом силами давления:
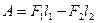
(«-» т.к.  направлена в сторону, противоположную перемещению
направлена в сторону, противоположную перемещению  )
)
 ,
,  ,
,
 ,
,
 ,
,
 .
.
Сократим на V и перегруппируем члены:
 ,
,
сечения S1 и S2 были выбраны произвольно, поэтому можно утверждать, что в любом сечении трубки тока
 (1)
(1)
Выражение (1) представляет собой уравнение Бернулли. В стационарно текущей идеальной жидкости вдоль любой линии тока выполняется условие (1).
Для горизонтальной линии тока  ,
, 
Уравнение Бернулли достаточно хорошо выполняется для реальных жидкостей, внутреннее трение в которых не очень велико.
Уменьшение давления в точках, где скорость потока больше, положено в основу устройства водоструйного насоса.
Выводы этого уравнения учитываются при расчетах конструкций насосов систем подачи жидкого топлива в двигатели.
Движение жидкости. Уравнение Бернулли
Чтобы описать движение жидкости, можно поступить двумя способами. Можно проследить за движением каждой индивидуальной частицы жидкости, то есть указать ее положение и скорость в каждый момент времени. То есть мы будем знать траектории всех частиц. Но можно поступить иначе. Можно проследить, что происходит с течением времени в каждой точке пространства. То есть, можно указать величины и направления скоростей различных частиц жидкости, которые в различные моменты времени проходят через одну и ту же точку пространства. Если рассматривать все возможные точки пространства в какой-то фиксированный момент времени, то при втором способе описания мы получим мгновенную картину распределения скоростей жидкости, так называемое поле скоростей. В каждой точке пространства будет указан вектор скорости той частицы, которая проходит через эту точку в данный момент времени. Можно провести линию, касательная к которой указывает направление скорости частицы жидкости, проходящей в рассматриваемый момент времени через точку касания. Такая линия называется линией тока.
Если поле скоростей и соответствующие ему линии тока не меняются с течением времени, то движение жидкости называется стационарным или установившимся. В противном случае движение называет нестационарным. В первом случае скорость будет функцией только координат, v (r), во втором – функцией координат и времени, v (r, t).2
В случае нестационарного движения линии тока вообще говоря не совпадают траекториями частиц жидкости. траектория указывает путь одной и той же частицы за время ее движения, линия же тока характеризует направление движения бесконечного множества частиц, которые находятся на этой линии в рассматриваемый момент времени. Только при стационарном движении линии тока совпадаю с траекториями частиц. Для 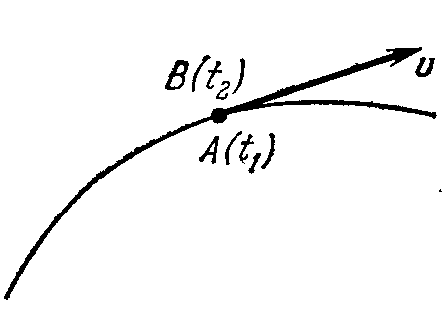 доказательства возьмем траекторию какой-нибудь произвольной частицы.
доказательства возьмем траекторию какой-нибудь произвольной частицы.
Пусть A (t 1) – положение этой частицы в момент времени t 1. Возьмем другую частицу B (t 2), которая в момент времени t 2 занимает то же положение, что и частица A в момент времени t 1. Так как движение стационарно, то есть поле скоростей одинаково в каждый момент времени, то через точку A (t 1) частица A пройдет с той же скоростью, что и частица B пройдет через эту же точку в момент времени t 2. Значит, скорость частицы B в рассматриваемой точке направлена по касательной к траектории частицы A. Так как момент времени t 2 можно выбрать произвольно, отсюда следует, что траектория частицы A является также линией тока.
Если взять некоторый произвольный замкнутый контур С и через каждую его точку в один и тот же момент времени провести линию тока, то о  ни сформируют так называемую трубку тока. Так как скорости частиц жидкости направлены по касательной к линии тока, то при течении жидкость не может пересекать боковую поверхность трубки тока.
ни сформируют так называемую трубку тока. Так как скорости частиц жидкости направлены по касательной к линии тока, то при течении жидкость не может пересекать боковую поверхность трубки тока.
Если поперечное сечение трубки тока бесконечно мало, то можно считать, что скорость жидкости одна и та же во всех точках одного и того же поперечного сечения и направлена вдоль оси трубки тока. Масса жидкости, протекающая за время dt через поперечное сечение трубки тока, определяется соотношением
 .
.
где S – площадь нормального поперечного сечения трубки.
В случае стационарного течения масса dm будет одинаковой для всех сечений трубки тока в силу закона сохранения массы или закона ненакопления вещества. Если взять два сечения, площади которых равны S 1 и S 2, то можно записать
 .
.
Если бы это равенство не соблюдалось, то масса жидкости между этими сечениями изменялась бы со временем. А это противоречит закону сохранения массы и условию стационарности движения.
Если жидкость несжимаема, то плотности в обоих сечениях одинаковы, то найденное соотношение принимает вид
 ,
,
или  .
.
Такое соотношение справедливо не только для трубки тока, но и для стационарного течения так называемых идеальных жидкостей (жидкостей, в которых не возникает внутренних сил трения) по трубам переменного сечения.
Оно называется условием неразрывности потока: при установившемся течении несжимаемой жидкости через любое сечение ее потока за равные промежутки времени протекает одинаковое количество жидкости.
Из этого соотношения видно, что скорость жидкости в одной и той же трубке тока тем больше, чем меньше ее поперечное сечение.
Уравнение Бернулли.
Изучение движения реальных жидкостей и газов, вообще говоря, представляет собой довольно сложную задачу. Для ее упрощения сначала полностью пренебрегают силами внутреннего трения, считая жидкости идеальными.
Рассмотрим стационарное течение идеальной жидкости в каком-либо консервативном силовом поле, например в поле силы тяжести.[1] Применим к этому течению закон сохранения энергии. При этом будем полностью пренебрегать теплообменом, который может происходить между частями жидкости с окружающей средой. Выделим в жидкости бесконечно узкую трубку тока и рассмотрим часть жидкости, занимающую объем MNDC.

Пусть эта часть переместилась в бесконечно близкое положение M1N1D1C1. Вычислим работу А, совершаемую при этом силами давления. Давление, действующее на боковую поверхность трубки тока, перпендикулярно к перемещению и работы не совершает. При перемещении границы MN в положение M1N1 совершается работа A 1 = p 1 S 1 l 1, где l 1 = MM1 – величина перемещения. Введя объем ∆1 V = S 1 l 1, ее можно представить в виде A 1 = p 1∆1 V или  , где
, где  — масса жидкости в объеме MNN1M1. При перемещении границы CD в положение C1D1 жидкость совершает работу против давления Р2 (или давление Р2 совершает над жидкостью отрицательную работу). Для нее, рассуждая аналогично, найдем
— масса жидкости в объеме MNN1M1. При перемещении границы CD в положение C1D1 жидкость совершает работу против давления Р2 (или давление Р2 совершает над жидкостью отрицательную работу). Для нее, рассуждая аналогично, найдем  , где
, где  — масса жидкости в объеме
— масса жидкости в объеме  . Но если движение стационарно, то масса жидкости в объеме M1N1DC не изменится, а потому из закона сохранения массы получим
. Но если движение стационарно, то масса жидкости в объеме M1N1DC не изменится, а потому из закона сохранения массы получим  . Опуская индексы у
. Опуская индексы у 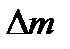 , для работы, совершаемой внешним давлением, окончательно находим
, для работы, совершаемой внешним давлением, окончательно находим

Эта работа должна быть равна приращению  полной энергии выделенной части жидкости. Ввиду стационарности течения энергия жидкости в объеме M1N1DC не изменилась. Поэтому величина
полной энергии выделенной части жидкости. Ввиду стационарности течения энергия жидкости в объеме M1N1DC не изменилась. Поэтому величина  равна разности энергий массы жидкости
равна разности энергий массы жидкости 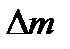 в положениях CDD1С1 и MNN1M1. Обозначая посредством ε полную энергию, приходящуюся на единицу массы жидкости, находим
в положениях CDD1С1 и MNN1M1. Обозначая посредством ε полную энергию, приходящуюся на единицу массы жидкости, находим  Приравнивая эту величину работе А и сокращая на
Приравнивая эту величину работе А и сокращая на 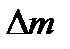 , получаем
, получаем

Отсюда следует, что вдоль одной и той же линии тока при стационарном течении идеальной жидкости величина  остается постоянной:
остается постоянной:

Это соотношение называется уравнением Даниила Бернулли (1700—1782), который впервые опубликовал его в 1738 году. При выводе уравнения Бернулли мы нигде не использовали предположения о несжимаемости жидкости. Поэтому оно справедливо и для сжимаемых жидкостей. Требуется только, чтобы жидкость была идеальной, а течение – стационарным.
Если жидкость несжимаемая, то вся энергия ε складывается из кинетической энергии единицы массы жидкости  и ее потенциальной энергии gh в поле тяжести. В этом случае уравнение Бернулли принимает вид
и ее потенциальной энергии gh в поле тяжести. В этом случае уравнение Бернулли принимает вид

Подчеркнем, что это постоянство этой величины выполняется только вдоль одной и той же линии тока. Вообще говоря, она может меняться при переходе от одной линии тока к другой. Но могут быть и такие случаи, где постоянная Бернулли одна и та же для всего потока жидкости. Рассмотрим один довольно часто встречающийся частный случай. Допустим, что все линии тока начинаются или оканчиваются в такой области, где жидкость практически находится в состоянии покоя. Возьмем одну из точек линии тока в этой области. Тогда в уравнении Бернулли следует считать v = 0 и мы получим
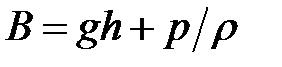 .
.
Но во всей области, где жидкость покоится, должно выполняться условие  , так как давление в покоящейся жидкости одинаково (при соответствующем введении начала координат направления оси это представляет собой условие равновесия). Поэтому в рассматриваемом случае постоянная Бернулли для всех линий тока будет одинаковой.
, так как давление в покоящейся жидкости одинаково (при соответствующем введении начала координат направления оси это представляет собой условие равновесия). Поэтому в рассматриваемом случае постоянная Бернулли для всех линий тока будет одинаковой.
Допустим теперь, что тонкая трубка тока имеет переменное поперечное сечение, а ось ее горизонтальна. (Примером может служить горизонтальная труба переменного сечения, по которой течет жидкость). Тогда h — const, и уравнение Бернулли принимает вид

 Отсюда видно, что давление больше там, где меньше скорость v, и наоборот. С другой стороны, согласно соотношению
Отсюда видно, что давление больше там, где меньше скорость v, и наоборот. С другой стороны, согласно соотношению  , скорость v минимальна там, где максимально сечение трубки. Значит, в широких частях трубки давление максимально, а в узких — минимально. Такой результат является непосредственным следствием второго закона Ньютона. Действительно, когда жидкость из широкой части течет в узкую, то скорость ее возрастает. Значит, ускорение направлено в сторону течения, т.е. на рис. слева направо. Это ускорение сообщается разностью давлений, действующих на рассматриваемую часть жидкости слева и справа. Следовательно, давление слева, т. е. в более широкой части трубки, должно быть больше, чем справа, где трубка уже.
, скорость v минимальна там, где максимально сечение трубки. Значит, в широких частях трубки давление максимально, а в узких — минимально. Такой результат является непосредственным следствием второго закона Ньютона. Действительно, когда жидкость из широкой части течет в узкую, то скорость ее возрастает. Значит, ускорение направлено в сторону течения, т.е. на рис. слева направо. Это ускорение сообщается разностью давлений, действующих на рассматриваемую часть жидкости слева и справа. Следовательно, давление слева, т. е. в более широкой части трубки, должно быть больше, чем справа, где трубка уже.
Рассмотрим несколько примеров, иллюстрирующих следствия из уравнения Бернулли.
Пульверизатор.
Возьмем трубку с суживающимся наконечником и будем продувать через нее воздух. Давление воздуха в узкой части наконечника и в выходящей из него струе будет меньше атмосферного.
Поднесем теперь струю воздуха к верхнему концу стеклянной трубки, нижний конец которой погружен в воду, а верхний оканчивается узким наконечником (рис. 2.3, а). Вода в стеклянной трубке будет подниматься, разбрызгиваться и увлекаться струей воздуха. На этом принципе основано устройство пульверизатора.

Рис. 2.3.
Если трубка, по которой продувается воздух, не снабжена узким наконечником, а имеет постоянное поперечное сечение (рис. 2.3, б), то поднятие воды и разбрызгивание не происходит. Если, однако, такую трубку поднести вплотную к наконечнику трубки, погруженной в воду, так, чтобы между ними образовался узкий зазор (рис.2.3, в), то вода опять поднимается и разбрызгивается. Зазор между трубками выполняет роль узкого наконечника, понижающего давление воздуха в струе.
Рассмотрим другой пример.
Если два слегка изогнутых листа твердой бумаги подвесить на горизонтальных проволоках (рис. 2.4) и продувать между ними воздух, то они притягиваются друг к другу. Дело в том, что давление воздуха Р между листами в наиболее узком месте


Рис. 2.5.
становится меньше атмосферного Р0, и наружное атмосферное давление прижимает листы друг к другу. Можно также подвесить на небольшом расстоянии друг от друга две стеклянные колбы. При продувании воздуха между ними колбы начинают стучать, сталкиваясь друг с другом. Притяжение такого же типа наблюдается между двумя кораблями, когда они идут параллельным курсом на небольшом расстоянии друг от друга. Это легко объяснить, если перейти в систему отсчета, в которой корабли покоятся, а вода течет между ними. Описанное явление не раз было причиной столкновения судов и приводило к авариям.
3. Формула Торричелли. Кавитация. Форма струи жидкости
Уравнение Бернулли имеет самое широкое применение на практике. В качестве первого примера рассмотрим стационарное истечение идеальной несжимаемой жидкости из сосуда (рис.2.6). Если полагать, что сосуд достаточно велик, а отверстие мало, то можно считать, что при истечении уровень жидкости не изменяется заметно в течение достаточно продолжительного промежутка времени. Пусть на поверхность жидкости в сосуде действует давление  (например, атмосферное). Будем также полагать, что струя вытекает в пространство, где внешнее давление также равно
(например, атмосферное). Будем также полагать, что струя вытекает в пространство, где внешнее давление также равно  (истечение в атмосферу). Обобщение на различные давления не составляет труда. Проведем некоторую гипотетическую линию тока и выберем на ней две точки: одну на поверхности жидкости в сосуде (точка 1), другую внутри отверстия (точка 2).
(истечение в атмосферу). Обобщение на различные давления не составляет труда. Проведем некоторую гипотетическую линию тока и выберем на ней две точки: одну на поверхности жидкости в сосуде (точка 1), другую внутри отверстия (точка 2).
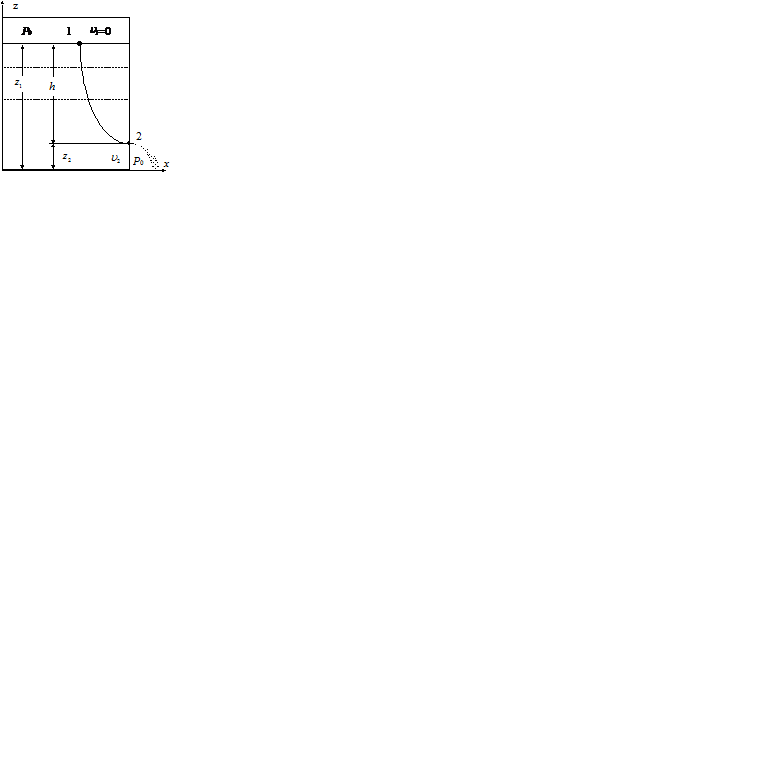 Рис.2.6. Рис.2.6.
| Тогда для этой линии тока можно записать уравнение Бернулли:   Поскольку поверхность жидкости в сосуде предполагается неподвижной Поскольку поверхность жидкости в сосуде предполагается неподвижной  ), из последнего равенства следует: Это соотношение называется формулой Торричелли. Заметим, что такую же скорость приобретает тело, которое падает в пустоте с высоты h. С помощью формулы Торричелли, можно оценить, за какое время жидкость полностью истечет из сосуда. ), из последнего равенства следует: Это соотношение называется формулой Торричелли. Заметим, что такую же скорость приобретает тело, которое падает в пустоте с высоты h. С помощью формулы Торричелли, можно оценить, за какое время жидкость полностью истечет из сосуда.
|
Задача о вытекании жидкости из сосуда.
Пусть внизу сосуда имеется отверстие площадью S0, а в самом сосуде начальная высота уровня жидкости равна h 0. Нужно найти зависимость высоты уровня жидкости от времени. За какое время жидкость полностью вытечет из сосуда?
Применим формулу Торричелли для скорости жидкости:
 .
.
Тогда объем жидкости, вытекающий в секунду из сосуда, может быть рассчитан, как
 .
.
Но с другой стороны, объем равен:
 .
.
Таким образом, получаем дифференциальное уравнение:
.
Разделяем переменные и интегрируем:
 .
.
 .
.
Используя начальные условия, получим:
 ,
,
 ,
,
 .
.
Тогда время, за которое вся жидкость выльется из сосуда, будет равно:
 .
.
Кавитация
Если увеличивать скорость движения жидкости по трубе или, при том же самом расходе жидкости уменьшить самое узкое сечение трубы, то можно в этом сечении получить отрицательное давление. Действительно, из уравнения Бернулли и закона не накопления вещества в сечениях S 1 и Smin трубы можно записать

Из этих уравнений легко получить выражение для минимального давления  в самом узком сечении трубы
в самом узком сечении трубы  :
:

Из данного соотношения видно, что если второе слагаемое в правой части по абсолютной величине будет больше, чем  , то минимальное давление окажется «отрицательным», т.е. частицы жидкости, проходящее сечение трубы с «отрицательным» давлением будут подвергаться растяжению (такую жидкость называют «растянутой»). Однако, как отмечалось выше, жидкость не может находиться в растянутом состоянии длительное время. Она «вскипит» или, как говорят, сплошность жидкости нарушится в результате выделения пузырьков растворенного в ней газа. Так как при падении давления до «отрицательных» значений в жидкости выделяются пузырьки, заполненные паром жидкости или газом, растворённым в ней, или тем и другим в той или иной концентрации, то возникает так называемое явление кавитации, т.е. явление нарушения сплошности движущейся среды.
, то минимальное давление окажется «отрицательным», т.е. частицы жидкости, проходящее сечение трубы с «отрицательным» давлением будут подвергаться растяжению (такую жидкость называют «растянутой»). Однако, как отмечалось выше, жидкость не может находиться в растянутом состоянии длительное время. Она «вскипит» или, как говорят, сплошность жидкости нарушится в результате выделения пузырьков растворенного в ней газа. Так как при падении давления до «отрицательных» значений в жидкости выделяются пузырьки, заполненные паром жидкости или газом, растворённым в ней, или тем и другим в той или иной концентрации, то возникает так называемое явление кавитации, т.е. явление нарушения сплошности движущейся среды.
Явление кавитации играет очень важную роль в инженерной практике. Дело в том, что пузырьки газа, проходя самое узкое сечение трубы, попадают далее в область более высокого давления и схлопываются. При этом схлопывание пузырька происходит не симметрично, образуется кумулятивная (направленная) струя.
Если такие пузырьки попадают на поверхность тела, то при их схлопывании возникают довольно значительные локальные давления, которые, в свою очередь, приводят к эрозии, т.е. разрушению, материала поверхности. Аналогичные явления возникают при быстром движении тел в жидкости, например, при вращении гребных винтов пароходов или лопаток гидротурбин. При этом так же образуются области «растянутой» жидкости, в которых выделяются пузырьки. Кавитация приводит к чрезвычайно быстрому их износу и выходу из строя и по настоящее время является предметом интенсивного изучения. Практически можно считать, что кавитация возникает тогда, когда в жидкости давление падает до давления насыщенных паров при данной температуре, т.е. когда 
Форма струи жидкости
Найдем форму струи жидкости, вытекающей из вертикальной трубы круглого сечения радиуса R. Будем пренебрегать вязкостью жидкости, а так же распределением скорости жидкости по радиусу.
Рис.2.7.
Такое предположение обусловлено тем, что на границе струи и воздуха скорость жидкости не равна нулю, а трением жидкости о воздух можно пренебречь. Тогда запишем уравнения непрерывности и Бернулли для произвольного сечения жидкости:
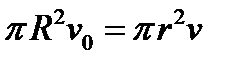 ,
,
 .
.
Поскольку на внешней границе струи давление должно быть равно атмосферному, то, следовательно, давление по всей длине струи одинаково. Выразим скорость из уравнения непрерывности
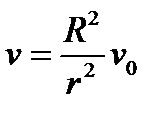 .
.
В результате получим:
 .
.
Таким образом, видим, что радиус струи уменьшается в зависимости от расстояния от входа в нее. Будет ли верна эта зависимость для очень тонких струй? Как мы знаем из опыта, каждая струю на определенной высоте распадается на капли. При этом необходимо будет принимать во внимание поверхностное натяжение жидкости.
4. Вязкость.
В реальных жидкостях, в отличие от упрощенной модели идеальной жидкости, помимо нормальных давлений на границах движущихся элементов действуют еще касательные силы внутреннего трения, или вязкость. Убедиться в существовании таких сил можно на простейших примерах.
Во-первых, из уравнения Бернулли следует, что если жидкость будет стационарно течь по горизонтальной трубе постоянного поперечного сечения, то давление вдоль всей трубы будет постоянным. На самом же деле, чтобы поддерживать течение стационарным, на концах трубы необходимо поддерживать постоянную разность давлений. Это связано с необходимостью компенсировать силы внутреннего трения, возникающие при течении.
В качестве другого примера рассмотрим поведение жидкости во вращающемся сосуде. Если вертикальный цилиндрический сосуд, заполненный жидкостью, привести в равномерное вращение относительно своей оси, то жидкость постепенно тоже придет во вращение. Сначала начинают вращаться слои жидкости, прилегающие к стенкам сосуда. Затем вращение передается внутренним слоям, пока вся жидкость не начнет равномерно вращаться как твердое тело. Пока движение не установилось, происходит непрерывная передача вращения от сосуда к жидкости, и далее от наружных слоев жидкости к внутренним. Такая передача движения или импульса была бы не возможна без касательных сил, действующих между жидкостью и стенкой сосуда, а также между слоями жидкости, вращающимися с различными угловыми скоростями. Эти касательные силы называют силами трения, внутреннего, или вязкого, если они действуют между слоями жидкости, и внешнего, если они действуют между жидкостью и стенками сосуда.
 Чтобы найти количественные законы вязкого трения, рассмотрим простейший пример. Возьмем две параллельные бесконечно длинные пластинки, между которыми находится жидкость. В практическом смысле пластинки можно считать бесконечно длинными, если их длина и ширина много больше расстояния между ними. Пусть нижняя пластинка неподвижна, а верхняя пластинка движется относительно нижней с постоянной скоростью v 0. Чтобы поддерживать движение пластинки постоянным, очевидно, к ней нужно приложить постоянную силу F, направленную в сторону движения. Как мы уже рассматривали в примере с вращающимся сосудом, движение верхней пластинки будет передаваться жидкости, а затем и нижней пластинке. Поэтому, чтобы удержать ее в покое, на нее должна действовать такая же, но противоположно направленная сила. Ньютон экспериментально установил, что величина силы F пропорциональна скорости v 0, площади S пластинки и обратно пропорциональна расстоянию h между пластинками:
Чтобы найти количественные законы вязкого трения, рассмотрим простейший пример. Возьмем две параллельные бесконечно длинные пластинки, между которыми находится жидкость. В практическом смысле пластинки можно считать бесконечно длинными, если их длина и ширина много больше расстояния между ними. Пусть нижняя пластинка неподвижна, а верхняя пластинка движется относительно нижней с постоянной скоростью v 0. Чтобы поддерживать движение пластинки постоянным, очевидно, к ней нужно приложить постоянную силу F, направленную в сторону движения. Как мы уже рассматривали в примере с вращающимся сосудом, движение верхней пластинки будет передаваться жидкости, а затем и нижней пластинке. Поэтому, чтобы удержать ее в покое, на нее должна действовать такая же, но противоположно направленная сила. Ньютон экспериментально установил, что величина силы F пропорциональна скорости v 0, площади S пластинки и обратно пропорциональна расстоянию h между пластинками:
 .
.
Здесь η – коэффициент, называемый коэффициентом внутреннего трения или коэффициентом вязкости жидкости. (Посчитать размерность этого коэффициента.) Коэффициент вязкости не зависит от материала пластинок, является характеристикой жидкости и для различных жидкостей имеет различные значения. Для определенной жидкости его значение зависит от параметров, характеризующих ее внутреннее состояние, в первую очередь, от температуры.
Если нижняя пластинка не неподвижна, а обе они движутся равномерно параллельно друг другу, то можно написать более общую формулу
 ,
,
где v 1 – скорость движения нижней пластинки, v 2 – верхней. Чтобы убедиться в этом, достаточно перейти в систему отсчета, в которой нижняя пластинка покоится.
Вообще говоря, при равномерном движении верхней пластинки жидкость должна действовать на нее с силой –F, чтобы полная сила, приложенная к пластинке, обращалась в нуль. Сама пластинка, соответственно, действует на жидкость с силой +F. Аналогично и с нижней пластинкой, она будет действовать на жидкость с силой –F. Кроме того, экспериментально установлено, что жидкость, обладающая вязкостью, прилипает к поверхности тела, которое она обтекает. То есть скорости движения частиц жидкости относительно поверхности обтекаемого тела, на которой они находятся, равны нулю. Поэтому в полученной нами формуле силы можно считать приложенными не к пластинкам, а к границам заключенного между ними слоя жидкости, точно так же скорости v 1 и v 2 можно отождествить не с пластинками, а со скоростями движения тех же границ жидкости. Тем самым, для введения понятия коэффициента вязкости надобность в пластинках отпадает.
Чтобы обобщить последнюю формулу, допустим, что жидкость течет вдоль оси x, причем скорость течения зависит только от координаты y:
 ,
,  .
.
Вырежем мысленно жидкий слой, ограниченный бесконечно близкими плоскостями, перпендикулярными к оси y. Пусть эти плоскости пересекаю ось y в точках с координатами y и y+dy. Обозначим τyx касательную силу, действующую на единицу площади верхней границы такого слоя со стороны вышележащей жидкости. Первый индекс указывает, какой оси перпендикулярна рассматриваемая площадка, то есть направление внешней нормали к этой плоскости, второй индекс указывает направление действия рассматриваемой силы. Тогда можно записать, обобщая полученную ранее формулу, что
 .
.
Такая формула будет справедлива не только для равномерного течения, но и для течения, скорость vx которого зависит от времени. Очевидно, что на нижней границе выделенного слоя будет действовать касательное напряжение τ-yx, направленное в противоположную сторону. Оно бесконечно мало отличается от τyx ввиду бесконечной малости толщины рассматриваемого слоя. (τyx = – τ-yx).
 Рассмотрим теперь параллелепипед в том же потоке жидкости, ребра которого параллельны координатным осям. Чтобы движение выделенного элемента оставалось параллельным оси, нужно, чтобы момент действующих на него сил был равен нулю. Поэтому на его боковых основаниях, перпендикулярных потоку, также должны действовать касательные напряжения, причем
Рассмотрим теперь параллелепипед в том же потоке жидкости, ребра которого параллельны координатным осям. Чтобы движение выделенного элемента оставалось параллельным оси, нужно, чтобы момент действующих на него сил был равен нулю. Поэтому на его боковых основаниях, перпендикулярных потоку, также должны действовать касательные напряжения, причем
 .
.
Таким образом, касательные напряжения действуют не только в плоскостях, параллельных течению, но и в плоскостях, перпендикулярных ему.
Допустим теперь, что жидкость течет не параллельным потоком, а произвольным образом. Тогда из всех возникающих касательных и нормальных напряжений мы получим так называемый тензор вязких напряжений. Если мы примем, что касательные составляющие этого тензора зависит только от скоростей в различных слоях жидкости, то есть от первой производной скорости, и не зависит от более высоких порядков производных. В таком приближении касательные напряжения являются линейными однородными функциями производных
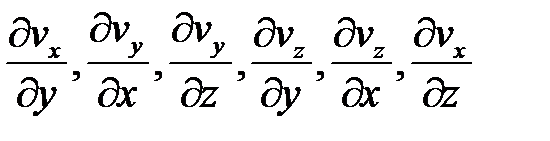 .
.
Если бы из этих шести производных на поверхности рассмотренного нами элемента отлична от нуля была бы только производная  , то вдоль оси x действовало бы касательно напряжение
, то вдоль оси x действовало бы касательно напряжение 
|
|
|



 ). В очень большом сосуде при истечении жидкости из маленького отверстия скорость жидкости можно считать равной нулю (
). В очень большом сосуде при истечении жидкости из маленького отверстия скорость жидкости можно считать равной нулю ( ). Следовательно, в верхней точки жидкости (где высота – h, а
). Следовательно, в верхней точки жидкости (где высота – h, а  ), то есть в левой части уравнения Бернулли, получаем величину
), то есть в левой части уравнения Бернулли, получаем величину  .
. , а
, а  ), то есть в правой части уравнения Бернулли, получаем величину
), то есть в правой части уравнения Бернулли, получаем величину  .
.
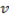 ) истечения жидкости из маленького отверстия:
) истечения жидкости из маленького отверстия:  .
. .
. .
.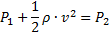
 бьет в неподвижную стену перпендикулярно ее поверхности. Найдите давление, которое производит жидкость на стену в точке, находящейся на оси струи. Атмосферное давление
бьет в неподвижную стену перпендикулярно ее поверхности. Найдите давление, которое производит жидкость на стену в точке, находящейся на оси струи. Атмосферное давление  , плотность жидкости
, плотность жидкости 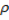 .
. Линии тока жидкости - это линии, в каждой точке которых вектор скорости частиц жидкости направлен по касательной (рис. 4).
Линии тока жидкости - это линии, в каждой точке которых вектор скорости частиц жидкости направлен по касательной (рис. 4). Т.к. жидкость несжимаема, через S1 и S2 пройдет за Dt одинаковая масса жидкости (рис. 5).
Т.к. жидкость несжимаема, через S1 и S2 пройдет за Dt одинаковая масса жидкости (рис. 5).
 - уравнение неразрывности струи или теорема Эйлера.
- уравнение неразрывности струи или теорема Эйлера. Теорема о неразрывности широко применяется при расчетах, связанных с подачей жидкого топлива в двигатели по трубам переменного сечения. Зависимость скорости потока от сечения канала, по которому течет жидкость или газ, используется при конструировании сопла ракетного двигателя. В месте сужения сопла (рис. 6) скорость истекающих из ракеты продуктов сгорания резко возрастает, а давление падает, благодаря чему возникает дополнительная сила тяги.
Теорема о неразрывности широко применяется при расчетах, связанных с подачей жидкого топлива в двигатели по трубам переменного сечения. Зависимость скорости потока от сечения канала, по которому течет жидкость или газ, используется при конструировании сопла ракетного двигателя. В месте сужения сопла (рис. 6) скорость истекающих из ракеты продуктов сгорания резко возрастает, а давление падает, благодаря чему возникает дополнительная сила тяги. Пусть жидкость движется в поле сил тяжести так, что в данной точке пространства величина и направление скорости жидкости остаются постоянными. Такое течение называется стационарным. В стационарно текущей жидкости кроме сил тяжести действуют еще и силы давления. Выделим в стационарном потоке участок трубки тока, ограниченный сечениями S1 и S2 (рис.7)
Пусть жидкость движется в поле сил тяжести так, что в данной точке пространства величина и направление скорости жидкости остаются постоянными. Такое течение называется стационарным. В стационарно текущей жидкости кроме сил тяжести действуют еще и силы давления. Выделим в стационарном потоке участок трубки тока, ограниченный сечениями S1 и S2 (рис.7) , а S2 - в положение 2', пройдя путь
, а S2 - в положение 2', пройдя путь  . В силу неразрывности струи выделенные объемы (и их массы) одинаковы:
. В силу неразрывности струи выделенные объемы (и их массы) одинаковы: ,
,  .
. настолько малыми, чтобы всем точкам каждого из заштрихованных объемов можно было приписать одно и то же значение скорости, давления и высоты. Тогда приращение энергии равно:
настолько малыми, чтобы всем точкам каждого из заштрихованных объемов можно было приписать одно и то же значение скорости, давления и высоты. Тогда приращение энергии равно:
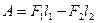
 направлена в сторону, противоположную перемещению
направлена в сторону, противоположную перемещению  ,
,  ,
, ,
, ,
, .
. ,
, (1)
(1) ,
, 
 доказательства возьмем траекторию какой-нибудь произвольной частицы.
доказательства возьмем траекторию какой-нибудь произвольной частицы. ни сформируют так называемую трубку тока. Так как скорости частиц жидкости направлены по касательной к линии тока, то при течении жидкость не может пересекать боковую поверхность трубки тока.
ни сформируют так называемую трубку тока. Так как скорости частиц жидкости направлены по касательной к линии тока, то при течении жидкость не может пересекать боковую поверхность трубки тока. .
. .
. ,
, .
.
 , где
, где  — масса жидкости в объеме MNN1M1. При перемещении границы CD в положение C1D1 жидкость совершает работу против давления Р2 (или давление Р2 совершает над жидкостью отрицательную работу). Для нее, рассуждая аналогично, найдем
— масса жидкости в объеме MNN1M1. При перемещении границы CD в положение C1D1 жидкость совершает работу против давления Р2 (или давление Р2 совершает над жидкостью отрицательную работу). Для нее, рассуждая аналогично, найдем  , где
, где  — масса жидкости в объеме
— масса жидкости в объеме  . Но если движение стационарно, то масса жидкости в объеме M1N1DC не изменится, а потому из закона сохранения массы получим
. Но если движение стационарно, то масса жидкости в объеме M1N1DC не изменится, а потому из закона сохранения массы получим  . Опуская индексы у
. Опуская индексы у 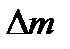 , для работы, совершаемой внешним давлением, окончательно находим
, для работы, совершаемой внешним давлением, окончательно находим
 полной энергии выделенной части жидкости. Ввиду стационарности течения энергия жидкости в объеме M1N1DC не изменилась. Поэтому величина
полной энергии выделенной части жидкости. Ввиду стационарности течения энергия жидкости в объеме M1N1DC не изменилась. Поэтому величина  Приравнивая эту величину работе А и сокращая на
Приравнивая эту величину работе А и сокращая на 
 остается постоянной:
остается постоянной:
 и ее потенциальной энергии gh в поле тяжести. В этом случае уравнение Бернулли принимает вид
и ее потенциальной энергии gh в поле тяжести. В этом случае уравнение Бернулли принимает вид
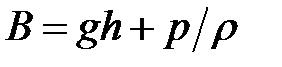 .
. , так как давление в покоящейся жидкости одинаково (при соответствующем введении начала координат направления оси это представляет собой условие равновесия). Поэтому в рассматриваемом случае постоянная Бернулли для всех линий тока будет одинаковой.
, так как давление в покоящейся жидкости одинаково (при соответствующем введении начала координат направления оси это представляет собой условие равновесия). Поэтому в рассматриваемом случае постоянная Бернулли для всех линий тока будет одинаковой.
 Отсюда видно, что давление больше там, где меньше скорость v, и наоборот. С другой стороны, согласно соотношению
Отсюда видно, что давление больше там, где меньше скорость v, и наоборот. С другой стороны, согласно соотношению  , скорость v минимальна там, где максимально сечение трубки. Значит, в широких частях трубки давление максимально, а в узких — минимально. Такой результат является непосредственным следствием второго закона Ньютона. Действительно, когда жидкость из широкой части течет в узкую, то скорость ее возрастает. Значит, ускорение направлено в сторону течения, т.е. на рис. слева направо. Это ускорение сообщается разностью давлений, действующих на рассматриваемую часть жидкости слева и справа. Следовательно, давление слева, т. е. в более широкой части трубки, должно быть больше, чем справа, где трубка уже.
, скорость v минимальна там, где максимально сечение трубки. Значит, в широких частях трубки давление максимально, а в узких — минимально. Такой результат является непосредственным следствием второго закона Ньютона. Действительно, когда жидкость из широкой части течет в узкую, то скорость ее возрастает. Значит, ускорение направлено в сторону течения, т.е. на рис. слева направо. Это ускорение сообщается разностью давлений, действующих на рассматриваемую часть жидкости слева и справа. Следовательно, давление слева, т. е. в более широкой части трубки, должно быть больше, чем справа, где трубка уже.


 (например, атмосферное). Будем также полагать, что струя вытекает в пространство, где внешнее давление также равно
(например, атмосферное). Будем также полагать, что струя вытекает в пространство, где внешнее давление также равно  Рис.2.6.
Рис.2.6.

 Поскольку поверхность жидкости в сосуде предполагается неподвижной
Поскольку поверхность жидкости в сосуде предполагается неподвижной  ), из последнего равенства следует: Это соотношение называется формулой Торричелли. Заметим, что такую же скорость приобретает тело, которое падает в пустоте с высоты h. С помощью формулы Торричелли, можно оценить, за какое время жидкость полностью истечет из сосуда.
), из последнего равенства следует: Это соотношение называется формулой Торричелли. Заметим, что такую же скорость приобретает тело, которое падает в пустоте с высоты h. С помощью формулы Торричелли, можно оценить, за какое время жидкость полностью истечет из сосуда.
 .
. .
. .
. .
. .
. ,
, ,
, .
. .
.
 в самом узком сечении трубы
в самом узком сечении трубы  :
:
 , то минимальное давление окажется «отрицательным», т.е. частицы жидкости, проходящее сечение трубы с «отрицательным» давлением будут подвергаться растяжению (такую жидкость называют «растянутой»). Однако, как отмечалось выше, жидкость не может находиться в растянутом состоянии длительное время. Она «вскипит» или, как говорят, сплошность жидкости нарушится в результате выделения пузырьков растворенного в ней газа. Так как при падении давления до «отрицательных» значений в жидкости выделяются пузырьки, заполненные паром жидкости или газом, растворённым в ней, или тем и другим в той или иной концентрации, то возникает так называемое явление кавитации, т.е. явление нарушения сплошности движущейся среды.
, то минимальное давление окажется «отрицательным», т.е. частицы жидкости, проходящее сечение трубы с «отрицательным» давлением будут подвергаться растяжению (такую жидкость называют «растянутой»). Однако, как отмечалось выше, жидкость не может находиться в растянутом состоянии длительное время. Она «вскипит» или, как говорят, сплошность жидкости нарушится в результате выделения пузырьков растворенного в ней газа. Так как при падении давления до «отрицательных» значений в жидкости выделяются пузырьки, заполненные паром жидкости или газом, растворённым в ней, или тем и другим в той или иной концентрации, то возникает так называемое явление кавитации, т.е. явление нарушения сплошности движущейся среды.
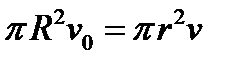 ,
, .
.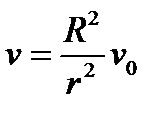 .
. .
. Чтобы найти количественные законы вязкого трения, рассмотрим простейший пример. Возьмем две параллельные бесконечно длинные пластинки, между которыми находится жидкость. В практическом смысле пластинки можно считать бесконечно длинными, если их длина и ширина много больше расстояния между ними. Пусть нижняя пластинка неподвижна, а верхняя пластинка движется относительно нижней с постоянной скоростью v 0. Чтобы поддерживать движение пластинки постоянным, очевидно, к ней нужно приложить постоянную силу F, направленную в сторону движения. Как мы уже рассматривали в примере с вращающимся сосудом, движение верхней пластинки будет передаваться жидкости, а затем и нижней пластинке. Поэтому, чтобы удержать ее в покое, на нее должна действовать такая же, но противоположно направленная сила. Ньютон экспериментально установил, что величина силы F пропорциональна скорости v 0, площади S пластинки и обратно пропорциональна расстоянию h между пластинками:
Чтобы найти количественные законы вязкого трения, рассмотрим простейший пример. Возьмем две параллельные бесконечно длинные пластинки, между которыми находится жидкость. В практическом смысле пластинки можно считать бесконечно длинными, если их длина и ширина много больше расстояния между ними. Пусть нижняя пластинка неподвижна, а верхняя пластинка движется относительно нижней с постоянной скоростью v 0. Чтобы поддерживать движение пластинки постоянным, очевидно, к ней нужно приложить постоянную силу F, направленную в сторону движения. Как мы уже рассматривали в примере с вращающимся сосудом, движение верхней пластинки будет передаваться жидкости, а затем и нижней пластинке. Поэтому, чтобы удержать ее в покое, на нее должна действовать такая же, но противоположно направленная сила. Ньютон экспериментально установил, что величина силы F пропорциональна скорости v 0, площади S пластинки и обратно пропорциональна расстоянию h между пластинками: .
. ,
, ,
,  .
. .
. Рассмотрим теперь параллелепипед в том же потоке жидкости, ребра которого параллельны координатным осям. Чтобы движение выделенного элемента оставалось параллельным оси, нужно, чтобы момент действующих на него сил был равен нулю. Поэтому на его боковых основаниях, перпендикулярных потоку, также должны действовать касательные напряжения, причем
Рассмотрим теперь параллелепипед в том же потоке жидкости, ребра которого параллельны координатным осям. Чтобы движение выделенного элемента оставалось параллельным оси, нужно, чтобы момент действующих на него сил был равен нулю. Поэтому на его боковых основаниях, перпендикулярных потоку, также должны действовать касательные напряжения, причем .
.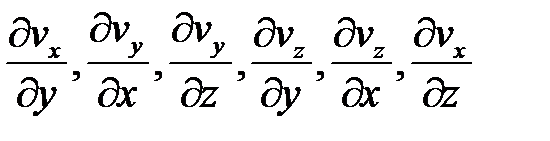 .
. , то вдоль оси x действовало бы касательно напряжение
, то вдоль оси x действовало бы касательно напряжение 


