Множество. Подмножество. Универсальное множество

1. Множество – одно из первоначальных, наиболее общих понятий в математике, таких как число, точка, которые принимают без определения.

Множеством называют совокупность каких-либо объектов (предметов, явлений) произвольной природы, которые в данном случае рассматриваются совместно: можно говорить о множестве людей, стран, автомобилей, слов, книг, точек пространства, моментов времени, чисел, функций, геометрических фигур и т.д.

Объекты, составляющие множество, называются его элементами. Обозначение а Î А читается так: «элемент а является элементом множества А», или «элемент а принадлежит множеству А»; например, обозначая символом N множество натуральных (т.е. целых положительных) чисел, можно записать соотношение 6 Î N. Если H – множество дней недели, то «вторник» Î Н. Аналогично, запись b Ï B означает, что объект b не принадлежит множеству B, т.е. не является его элементом: например, 3.14 Ï N, -2 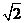Ï N, Ï N.

Термин «множество» отличается от понятия количества: говоря о множестве, мы имеем в виду прежде всего его состав, т.е. из каких элементов оно состоит; количество элементов является одной из важных его характеристик. По числу элементов множества делятся на конечные и бесконечные. Число элементов конечного множества А обозначается ½ А ½. Так, если H – множество дней недели, то ½ H ½ = 7. Иногда бывает трудно определить, содержит ли то или иное множество (например, множество корней какого-либо уравнения) хотя бы один элемент. Поэтому полезным является понятие пустого множества, не содержащего ни одного элемента. Оно обозначается символом Æ; его роль подобна роли числа 0 в арифметике.

Задать множество – значит определить, какие элементы в него входят. Один из способов задания конечного множества – прямое перечисление элементов; например:

Ц = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9},

T = {1, 3, 7, 9, 21, 63},

L = {+, –, *, /},

G = {Англия, Шотландия, Уэльс, Сев. Ирландия},

I = {гелий, неон, аргон, криптон, ксенон, радон}.

В применяемых обозначениях фигурные скобки показывают, что перечисленные элементы объединены в одно целое – множество А.

Перечислением задавать множество не всегда удобно, а подчас и невозможно, даже для конечных множеств. Понятно, что нельзя перечислить все элементы бесконечного множества. Более общий способ: задание множества характеристическим свойством его элементов,
т.е. условием, которому удовлетворяют все элементы множества и не удовлетворяют другие объекты. Так, в вышеприведенных примерах множество Ц можно определить как множество арабских цифр; Т – как множество делителей числа 63; L – как множество знаков арифметических действий; G – как множество административных единиц, составляющих Великобританию; I – как множество инертных газов.

Для задания множества A характеристическим свойством применяют обозначение
A = { x: p (x)} (читается: A есть множество элементов х, удовлетворяющих условию p (x). Например, A = { x: x ² > 1} означает множество чисел, квадрат которых больше 1. При этом имеется в виду, что свойство p (x) выделяет элементы множества A из некоторого универсального множества U.

В нашем примере должно быть, например, указано, что A состоит из действительных чисел или из целых чисел и т.п. Употребляется и такая запись: A = { x Î U: p(x)}, т.е. A есть множество таких элементов из универсального множества U, которые удовлетворяют условию p (x). Обычно универсальное множество U в каждом случае подразумевается или специально указывается.

В другом рассмотрении универсальным может быть другое множество. Так, обозначая множество действительных чисел R, а множество целых чисел Z (стандартные в математическом анализе обозначения), можно записать в первом случае A ₁ = { x Î R: x ² > 1}, а во втором случае
A ₂ = { x Î Z: x ² > 1}. В примере I универсальным можно считать множество элементов периодической системы Д.И. Менделеева.

Примеры. Множество Ч четных целых чисел: Ч = { n Î Z: n = 2k}; множество R₊ положительных действительных чисел: R ₊ = {x Î R: x > 0}. Множество I может быть определено и так: {элементы периодической системы, атомы которых имеют 8 электронов на внешней орбите}.

В геометрии множество всех точек, обладающих тем или иным свойством, называют геометрическим местом точек. Например:

(а) окружность есть геометрическое место точек плоскости, находящихся на одинаковом расстоянии от некоторой точки (называемой центром);

(б) перпендикуляр, проведенный через середину отрезка есть геометрическое место точек плоскости, равноудаленных от его концов.

В трехмерном пространстве (т.е. при другом универсальном множестве) множество точек, определяемое тем же свойством, что в примере (а), представляет собой сферу, а множество точек со свойством примера (б) есть плоскость, проведенная через середину отрезка перпендикулярно ему.

2. Если каждый элемент множества A является одновременно элементом множества B, то A называется подмножеством (или частью) множества B; обозначение A Í B.

Примеры: 1. Множество жителей Москвы является подмножеством множества жителей России.

2. Множество всех квадратов является частью множества всех прямоугольников, а оно, в свою очередь – подмножество множества всех четырехугольников.

3. Множество 5-этажных домов – подмножество множества всех домов.

Множество квартир не является подмножеством множества домов. Но в множестве квартир дома подмножествами являются, например, множество квартир 1-го подъезда, множество квартир 2-го этажа, множество двухкомнатных квартир.

4. Для числовых множеств N (натуральные числа), Z (целые числа), Q (рациональные числа), R (действительные числа), С (комплексные числа) выполнены включения: N Í Z Í Q Í R Í С.

Если A Í B и одновременно B Í A, то множества A и B состоят из одних и тех же элементов и считаются равными: A = B. При этом они могут задаваться по-разному. Пример - упомянутые выше множества Ц, Т, L, G, I заданы с одной стороны перечислением, с другой стороны – характеристическим свойством.

Соотношения между множествами наглядно иллюстрируются плоскими изображениями: их называют диаграммами Венна (а также кругами Эйлера). Множество на диаграмме образно представляется внутренностью фигуры, ограниченной замкнутой линией, а элементы, не принадлежащие множеству располагаются снаружи. Взаимные расположения нескольких фигур на рис. 1.1, 1.2, 1.3, 1.4, представляющих различные множества, схематически изображают различные случаи cоотношений между множествами.

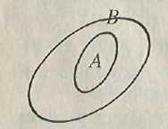
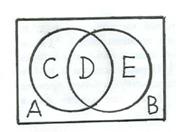
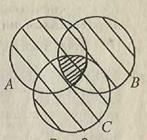
Рис. 1.1 Рис. 1.2 Рис. 1.3

Рис. 1.1 изображает соотношение A Í B.

На рис. 1.2 два множества, как говорят, «в общем положении»: три области, представляющие подмножества элементов, принадлежащих только множеству A, только множеству B и обоим множествам. Аналогично на рис. 1.3 – три множества в общем положении.