Тема: «Векторы на плоскости и в пространстве»
- Понятие вектора
Векторы находят широкое применение в математике, физике, механике и других дисциплинах, упрощают вывод многих формул, решение многих задач, доказательство теорем.
Слово «вектор» происходит от латинского слова «vector» - переноситель, несущий.
 Рассмотрим упорядоченную пару несовпадающих точек (А;В). Соединим точку А с точкой В и укажем направление от А к В. С помощью этой пары зададим преобразование плоскости (пространства). Каждой точке М плоскости (пространства) поставим в соответствие точку М1 плоскости (пространства) (ее образ), которая получится в результате следующего построения: приняв точку М за начало, проводим луч т, одинаково направленный с лучом АВ. На луче т имеется единственная точка М1, удаленная от точки М на расстояние, равное АВ.
Рассмотрим упорядоченную пару несовпадающих точек (А;В). Соединим точку А с точкой В и укажем направление от А к В. С помощью этой пары зададим преобразование плоскости (пространства). Каждой точке М плоскости (пространства) поставим в соответствие точку М1 плоскости (пространства) (ее образ), которая получится в результате следующего построения: приняв точку М за начало, проводим луч т, одинаково направленный с лучом АВ. На луче т имеется единственная точка М1, удаленная от точки М на расстояние, равное АВ.
Такое преобразование плоскости (пространства), определяемое упорядоченной парой точек называется «параллельным переносом» или «вектором».
Определение: Вектором или параллельным переносом, определяемым упорядоченной парой точек (А;В), называется преобразование плоскости (пространства), при котором каждая точка М плоскости (пространства)отображается на точку М1 плоскости (пространства) так, что луч ММ1 одинаково направлен с лучом АВ и расстояние ММ1 равно расстоянию АВ.
Определение: Нулевым вектором называется вектор, начало которого совпадает с его концом.  – нулевой вектор.
– нулевой вектор.
Вывод:
- Любой ненулевой вектор задается упорядоченной парой несовпадающих точек.
-
 Любой ненулевой вектор изображается направленным отрезком.
Любой ненулевой вектор изображается направленным отрезком.
Обозначение: 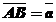
А – начало вектора 
В – конец вектора 
Определение: Направлением ненулевого вектора  называется направление луча АВ.
называется направление луча АВ.
Определение: Длиной вектора  (абсолютной величиной, модулем) называется расстояние между его началом и концом.
(абсолютной величиной, модулем) называется расстояние между его началом и концом.
Определение: Вектор, длина которого равна единице, называется единичным вектором.
Вывод:
- Любой ненулевой вектор характеризуется направлением и абсолютной величиной.
- Длина нулевого вектора равна нулю, понятие направления не определено.

Определение: Два вектора называются одинаково направленными, если они имеют одинаковые направления. (Рис. 1)
Определение: Два вектора называются равными, если они имеют одинаковые направления и длины. (Рис. 3)
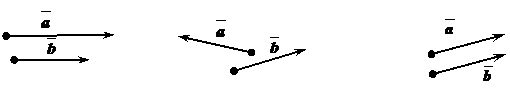 Рис. 1. Рис. 2. Рис. 3.
Рис. 1. Рис. 2. Рис. 3.


 Û
Û  и
и 
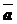 и
и 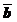
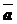 и
и 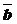
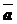 и
и 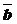
одинаково направленные векторы равные векторы
Векторы имеют одинаковую длину
Определение: Векторы, направления которых противоположны, называются противоположно направленными.
Определение: Векторы, направления которых противоположны, а длины равны, называются противоположными.
Замечание: Если 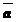 и
и 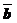 противоположные векторы, то пишут
противоположные векторы, то пишут 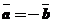 или
или 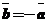 .
.
Рис. 1. Рис. 2.
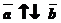
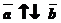 и |а | = |b |
и |а | = |b |
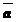 и
и 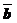
 и
и 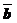
Противоположно направленные противоположные векторы
Векторы
- Действия над векторами на плоскости
2.1. 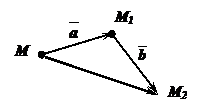 Сложение векторов.
Сложение векторов.
Пусть вектор  отображает точку М на точку М1; вектор
отображает точку М на точку М1; вектор 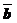 отображает точку М1 на точку М2 . Тогда существует вектор, отображающий точку М на точку М2.
отображает точку М1 на точку М2 . Тогда существует вектор, отображающий точку М на точку М2.
Определение: Пусть вектор  отображает точку М на точку М1; вектор
отображает точку М на точку М1; вектор 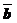 отображает точку М1 на точку М2 . Вектор, отображающий точку М на точку М2 , называется композицией векторов
отображает точку М1 на точку М2 . Вектор, отображающий точку М на точку М2 , называется композицией векторов 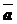 и
и 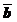 .
.
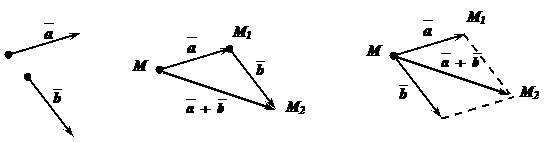 Определение: Суммой
Определение: Суммой 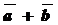 векторов
векторов 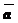 и
и 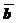 называется композиция этих векторов.
называется композиция этих векторов.
Рис. 1. Рис. 2.
«Правило треугольника»: Чтобы сложить 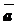 и
и 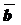 по «правилу треугольника», надо от произвольной точки плоскости отложить
по «правилу треугольника», надо от произвольной точки плоскости отложить  , от конца
, от конца 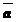 отложить
отложить 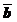 . Суммой векторов
. Суммой векторов  и
и 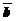 будет вектор
будет вектор 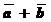 , начало которого совпадет с началом
, начало которого совпадет с началом  , конец - с концом
, конец - с концом 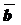 . (Рис. 1.)
. (Рис. 1.)
«Правило параллелограмма»: Чтобы сложить 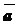 и
и 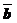 по «правилу параллелограмма», надо от произвольной точки на плоскости отложить
по «правилу параллелограмма», надо от произвольной точки на плоскости отложить  и
и 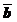 и на них, как на сторонах, построить параллелограмм. Суммой векторов
и на них, как на сторонах, построить параллелограмм. Суммой векторов  и
и 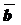 будет вектор
будет вектор 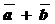 , изображаемый диагональю параллелограмма, идущей из их общего начала. (Рис. 2.)
, изображаемый диагональю параллелограмма, идущей из их общего начала. (Рис. 2.)
При сложении нескольких векторов пользуются правилом многоугольника.
«Правило многоугольника»:
Чтобы сложить несколько векторов по «правилу многоугольника», надо отложить от произвольной точки плоскости первый вектор, от конца первого вектора отложить второй вектор, от конца второго – третий и т.д. Вектором суммы будет вектор, начало которого совпадает с началом первого вектора, а конец – с концом последнего вектора.
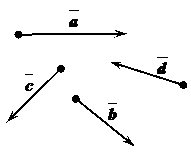 Пример:
Пример:
Дано: 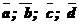
 Построить:
Построить: 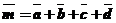
Вычитание векторов
Определение: Разностью 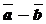 двух векторов
двух векторов 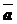 и
и 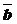 называется сумма вектора
называется сумма вектора 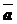 и вектора, противоположного вектору
и вектора, противоположного вектору 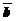 .
.
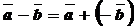
Правило: Разностью двух векторов является вектор, начало которого совпадает с концом вектора – вычитаемого, а конец – с концом вектора –уменьшаемого, если они отложены от одной точки.
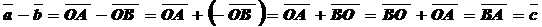
Умножение вектора на число
Определение: Произведением ненулевого вектора 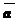 на число х, неравное нулю, называется вектор
на число х, неравное нулю, называется вектор 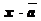 , длина которого равна
, длина которого равна 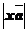 , а направление совпадает с направлением
, а направление совпадает с направлением  , если х > 0, и противоположно ему, если
, если х > 0, и противоположно ему, если
х < 0.
Замечание: Произведение нулевого вектора на любое число и произведение любого вектора на нуль по определению считается равным нулевому вектору.
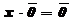 ;
; 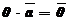 .
. 
Пример: Дано: 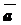 ; х1 = - 2; х2 = 3; х3 =
; х1 = - 2; х2 = 3; х3 = 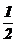 .
.
Построить: - 2 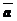 ; 3
; 3 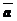 ;
; 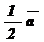 .
.
Упражнения:
1. По данным векторам 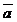 и
и 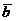 построить следующие векторы:
построить следующие векторы:
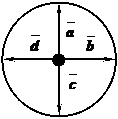

2. Найти сумму изображенных на рисунке векторов.
3. По данным векторам 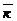 ,
, 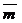 и
и 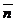 построить следующие векторы:
построить следующие векторы: 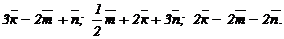
- Декартова система координат на плоскости
Векторы векторы
Вывод: Коллинеарные векторы лежат на одной прямой или на параллельных прямых.
О у – ось ординат.
Замечание: Любой вектор 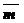 может быть единственным образом разложен по базисным векторам
может быть единственным образом разложен по базисным векторам  и
и  :
: 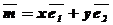 . Числа х и у называются координатами вектора
. Числа х и у называются координатами вектора 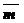 в данной декартовой системе координат.
в данной декартовой системе координат.
 Определение: Декартова система координат на плоскости называется прямоугольной, если базисные векторы взаимно перпендикулярны и единичны.
Определение: Декартова система координат на плоскости называется прямоугольной, если базисные векторы взаимно перпендикулярны и единичны.
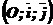 – прямоугольная декартова система координат на плоскости.
– прямоугольная декартова система координат на плоскости.
 .
.
О – начало координат;
Ох – ось абсцисс;
Оу – ось ординат.
Замечание:
1. Базисные векторы  в прямоугольной декартовой системе координат называются ортами.
в прямоугольной декартовой системе координат называются ортами.
2. Любой вектор 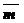 может быть единственным образом разложен по ортам
может быть единственным образом разложен по ортам  :
:  . Числа х и у являются координатами вектора
. Числа х и у являются координатами вектора 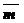 в данной прямоугольной декартовой системе координат.
в данной прямоугольной декартовой системе координат.
Упражнения:
1. Доказать, что  и
и  коллинеарны.
коллинеарны.
 2. В прямоугольнике АВСD проведены диагонали АС и ВD, пересекающиеся в точке О.
2. В прямоугольнике АВСD проведены диагонали АС и ВD, пересекающиеся в точке О. 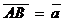 ,
,  . Выразить через
. Выразить через 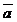 и
и 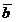 следующие векторы:
следующие векторы: 
4. Декартова система координат в пространстве
4. 1. Понятие компланарных векторов
Определение: Ненулевые вектора называются компланарными, если они параллельны одной и той же плоскости.
Замечание: Любые два вектора всегда компланарны, а три вектора могут и не быть компланарными.
Векторы  компланарны, а векторы
компланарны, а векторы  компланарными не являются.
компланарными не являются.
4. 2. Разложение вектора в пространстве по трем некомпланарным векторам
Теорема: Если даны три некомпланарных вектора 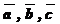 , то любой вектор
, то любой вектор  можно разложить по векторам
можно разложить по векторам 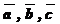 единственным образом.
единственным образом.
Дано: 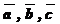 - некомпланарные векторы;
- некомпланарные векторы;
 - произвольный вектор пространства.
- произвольный вектор пространства.
Доказать: 1. 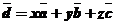 - существует;
- существует;
2. 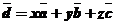 - единственное.
- единственное.
Оz – ось аппликат.
Замечание: Любой вектор  может быть единственным образом разложен по базисным векторам
может быть единственным образом разложен по базисным векторам  :
:  . Числа х, у, z называются координатами вектора
. Числа х, у, z называются координатами вектора  в данной декартовой системе координат.
в данной декартовой системе координат.
 Определение: Декартова система координат в пространстве называется прямоугольной, если базисные векторы попарно взаимно перпендикулярны и единичны.
Определение: Декартова система координат в пространстве называется прямоугольной, если базисные векторы попарно взаимно перпендикулярны и единичны.
 – прямоугольная декартова система координат в пространстве.
– прямоугольная декартова система координат в пространстве.
 .
.
О – начало координат;
Ох – ось абсцисс;
Оу – ось ординат;
Оz – ось аппликат.
Замечание: 1. Базисные векторы  в прямоугольной декартовой системе координат называются ортами.
в прямоугольной декартовой системе координат называются ортами.
 2. Любой вектор
2. Любой вектор  может быть единственным образом разложен по ортам
может быть единственным образом разложен по ортам  :
:  . Числа х, у, z являются координатами вектора
. Числа х, у, z являются координатами вектора  в данной прямоугольной декартовой системе координат.
в данной прямоугольной декартовой системе координат.
Пример:
Дано: ABCDA1B1C1D1 – куб.
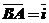 ;
;  ;
;  .
.
M – середина AD;
H – середина DC;
F – середина AA1;
N – середина A1 B1;
K – середина B1 C1;
L – середина D1 C1;
P – середина C1 C.
Разложить векторы  по векторам
по векторам  .
.
Решение:
Воспользуемся «правилом многоугольника» сложения нескольких векторов:
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
Упражнения:
1. Дан куб ABCDA1B1C1D1. Являются ли компланарными следующие векторы:
а)  г)
г) 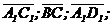
б)  д)
д) 
в)  е)
е) 
2. В кубе ABCDA1B1C1D1 за базис взяты векторы  ;
; 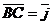 ;
;  ;
;
M – середина A1 B1; N – середина B1 C1; S – середина BC; Q – середина AD;
R – середина CD; T – середина BB1; P – середина AB. Разложить по базису  векторы
векторы  .
.
5. Построение точек плоскости (пространства), заданных координатами
Пример:
Построить в 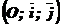 точки
точки
А(2; - 3);
В (- 1; 4);
С (- 3; - 2);
D(0; - 1).
 Пример: Построить в
Пример: Построить в  точки
точки
А(2; 3; 4);
В (- 1; - 3; 3);
С (0; 4; 2);
D(0; 0; 5);
Е(- 2; 0; 6).
6. Понятие радиус-вектора точки. Разложение радиус-вектора точки по ортам
Определение; Радиус-вектором точки называется вектор, начало которого совпадает с началом координат, а конец с данной точкой.
Вывод:
1. Каждой точке плоскости (пространства) соответствует свой радиус-вектор.
Рис. 1. Рис. 2.
Рис. 1.
В  точка М (х; у) имеет радиус-вектор
точка М (х; у) имеет радиус-вектор  .
.
Рис. 2.
В  точка М (х; у; z) имеет радиус-вектор
точка М (х; у; z) имеет радиус-вектор  .
.
Упражнения:
1. Определить координаты орт в  и
и  .
.
2. Построить радиус-векторы точек А (2; - 1; 4); В (- 3; 2; - 5); С (0; 0; 4).
3. Разложить радиус-векторы точек А (- 1; 4; 0); В (2; - 2; 5); С (0; 3; - 2) по ортам.
4. Определить координаты радиус-векторов точек М, К, L, E, H если:
 .
.
7. Определение координат вектора на плоскости и в пространстве
Задача: Определить координаты 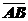 в
в  ,
,
если А (х1; у1) и В (х2; у2).
Дано:
 ;
;
А (х1; у1);
В (х2; у2).
Определить:
 .
.
Решение:
Построим радиус-векторы 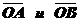 точек А и В.
точек А и В.
А (х1; у1)  - разложение
- разложение 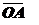 по ортам;
по ортам;
В (х2; у2)  - разложение
- разложение  по ортам;
по ортам;
По правилу вычитания двух векторов 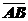 можно представить в виде разности
можно представить в виде разности 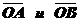 .
.

 - разложение
- разложение 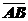 по ортам, где х = х2 - х1; у = у2 - у1.
по ортам, где х = х2 - х1; у = у2 - у1.

Вывод: Разложить вектор по ортам, значит представить его в виде суммы произведений координат вектора на соответствующие орты.

 .
. 
 .
.
Правило: Чтобы определить координаты любого вектора, надо из координат конца этого вектора вычесть одноименные координаты его начала.
 .
.
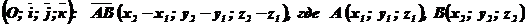 .
.
Пример: Определить координаты 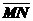 , если М (- 3; 0; 4) и N (1; - 5; - 3).
, если М (- 3; 0; 4) и N (1; - 5; - 3).
 Дано: Решение:
Дано: Решение:
 Воспользуемся правилом определения координат вектора:
Воспользуемся правилом определения координат вектора:
С (- 4; - 5); начала.
D (5; - 2).  ;
; 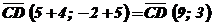 .
.
Тема: «Векторы на плоскости и в пространстве»
- Понятие вектора
Векторы находят широкое применение в математике, физике, механике и других дисциплинах, упрощают вывод многих формул, решение многих задач, доказательство теорем.
Слово «вектор» происходит от латинского слова «vector» - переноситель, несущий.
 Рассмотрим упорядоченную пару несовпадающих точек (А;В). Соединим точку А с точкой В и укажем направление от А к В. С помощью этой пары зададим преобразование плоскости (пространства). Каждой точке М плоскости (пространства) поставим в соответствие точку М1 плоскости (пространства) (ее образ), которая получится в результате следующего построения: приняв точку М за начало, проводим луч т, одинаково направленный с лучом АВ. На луче т имеется единственная точка М1, удаленная от точки М на расстояние, равное АВ.
Рассмотрим упорядоченную пару несовпадающих точек (А;В). Соединим точку А с точкой В и укажем направление от А к В. С помощью этой пары зададим преобразование плоскости (пространства). Каждой точке М плоскости (пространства) поставим в соответствие точку М1 плоскости (пространства) (ее образ), которая получится в результате следующего построения: приняв точку М за начало, проводим луч т, одинаково направленный с лучом АВ. На луче т имеется единственная точка М1, удаленная от точки М на расстояние, равное АВ.
Такое преобразование плоскости (пространства), определяемое упорядоченной парой точек называется «параллельным переносом» или «вектором».
Определение: Вектором или параллельным переносом, определяемым упорядоченной парой точек (А;В), называется преобразование плоскости (пространства), при котором каждая точка М плоскости (пространства)отображается на точку М1 плоскости (пространства) так, что луч ММ1 одинаково направлен с лучом АВ и расстояние ММ1 равно расстоянию АВ.
Определение: Нулевым вектором называется вектор, начало которого совпадает с его концом.  – нулевой вектор.
– нулевой вектор.
Вывод:
- Любой ненулевой вектор задается упорядоченной парой несовпадающих точек.
-
 Любой ненулевой вектор изображается направленным отрезком.
Любой ненулевой вектор изображается направленным отрезком.
Обозначение: 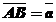
А – начало вектора 
В – конец вектора 
Определение: Направлением ненулевого вектора  называется направление луча АВ.
называется направление луча АВ.
Определение: Длиной вектора  (абсолютной величиной, модулем) называется расстояние между его началом и концом.
(абсолютной величиной, модулем) называется расстояние между его началом и концом.
Определение: Вектор, длина которого равна единице, называется единичным вектором.
Вывод:
- Любой ненулевой вектор характеризуется направлением и абсолютной величиной.
- Длина нулевого вектора равна нулю, понятие направления не определено.

Определение: Два вектора называются одинаково направленными, если они имеют одинаковые направления. (Рис. 1)
Определение: Два вектора называются равными, если они имеют одинаковые направления и длины. (Рис. 3)
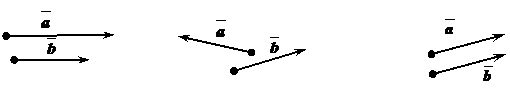 Рис. 1. Рис. 2. Рис. 3.
Рис. 1. Рис. 2. Рис. 3.


 Û
Û  и
и 
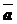 и
и 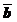
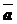 и
и 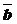
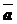 и
и 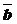
одинаково направленные векторы равные векторы



 Рассмотрим упорядоченную пару несовпадающих точек (А;В). Соединим точку А с точкой В и укажем направление от А к В. С помощью этой пары зададим преобразование плоскости (пространства). Каждой точке М плоскости (пространства) поставим в соответствие точку М1 плоскости (пространства) (ее образ), которая получится в результате следующего построения: приняв точку М за начало, проводим луч т, одинаково направленный с лучом АВ. На луче т имеется единственная точка М1, удаленная от точки М на расстояние, равное АВ.
Рассмотрим упорядоченную пару несовпадающих точек (А;В). Соединим точку А с точкой В и укажем направление от А к В. С помощью этой пары зададим преобразование плоскости (пространства). Каждой точке М плоскости (пространства) поставим в соответствие точку М1 плоскости (пространства) (ее образ), которая получится в результате следующего построения: приняв точку М за начало, проводим луч т, одинаково направленный с лучом АВ. На луче т имеется единственная точка М1, удаленная от точки М на расстояние, равное АВ. – нулевой вектор.
– нулевой вектор. Любой ненулевой вектор изображается направленным отрезком.
Любой ненулевой вектор изображается направленным отрезком. 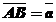

 называется направление луча АВ.
называется направление луча АВ.
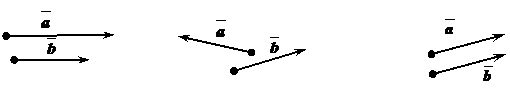 Рис. 1. Рис. 2. Рис. 3.
Рис. 1. Рис. 2. Рис. 3.

 Û
Û  и
и 
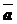 и
и 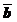
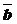
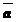 и
и 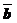 противоположные векторы, то пишут
противоположные векторы, то пишут 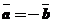 или
или 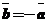 .
.
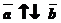
 и
и 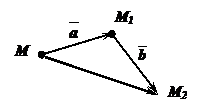 Сложение векторов.
Сложение векторов.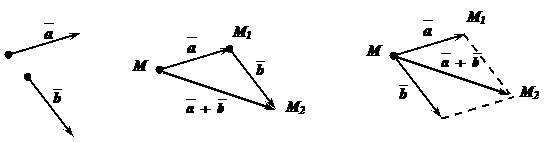 Определение: Суммой
Определение: Суммой 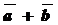 векторов
векторов 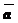 и
и 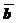 называется композиция этих векторов.
называется композиция этих векторов.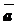 и
и 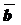 по «правилу треугольника», надо от произвольной точки плоскости отложить
по «правилу треугольника», надо от произвольной точки плоскости отложить 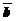 будет вектор
будет вектор 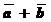 , начало которого совпадет с началом
, начало которого совпадет с началом 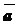 и
и 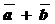 , изображаемый диагональю параллелограмма, идущей из их общего начала. (Рис. 2.)
, изображаемый диагональю параллелограмма, идущей из их общего начала. (Рис. 2.)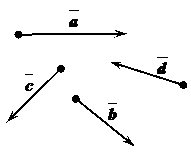 Пример:
Пример: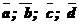
 Построить:
Построить: 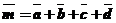
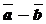 двух векторов
двух векторов 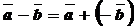
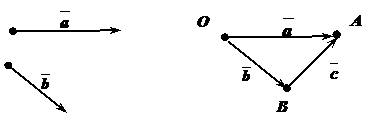
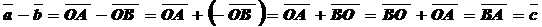
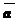 на число х, неравное нулю, называется вектор
на число х, неравное нулю, называется вектор 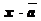 , длина которого равна
, длина которого равна 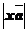 , а направление совпадает с направлением
, а направление совпадает с направлением 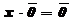 ;
; 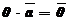 .
. 
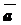 ; х1 = - 2; х2 = 3; х3 =
; х1 = - 2; х2 = 3; х3 = 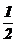 .
.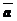 ; 3
; 3 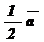 .
.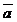 и
и 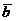 построить следующие векторы:
построить следующие векторы: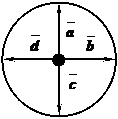

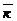 ,
, 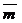 и
и 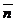 построить следующие векторы:
построить следующие векторы: 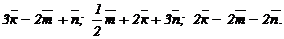
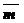 может быть единственным образом разложен по базисным векторам
может быть единственным образом разложен по базисным векторам  и
и  :
: 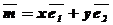 . Числа х и у называются координатами вектора
. Числа х и у называются координатами вектора  Определение: Декартова система координат на плоскости называется прямоугольной, если базисные векторы взаимно перпендикулярны и единичны.
Определение: Декартова система координат на плоскости называется прямоугольной, если базисные векторы взаимно перпендикулярны и единичны.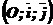 – прямоугольная декартова система координат на плоскости.
– прямоугольная декартова система координат на плоскости. .
. в прямоугольной декартовой системе координат называются ортами.
в прямоугольной декартовой системе координат называются ортами. . Числа х и у являются координатами вектора
. Числа х и у являются координатами вектора  и
и  коллинеарны.
коллинеарны. 2. В прямоугольнике АВСD проведены диагонали АС и ВD, пересекающиеся в точке О.
2. В прямоугольнике АВСD проведены диагонали АС и ВD, пересекающиеся в точке О. 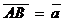 ,
,  . Выразить через
. Выразить через 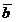 следующие векторы:
следующие векторы: 
 компланарны, а векторы
компланарны, а векторы  компланарными не являются.
компланарными не являются.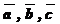 , то любой вектор
, то любой вектор  можно разложить по векторам
можно разложить по векторам 
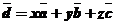 - существует;
- существует; может быть единственным образом разложен по базисным векторам
может быть единственным образом разложен по базисным векторам  :
:  . Числа х, у, z называются координатами вектора
. Числа х, у, z называются координатами вектора  Определение: Декартова система координат в пространстве называется прямоугольной, если базисные векторы попарно взаимно перпендикулярны и единичны.
Определение: Декартова система координат в пространстве называется прямоугольной, если базисные векторы попарно взаимно перпендикулярны и единичны. – прямоугольная декартова система координат в пространстве.
– прямоугольная декартова система координат в пространстве. .
. в прямоугольной декартовой системе координат называются ортами.
в прямоугольной декартовой системе координат называются ортами. 2. Любой вектор
2. Любой вектор  :
:  . Числа х, у, z являются координатами вектора
. Числа х, у, z являются координатами вектора 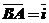 ;
;  ;
;  .
. по векторам
по векторам  ;
; ;
; ;
; ;
; .
. г)
г) 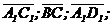
 д)
д) 
 е)
е) 
 ;
; 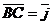 ;
;  ;
; векторы
векторы  .
.
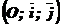 точки
точки Пример: Построить в
Пример: Построить в  точки
точки точка М (х; у) имеет радиус-вектор
точка М (х; у) имеет радиус-вектор  .
. .
. и
и  .
. .
.
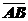 в
в  .
.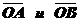 точек А и В.
точек А и В. - разложение
- разложение 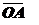 по ортам;
по ортам; - разложение
- разложение  по ортам;
по ортам;
 - разложение
- разложение 
 .
.  .
. .
.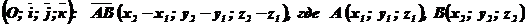 .
.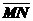 , если М (- 3; 0; 4) и N (1; - 5; - 3).
, если М (- 3; 0; 4) и N (1; - 5; - 3). Дано: Решение:
Дано: Решение: ;
; 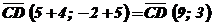 .
.

