

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров...
История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
Интересное:
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Принципы управления денежными потоками: одним из методов контроля за состоянием денежной наличности является...
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Гиперболические функции встречаются в механике, электротехнике и других технических дисциплинах. Многие формулы для гиперболических функций похожи на формулы для тригонометрических функций, кроме свойства ограниченности.
| № | Функция 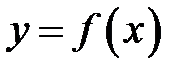
| Название | Производная 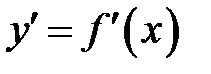
|
| 1. | 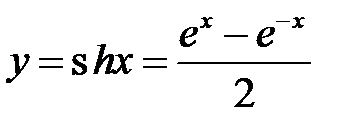
| гиперболический синус | 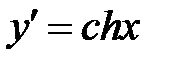
|
| 2. | 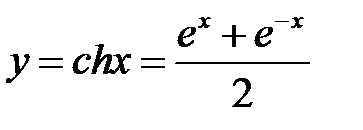
| гиперболический косинус | 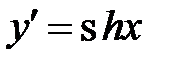
|
| 3. | 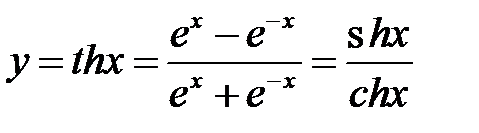
| гиперболический тангенс | 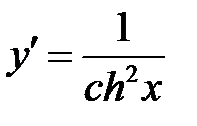
|
| 4. | 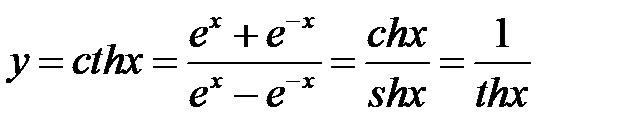
| гиперболический котангенс | 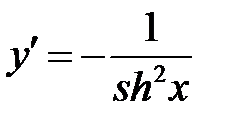
|
Формулы для гиперболических функций
1. 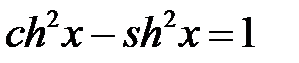 .
.
Доказательство. Рассмотрим искомую разность
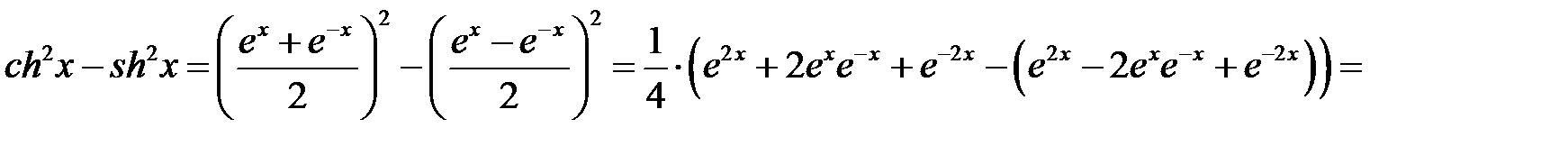
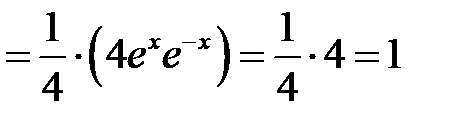 . Соединяя начало и конец, получим доказываемое равенство:
. Соединяя начало и конец, получим доказываемое равенство: 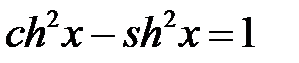 .
.
2. 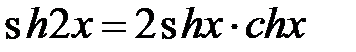 .
.
Доказательство. Рассмотрим произведение
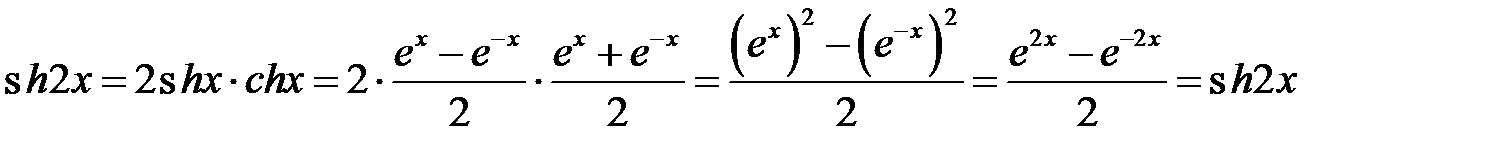 . Соединяя начало и конец, получим доказываемое равенство:
. Соединяя начало и конец, получим доказываемое равенство: 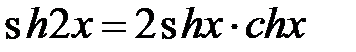 .
.
3. 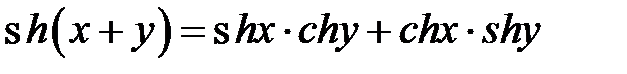 .
.
Доказательство. Рассмотрим произведение 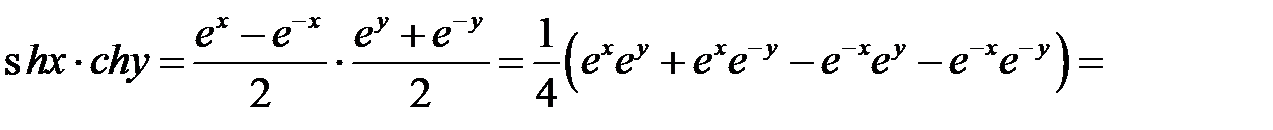
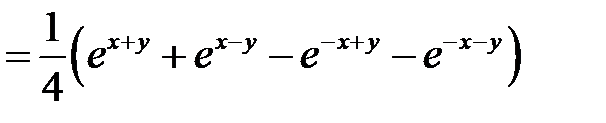 .
.
Рассмотрим произведение 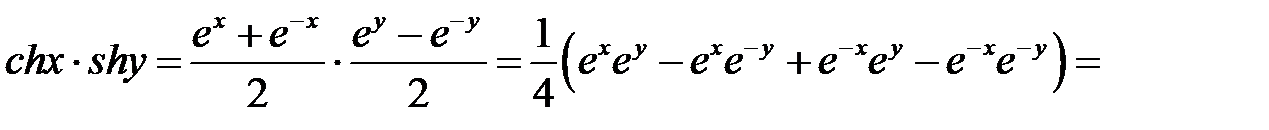
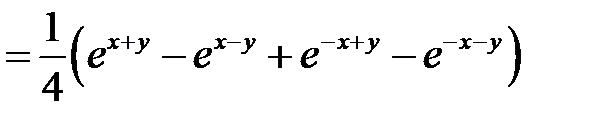 .
.
Сложим два произведения и приведем подобные:
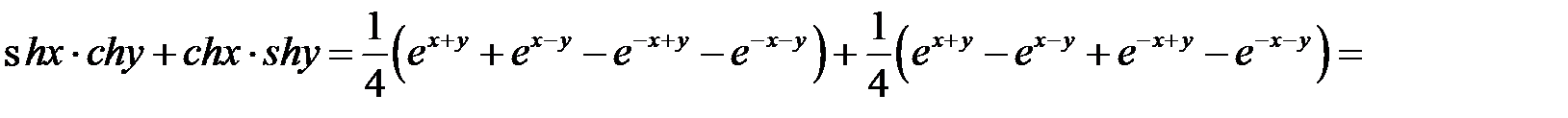
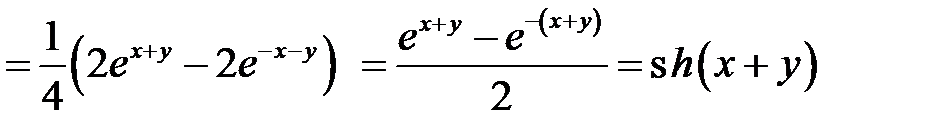 . Соединяя начало и конец, получим доказываемое равенство:
. Соединяя начало и конец, получим доказываемое равенство: 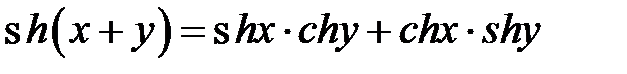 .
.
Ещё много других свойств гиперболических функций похожих на свойства тригонометрических функций, которые доказываются аналогично.
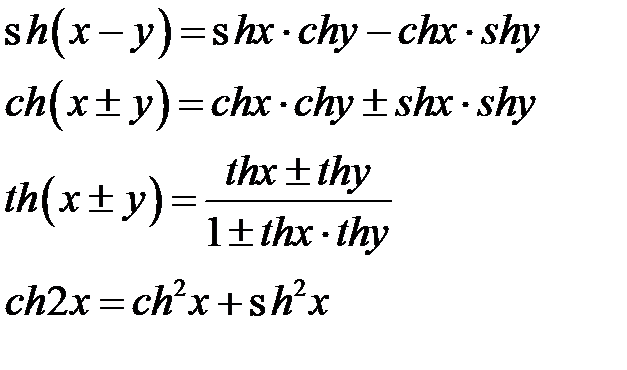
Докажем формулы для производных гиперболических функций.
1. Рассмотрим гиперболический синус 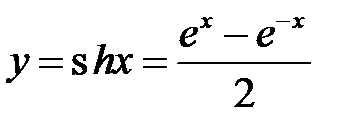 .
.
При нахождении производной константу  выносим за знак производной. Далее применяем свойство о производной разности двух функций
выносим за знак производной. Далее применяем свойство о производной разности двух функций 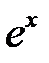 и
и 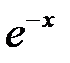 . Находим производную функции
. Находим производную функции 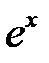 по таблице производных:
по таблице производных: 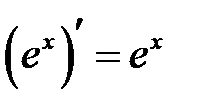 . Производную функции
. Производную функции 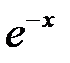 ищем как производную сложной функции
ищем как производную сложной функции 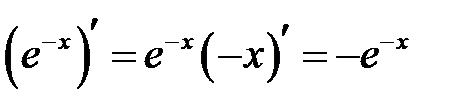 .
.
Поэтому, производная 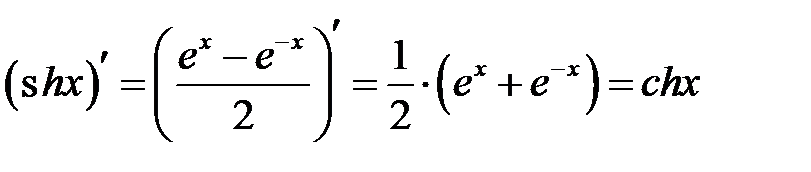 .
.
Соединяя начало и конец, получим доказываемое равенство: 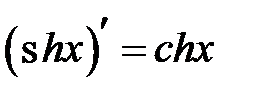 .
.
2. Рассмотрим гиперболический косинус 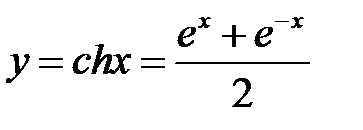 .
.
Полностью применяем предыдущий алгоритм, только вместо свойства о производной разности двух функций 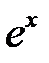 и
и 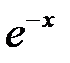 применяем свойство о производной суммы двух этих функций.
применяем свойство о производной суммы двух этих функций. 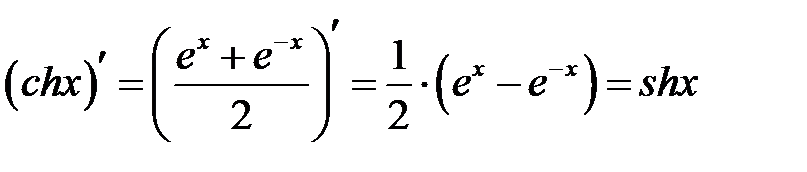 .
.
|
|
Соединяя начало и конец, получим доказываемое равенство: 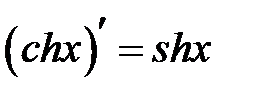 .
.
3. Рассмотрим гиперболический тангенс 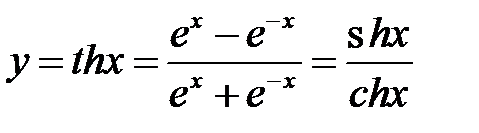 .
.
Находим производную по правилу отыскания производной дроби.
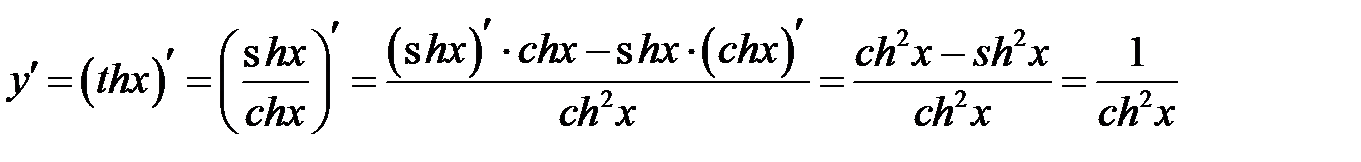 .
.
4. Производную гиперболического котангенса
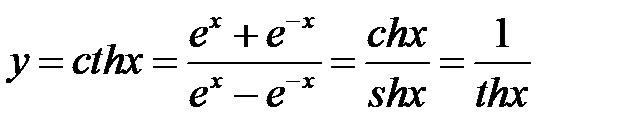 можно найти как производную сложной функции
можно найти как производную сложной функции 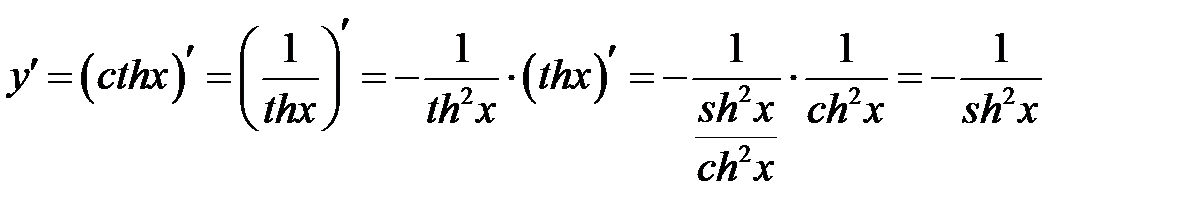 .
.
Соединяя начало и конец, получим доказываемое равенство: 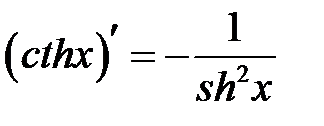 .
.
Дифференциал функции
Пусть функция 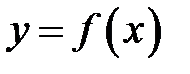 – дифференцируема в точке
– дифференцируема в точке 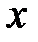 , тогда её приращение
, тогда её приращение 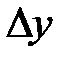 этой функции в точке
этой функции в точке 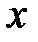 , соответствующее приращению аргумента
, соответствующее приращению аргумента 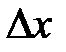 , может быть представлено в виде
, может быть представлено в виде
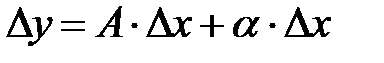 , (8.1)
, (8.1)
где 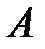 – некоторое число, не зависящее от
– некоторое число, не зависящее от 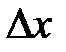 , а
, а 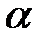 – функция аргумента
– функция аргумента 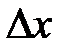 , которая является бесконечно малой при
, которая является бесконечно малой при 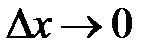 .
.
Таким образом, приращение 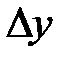 функции
функции 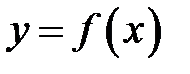 представляет собой сумму двух бесконечно малых слагаемых
представляет собой сумму двух бесконечно малых слагаемых 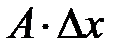 и
и 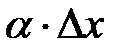 . Было показано, что второе слагаемое
. Было показано, что второе слагаемое 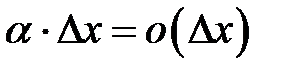 является бесконечно малой функцией более высокого порядка, чем т.е.
является бесконечно малой функцией более высокого порядка, чем т.е. 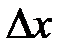 (см. 8.1). Поэтому первое слагаемое
(см. 8.1). Поэтому первое слагаемое 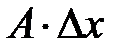 является главной линейной частью приращения
является главной линейной частью приращения 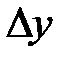 функции
функции 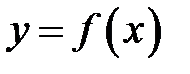 . В замечании 8.1. получена другая формула (8.1.1) для приращения
. В замечании 8.1. получена другая формула (8.1.1) для приращения 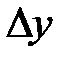 функции
функции 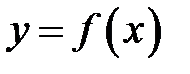 , а именно:
, а именно: 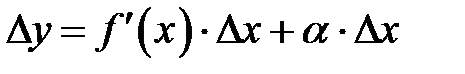 . (8.1.1)
. (8.1.1)
Определение 8.3.Дифференциалом функции 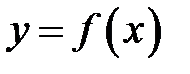 в точке
в точке 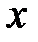 называется главная линейная частью её приращения, равная произведению производной
называется главная линейная частью её приращения, равная произведению производной 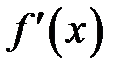 в этой точке
в этой точке 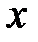 на произвольное приращение
на произвольное приращение 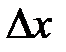 аргумента
аргумента 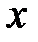 , и обозначается
, и обозначается 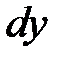 (или
(или 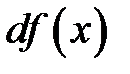 ):
):
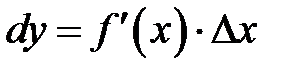 (8.4)
(8.4)
Дифференциал 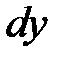 функции
функции 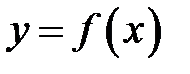 называют также дифференциалом первого порядка.
называют также дифференциалом первого порядка.
Под дифференциалом 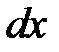 независимой переменной
независимой переменной 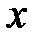 понимается любое, независящее от
понимается любое, независящее от 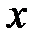 , число. Чаще всего, в качестве этого числа берётся приращение переменной
, число. Чаще всего, в качестве этого числа берётся приращение переменной 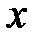 , т.е.
, т.е. 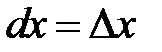 . Это согласуется с правилом(8.4) нахождения дифференциала функции
. Это согласуется с правилом(8.4) нахождения дифференциала функции 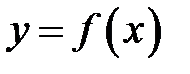
Рассмотрим функцию 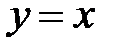 и найдем её дифференциал.
и найдем её дифференциал.
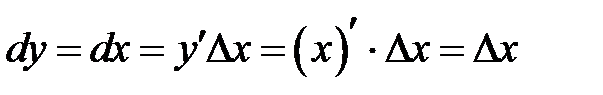 , т.к. производная
, т.к. производная 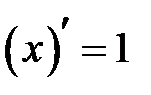 . Таким образом, получили:
. Таким образом, получили: 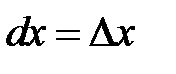 и дифференциал
и дифференциал 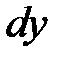 функции
функции 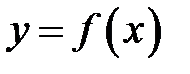 можно находить по формуле
можно находить по формуле
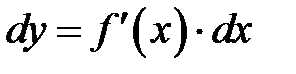 . (8.4.1)
. (8.4.1)
Замечание 8.7. Из формулу (8.4.1) следует, что. 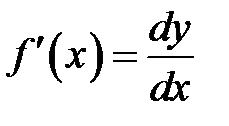
Таким образом, запись 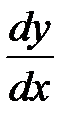 можно понимать не только как обозначение для производной
можно понимать не только как обозначение для производной 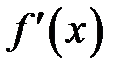 , но и как отношение дифференциалов зависимого и независимого переменных.
, но и как отношение дифференциалов зависимого и независимого переменных.
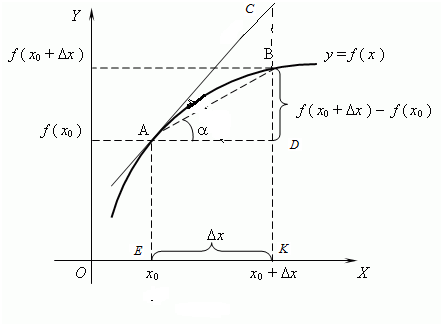
8.7. Геометрический смысл дифференциала функции
Пусть к графику функции 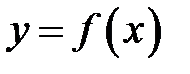 проведена (см. рис. 8.1) касательная
проведена (см. рис. 8.1) касательная 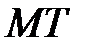 . Точка
. Точка 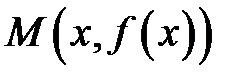 находится на графике функции
находится на графике функции 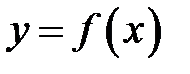 и имеет абсциссу –
и имеет абсциссу – 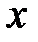 . Даем
. Даем 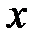 произвольное приращение
произвольное приращение 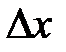 , такое, чтобы точка
, такое, чтобы точка 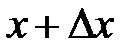 не вышла из области определения функции
не вышла из области определения функции 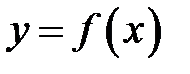 .
.
|
|
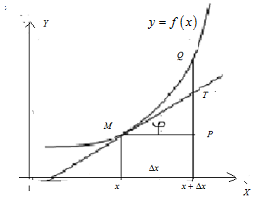
Рисунок 8.1 Изображение графика функции
Точка 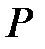 имеет координаты
имеет координаты 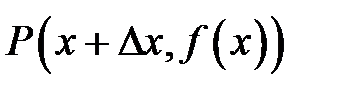 . Отрезок
. Отрезок 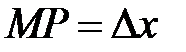 . Точка
. Точка 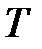 лежит на касательной к графику функции
лежит на касательной к графику функции 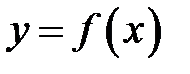 и имеет абсциссу –
и имеет абсциссу – 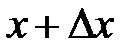 . Из прямоугольного
. Из прямоугольного  следует, что
следует, что 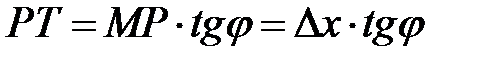 , где угол
, где угол 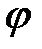 – угол между положительным направлением оси
– угол между положительным направлением оси 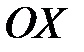 и касательной, проведенной к графику функции
и касательной, проведенной к графику функции 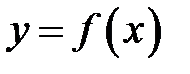 в точке
в точке 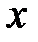 . По определению дифференциала
. По определению дифференциала 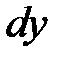 функции
функции 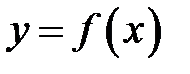 и геометрического смысла производной функции
и геометрического смысла производной функции 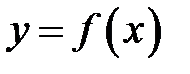 в точке
в точке 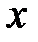 , делаем вывод, что
, делаем вывод, что 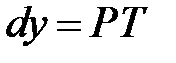 . Таким образом, геометрический смысл дифференциала функции
. Таким образом, геометрический смысл дифференциала функции 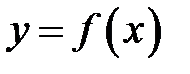 заключается в том, что дифференциал
заключается в том, что дифференциал 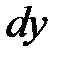 представляет собойприращение ординаты касательной к графику функции
представляет собойприращение ординаты касательной к графику функции 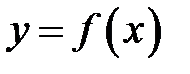 в точке
в точке 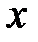 .
.
Замечание 8.8. Дифференциал 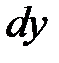 и приращение
и приращение 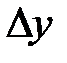 для произвольной функции
для произвольной функции 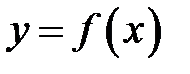 , вообще говоря, не равны между собой.В общем случае, разность между приращением и дифференциалом функции является бесконечно малой высшего порядка малости, чем приращение аргумента. Из определения 8.1следует, что
, вообще говоря, не равны между собой.В общем случае, разность между приращением и дифференциалом функции является бесконечно малой высшего порядка малости, чем приращение аргумента. Из определения 8.1следует, что 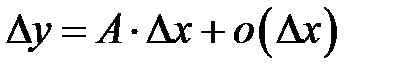 , т.е.
, т.е. 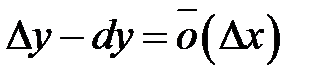 .
.
На рисунке 8.1точка  лежит на графике функции
лежит на графике функции 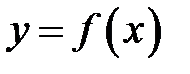 и имеет координаты
и имеет координаты 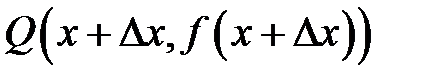 . Отрезок
. Отрезок 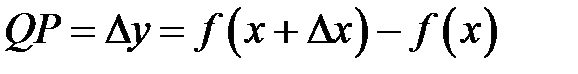 .
.
На рисунке 8.1 выполнено неравенство 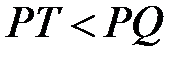 , т.е.
, т.е. 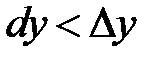 . Но возможны случаи, когда справедливо противоположное неравенство
. Но возможны случаи, когда справедливо противоположное неравенство 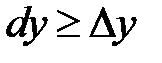 . Это выполняется для линейной функции и для выпуклой вверх функции.
. Это выполняется для линейной функции и для выпуклой вверх функции.
|
|
|

Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ - конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!