Определение. Последовательность  называется бесконечные малой, если для любого положительного числа ε можно указать номер N такой, что при
называется бесконечные малой, если для любого положительного числа ε можно указать номер N такой, что при 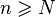 все элементы
все элементы 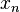 этой последовательности удовлетворяют неравенству
этой последовательности удовлетворяют неравенству 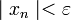 .
.
Любая бесконечно малая последовательность является ограниченной.
Определение. Бесконечно малая последовательность — это последовательность, предел которой равен 0. То есть, если  . Например, последовательность чисел
. Например, последовательность чисел 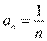 — бесконечно малая.
— бесконечно малая.
Определение. Последовательность  называется бесконечно большой, если для любого положительного числа A можно указать номер N такой, что при
называется бесконечно большой, если для любого положительного числа A можно указать номер N такой, что при 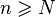 все элементы
все элементы 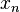 этой последовательности удовлетворяют неравенству
этой последовательности удовлетворяют неравенству  .
.
Любая бесконечно большая последовательность является неограниченной. Но не каждая неограниченная последовательность является бесконечно большой. Например, неограниченная последовательность 1, 2, 1, 3,... 1, n,... не является бесконечно большой, так как при A > 1 неравенство  не выполняется для
не выполняется для 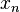 с нечетными номерами
с нечетными номерами
- Бесконечно большая последовательность — это последовательность, предел которой равен бесконечности.
Пример 21. Последовательности n, 2 n являются бесконечно большими.
Следует различать неограниченную и бесконечно большую последовательности. Всякая бесконечно большая последовательность является неограниченной, однако неограниченная не обязательно является бесконечно большой. Рассмотрим следующий пример.
Пример 22. Пусть xn = 1,1/2,3,1/3,5,1/4,..., нетрудно заметить, что данная последовательность состоит из двух составляющих, а именно x2k-1 = 2k-1, x2k = 1/(k+1). Данная последовательность неограниченная, так как содержит неограниченную составляющую x2k-1 = 2k-1, но не является бесконечно большой, так как содержит вторую часть x2k = 1/(k+1).
Пример 22. Пусть xn = 1,1/2,3,1/3,5,1/4,..., нетрудно заметить, что данная последовательность состоит из двух составляющих, а именно x2k-1 = 2k-1, x2k = 1/(k+1). Данная последовательность неограниченная, так как содержит неограниченную составляющую x2k-1 = 2k-1, но не является бесконечно большой, так как содержит вторую часть x2k = 1/(k+1).
Очевидно следующее утверждение.
Лемма 1. Если n — бесконечно малая последовательность, то 1 / n —бесконечно большая последовательность.
Пример 23. Пусть n = 1/n, которая является бесконечно малой, тогда последовательность n = 1/ n = n будет бесконечно большой.
Теорема 5. Для того чтобы последовательность { xn } имела предел, равный A необходимо и достаточно, чтобы ее члены имели вид
xn = A+ n,
где
lim n n = 0.
Справедливы следующие свойства бесконечно малых последовательностей, которые легко получить из определения бесконечно малой последовательности.
Теорема 6. (свойства бесконечно малых последовательностей)
Бесконечно малые последовательности имеют следующие свойства.
1. Сумма и разность бесконечно малых последовательностей есть также бесконечно малая последовательность.
2. Бесконечно малая последовательность ограничена.
3. Произведение бесконечно малой последовательности на ограниченную последовательность есть бесконечно малая последовательность.
4. Если { xn } – бесконечно большая последовательность, то, начиная с некоторого N, определена последовательность {1/ xn }, и она есть бесконечно малая последовательность. Наоборот, если { xn } – бесконечно малая последовательность и все xn отличны от нуля, то {1/ xn } есть бесконечно большая последовательность
1..
Следствие 1. Произведение конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.
Алгебраическая сумма конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.
Теорема 5. предел последовательности  равен
равен 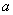 тогда, и только тогда, когда
тогда, и только тогда, когда  представимо в виде суммы
представимо в виде суммы  , где
, где 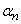 - бесконечно малая.
- бесконечно малая.
Теорема 8. Сходящаяся числовая последовательность ограничена.
Доказательство. Пусть  – сходящаяся к числу а, тогда
– сходящаяся к числу а, тогда  , где
, где  . Так как бесконечно малая последовательность ограничена, то $ такое число
. Так как бесконечно малая последовательность ограничена, то $ такое число 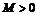 , что для всех
, что для всех  выполняется
выполняется 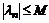 . Поэтому
. Поэтому  для всех
для всех  , а это и означает, что последовательность
, а это и означает, что последовательность  ограничена.
ограничена.
Рассмотренные последовательности 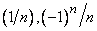 являются бесконечно малыми. Последовательность
являются бесконечно малыми. Последовательность  , как следует из (2), отличается от 1 на бесконечно малую
, как следует из (2), отличается от 1 на бесконечно малую  , и потому предел этой последовательности равен
, и потому предел этой последовательности равен



 называется бесконечные малой, если для любого положительного числа ε можно указать номер N такой, что при
называется бесконечные малой, если для любого положительного числа ε можно указать номер N такой, что при 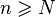 все элементы
все элементы 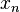 этой последовательности удовлетворяют неравенству
этой последовательности удовлетворяют неравенству 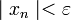 .
. . Например, последовательность чисел
. Например, последовательность чисел 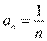 — бесконечно малая.
— бесконечно малая. .
. равен
равен 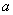 тогда, и только тогда, когда
тогда, и только тогда, когда  представимо в виде суммы
представимо в виде суммы  , где
, где 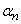 - бесконечно малая.
- бесконечно малая. – сходящаяся к числу а, тогда
– сходящаяся к числу а, тогда  , где
, где  . Так как бесконечно малая последовательность ограничена, то $ такое число
. Так как бесконечно малая последовательность ограничена, то $ такое число 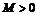 , что для всех
, что для всех  выполняется
выполняется 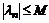 . Поэтому
. Поэтому  для всех
для всех 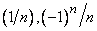 являются бесконечно малыми. Последовательность
являются бесконечно малыми. Последовательность  , как следует из (2), отличается от 1 на бесконечно малую
, как следует из (2), отличается от 1 на бесконечно малую  , и потому предел этой последовательности равен
, и потому предел этой последовательности равен


