Система функций будет полной если она содержит хотя бы одну из функций:
- несамодвойственную
- несохраняющую 0
- несохраняющую 1
- немонотонную
- нелинейную
Доказательство:
Доказательство теоремы сводится к доказательству утверждения: имеет несамодвойственную, несохраняющую 0 и 1 функции можно получить конст-ты 0 или 1. Если тезис будет доказан, то теорема сводится к первой теореме о функциональной полноте.
Начнем доказательство с того, что покажем как с помощью несамодвойственной функции получить конст-ту, если имеется конст-та х и 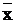 . Допустим, что имеется несамодвойственная функция f от n аргументов, тогда для нее можно найти такой набор d, чтобы выполнялось равенство:
. Допустим, что имеется несамодвойственная функция f от n аргументов, тогда для нее можно найти такой набор d, чтобы выполнялось равенство:
f (d1, d2, …, dn) = 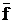 (
( 1,
1,  2, …,
2, …,  n)
n)
Определим функцию f (x)
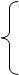 f (x) = f (xd1, xd2, …, xdn), где
f (x) = f (xd1, xd2, …, xdn), где
x, di = 1
xdi =
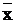 , di = 0, при этом
, di = 0, при этом
0di =  i, 1di =
i, 1di =  i, тогда
i, тогда
f (0) = f (0d1, 0d2, …, 0dn) = f ( 1,…,
1,…,  n) = f (d1, …, dn) = f (1d1, …, 1dn) = f (1)
n) = f (d1, …, dn) = f (1d1, …, 1dn) = f (1)
т.е. f (x) = const.
Рассмотрим 2 случая для функции несохраняющей 0:
1. Имеем функцию несохраняющую 0 следующего вида:
f0 (x1, …, xn)
d0 (0) = f0 (0, …, 0) = 1
d0 (1) = f0 (1, …, 1) = 0 Þ d0 (x) = 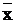
А если есть х и 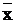 , то подставив их в несамодвойственную функцию получим коснтанту, если понадобится противоположная конст-та, то ее можно получить отрицанием.
, то подставив их в несамодвойственную функцию получим коснтанту, если понадобится противоположная конст-та, то ее можно получить отрицанием.
2. Имеем функцию несохраняющую 0 вида:
f0 (x1, …, xn)
d0 (0) = f0 (0, …, 0) = 1
d0 (1) = f0 (1, …, 1) = 1 Þ d0 (x) = 1
Имеем конст-ту 1.
Для получения конст-ты 0 используем функцию несохраняющую 1 вида:
f1 (x1, …, xn)
d1 (1) = f1 (1, …, 1) = Æ Þ d1 (d0 (x)) = Æ
т.е. получена конст-та 0.
Таким образом доказана достаточность теоремы.
Доказательство необходимости теоремы следует из замкнутости классов самодвойственных, сохраняющих 0 и 1 функций.
Таким образом теорема доказана.
На основании 2-й теоремы о функциональной полноте, построим расширенную таблицу Поста:
| yi
| Kн
| Кл
| K0
| K1
| Kc
|
|
| f1
|
|
|
|
|
| a
|
| f2
|
|
|
|
|
| b
|
| f6
|
|
|
|
|
| c
|
| f7
|
|
|
|
|
| d
|
| f8
|
|
|
|
|
| e
|
| f9
|
|
|
|
|
| f
|
| F12
|
|
|
|
|
| g
|
| F13
|
|
|
|
|
| h
|
| F14
|
|
|
|
|
| k
|
| х1
| х2
| F1
| F2
| F6
| F7
| F8
| F9
| F12
| F13
| F14
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| F1 = х1*х2
|
F2 = х1* 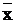 2 = х1х2 Å x1 2 = х1х2 Å x1
|
F6 = 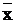 1*х2 + х1* 1*х2 + х1* 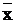 2 = х1Åх2 2 = х1Åх2
|
| F7 = х1 + х2 = х1х2 Å x1 Å х2
|
F8 = 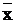 1* 1* 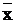 2 = х1х2 Å x1 Å х2 Å 1 2 = х1х2 Å x1 Å х2 Å 1
|
F9 = 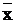 1 1 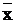 2 + х1х2 = х1Åх2 Å 1 2 + х1х2 = х1Åх2 Å 1
|
F12 = 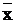 1 = х1 Å 1 1 = х1 Å 1
|
F13 = 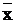 1 + х2 = х1х2 Å x1 Å 1 1 + х2 = х1х2 Å x1 Å 1
|
F14 = 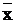 1 + 1 + 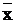 2 = х1х2 Å 1 2 = х1х2 Å 1
|
1 - не принадлежит классу.
С помощью метода Квайна найдем мин. покрытие табл., т. е. Получим все базисы в узком смысле в пр-ве Рa
P = (b + c + e + f + g + h + k)(a + b + d + e + h + k)(e + f + g + h + k) &
& (b + c + g + k)(a + b + c + d + e + f + h + k) = e + k + (b + c + f + g + h)
(a + b + d + h)(f + g + h)(b + c + g)(a + b + c + d + f + h) =
= e + k (h + b + (c + f + g)(a + d) (a + c + d + f))(f + g + h)(b + c + g) =
= e + k + (h + ac + b + a + af + ag + dc + df + dg)(g + bf + bh +c + ch) =
= e + k + hg + hb + hc + bg + bf + acf + ag + dcf + dg.
П1 = {f8} П6 = { f2 ,f12}
П2 = {f14} П7 = { f2 ,f9}
П3 = {f12 ,f13} П8 = { f1 ,f6,f9}
П4 = { f2 ,f13} П9 = { f1 ,f12}
П5 = { f6 ,f13} П10 = { f6 ,f7,f9}
П11 = {f7,f12}
Если результаты исследования базисов в узком смысле объед., то можно сделать вывод, что общее число всех возможных различных базисов равно 17.
Если сравнить базисы в узком смысле с базисами в широком смысле, то можно выявить следующие соответствия:
П1 ¾ В2
П2 ¾ В4
П9 ¾ В10
П11 ¾ В9
На основани базисов в узком смысле можно реализовать любую Булеву функцию.
Приведем Р5, его сост-т следующие функции:
{y2, y9} = П7
 y2(x1, x2) = x1
y2(x1, x2) = x1 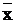 2
2
y9(x1, x2) = x1 Å x2
x1 x1
x2 & f 2 x2 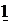 f 9
f 9
Через имеющиеся функции выразим функцию отрицания, для этого с помощью у9 получим константу 1.
y9(x, x) = 1, тогда y2(у9 (x, x) = 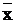
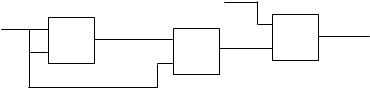
Используя функцию отрицания и y2 получим конъюкцию:
y2(x1 , y2 (у9 (x2, x2), x2)) = x1x2
 x1
x1
x2


 & x2 & x1x2
& x2 & x1x2
Имея функцию отрицания и конъюкцию, можно реализовать произвольную булеву функцию.
Если рассматривать базисы в узком и широком смысле с практической точки зрения, то следует отметить, что базисы в узком смысле не имеют никаких преимуществ, так как на практике всегда имеются константы 0 и 1.



 . Допустим, что имеется несамодвойственная функция f от n аргументов, тогда для нее можно найти такой набор d, чтобы выполнялось равенство:
. Допустим, что имеется несамодвойственная функция f от n аргументов, тогда для нее можно найти такой набор d, чтобы выполнялось равенство: (
( 1,
1,  f (x) = f (xd1, xd2, …, xdn), где
f (x) = f (xd1, xd2, …, xdn), где y2(x1, x2) = x1
y2(x1, x2) = x1 
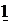 f 9
f 9 x1
x1



