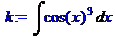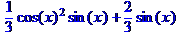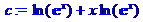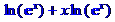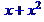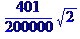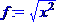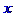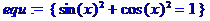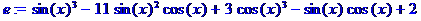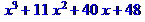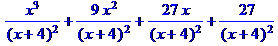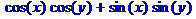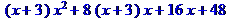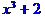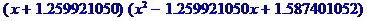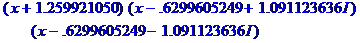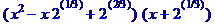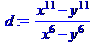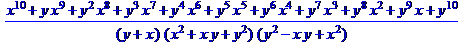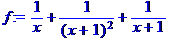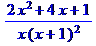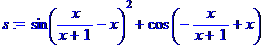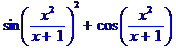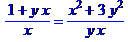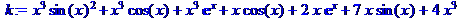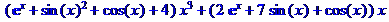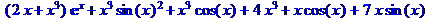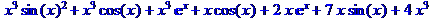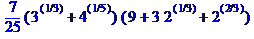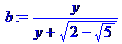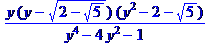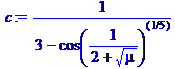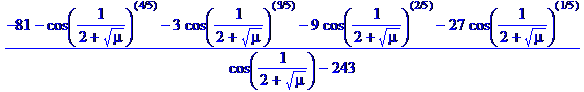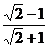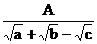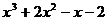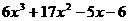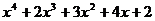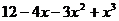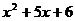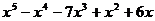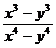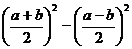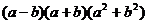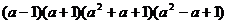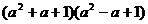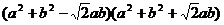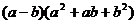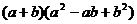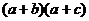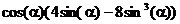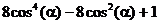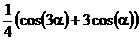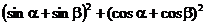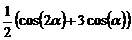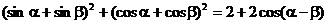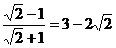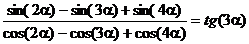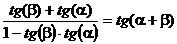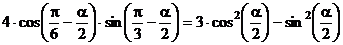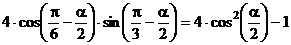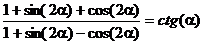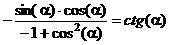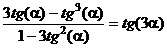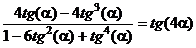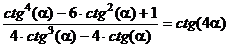Задание № 2.
ИСПОЛЬЗОВАНИЕ КОМАНД ПРЕОБРАЗОВАНИЯ ВЫРАЖЕНИЙ MAPLE ДЛЯ МАТЕМАТИЧЕСКИХ ВЫЧИСЛЕНИЙ.
Цели работы:
· знать команды, наиболее часто используемые при выполнении
аналитических вычислений;
· уметь применять указанные команды для решения математических
задач.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.
1. Команды преобразования выражений.
Процесс работы в Maple состоит в том, что пользователь создает переменные, присваивает им символьные выражения и производит над ними некоторые действия в соответствии с алгоритмом решения поставленной задачи, использую стандартные функции или написанные собственные процедуры.
Синтаксис вызова стандартной команды следующий:
команда (пар_1, пар_2,..., пар_n);
Здесь команда - это имя вызываемой функции, а пар_1, пар_2,... означают необходимые для выполнения команды параметры, которые могут быть переменными или даже выражениями, причем их тип должен соответствовать типу параметров используемой функции. Отметим, если команда завершается точкой с запятой, то результаты ее выполнения отображаются в области вывода, если команда завершается двоеточием, то она выполняется, но никакого вывода результатов не происходит.
Система обозначений функций в Maple интуитивно проста. Обычно имя функции соответствует действию, которое она выполняет (следует учесть, что все имена заданы на английском языке). Например, ясно, что функция с именем simplify () осуществляет некоторые упрощения над выражением, заданным в качестве ее параметра.
Для некоторых команд существуют активная и пассивная формы. Активная форма команды (в случае ее вызова) немедленно выполняется, а ее имя начинается со строчной буквы. Пассивная форма команды не выполняется немедленно, а просто в области вывода отображается математическая запись того, что она может сделать. Ее имя начинается с прописной буквы. В дальнейшем, если в операторе присваивания для некоторой переменной в правой части задана пассивная форма команды, то командой value () ее можно вычислить. Основное предназначение пассивных форм команд - это использование их как средства документирования производимых действий в обычной математической нотации. Примерами команд с двумя формами являются команда дифференцирования (diff и Diff), интегрирования (int и Int) и др.
Пример 1. Пассивная и активная формы команд.
> k:=Int(cos(x)^3,x);
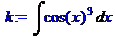
> k=int(cos(x)^3,x);

> value(k);
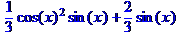
Если команды и функции являются частью ядра системы Maple, то они всегда доступны пользователю. А для вызова других команд и функций необходимо подключить библиотеку или пакет, в которых они расположены. Для этого служат команды readlib () и with (). Первая подключает библиотеку, вторая - пакет. Параметром этих команд является имя библиотеки или пакета, функции которых пользователь желает использовать.
Команды и функции Maple, наиболее часто используемые при аналитических преобразованиях, располагаются в его системном ядре – части программного обеспечения системы аналитических вычислений, постоянно находящейся в памяти компьютера. К ним относятся команды, выполняющие разнообразные преобразования выражений, получающие решение уравнений и систем уравнений, дифференцирующие функции и т. д. В данной работе вводятся команды, наиболее часто используемые при выполнении аналитических вычислений.
Пример 2. Упрощение выражений.
> c:=ln(exp(x))+x*ln(exp(x));
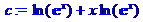
> simplify(c);
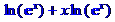
> simplify(c,assume=real);
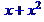
> d:=1/sqrt(8)*(((1+sqrt(8))/10)^5+((1-sqrt(8))/10)^5);

> simplify(d);
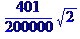
Как видно из примера 2, использование команды без параметров не упростило выражения ln(exp(x))+x·ln(exp(x)), тогда как второй оператор с предположением о действительной области изменения переменной х упростил заданное выражение. Maple по умолчанию работает с комплексными числами (т.е. при упрощении предполагается, что переменные изменяются в области комплексных чисел). При таком предположении упростить выражение с действительно невозможно.
Пример 3. Упрощение с предположением.
> f:=(sqrt(x^2));
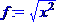
> simplify(f);
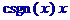
> simplify(f,assume=real);

> simplify(f,assume=positive);
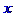
Команда simplify() позволяет задать правила упрощения в виде равенств. Эти правила задаются вторым параметром, который должен иметь следующий вид:
{равенствоl, равенство2,...}
Использование собственных правил для упрощения тригонометрических выражений позволяет получить именно тот его вид, который необходим для дальнейшей работы, так как третьим параметром можно определить, в какой последовательности должны отображаться неизвестные в упрощенном выражении. Этот параметр задается в двух формах: в виде множества и в виде списка. (Множество – последовательность выражений через запятую, заключенная в фигурные скобки, а список - это тоже объект Maple, который для данного частного случая можно охарактеризовать как последовательность выражений через запятую, заключенную в квадратные скобки.) Так вот, если параметр задан в виде множества, то алгоритм упрощения сортирует в выражении неизвестные по убыванию их степени в слагаемых выражения, учитывая степени всех неизвестных, а потом начинает упрощения в соответствии с заданными правилами. В случае со списком – сначала выражение сортируется по степеням первой неизвестной в списке, затем упрощается в соответствии с заданными правилами, затем полученное выражение сортируется по степеням второй неизвестной списка и упрощается и т. д.
Пример 4. Упрощение в соответствии с правилами пользователя.
> equ:={sin(x)^2+cos(x)^2=1};e:=sin(x)^3-11*sin(x)^2*cos(x)+3*cos(x)^3-sin(x)*cos(x)+2;
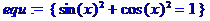
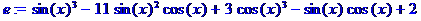
> simplify(e,equ,[sin(x),cos(x)]);

> simplify(e,equ,[cos(x),sin(x)]);

Пример 5. Представление произведений в виде суммы.
> expand((x+3)*(x+4)^2);
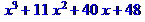
> expand((x+3)^3/(x+4)^2);
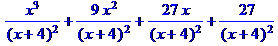
> expand(cos(x-y));
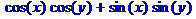
> expand((x+3)*(x+4)^2,x+3);
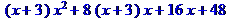
Пример 6. Разложение полинома над разными полями.
> factor(x^3+2); #над полем целых чисел (целые коэффициенты)
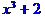
> factor(x^3+2.0); #над полем вещественных чисел
(вещественный коэффициент)
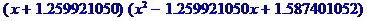
> factor(x^3+2,real); #над полем вещественных чисел
(параметр real)
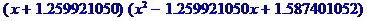
> factor(x^3+2,complex); #над полем комплексных чисел
(параметр complex)
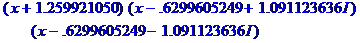
> factor(x^3+2,2^(1/3)); #над полем целых и радикала 2^(1/3)
(параметр определяет поле с радикалом)
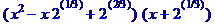
Если применить команду factor () к алгебраической рациональной дроби (отношение двух полиномов), то сначала будет осуществлено приведение дроби к нормальной форме (сокращение общих множителей числителя и знаменателя), а после этого и числитель, и знаменатель раскладываются на множители (с учетом поля коэффициентов):
> d:=(x^11-y^11)/(x^6-y^6);
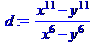
> factor(d);
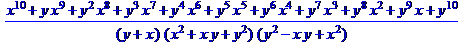
Пример 7.Сокращение алгебраических дробей.
> f:=1/x+1/(x+1)^2+1/(x+1);
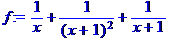
> normal(f);
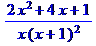
Если параметр f задан в виде списка, множества, последовательности, ряда, уравнения, отношения или функции, то команда normal () последовательно применяется к компонентам f. Например, для уравнения это означает, что процедура сокращения применяется и к правой, и к левой части уравнения. В случае ряда, это означает, что упрощаются коэффициенты ряда, а в случае выражения с несколькими функциями, аргументы которых представлены алгебраическими дробями, процедура сокращения применяется к аргументу каждой функции:
> s:=sin(x/(x+1)-x)^2+cos(-x/(x+1)+x);
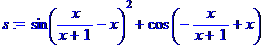
> normal(s);
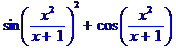
> normal(1/x+y=x/y+(3*y)/x);
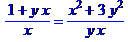
Пример 8. Приведение коэффициентов в выражении.
>k:=x^3*sin(x)^2+x^3*cos(x)+x^3*exp(x)+x*cos(x)+2*x*exp(x)+7*x*sin(x)+4*x^3;
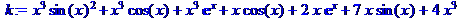
> collect(k,x);
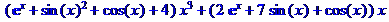
> collect(k,x^3);
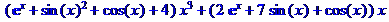
> collect(k,exp(x));
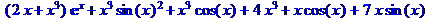
> collect(k,sin(x));
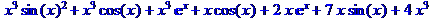
> collect(k,cos(x));

В примере 8 для одного и того же выражения осуществляется приведение коэффициентов относительно разных его неизвестныхкомпонентов.
Параметр form применяется для полиномов от нескольких переменных и определяет алгоритм приведения подобных членов. Заметим, что неизвестные, при степенях которых приводятся подобные члены, должны быть заданы в виде списка или множества. Параметр form два значения: recursive и distributed. В первом случае приводятся подобные члены при степенях первой неизвестной в списке, затем в полученных коэффициентах приводятся подобные члены относительно степеней второй неизвестной в списке и т. д. Если при этом значении параметра form неизвестные полинома, относительно которых приводятся подобные члены, заданы в виде множества, то порядок приведения определяется системой Maple и может меняться от сеанса к сеансу. Значение distributed указывает на приведение коэффициентов при членах, содержащих всевозможные произведения степеней неизвестных в списке или множестве, причем суммарная степень всех переменных возрастает от наименьшей к наибольшей.
Пример 9. Алгоритмы приведения для полиномов нескольких переменных.
> p:=x*y-a^2*x*y+y*x^2-a*y*x^2+x+a*x; #полином двух переменных

> collect(p,[x,y],recursive);

> collect(p,[y,x],recursive);

> collect(p,{x,y},recursive);

> collect(p,{x,y},distributed);

> collect(p,[x,y],distributed);

Параметр func определяет имя команды, применяемой к полученным в результате коэффициентам при соответствующих степенях неизвестных. Обычно используют команды simplify () и factor ().
Пример 10. Задание функции, применяемой к полученным коэффициентам.
> d:=a^4*y-y+a^4+a^2;

> collect(d,y);

> collect(d,y,factor); # разложение на множители коэффициентов при y

Пример 11. Рационализация дробных выражений.
> a:=7*(3^(1/3)+4^(1/5))/(3-2^(1/3));

> rationalize(a);
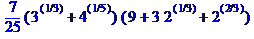
> b:=y/(y+sqrt(2-sqrt(5)));
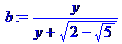
> rationalize(b);
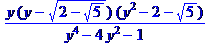
> c:=1/(3-root(cos(1/(2+sqrt(mu))),5));
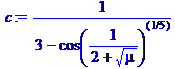
> rationalize(c);
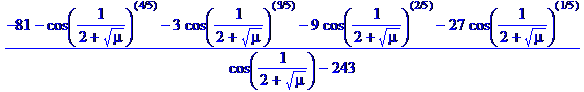
Задачи для самостоятельного решения.
1. Исключить иррациональность в дроби:
1.1. 
1.2. 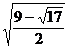
1.3. 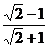
1.4. 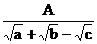
1.5 
1.6 
2. Разложить многочлен на множители:
2.1. 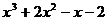
2.2. 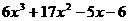
2.3. 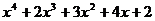
2.4. 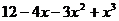
2.5. 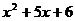
2.6. 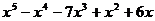
2.7. 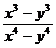
3. Раскрыть скобки в выражении:
3.1. 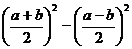
3.2. 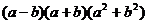
3.3. 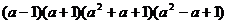
3.4. 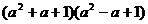
3.5. 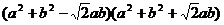
3.6. 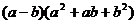
3.7. 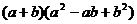
3.8. 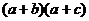
4. Привести к одному члену:
4.1. 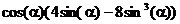
4.2. 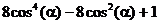
4.3. 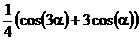
4.4. 
4.5. 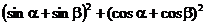
4.6. 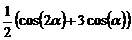
5. С помощью команд преобразования выражений получить равенство:
5.1. 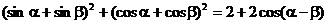
5.2. 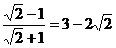
5.3. 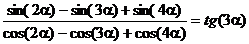
5.4. 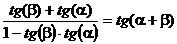
5.5. 
5.6. 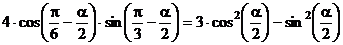
5.7. 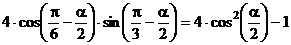
5.8. 
5.9. 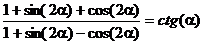
5.10. 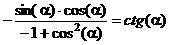
5.11. 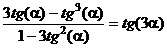
5.12. 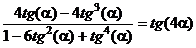
5.13. 
5.14. 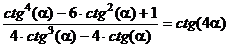
Контрольные вопросы.
1. Команда simplify (), ее предназначение и синтаксис.
2. Команда expand (), ее предназначение и синтаксис.
3. Команда factor (), ее предназначение и синтаксис.
4. Команда normal (), ее предназначение и синтаксис.
5. Команда combine (), ее предназначение и синтаксис.
6. Команда collect (), ее предназначение и синтаксис.
7. Команда rationalize (), ее предназначение и синтаксис.
Задание № 2.
ИСПОЛЬЗОВАНИЕ КОМАНД ПРЕОБРАЗОВАНИЯ ВЫРАЖЕНИЙ MAPLE ДЛЯ МАТЕМАТИЧЕСКИХ ВЫЧИСЛЕНИЙ.
Цели работы:
· знать команды, наиболее часто используемые при выполнении
аналитических вычислений;
· уметь применять указанные команды для решения математических
задач.
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.
1. Команды преобразования выражений.
Процесс работы в Maple состоит в том, что пользователь создает переменные, присваивает им символьные выражения и производит над ними некоторые действия в соответствии с алгоритмом решения поставленной задачи, использую стандартные функции или написанные собственные процедуры.
Синтаксис вызова стандартной команды следующий:
команда (пар_1, пар_2,..., пар_n);
Здесь команда - это имя вызываемой функции, а пар_1, пар_2,... означают необходимые для выполнения команды параметры, которые могут быть переменными или даже выражениями, причем их тип должен соответствовать типу параметров используемой функции. Отметим, если команда завершается точкой с запятой, то результаты ее выполнения отображаются в области вывода, если команда завершается двоеточием, то она выполняется, но никакого вывода результатов не происходит.
Система обозначений функций в Maple интуитивно проста. Обычно имя функции соответствует действию, которое она выполняет (следует учесть, что все имена заданы на английском языке). Например, ясно, что функция с именем simplify () осуществляет некоторые упрощения над выражением, заданным в качестве ее параметра.
Для некоторых команд существуют активная и пассивная формы. Активная форма команды (в случае ее вызова) немедленно выполняется, а ее имя начинается со строчной буквы. Пассивная форма команды не выполняется немедленно, а просто в области вывода отображается математическая запись того, что она может сделать. Ее имя начинается с прописной буквы. В дальнейшем, если в операторе присваивания для некоторой переменной в правой части задана пассивная форма команды, то командой value () ее можно вычислить. Основное предназначение пассивных форм команд - это использование их как средства документирования производимых действий в обычной математической нотации. Примерами команд с двумя формами являются команда дифференцирования (diff и Diff), интегрирования (int и Int) и др.
Пример 1. Пассивная и активная формы команд.
> k:=Int(cos(x)^3,x);
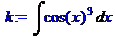
> k=int(cos(x)^3,x);

> value(k);
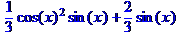
Если команды и функции являются частью ядра системы Maple, то они всегда доступны пользователю. А для вызова других команд и функций необходимо подключить библиотеку или пакет, в которых они расположены. Для этого служат команды readlib () и with (). Первая подключает библиотеку, вторая - пакет. Параметром этих команд является имя библиотеки или пакета, функции которых пользователь желает использовать.
Команды и функции Maple, наиболее часто используемые при аналитических преобразованиях, располагаются в его системном ядре – части программного обеспечения системы аналитических вычислений, постоянно находящейся в памяти компьютера. К ним относятся команды, выполняющие разнообразные преобразования выражений, получающие решение уравнений и систем уравнений, дифференцирующие функции и т. д. В данной работе вводятся команды, наиболее часто используемые при выполнении аналитических вычислений.
Упрощение выражения: simplify ().
Команда simplify () предназначена для упрощения разнообразных выражений, составленных из чисел, переменных и элементарных функций. Заметим, что Maple может его упростить, а может и не упростить, так как он использует свои внутренние алгоритмы упрощения, результат выполнения которых может не совсем соответствовать взглядам пользователя на то, как он хотел бы упростить выражение и в каком виде его получить.
Эта команда имеет несколько форм вызова. Ее самый простой синтаксис имеет следующий вид:
simplify (выражение);
В скобках указывается выражение, подлежащее упрощению. Команда simplify () ищет в выражении вызовы функций, квадратные корни, радикалы и степени и инициализирует подходящие процедуры упрощения. Реально команда simplify () реализована в виде набора процедур упрощения, хранящихся в основной библиотеке Maple. Перечислим некоторые из них, остальные можно найти в справке по этой команде (например, установив курсор в рабочем листе на ее имя и нажав клавишу <F1>): `simplify/exp` - для упрощения выражений с экспоненциальными функциями, `simрlifу/ln` - для упрощения выражений с логарифмами, `simplifу/sqrt` - для упрощения выражений, содержащих квадратные корни, `simplifу/trig` - для упрощения выражении с тригонометрическими функциями, `simplifу/radical` - для упрощения выражений с радикалами (дробные степени), `simplifу/power` - для упрощения выражений со степенями, экспонентами и логарифмами и т.д. По умолчанию Maple пытается использовать максимальный набор функций упрощения, подходящий к конкретному выражению.
В команде можно задать конкретные процедуры упрощения, и тогда только они будут использоваться для упрощения заданного выражения, а не весь возможный, установленный по умолчанию набор. Это обеспечивается следующим синтаксисом команды:
simрlifу(выражение, nl, n2,...);
Здесь nl, n2 и т. д. являются именами процедур упрощения: Ei, GAMМА, RootOf, @, hypergeom, ln, polar, power, radical, sqrt, trig. Полную информацию о формулах упрощения при использовании перечисленных значений параметров можно получить с помощью команды?simplify [имя], где [имя] - одно из значений параметров функции упрощения.
Упрощения выражений можно проводить с различными видами чисел, например, положительными или принадлежащими некоторому отрезку действительных чисел. Это достигается с помощью параметра assume=свойство. Форма вызова команды при этом имеет вид:
simplify (выражение, аssumе=свойство);
где параметр свойство может принимать одно из следующих значений:
complex - комплексная область, real - действительная область, positive - положительные действительные числа, integer - целые числа, RealRange(a,b) - интервал (а,b) действительных чисел.
Примеры использования команды упрощения выражений simplify() представлены ниже:
Пример 2. Упрощение выражений.
> c:=ln(exp(x))+x*ln(exp(x));
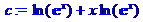
> simplify(c);
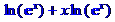
> simplify(c,assume=real);
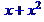
> d:=1/sqrt(8)*(((1+sqrt(8))/10)^5+((1-sqrt(8))/10)^5);

> simplify(d);
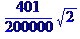
Как видно из примера 2, использование команды без параметров не упростило выражения ln(exp(x))+x·ln(exp(x)), тогда как второй оператор с предположением о действительной области изменения переменной х упростил заданное выражение. Maple по умолчанию работает с комплексными числами (т.е. при упрощении предполагается, что переменные изменяются в области комплексных чисел). При таком предположении упростить выражение с действительно невозможно.
Пример 3. Упрощение с предположением.
> f:=(sqrt(x^2));
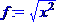
> simplify(f);
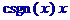
> simplify(f,assume=real);

> simplify(f,assume=positive);
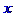
Команда simplify() позволяет задать правила упрощения в виде равенств. Эти правила задаются вторым параметром, который должен иметь следующий вид:
{равенствоl, равенство2,...}
Использование собственных правил для упрощения тригонометрических выражений позволяет получить именно тот его вид, который необходим для дальнейшей работы, так как третьим параметром можно определить, в какой последовательности должны отображаться неизвестные в упрощенном выражении. Этот параметр задается в двух формах: в виде множества и в виде списка. (Множество – последовательность выражений через запятую, заключенная в фигурные скобки, а список - это тоже объект Maple, который для данного частного случая можно охарактеризовать как последовательность выражений через запятую, заключенную в квадратные скобки.) Так вот, если параметр задан в виде множества, то алгоритм упрощения сортирует в выражении неизвестные по убыванию их степени в слагаемых выражения, учитывая степени всех неизвестных, а потом начинает упрощения в соответствии с заданными правилами. В случае со списком – сначала выражение сортируется по степеням первой неизвестной в списке, затем упрощается в соответствии с заданными правилами, затем полученное выражение сортируется по степеням второй неизвестной списка и упрощается и т. д.
Пример 4. Упрощение в соответствии с правилами пользователя.
> equ:={sin(x)^2+cos(x)^2=1};e:=sin(x)^3-11*sin(x)^2*cos(x)+3*cos(x)^3-sin(x)*cos(x)+2;
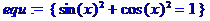
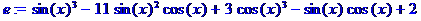
> simplify(e,equ,[sin(x),cos(x)]);

> simplify(e,equ,[cos(x),sin(x)]);