Так как уравнение напряженного состояния, так же как и уравнения неразрывности и движения, записываются для жидкостей и газов одинаково, то под словом «жидкости» будем одновременно подразумевать и газы.
Силы трения связаны со скоростями деформации. Поэтому начать следует с разделения суммарной скорости жидкой частицы 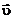 на составляющие:
на составляющие: 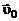 – скорость поступательного движения вместе с выбранным центром – точкой О,
– скорость поступательного движения вместе с выбранным центром – точкой О, 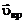 – скорость вращательного движения относительно этого центра и
– скорость вращательного движения относительно этого центра и 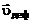 – скорость деформационного движения, т.е.
– скорость деформационного движения, т.е.
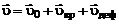 . (2.3.1)
. (2.3.1)
Угловую скорость вращательного движения, зная поле скоростей, найдем через так называемый вихревой вектор  .
.
Вихревым вектором поля скоростей 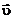 называется вектор, проекция которого на каждое направление равна пределу отношения циркуляции векторного поля по контуру
называется вектор, проекция которого на каждое направление равна пределу отношения циркуляции векторного поля по контуру 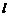 плоской площадки
плоской площадки 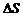 , перпендикулярной этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю:
, перпендикулярной этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю:
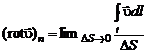 . (2.3.2)
. (2.3.2)
Нормаль 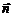 к площадке направляется так, чтобы при вычислении циркуляции обход по контуру
к площадке направляется так, чтобы при вычислении циркуляции обход по контуру 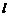 казался совершающимся против часовой стрелки.
казался совершающимся против часовой стрелки.
Покажем, что вектор  и вектор угловой скорости вращения жидкой частицы
и вектор угловой скорости вращения жидкой частицы 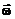 связаны простым соотношением
связаны простым соотношением
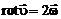 . (2.3.3)
. (2.3.3)
Для доказательства в качестве контура интегрирования возьмем окружность радиуса r с центром, совмещенным с центром вращения, а нормаль 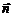 к элементарной площадке
к элементарной площадке 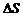 будем последовательно совмещать с координатными осями. Так как скорость
будем последовательно совмещать с координатными осями. Так как скорость 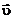 при вращении жидкой частицы как твердого тела равна:
при вращении жидкой частицы как твердого тела равна:
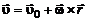 , (2.3.4)
, (2.3.4)
где через 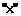 обозначено векторное произведение, то
обозначено векторное произведение, то
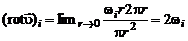 , (2.3.5)
, (2.3.5)
что доказывает равенство (2.3.3), из которого следует, что скорость вращательного движения
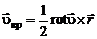 . (2.3.6)
. (2.3.6)
Запишем выражение для проекций вектора  на оси декартовой системы координат.
на оси декартовой системы координат.
Используем для сокращения записи следующий прием. Пусть задан набор из 27 чисел 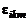 (каждый из индексов меняется от 1 до 3). Зададим эти числа следующим образом:
(каждый из индексов меняется от 1 до 3). Зададим эти числа следующим образом:
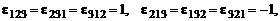 (2.3.7)
(2.3.7)
а все остальные значения 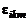 приравняем нулю.
приравняем нулю.
Тогда с учетом принципа суммирования по повторяющемуся индексу проекции вихревого вектора  на оси равны:
на оси равны:
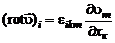 . (2.3.8)
. (2.3.8)
Из соотношения (2.3.8) следует, что
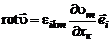 . (2.3.9)
. (2.3.9)
Подставляя в уравнение (2.3.1) выражение (2.3.6), получим формулу для вычисления скорости деформационного движения в виде
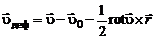 . (2.3.10)
. (2.3.10)
Используя оператор 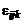 для записи векторного произведения в проекциях на оси координат:
для записи векторного произведения в проекциях на оси координат:
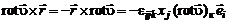 (2.3.11)
(2.3.11)
и разлагая скорость 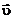 по координатным осям в ряд Тейлора относительно центра вращения, ограничиваясь в разложении первыми производными
по координатным осям в ряд Тейлора относительно центра вращения, ограничиваясь в разложении первыми производными
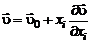 , (2.3.12)
, (2.3.12)
получим
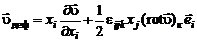 , (2.3.13)
, (2.3.13)
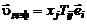 , (2.3.14)
, (2.3.14)
где
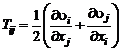 . (2.3.15)
. (2.3.15)
Из полученных значений  можно составить таблицу из девяти величин, называемую тензором скоростей деформации.
можно составить таблицу из девяти величин, называемую тензором скоростей деформации.
Напомним некоторые понятия тензорного исчисления.
Рассмотрим две декартовы системы координат: 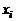 и
и 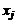 . Их взаимное расположение характеризуется таблицей направляющих косинусов
. Их взаимное расположение характеризуется таблицей направляющих косинусов
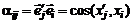 , (2.3.16)
, (2.3.16)
где 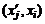 – угол между ортами осей. Так как скалярное произведение не зависит от порядка сомножителей, то очевидно, что
– угол между ортами осей. Так как скалярное произведение не зависит от порядка сомножителей, то очевидно, что 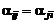 .
.
Если в каждой декартовой системе координат задана таблица величин с N индексами 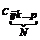 , где каждый индекс принимает значения от 1 до 3, и если элементы этой таблицы при переходе от одной системы координат к другой преобразуются по формулам
, где каждый индекс принимает значения от 1 до 3, и если элементы этой таблицы при переходе от одной системы координат к другой преобразуются по формулам
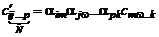 , (2.3.17)
, (2.3.17)
то говорят, что совокупность величин 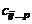 образует аффинный ортогональный тензор ранга N.
образует аффинный ортогональный тензор ранга N.
Вывод уравнений напряженного состояния для пространственного движения жидкости опирается на два постулата.
Первый постулат: элементы тензора напряжений сил трения 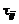 линейно зависят от элементов тензора скоростей деформа-
линейно зависят от элементов тензора скоростей деформа-
ции  :
:
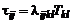 , (2.3.18)
, (2.3.18)
где 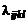 – тензор четвертого ранга, описывающий свойства среды.
– тензор четвертого ранга, описывающий свойства среды.
Второй постулат: среда изотропна. Это означает, что элементы тензора 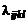 должны сохранять свои значения при любом повороте координатной системы.
должны сохранять свои значения при любом повороте координатной системы.
Изотропный тензор четвертого ранга является линейной комбинацией всех возможных произведений изотропных тензоров второго ранга:
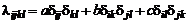 , (2.3.19)
, (2.3.19)
где 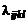 – изотропный тензор четвертого ранга; a, b, c – постоянные;
– изотропный тензор четвертого ранга; a, b, c – постоянные; 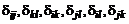 – единичные тензоры второго ранга.
– единичные тензоры второго ранга.
Элементы единичного тензора второго ранга равны:
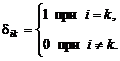 (2.3.20)
(2.3.20)
Тензор 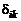 , называемый также символом Кронекера, обладает свойством изотропности.
, называемый также символом Кронекера, обладает свойством изотропности.
Подставляя выражение для 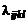 (2.3.19) в формулу (2.3.18), с учетом (2.3.20) получим
(2.3.19) в формулу (2.3.18), с учетом (2.3.20) получим
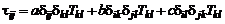 ,
,
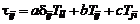 . (2.3.21)
. (2.3.21)
Так как тензор скоростей деформации является симметричным тензором 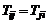 (см. формулу (2.3.15)), то, обозначая
(см. формулу (2.3.15)), то, обозначая 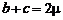 и
и 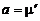 , получим обобщенный закон Ньютона:
, получим обобщенный закон Ньютона:
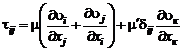 , (2.3.22)
, (2.3.22)
где 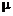 – коэффициент динамической вязкости.
– коэффициент динамической вязкости.
Если в движущемся газе в каждой точке успевает установиться термодинамическое равновесие, то справедливо еще одно утверждение:
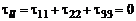 . (2.3.23)
. (2.3.23)
Условие (2.3.23) позволяет из соотношения (2.3.22) получить значение 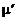 :
:
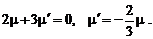 (2.3.24)
(2.3.24)
Таким образом, при заданном поле скоростей тензор вязких напряжений (2.3.22), (2.3.24) будет содержать лишь одну неизвестную – коэффициент динамической вязкости 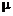 , который либо определяется из опыта, либо рассчитывается на основе молекулярно-кинетической теории газа.
, который либо определяется из опыта, либо рассчитывается на основе молекулярно-кинетической теории газа.
Заметим, что обобщенный закон Ньютона в виде соотношений (2.3.22), (2.3.24) справедлив как для однокомпонентного газа, так и для смеси. Различие будет лишь в значениях 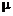 .
.
Уравнение энергии
Введем ряд новых понятий, которые нам потребуются в процессе вывода уравнения энергии:
· E – полная энергия единицы массы газа:
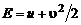 , (2.4.1)
, (2.4.1)
где u – внутренняя энергия единицы массы газа;  – кинетическая энергия единицы массы газа;
– кинетическая энергия единицы массы газа;
· H – полное теплосодержание (энтальпия) единицы массы газа:
 , (2.4.2)
, (2.4.2)
где 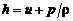 – теплосодержание (энтальпия) единицы массы газа;
– теплосодержание (энтальпия) единицы массы газа;
· 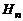 – обобщенное полное теплосодержание (энтальпия) с учетом стандартной теплоты образования и теплоты фазовых и полиморфных превращений:
– обобщенное полное теплосодержание (энтальпия) с учетом стандартной теплоты образования и теплоты фазовых и полиморфных превращений:
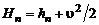 , (2.4.3)
, (2.4.3)
где 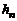 – обобщенное теплосодержание (энтальпия) с учетом стандартной теплоты образования и теплоты фазовых и полиморфных превращений. Значение
– обобщенное теплосодержание (энтальпия) с учетом стандартной теплоты образования и теплоты фазовых и полиморфных превращений. Значение 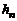 для смеси газов определяется по соотношениям (1.2.40) – (1.2.43).
для смеси газов определяется по соотношениям (1.2.40) – (1.2.43).
Сформулируем закон изменения полной энергии: изменение полной энергии некоторой массы газа, состоящей из одних и тех же жидких частиц, в единицу времени равно мощности всех внешних сил, действующих на выделенную массу газа, плюс количество тепла, которое получает данная масса газа от окружающей среды в единицу времени.
Изменение полной энергии в единицу времени (производная от полной энергии по времени) равно:
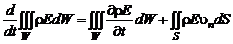 . (2.4.4)
. (2.4.4)
Силы, рассмотренные в подразд. 2.2, производят над выделенной массой газа в единицу времени следующую работу:
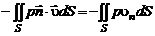 – мощность сил давления;
– мощность сил давления;
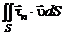 – мощность сил трения;
– мощность сил трения;
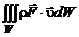 – мощность массовых сил,
– мощность массовых сил,
где точкой обозначено скалярное произведение, т.е., например, 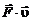 – скалярное произведение векторов
– скалярное произведение векторов 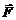 и
и 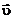 .
.
Тепло, поступающее от окружающей среды, складывается из тепла, поступающего через граничную поверхность 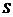 , и тепла, излучаемого или поглощаемого выделенной массой газа.
, и тепла, излучаемого или поглощаемого выделенной массой газа.
Обозначим через  вектор потока тепла, проходящего через единичную площадку в единицу времени. Тогда через граничную поверхность
вектор потока тепла, проходящего через единичную площадку в единицу времени. Тогда через граничную поверхность 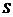 внутрь объема попадет количество тепла, равное:
внутрь объема попадет количество тепла, равное:
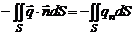 ,
,
где знак «-» показывает, что тепло поступает внутрь объема W,т.е. в сторону, обратную направлению внешней нормали 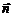 .
.
Обозначим через 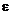 количество тепла, поступающего от окружающей среды к единице массы газа в единицу времени. В величину
количество тепла, поступающего от окружающей среды к единице массы газа в единицу времени. В величину 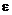 , в частности, может быть включена химическая энергия, выделяющаяся при прохождении химических реакций между компонентами смеси. Однако если вместо теплосодержания h использовать обобщенное теплосодержание
, в частности, может быть включена химическая энергия, выделяющаяся при прохождении химических реакций между компонентами смеси. Однако если вместо теплосодержания h использовать обобщенное теплосодержание 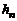 , то
, то 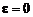 , так как значение
, так как значение 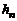 не меняется при протекании химических реакций. Суммарное объемное поступление тепла от окружающей среды в единицу времени равно:
не меняется при протекании химических реакций. Суммарное объемное поступление тепла от окружающей среды в единицу времени равно:
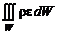 .
.
В соответствии с законом изменения энергии
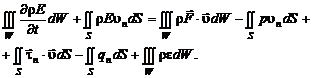 (2.4.5)
(2.4.5)
Уравнение (2.4.5) представляет собой закон изменения энергии в интегральной форме.
В ряде случаев удобнее вместо полной энергии Е использовать полное теплосодержание H. Выполним следующие преобразования. Учтем, что в соответствии с формулами (2.4.1) и (2.4.2)
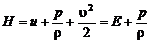 . (2.4.6)
. (2.4.6)
Тогда
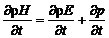 , (2.4.7)
, (2.4.7)
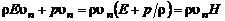 . (2.4.8)
. (2.4.8)
Подставляя (2.4.7) и (2.4.8) в формулу (2.4.5), получим уравнение энергии в интегральной форме:
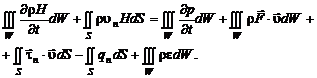 (2.4.9)
(2.4.9)
Если массовое выделение тепла 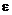 происходит только из-за химических реакций, то, вводя вместо полного теплосодержания H обобщенное полное теплосодержание
происходит только из-за химических реакций, то, вводя вместо полного теплосодержания H обобщенное полное теплосодержание 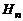 , получим уравнение энергии для смеси:
, получим уравнение энергии для смеси:
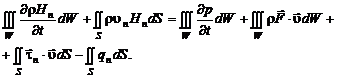 (2.4.10)
(2.4.10)
В виде (2.4.10) уравнение энергии справедливо для течений газа как при наличии, так и при отсутствии химических реакций.
Получим интегральную форму записи уравнения энергии для турбулентной струи, истекающей в затопленное пространство или спутный поток.
Примем следующие допущения:
· массовые силы пренебрежимо малы;
· движение установившееся;
· параметры в окружающей среде постоянны;
· в струе выполняются условия для пограничного слоя: силы трения велики лишь на площадках с внешней нормалью, перпендикулярной оси; тепловые потоки существенны только в поперечном направлении.
Как и при выводе уравнения движения, выделим объем W, заключенный между сечением, проходящем через срез сопла, и любым другим сечением вниз по потоку. Тогда из формулы (2.4.10) следует интегральное соотношение: суммарный поток избыточного обобщенного теплосодержания сохраняется по длине струи:
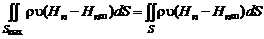 , (2.4.11)
, (2.4.11)
где 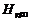 – обобщенное теплосодержание единицы массы газа окружающей среды.
– обобщенное теплосодержание единицы массы газа окружающей среды.
Интегральное соотношение (2.4.11) справедливо для самых различных типов турбулентных струй: изотермических, неизотермических и струй с диффузионным факелом горения.
Перейдем к выводу уравнения энергии в дифференциальной форме в декартовой системе координат. Для этого разделим равенство (2.4.9) на элементарный объем с гранями, параллельными координатным плоскостям, и перейдем к пределу, стягивая объем в точку. В результате получим
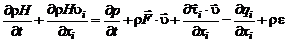 . (2.4.12)
. (2.4.12)
Преобразуем левую часть уравнения (2.4.12):
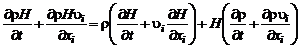 .
.
Так как в силу уравнения неразрывности
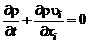 , (2.4.13)
, (2.4.13)
а полная производная
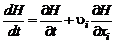 , (2.4.14)
, (2.4.14)
то уравнение (2.4.12) приводится к виду
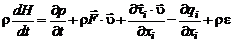 . (2.4.15)
. (2.4.15)
При расчете течений с физико-химическими превращениями в уравнении (2.4.15) следует полное теплосодержание H заменить на обобщенное полное теплосодержание 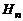 , исключив в правой части слагаемое
, исключив в правой части слагаемое  .
.
Тепловой поток  для однокомпонентной смеси определяется законом теплопроводности Фурье:
для однокомпонентной смеси определяется законом теплопроводности Фурье:
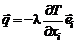 , (2.4.16)
, (2.4.16)
где  – коэффициент теплопроводности.
– коэффициент теплопроводности.
Если газ представляет собой смесь, то появляется дополнительный перенос тепла, вызванный молекулярной диффузией. Введем среднемассовую скорость j -го компонента 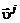 , определив ее как математическое ожидание скорости молекул j -го сорта. Тогда среднемассовая скорость жидкой частицы будет равна (см. формулу (2.1.3)):
, определив ее как математическое ожидание скорости молекул j -го сорта. Тогда среднемассовая скорость жидкой частицы будет равна (см. формулу (2.1.3)):
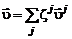 ;
;  , (2.4.17)
, (2.4.17)
где индексом j вверху обозначен номер компоненты (не путать с возведением в степень!).
Диффузионный поток j -го компонента
 (2.4.18)
(2.4.18)
связан с тем, что средняя скорость j -й компоненты отличается от средней скорости смеси в целом. Переносимое тепло вследствие молекулярной диффузии определяется суммой произведений  – при смешении без химических реакций между компонентами либо в более общем виде
– при смешении без химических реакций между компонентами либо в более общем виде 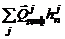 – если смешение может сопровождаться химическими реакциями.
– если смешение может сопровождаться химическими реакциями.
С учетом молекулярной диффузии уравнение энергии для смеси запишем в виде
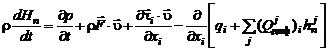 . (2.4.19)
. (2.4.19)
Преобразуем уравнение энергии (2.4.15) к форме, используемой при формулировке первого закона термодинамики.
Раскроем производную
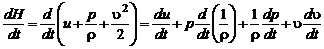 . (2.4.20)
. (2.4.20)
Покажем, что
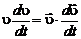 . (2.4.21)
. (2.4.21)
Так как левые части выражений
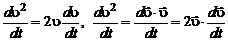 (2.4.22)
(2.4.22)
равны, то равны соответственно и правые части, что доказывает тождество (2.4.21).
Далее умножим уравнение движения (2.2.18) скалярно на скорость 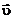 :
:
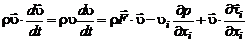 (2.4.23)
(2.4.23)
и подставим значения 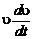 в (2.4.20). Получим
в (2.4.20). Получим
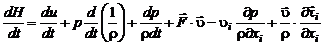 . (2.4.24)
. (2.4.24)
Заменив производную 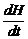 в левой части (2.4.15) ее выражением с помощью равенства (2.4.24), получим
в левой части (2.4.15) ее выражением с помощью равенства (2.4.24), получим
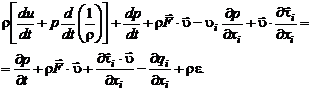 (2.4.25)
(2.4.25)
Подставляя в (2.4.25) значение полной производной
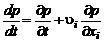 (2.4.26)
(2.4.26)
и раскрывая производную от произведения 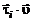
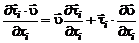 , (2.4.27)
, (2.4.27)
после приведения подобных членов получим уравнение энергии в форме первого начала термодинамики:
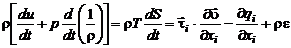 . (2.4.28)
. (2.4.28)
Входящая в правую часть уравнения энергии (2.4.28) диссипативная функция 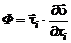 всегда положительна или равна нулю. Это позволяет судить о направлении процесса и сформулировать второе начало термодинамики: в теплоизолированной системе энтропия S либо возрастает, либо остается постоянной
всегда положительна или равна нулю. Это позволяет судить о направлении процесса и сформулировать второе начало термодинамики: в теплоизолированной системе энтропия S либо возрастает, либо остается постоянной 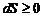 .
.
Уравнение диффузии
Применим закон сохранения массы (см. раздел 2.1) к отдельно взятому j -му компоненту смеси. Учтем, что в химически активной смеси могут проходить реакции, приводящие к образованию или исчезновению j -го компонента.
Введем обозначения:
· 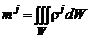 – масса j -го компонента, заключенного в момент времени t внутри произвольно выбранного объема W;
– масса j -го компонента, заключенного в момент времени t внутри произвольно выбранного объема W;
·  – масса j -го компонента, который образуется в единицу времени в единице объема вследствие химических реакций;
– масса j -го компонента, который образуется в единицу времени в единице объема вследствие химических реакций;
· 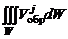 – масса j -го компоненты, который образуется в единицу времени внутри произвольно выбранного объема вследствие химических реакций.
– масса j -го компоненты, который образуется в единицу времени внутри произвольно выбранного объема вследствие химических реакций.
Изменение массы j-го компонента смеси в единицу времени равно скорости образования j-го компонента в выделенной массе газа вследствие химических реакций:
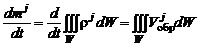 . (2.5.1)
. (2.5.1)
Раскрывая производную по времени, получим
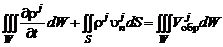 . (2.5.2)
. (2.5.2)
Скорость j -го компонента смеси может отличаться от скорости смеси в целом (см. формулу (2.1.3)). В результате возникает диффузия j -го компонента через граничную поверхность S. Скорость диффузии равна:
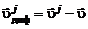 . (2.5.3)
. (2.5.3)
Подставляя соотношение (2.5.3) для скорости диффузии j -го компонента в (2.5.2), получим
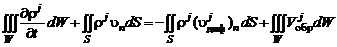 . (2.5.4)
. (2.5.4)
Если ввести вектор потока диффузии j -го компонента 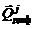 (см. (2.4.18)), то получим уравнение диффузии в интегральной форме:
(см. (2.4.18)), то получим уравнение диффузии в интегральной форме:
 . (2.5.5)
. (2.5.5)
При решении практических задач, связанных с движением смеси газов, удобнее пользоваться не размерными плотностями компонентов смеси 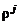 , а безразмерными массовыми концентрациями
, а безразмерными массовыми концентрациями 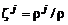 . Заменяя в (2.5.5) значение
. Заменяя в (2.5.5) значение 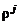 выражением
выражением 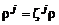 , приведем уравнение диффузии к виду
, приведем уравнение диффузии к виду
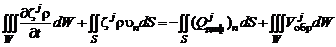 . (2.5.6)
. (2.5.6)
В тех случаях, когда смешение сопровождается равновесными химическими реакциями, следует уравнение диффузии записывать для концентраций химических элементов, поскольку, в отличие от веществ, концентрация элементов не меняется. Следовательно, скорость образования химических элементов равна нулю, и закон сохранения массы i -го элемента можно представить формулой
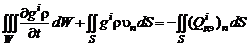 , (2.5.7)
, (2.5.7)
где 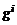 – массовая доля i -го элемента в смеси,
– массовая доля i -го элемента в смеси, 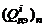 – проекция на внешнюю нормаль вектора потока диффузии i -го химического элемента:
– проекция на внешнюю нормаль вектора потока диффузии i -го химического элемента:
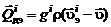 , (2.5.8)
, (2.5.8)
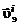 – математическое ожидание скорости i -го элемента.
– математическое ожидание скорости i -го элемента.
Применим полученные уравнения диффузии в интегральной форме к турбулентной струе, истекающей в затопленное пространство или спутный поток на установившемся режиме. Помимо допущений, принятых в подразд. 2.2 и 2.4 при выводе интегральных соотношений движения и энергии, будем полагать, что:
· состав однороден на срезах сопл. Это позволяет одним параметром 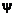 – массовой долей в смеси вещества, истекающего из сопл двигателя, – определить с помощью формул (1.1.12), (1.1.14), (1.1.16) химический состав смеси;
– массовой долей в смеси вещества, истекающего из сопл двигателя, – определить с помощью формул (1.1.12), (1.1.14), (1.1.16) химический состав смеси;
· молекулярной диффузией по сравнению с турбулентной можно пренебречь, т.е. 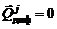 и
и 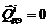 .
.
Тогда из (2.5.6) и (2.5.7) получим интегральное условие сохранения массы вещества, истекающего из двигателей:
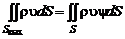 . (2.5.9)
. (2.5.9)
Выведем уравнение диффузии в дифференциальной форме в декартовой системе координат. Выделим параллелепипед с гранями, параллельными координатным плоскостям. Разделим (2.5.6) на объем этого параллелепипеда и перейдем к пределу, устремляя объем к нулю. В результате получим уравнение диффузии в дифференциальной форме:
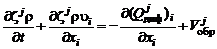 . (2.5.10)
. (2.5.10)
Запишем это уравнение. Преобразуем левую часть (2.5.10):
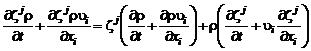 . (2.5.11)
. (2.5.11)
Так как, в силу уравнения неразрывности (см. (2.1.15))
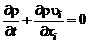 , (2.5.12)
, (2.5.12)
а полная производная
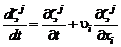 , (2.5.13)
, (2.5.13)
то уравнение (2.5.10) приводится к виду
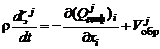 . (2.5.14)
. (2.5.14)
Диффузионный поток j -го компонента можно приближенно представить формулой
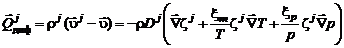 , (2.5.15)
, (2.5.15)
где 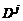 – коэффициент диффузии, определяющий диффузионный поток при наличии только градиента концентрации компонентов смеси
– коэффициент диффузии, определяющий диффузионный поток при наличии только градиента концентрации компонентов смеси 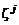 , а
, а 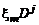 и
и 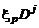 – коэффициенты термодиффузии и бародиффузии, которые определяют соответственно диффузионные потоки, возникающие вследствие градиентов температуры и давления, общих для всех компонентов смеси.
– коэффициенты термодиффузии и бародиффузии, которые определяют соответственно диффузионные потоки, возникающие вследствие градиентов температуры и давления, общих для всех компонентов смеси.
При расчете ламинарных пограничных слоев и ламинарных струй можно в формуле (2.5.15) пренебречь последним членом, поскольку в таких течениях поперечный градиент давления мал и, следовательно, влияние бародиффузии можно не учитывать.
2.6. Методы описания турбулентного движения.
Проблема замыкания системы уравнений Рейнольдса
Задача определения вероятностных характеристик газодинамических параметровпри турбулентном смешении даже для простейших типов течения достаточно сложна. Для того чтобы понять суть возникающих проблем, предельно упростим постановку задачи. Будем считать газ несжимаемым  , массовые силы пренебрежимо малыми, а коэффициент динамической вязкости
, массовые силы пренебрежимо малыми, а коэффициент динамической вязкости 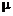 постоянным по всему полю течения. Тогда дифференциальные уравнения движения – уравнения Навье – Стокса – в прямоугольной декартовой системе координат записываются в виде (см. формулы (2.2.18), (2.2.19), (2.3.22)
постоянным по всему полю течения. Тогда дифференциальные уравнения движения – уравнения Навье – Стокса – в прямоугольной декартовой системе координат записываются в виде (см. формулы (2.2.18), (2.2.19), (2.3.22)
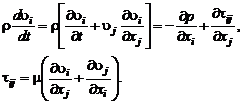 (2.6.1)
(2.6.1)
Система (2.6.1) замыкается с помощью уравнения неразрывности
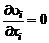 . (2.6.2)
. (2.6.2)
Итак, имеем четыре уравнения (уравнение движения в проекциях на три оси декартовой системы координат (2.6.1) и уравнение неразрывности) для определения четырех неизвестных: трех проекций скорости на оси координат и давления. Решая систему уравнений в частных производных (2.6.1), (2.6.2) при соответствующих начальных и граничных условиях, получим искомые функции 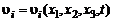 и
и 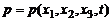 . Казалось бы, имея мощную вычислительную технику, мы без особого труда можем во всех случаях решить уравнения (2.6.1), (2.6.2) численными методами, например методом конечных разностей. Однако в действительности все намного сложнее.
. Казалось бы, имея мощную вычислительную технику, мы без особого труда можем во всех случаях решить уравнения (2.6.1), (2.6.2) численными методами, например методом конечных разностей. Однако в действительности все намного сложнее.
Опыт показывает, что течение, описываемое уравнениями Навье-Стокса, при превышении 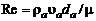 (
(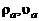 и
и 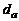 для изобарического участка струи – соответственно плотность, скорость и диаметр струи в начальном сечении) некоторых критических значений становится неустойчивым относительно малых возмущений. В результате потери устойчивости траектории жидких частиц приобретают запутанный, извилистый характер – движение из ламинарного становится турбулентным. Именно с турбулентными течениями мы чаще всего сталкиваемся на практике.
для изобарического участка струи – соответственно плотность, скорость и диаметр струи в начальном сечении) некоторых критических значений становится неустойчивым относительно малых возмущений. В результате потери устойчивости траектории жидких частиц приобретают запутанный, извилистый характер – движение из ламинарного становится турбулентным. Именно с турбулентными течениями мы чаще всего сталкиваемся на практике.
На первый взгляд представляется, что переход течения из ламинарного в турбулентное не очень сильно усложнит решение. В этом случае на начальные и граничные условия следует наложить, сообразуясь с условиями задачи, некоторые случайные колебания и затем статистически обработать полученные случайные величины 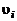 и р. Более подробный анализ показывает, что такой путь может быть реализован только при малых турбулентных числах Рейнольдса. Дело в том, что для адекватного описания течения конечноразностными уравнениями, заменяющими исходные дифференциальные уравнения в частных производных, приходится при турбулентном режиме дробить область течения на очень малые ячейки, размеры которых должны быть порядка самых малых размеров турбулентных вихрей. Сделанные оценки показали, что возможности даже самых мощных вычислительных машин пока недостаточны, чтобы обеспечить при этом требуемые объемы памяти и нужное быстродействие. С развитием вычислительной техники следует ожидать более широкого использования этих методов. Однако обсуждение этого вопроса выходит за рамки данного пособия.
и р. Более подробный анализ показывает, что такой путь может быть реализован только при малых турбулентных числах Рейнольдса. Дело в том, что для адекватного описания течения конечноразностными уравнениями, заменяющими исходные дифференциальные уравнения в частных производных, приходится при турбулентном режиме дробить область течения на очень малые ячейки, размеры которых должны быть порядка самых малых размеров турбулентных вихрей. Сделанные оценки показали, что возможности даже самых мощных вычислительных машин пока недостаточны, чтобы обеспечить при этом требуемые объемы памяти и нужное быстродействие. С развитием вычислительной техники следует ожидать более широкого использования этих методов. Однако обсуждение этого вопроса выходит за рамки данного пособия.
Итак, приходим к выводу, что мы не можем определить статистические характеристики газодинамических параметров в турбулентных течениях и, в частности, в турбулентных струях, решая уравнения для ламинарного течения с последующей статистической обработкой полученных результатов.
В 1881 г. О. Рейнольдс разделил газодинамические параметры на осредненные и пульсационные составляющие и, выполнив операцию осреднения над уравнениями Навье – Стокса, получил уравнения, называемые теперь уравнениями Рейнольдса, в которые характеристики пульсационного движения вошли в явном виде.
Выведем уравнения Рейнольдса. Для этого используем уравнение движения в так называем дивергентном виде (см. формулу (2.2.14)):
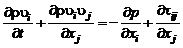 . (2.6.3)
. (2.6.3)
Далее выделим средние значения (математические ожидания) газодинамических параметров и их комбинаций и отклонения от средних – пульсации

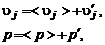 (2.6.4)
(2.6.4)
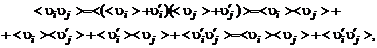 (2.6.5)
(2.6.5)
где знаком  обозначено среднее значение случайной величины, а штрихом вверху – ее пульсационная составляющая. Подставим (2.6.4) в (2.6.1) – (2.6.3). После осреднения преобразованных таким образом уравнений движения и неразрывности получим уравнения Рейнольдса:
обозначено среднее значение случайной величины, а штрихом вверху – ее пульсационная составляющая. Подставим (2.6.4) в (2.6.1) – (2.6.3). После осреднения преобразованных таким образом уравнений движения и неразрывности получим уравнения Рейнольдса:
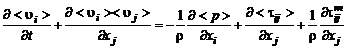 , (2.6.6)
, (2.6.6)
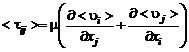 , (2.6.7)
, (2.6.7)
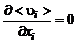 , (2.6.8)
, (2.6.8)
где через 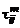 обозначен симметричный тензор добавочных напряжений, вызванных турбулентным переносом:
обозначен симметричный тензор добавочных напряжений, вызванных турбулентным переносом:
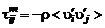 . (2.6.9)
. (2.6.9)
Шесть независимых компонентов тензора 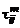 представляют собой шесть новых неизвестных.
представляют собой шесть новых неизвестных.
Система уравнений (2.6.6) – (2.6.9) не замкнута, поэтому для ее решения необходимо, на основании опытных данных или каким-либо другим образом, получить замыкающие соотношения, связывающие искомые параметры между собой. С момента составления Рейнольдсом его уравнений появилось множество полуэмпирических теорий, существо которых состоит в замыкании этих уравнений с помощью дополнительных соотношений. Для некоторых простых типов движения, например для пограничного слоя, замыкающие соотношения для отдельных составляющих турбулентного трения удалось подобрать. Эти результаты будут рассмотрены далее в разд. 3. Однако даже для простейшего случая – несжимаемой жидкости или газа – такие замыкающие соотношения, пригодные для всех видов течения, не получены. Интересно в этом отношении высказывание известного гидромеханика Лайтхилла, охарактеризовавшего современное состояние науки о турбулентности, как «кладбище теорий, на котором каждая новая теория добавляет еще одну могилу».
Рассмотренный способ построения уравнений движения легко обобщается на уравнения энергии и диффузии. Но это приводит к появлению новых неизвестных вида 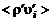 ,
, 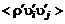 и т.д.
и т.д.



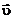 на составляющие:
на составляющие: 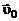 – скорость поступательного движения вместе с выбранным центром – точкой О,
– скорость поступательного движения вместе с выбранным центром – точкой О, 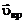 – скорость вращательного движения относительно этого центра и
– скорость вращательного движения относительно этого центра и 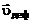 – скорость деформационного движения, т.е.
– скорость деформационного движения, т.е.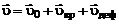 . (2.3.1)
. (2.3.1) .
.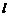 плоской площадки
плоской площадки 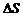 , перпендикулярной этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю:
, перпендикулярной этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю: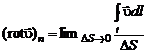 . (2.3.2)
. (2.3.2)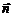 к площадке направляется так, чтобы при вычислении циркуляции обход по контуру
к площадке направляется так, чтобы при вычислении циркуляции обход по контуру 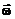 связаны простым соотношением
связаны простым соотношением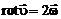 . (2.3.3)
. (2.3.3)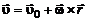 , (2.3.4)
, (2.3.4) обозначено векторное произведение, то
обозначено векторное произведение, то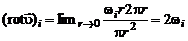 , (2.3.5)
, (2.3.5)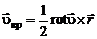 . (2.3.6)
. (2.3.6)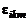 (каждый из индексов меняется от 1 до 3). Зададим эти числа следующим образом:
(каждый из индексов меняется от 1 до 3). Зададим эти числа следующим образом: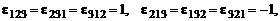 (2.3.7)
(2.3.7)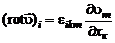 . (2.3.8)
. (2.3.8)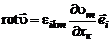 . (2.3.9)
. (2.3.9)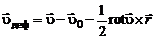 . (2.3.10)
. (2.3.10)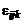 для записи векторного произведения в проекциях на оси координат:
для записи векторного произведения в проекциях на оси координат: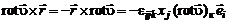 (2.3.11)
(2.3.11)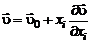 , (2.3.12)
, (2.3.12)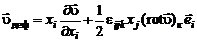 , (2.3.13)
, (2.3.13)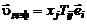 , (2.3.14)
, (2.3.14)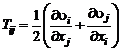 . (2.3.15)
. (2.3.15) можно составить таблицу из девяти величин, называемую тензором скоростей деформации.
можно составить таблицу из девяти величин, называемую тензором скоростей деформации.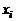 и
и 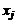 . Их взаимное расположение характеризуется таблицей направляющих косинусов
. Их взаимное расположение характеризуется таблицей направляющих косинусов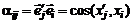 , (2.3.16)
, (2.3.16)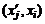 – угол между ортами осей. Так как скалярное произведение не зависит от порядка сомножителей, то очевидно, что
– угол между ортами осей. Так как скалярное произведение не зависит от порядка сомножителей, то очевидно, что 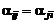 .
.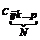 , где каждый индекс принимает значения от 1 до 3, и если элементы этой таблицы при переходе от одной системы координат к другой преобразуются по формулам
, где каждый индекс принимает значения от 1 до 3, и если элементы этой таблицы при переходе от одной системы координат к другой преобразуются по формулам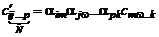 , (2.3.17)
, (2.3.17)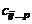 образует аффинный ортогональный тензор ранга N.
образует аффинный ортогональный тензор ранга N.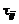 линейно зависят от элементов тензора скоростей деформа-
линейно зависят от элементов тензора скоростей деформа- :
: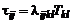 , (2.3.18)
, (2.3.18)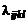 – тензор четвертого ранга, описывающий свойства среды.
– тензор четвертого ранга, описывающий свойства среды.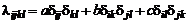 , (2.3.19)
, (2.3.19)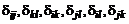 – единичные тензоры второго ранга.
– единичные тензоры второго ранга.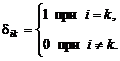 (2.3.20)
(2.3.20)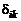 , называемый также символом Кронекера, обладает свойством изотропности.
, называемый также символом Кронекера, обладает свойством изотропности.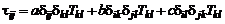 ,
,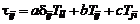 . (2.3.21)
. (2.3.21)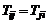 (см. формулу (2.3.15)), то, обозначая
(см. формулу (2.3.15)), то, обозначая 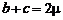 и
и 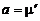 , получим обобщенный закон Ньютона:
, получим обобщенный закон Ньютона: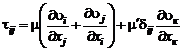 , (2.3.22)
, (2.3.22)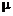 – коэффициент динамической вязкости.
– коэффициент динамической вязкости.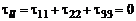 . (2.3.23)
. (2.3.23)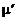 :
: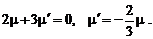 (2.3.24)
(2.3.24)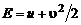 , (2.4.1)
, (2.4.1) – кинетическая энергия единицы массы газа;
– кинетическая энергия единицы массы газа; , (2.4.2)
, (2.4.2)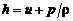 – теплосодержание (энтальпия) единицы массы газа;
– теплосодержание (энтальпия) единицы массы газа;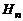 – обобщенное полное теплосодержание (энтальпия) с учетом стандартной теплоты образования и теплоты фазовых и полиморфных превращений:
– обобщенное полное теплосодержание (энтальпия) с учетом стандартной теплоты образования и теплоты фазовых и полиморфных превращений: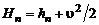 , (2.4.3)
, (2.4.3)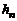 – обобщенное теплосодержание (энтальпия) с учетом стандартной теплоты образования и теплоты фазовых и полиморфных превращений. Значение
– обобщенное теплосодержание (энтальпия) с учетом стандартной теплоты образования и теплоты фазовых и полиморфных превращений. Значение 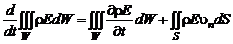 . (2.4.4)
. (2.4.4)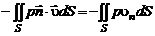 – мощность сил давления;
– мощность сил давления;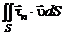 – мощность сил трения;
– мощность сил трения;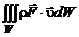 – мощность массовых сил,
– мощность массовых сил,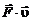 – скалярное произведение векторов
– скалярное произведение векторов 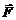 и
и 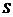 , и тепла, излучаемого или поглощаемого выделенной массой газа.
, и тепла, излучаемого или поглощаемого выделенной массой газа. вектор потока тепла, проходящего через единичную площадку в единицу времени. Тогда через граничную поверхность
вектор потока тепла, проходящего через единичную площадку в единицу времени. Тогда через граничную поверхность 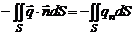 ,
,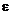 количество тепла, поступающего от окружающей среды к единице массы газа в единицу времени. В величину
количество тепла, поступающего от окружающей среды к единице массы газа в единицу времени. В величину 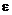 , в частности, может быть включена химическая энергия, выделяющаяся при прохождении химических реакций между компонентами смеси. Однако если вместо теплосодержания h использовать обобщенное теплосодержание
, в частности, может быть включена химическая энергия, выделяющаяся при прохождении химических реакций между компонентами смеси. Однако если вместо теплосодержания h использовать обобщенное теплосодержание 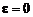 , так как значение
, так как значение 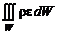 .
.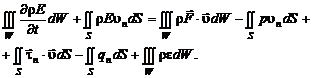 (2.4.5)
(2.4.5)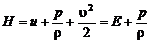 . (2.4.6)
. (2.4.6)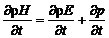 , (2.4.7)
, (2.4.7)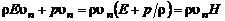 . (2.4.8)
. (2.4.8)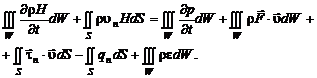 (2.4.9)
(2.4.9)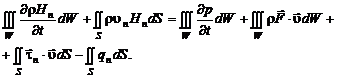 (2.4.10)
(2.4.10)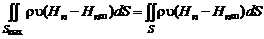 , (2.4.11)
, (2.4.11)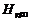 – обобщенное теплосодержание единицы массы газа окружающей среды.
– обобщенное теплосодержание единицы массы газа окружающей среды.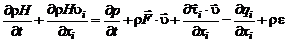 . (2.4.12)
. (2.4.12)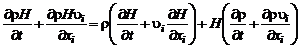 .
.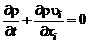 , (2.4.13)
, (2.4.13)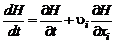 , (2.4.14)
, (2.4.14)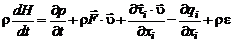 . (2.4.15)
. (2.4.15) .
.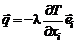 , (2.4.16)
, (2.4.16) – коэффициент теплопроводности.
– коэффициент теплопроводности.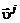 , определив ее как математическое ожидание скорости молекул j -го сорта. Тогда среднемассовая скорость жидкой частицы будет равна (см. формулу (2.1.3)):
, определив ее как математическое ожидание скорости молекул j -го сорта. Тогда среднемассовая скорость жидкой частицы будет равна (см. формулу (2.1.3)):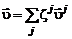 ;
;  , (2.4.17)
, (2.4.17) (2.4.18)
(2.4.18) – при смешении без химических реакций между компонентами либо в более общем виде
– при смешении без химических реакций между компонентами либо в более общем виде 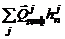 – если смешение может сопровождаться химическими реакциями.
– если смешение может сопровождаться химическими реакциями.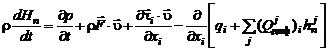 . (2.4.19)
. (2.4.19)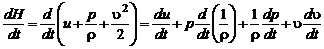 . (2.4.20)
. (2.4.20)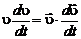 . (2.4.21)
. (2.4.21)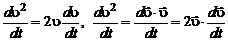 (2.4.22)
(2.4.22)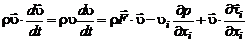 (2.4.23)
(2.4.23)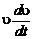 в (2.4.20). Получим
в (2.4.20). Получим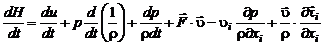 . (2.4.24)
. (2.4.24)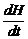 в левой части (2.4.15) ее выражением с помощью равенства (2.4.24), получим
в левой части (2.4.15) ее выражением с помощью равенства (2.4.24), получим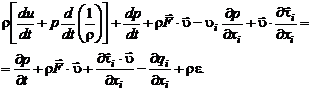 (2.4.25)
(2.4.25)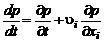 (2.4.26)
(2.4.26)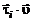
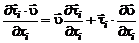 , (2.4.27)
, (2.4.27)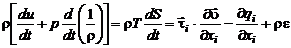 . (2.4.28)
. (2.4.28)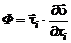 всегда положительна или равна нулю. Это позволяет судить о направлении процесса и сформулировать второе начало термодинамики: в теплоизолированной системе энтропия S либо возрастает, либо остается постоянной
всегда положительна или равна нулю. Это позволяет судить о направлении процесса и сформулировать второе начало термодинамики: в теплоизолированной системе энтропия S либо возрастает, либо остается постоянной 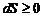 .
.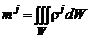 – масса j -го компонента, заключенного в момент времени t внутри произвольно выбранного объема W;
– масса j -го компонента, заключенного в момент времени t внутри произвольно выбранного объема W; – масса j -го компонента, который образуется в единицу времени в единице объема вследствие химических реакций;
– масса j -го компонента, который образуется в единицу времени в единице объема вследствие химических реакций;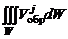 – масса j -го компоненты, который образуется в единицу времени внутри произвольно выбранного объема вследствие химических реакций.
– масса j -го компоненты, который образуется в единицу времени внутри произвольно выбранного объема вследствие химических реакций.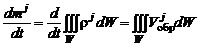 . (2.5.1)
. (2.5.1)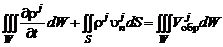 . (2.5.2)
. (2.5.2)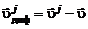 . (2.5.3)
. (2.5.3)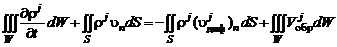 . (2.5.4)
. (2.5.4)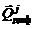 (см. (2.4.18)), то получим уравнение диффузии в интегральной форме:
(см. (2.4.18)), то получим уравнение диффузии в интегральной форме: . (2.5.5)
. (2.5.5)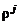 , а безразмерными массовыми концентрациями
, а безразмерными массовыми концентрациями 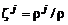 . Заменяя в (2.5.5) значение
. Заменяя в (2.5.5) значение 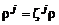 , приведем уравнение диффузии к виду
, приведем уравнение диффузии к виду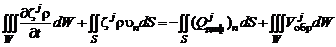 . (2.5.6)
. (2.5.6)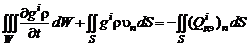 , (2.5.7)
, (2.5.7)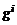 – массовая доля i -го элемента в смеси,
– массовая доля i -го элемента в смеси, 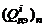 – проекция на внешнюю нормаль вектора потока диффузии i -го химического элемента:
– проекция на внешнюю нормаль вектора потока диффузии i -го химического элемента: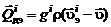 , (2.5.8)
, (2.5.8)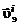 – математическое ожидание скорости i -го элемента.
– математическое ожидание скорости i -го элемента.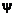 – массовой долей в смеси вещества, истекающего из сопл двигателя, – определить с помощью формул (1.1.12), (1.1.14), (1.1.16) химический состав смеси;
– массовой долей в смеси вещества, истекающего из сопл двигателя, – определить с помощью формул (1.1.12), (1.1.14), (1.1.16) химический состав смеси;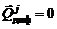 и
и 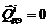 .
.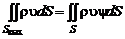 . (2.5.9)
. (2.5.9)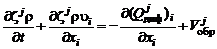 . (2.5.10)
. (2.5.10)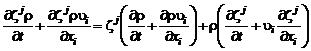 . (2.5.11)
. (2.5.11)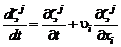 , (2.5.13)
, (2.5.13)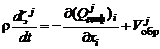 . (2.5.14)
. (2.5.14)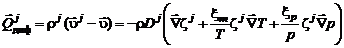 , (2.5.15)
, (2.5.15)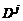 – коэффициент диффузии, определяющий диффузионный поток при наличии только градиента концентрации компонентов смеси
– коэффициент диффузии, определяющий диффузионный поток при наличии только градиента концентрации компонентов смеси 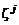 , а
, а 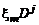 и
и 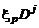 – коэффициенты термодиффузии и бародиффузии, которые определяют соответственно диффузионные потоки, возникающие вследствие градиентов температуры и давления, общих для всех компонентов смеси.
– коэффициенты термодиффузии и бародиффузии, которые определяют соответственно диффузионные потоки, возникающие вследствие градиентов температуры и давления, общих для всех компонентов смеси. , массовые силы пренебрежимо малыми, а коэффициент динамической вязкости
, массовые силы пренебрежимо малыми, а коэффициент динамической вязкости 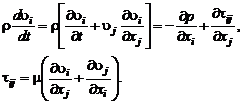 (2.6.1)
(2.6.1)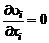 . (2.6.2)
. (2.6.2)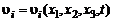 и
и 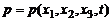 . Казалось бы, имея мощную вычислительную технику, мы без особого труда можем во всех случаях решить уравнения (2.6.1), (2.6.2) численными методами, например методом конечных разностей. Однако в действительности все намного сложнее.
. Казалось бы, имея мощную вычислительную технику, мы без особого труда можем во всех случаях решить уравнения (2.6.1), (2.6.2) численными методами, например методом конечных разностей. Однако в действительности все намного сложнее.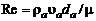 (
(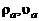 и
и 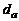 для изобарического участка струи – соответственно плотность, скорость и диаметр струи в начальном сечении) некоторых критических значений становится неустойчивым относительно малых возмущений. В результате потери устойчивости траектории жидких частиц приобретают запутанный, извилистый характер – движение из ламинарного становится турбулентным. Именно с турбулентными течениями мы чаще всего сталкиваемся на практике.
для изобарического участка струи – соответственно плотность, скорость и диаметр струи в начальном сечении) некоторых критических значений становится неустойчивым относительно малых возмущений. В результате потери устойчивости траектории жидких частиц приобретают запутанный, извилистый характер – движение из ламинарного становится турбулентным. Именно с турбулентными течениями мы чаще всего сталкиваемся на практике.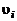 и р. Более подробный анализ показывает, что такой путь может быть реализован только при малых турбулентных числах Рейнольдса. Дело в том, что для адекватного описания течения конечноразностными уравнениями, заменяющими исходные дифференциальные уравнения в частных производных, приходится при турбулентном режиме дробить область течения на очень малые ячейки, размеры которых должны быть порядка самых малых размеров турбулентных вихрей. Сделанные оценки показали, что возможности даже самых мощных вычислительных машин пока недостаточны, чтобы обеспечить при этом требуемые объемы памяти и нужное быстродействие. С развитием вычислительной техники следует ожидать более широкого использования этих методов. Однако обсуждение этого вопроса выходит за рамки данного пособия.
и р. Более подробный анализ показывает, что такой путь может быть реализован только при малых турбулентных числах Рейнольдса. Дело в том, что для адекватного описания течения конечноразностными уравнениями, заменяющими исходные дифференциальные уравнения в частных производных, приходится при турбулентном режиме дробить область течения на очень малые ячейки, размеры которых должны быть порядка самых малых размеров турбулентных вихрей. Сделанные оценки показали, что возможности даже самых мощных вычислительных машин пока недостаточны, чтобы обеспечить при этом требуемые объемы памяти и нужное быстродействие. С развитием вычислительной техники следует ожидать более широкого использования этих методов. Однако обсуждение этого вопроса выходит за рамки данного пособия.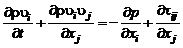 . (2.6.3)
. (2.6.3)
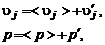 (2.6.4)
(2.6.4)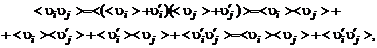 (2.6.5)
(2.6.5) обозначено среднее значение случайной величины, а штрихом вверху – ее пульсационная составляющая. Подставим (2.6.4) в (2.6.1) – (2.6.3). После осреднения преобразованных таким образом уравнений движения и неразрывности получим уравнения Рейнольдса:
обозначено среднее значение случайной величины, а штрихом вверху – ее пульсационная составляющая. Подставим (2.6.4) в (2.6.1) – (2.6.3). После осреднения преобразованных таким образом уравнений движения и неразрывности получим уравнения Рейнольдса: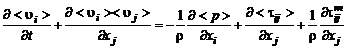 , (2.6.6)
, (2.6.6)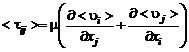 , (2.6.7)
, (2.6.7)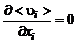 , (2.6.8)
, (2.6.8)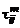 обозначен симметричный тензор добавочных напряжений, вызванных турбулентным переносом:
обозначен симметричный тензор добавочных напряжений, вызванных турбулентным переносом: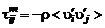 . (2.6.9)
. (2.6.9)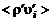 ,
, 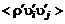 и т.д.
и т.д.


