Если для дифференциального уравнения  выполнено условие
выполнено условие  =
= 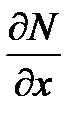 , его называют уравнением в полных дифференциалах: в этом случае существует функция
, его называют уравнением в полных дифференциалах: в этом случае существует функция  , для которой выражение
, для которой выражение  является ее полным дифференциалом. Так как полный дифференциал функции имеет вид
является ее полным дифференциалом. Так как полный дифференциал функции имеет вид  , то должны выполняться равенства
, то должны выполняться равенства  и
и  . Если функция
. Если функция  найдена, то равенство
найдена, то равенство 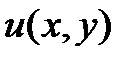 =
=  , где
, где  − произвольная постоянная величина, задает семейство решений дифференциального уравнения в полных дифференциалах.
− произвольная постоянная величина, задает семейство решений дифференциального уравнения в полных дифференциалах.
Для нахождения функции  используют стандартный алгоритм, который иллюстрирует приведённый ниже пример.
используют стандартный алгоритм, который иллюстрирует приведённый ниже пример.
Пример 1.6. Решить уравнение  , предварительно удостоверившись, что заданное дифференциальное уравнение является уравнением в полных дифференциалах.
, предварительно удостоверившись, что заданное дифференциальное уравнение является уравнением в полных дифференциалах.
Решение. 1) Вычислим производные  =3 и
=3 и  =3. Равенство
=3. Равенство  =
=  подтверждено, это значит, что заданное уравнение есть уравнение в полных дифференциалах.
подтверждено, это значит, что заданное уравнение есть уравнение в полных дифференциалах.
2) Учитывая, что  , вычислим
, вычислим  =
=  +
+  . В нашем случае имеем:
. В нашем случае имеем:
 =
=  +
+  =
=  +
+  . (1.7)
. (1.7)
3) Вычислим производную 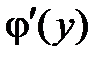 =
=  –
– 
 . В нашем случае, учитывая заданное уравнением выражение
. В нашем случае, учитывая заданное уравнением выражение  и (1.7), получаем
и (1.7), получаем  =
=  .
.
4) Интегрируя, находим функцию  =
=  =
=  .
.
5) Подставляя  в (1.7), записываем общее решение заданного уравнения
в (1.7), записываем общее решение заданного уравнения
 =
=  +
+  =
= 
 =
=  .
.
Ответ.  =
= 
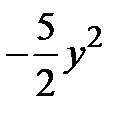 =
=  .
.
Задание 1.6. Решить уравнение, предварительно проверив, что заданное дифференциальное уравнение является уравнением в полных дифференциалах.
| Вар.
| Уравнение:
| Вар.
| Уравнение:
|
| 1.6.1.
| 
| 1.6.16.
| 
|
| 1.6.2.
| 
| 1.6.17.
| 
|
| 1.6.3.
| 
| 1.6.18.
| 
|
| 1.6.4.
| 
| 1.6.19.
| 
|
| 1.6.5.
| 
| 1.6.20.
| 
|
| 1.6.6.
| 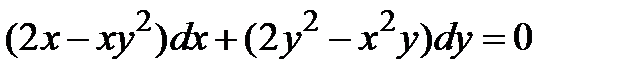
| 1.6.21.
| 
|
| 1.6.7.
| 
| 1.6.22.
| 
|
| 1.6.8.
| 
| 1.6.23.
| 
|
| 1.6.9.
| 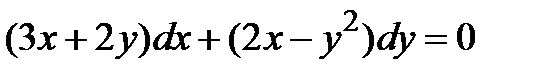
| 1.6.24.
| 
|
| 1.6.10.
| 
| 1.6.25.
| 
|
| 1.6.11.
| 
| 1.6.26.
| 
|
| 1.6.12.
| 
| 1.6.27.
| 
|
| 1.6.13.
| 
| 1.6.28.
| 
|
| 1.6.14.
| 
| 1.6.29.
| 
|
| 1.6.15.
| 
| 1.6.30.
| 
|
1.7. Нахождение уравнений кривых с помощью дифференциальных
уравнений 1-го порядка
Для нахождения уравнений кривых с помощью дифференциальных уравнений 1-го порядка по заданным геометрическим свойствам кривых составляют уравнение  , связывающее координаты произвольной точки
, связывающее координаты произвольной точки  кривой
кривой  и производную функции
и производную функции  . Напомним, что геометрический смысл производной
. Напомним, что геометрический смысл производной  − тангенс угла наклона касательной к кривой
− тангенс угла наклона касательной к кривой  в точке
в точке  .
.
На рисунке 1.1 представлена некоторая кривая  . Для произвольной точки
. Для произвольной точки  этой кривой построены касательная
этой кривой построены касательная  и нормаль
и нормаль  и выделены точки пересечения касательной и нормали с осями
и выделены точки пересечения касательной и нормали с осями  и
и  , именно: а) для касательной – точки
, именно: а) для касательной – точки  и
и  ; б) для нормали – точки
; б) для нормали – точки  и
и  .
.

Геометрические свойства кривой обычно задаются условиями на соотношения между длинами отрезков

,

,

,

,

,

,

и
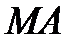
– отрезки касательной,

– подкасательная,

и

– отрезки нормали,

– поднормаль (см.рис.1.1). Каждое такое соотношение есть дифференциальное уравнение, определяющее совокупные геометрические свойства кривой. Решая уравнение, находят соответствующее семейство кривых с заданными свойствами. Задавая начальные условия, из семейства кривых выделяют единственную кривую.
Ниже приведены формулы длин основных характерных отрезков кривой 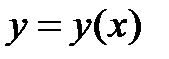
 ,
,  ,
,  ,
,  ,
,  ,
,  Величиной
Величиной  обозначен угловой коэффициент касательной в точке
обозначен угловой коэффициент касательной в точке  .
.
Запишем для точки  уравнение касательной
уравнение касательной
 (1.8)
(1.8)
и нормали
 . (1.9)
. (1.9)
Используя (1.8), определим координаты точек  и
и  пересечения касательной с осями координат
пересечения касательной с осями координат  ,
,  и вычислим длины отрезков
и вычислим длины отрезков 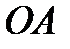 ,
,  :
:
а) для точки  имеем:
имеем:
 =0 →
=0 →  =
=  →
→  =
=  →
→  =
=  ; (1.10)
; (1.10)
б) для точки  имеем:
имеем:
 =0 →
=0 →  =
=  →
→  =
=  →
→  =
= 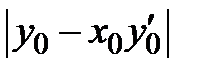 . (1.11)
. (1.11)
Зная координаты точки  (см. (1.10)), вычислим длину подкасательной:
(см. (1.10)), вычислим длину подкасательной:
 =
= 
Аналогично, используя (1.9), найдем координаты точек  и
и  пересечения нормали с осями координат
пересечения нормали с осями координат  ,
,  и вычислим длины отрезков
и вычислим длины отрезков  ,
,  :
:
а) для точки  имеем:
имеем:
 =0 →
=0 →  =
=  →
→  =
=  →
→  =
=  ; (1.12)
; (1.12)
б) для точки 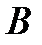 имеем:
имеем:
 =0 →
=0 →  =
= 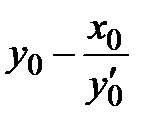 →
→  =
=  →
→  =
=  .
.
Используя (1.12), вычислим длину поднормали  =
=  .
.
 Пример 1.7.
Пример 1.7. Найти уравнения кривых, проходящих через точку (1,1), зная, что длина отрезка, отсекаемого на оси ординат касательной к кривой в каждой точке, пропорциональна ординате точки касания. Принять коэффициент пропорциональности

=2.
Решение. Пусть  – произвольная точка кривой
– произвольная точка кривой  (см.рис.1.2). Считаем
(см.рис.1.2). Считаем 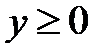 , так как ордината должна быть пропорциональна неотрицательной величине – длине отрезка. Условие задачи означает, что длина отрезка
, так как ордината должна быть пропорциональна неотрицательной величине – длине отрезка. Условие задачи означает, что длина отрезка 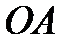 равна 2
равна 2  , то есть, применяя формулу (1.11) для вычисления длины отрезка
, то есть, применяя формулу (1.11) для вычисления длины отрезка 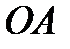 ,
,  =2
=2  .
.
Из равенства  =2
=2  следует, что необходимо рассмотреть два случая:
следует, что необходимо рассмотреть два случая:
▪ Случай-1:  ; (1.13)
; (1.13)
▪ Случай-2:  . (1.14)
. (1.14)
Случай-1.
1) Дифференциальное уравнение (1.13) имеет решением функцию  , график которой не проходит через точку (1,1).
, график которой не проходит через точку (1,1).

2) Запишем уравнение (1.13) в виде
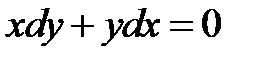
– это уравнение с разделяющимися переменными, общим решением которого является семейство гипербол

. Требование

означает если

, то

, если

, то

(см.рис.1.3). Точка

выделяет из семейства гипербол единственную кривую.
Случай-2.

1) Перепишем уравнение (1.14) в виде

. Нетрудно получить его общее решение

– семейство кубических парабол. Здесь также если

, то

, если

, то

.Кубическая парабола

проходит через точку

при

=1 (см.рис.1.4; для значений

семейство интегральных кривых не показано).
Ответ.  ,
,  .
.
Задание 1.7. Найти уравнения кривых.
Замечания. 1) При оформлении решений заданий изобразите на рисунке 3-4 кривые из семейства, соответствующих общему решению дифференциального уравнения, и среди них выделите частное решение: линию, проходящую через заданную точку.
2) Используя кривую частного решения, покажите на чертеже касательную и подкасательную, нормаль и поднормаль для заданной точки  .
.
1.7.1. Найти уравнение линии, проходящей через точку 
 , зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания:
, зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания:  .
.
1.7.2. Найти уравнение линии, проходящей через точку 
 , зная, что угловой коэффициент её касательной в этой точке равен абсциссе точки касания, умноженной на 2.
, зная, что угловой коэффициент её касательной в этой точке равен абсциссе точки касания, умноженной на 2.
1.7.3. Найти уравнение линии, проходящей через точку 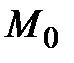
 , зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой  .
.
1.7.4. Найти уравнение линии, проходящей через точку 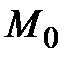
 , зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания. Рассмотреть только случай, когда в каждой точке кривой  .
.
1.7.5. Найти уравнение линии, проходящей через точку 
 , зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой  .
.
1.7.6. Найти уравнение линии, проходящей через точку 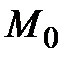
 , зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания
, зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания 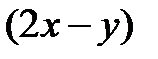 .
.
1.7.7. Найти уравнение линии, проходящей через точку 
 , зная, что угловой коэффициент её касательной в этой точке равен абсциссе точки касания, умноженной на 4.
, зная, что угловой коэффициент её касательной в этой точке равен абсциссе точки касания, умноженной на 4.
1.7.8. Найти уравнение линии, проходящей через точку 
 , зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой  .
.
1.7.9. Найти уравнение линии, проходящей через точку 
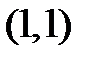 , зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания. Рассмотреть только случай, когда в каждой точке кривой  .
.
1.7.10. Найти уравнение линии, проходящей через точку 
 , зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой  .
.
1.7.11. Найти уравнение линии, проходящей через точку 
 , зная, что длина её поднормали для каждой точки кривой равна ординате точки касания. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её поднормали для каждой точки кривой равна ординате точки касания. Рассмотреть только случай, когда в каждой точке кривой  .
.
1.7.12. Найти уравнение линии, проходящей через точку 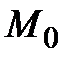
 , зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания
, зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания  .
.
1.7.13. Найти уравнение линии, проходящей через точку 
 , зная, что угловой коэффициент её касательной в этой точке равен абсциссе точки касания, умноженной на −2.
, зная, что угловой коэффициент её касательной в этой точке равен абсциссе точки касания, умноженной на −2.
1.7.14. Найти уравнение линии, проходящей через точку 
 , зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой  .
.
1.7.15. Найти уравнение линии, проходящей через точку 
 , зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой  .
.
1.7.16. Найти уравнение линии, проходящей через точку 
 , зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой  .
.
1.7.17. Найти уравнение линии, проходящей через точку 
 , зная, что длина её поднормали для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её поднормали для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой  .
.
1.7.18. Найти уравнение линии, проходящей через точку 
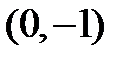 , зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания
, зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания  .
.
1.7.19. Найти уравнение линии, проходящей через точку 
 , зная, что угловой коэффициент её касательной в этой точке равен ординате точки касания, умноженной на 2.
, зная, что угловой коэффициент её касательной в этой точке равен ординате точки касания, умноженной на 2.
1.7.20. Найти уравнение линии, проходящей через точку 
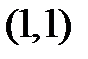 , зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой  .
.
1.7.21. Найти уравнение линии, проходящей через точку 
 , зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой  .
.
1.7.22. Найти уравнение линии, проходящей через точку 
 , зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой  .
.
1.7.23. Найти уравнение линии, проходящей через точку 
 , зная, что длина её поднормали для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её поднормали для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой  .
.
1.7.24. Найти уравнение линии, проходящей через точку 
 , зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания
, зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания  .
.
1.7.25. Найти уравнение линии, проходящей через точку 
 , зная, что угловой коэффициент её касательной в этой точке равен ординате точки касания, умноженной на −2.
, зная, что угловой коэффициент её касательной в этой точке равен ординате точки касания, умноженной на −2.
1.7.26. Найти уравнение линии, проходящей через точку 
 , зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания, умноженной на −2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания, умноженной на −2. Рассмотреть только случай, когда в каждой точке кривой  .
.
1.7.27. Найти уравнение линии, проходящей через точку 
 , зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой  .
.
1.7.28. Найти уравнение линии, проходящей через точку 
 , зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания, умноженной на −2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания, умноженной на −2. Рассмотреть только случай, когда в каждой точке кривой  .
.
1.7.29. Найти уравнение линии, проходящей через точку 
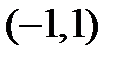 , зная, что длина её поднормали для каждой точки кривой равна ординате точки касания, умноженной на −2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её поднормали для каждой точки кривой равна ординате точки касания, умноженной на −2. Рассмотреть только случай, когда в каждой точке кривой  .
.
1.7.30. Найти уравнение линии, проходящей через точку 
 , зная, что угловой коэффициент её касательной в этой точке равен квадрату абсциссы точки касания, умноженной на 2.
, зная, что угловой коэффициент её касательной в этой точке равен квадрату абсциссы точки касания, умноженной на 2.
1.8. Применение дифференциальных уравнений 1-го порядка для
решения задач физики и химии
Для составления дифференциального уравнения – математической модели физической (химической) задачи – часто применяют следующие способы:
1) записывают условие на производную искомой величины, используя известные законы физики и физический смысл производной;
2) определяют, какая из величин будет независимой переменной (обозначим её x), а какая зависимой (обозначим её y); затем, используя соотношения между нужными величинами при постоянных значениях параметров, находят линейное приближение для приращения  когда независимая переменная получила приращение
когда независимая переменная получила приращение  ; разделив
; разделив  на
на  и переходя к пределу при
и переходя к пределу при  , получают дифференциальное уравнение.
, получают дифференциальное уравнение.
Для правильного составления уравнений требуется знание физических законов (первый и второй законы Ньютона, законы Кирхгофа для цепи переменного тока, закон Ньютона для скорости изменения температуры тела (см. указание 3 к заданию 1.8 и некоторые другие) в рамках стандартного курса общей физики по разделам: механика, термодинамика и молекулярная физика, электричество и магнетизм.
Справочный материал
Закон гравитации. Сила притяжения двух точечных (или сферически симметричных) масс 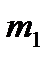 и
и  , находящихся на расстоянии
, находящихся на расстоянии  друг от друга:
друг от друга:
 ,
,
где  (в системе СИ) – гравитационная постоянная.
(в системе СИ) – гравитационная постоянная.



 выполнено условие
выполнено условие  =
= 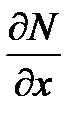 , его называют уравнением в полных дифференциалах: в этом случае существует функция
, его называют уравнением в полных дифференциалах: в этом случае существует функция  , для которой выражение
, для которой выражение  является ее полным дифференциалом. Так как полный дифференциал функции имеет вид
является ее полным дифференциалом. Так как полный дифференциал функции имеет вид  , то должны выполняться равенства
, то должны выполняться равенства  и
и  . Если функция
. Если функция  найдена, то равенство
найдена, то равенство 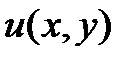 =
=  , где
, где  − произвольная постоянная величина, задает семейство решений дифференциального уравнения в полных дифференциалах.
− произвольная постоянная величина, задает семейство решений дифференциального уравнения в полных дифференциалах. используют стандартный алгоритм, который иллюстрирует приведённый ниже пример.
используют стандартный алгоритм, который иллюстрирует приведённый ниже пример. , предварительно удостоверившись, что заданное дифференциальное уравнение является уравнением в полных дифференциалах.
, предварительно удостоверившись, что заданное дифференциальное уравнение является уравнением в полных дифференциалах. =3 и
=3 и  =3. Равенство
=3. Равенство  =
=  подтверждено, это значит, что заданное уравнение есть уравнение в полных дифференциалах.
подтверждено, это значит, что заданное уравнение есть уравнение в полных дифференциалах. , вычислим
, вычислим  =
=  +
+  . В нашем случае имеем:
. В нашем случае имеем: =
=  +
+  =
=  +
+  . (1.7)
. (1.7)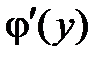 =
=  –
– 
 . В нашем случае, учитывая заданное уравнением выражение
. В нашем случае, учитывая заданное уравнением выражение  и (1.7), получаем
и (1.7), получаем  =
=  .
. =
=  =
=  .
. в (1.7), записываем общее решение заданного уравнения
в (1.7), записываем общее решение заданного уравнения =
=  +
+  =
= 
 =
=  .
. =
= 
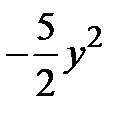 =
=  .
.









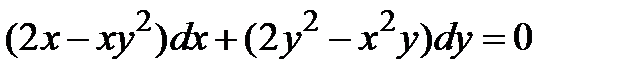





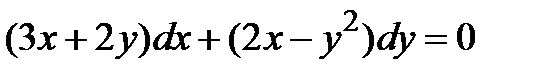













 , связывающее координаты произвольной точки
, связывающее координаты произвольной точки  кривой
кривой  и производную функции
и производную функции  . Напомним, что геометрический смысл производной
. Напомним, что геометрический смысл производной  − тангенс угла наклона касательной к кривой
− тангенс угла наклона касательной к кривой  в точке
в точке  .
. . Для произвольной точки
. Для произвольной точки  этой кривой построены касательная
этой кривой построены касательная  и нормаль
и нормаль  и выделены точки пересечения касательной и нормали с осями
и выделены точки пересечения касательной и нормали с осями  и
и  , именно: а) для касательной – точки
, именно: а) для касательной – точки  и
и  ; б) для нормали – точки
; б) для нормали – точки  и
и  .
. Геометрические свойства кривой обычно задаются условиями на соотношения между длинами отрезков
Геометрические свойства кривой обычно задаются условиями на соотношения между длинами отрезков  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  и
и 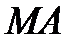 – отрезки касательной,
– отрезки касательной,  – подкасательная,
– подкасательная,  и
и  – отрезки нормали,
– отрезки нормали,  – поднормаль (см.рис.1.1). Каждое такое соотношение есть дифференциальное уравнение, определяющее совокупные геометрические свойства кривой. Решая уравнение, находят соответствующее семейство кривых с заданными свойствами. Задавая начальные условия, из семейства кривых выделяют единственную кривую.
– поднормаль (см.рис.1.1). Каждое такое соотношение есть дифференциальное уравнение, определяющее совокупные геометрические свойства кривой. Решая уравнение, находят соответствующее семейство кривых с заданными свойствами. Задавая начальные условия, из семейства кривых выделяют единственную кривую.
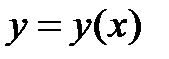
 ,
,  ,
,  ,
,  ,
,  ,
,  Величиной
Величиной  обозначен угловой коэффициент касательной в точке
обозначен угловой коэффициент касательной в точке  .
. уравнение касательной
уравнение касательной (1.8)
(1.8) . (1.9)
. (1.9) и
и  пересечения касательной с осями координат
пересечения касательной с осями координат  ,
,  и вычислим длины отрезков
и вычислим длины отрезков 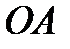 ,
,  :
: имеем:
имеем: =0 →
=0 →  =
=  →
→  =
=  →
→  =
=  ; (1.10)
; (1.10) имеем:
имеем: =0 →
=0 →  =
=  →
→  =
=  →
→  =
= 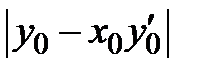 . (1.11)
. (1.11) =
= 
 и
и  пересечения нормали с осями координат
пересечения нормали с осями координат  ,
,  и вычислим длины отрезков
и вычислим длины отрезков  ,
,  :
: имеем:
имеем: =0 →
=0 →  =
=  →
→  =
=  →
→  =
=  ; (1.12)
; (1.12)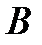 имеем:
имеем: =0 →
=0 →  =
= 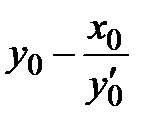 →
→  =
=  →
→  =
=  .
. =
=  .
. Пример 1.7. Найти уравнения кривых, проходящих через точку (1,1), зная, что длина отрезка, отсекаемого на оси ординат касательной к кривой в каждой точке, пропорциональна ординате точки касания. Принять коэффициент пропорциональности
Пример 1.7. Найти уравнения кривых, проходящих через точку (1,1), зная, что длина отрезка, отсекаемого на оси ординат касательной к кривой в каждой точке, пропорциональна ординате точки касания. Принять коэффициент пропорциональности  =2.
=2. – произвольная точка кривой
– произвольная точка кривой  (см.рис.1.2). Считаем
(см.рис.1.2). Считаем 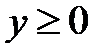 , так как ордината должна быть пропорциональна неотрицательной величине – длине отрезка. Условие задачи означает, что длина отрезка
, так как ордината должна быть пропорциональна неотрицательной величине – длине отрезка. Условие задачи означает, что длина отрезка 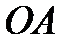 равна 2
равна 2  , то есть, применяя формулу (1.11) для вычисления длины отрезка
, то есть, применяя формулу (1.11) для вычисления длины отрезка 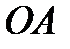 ,
,  =2
=2  .
. =2
=2  следует, что необходимо рассмотреть два случая:
следует, что необходимо рассмотреть два случая: ; (1.13)
; (1.13) . (1.14)
. (1.14) , график которой не проходит через точку (1,1).
, график которой не проходит через точку (1,1). 2) Запишем уравнение (1.13) в виде
2) Запишем уравнение (1.13) в виде 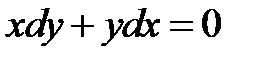 – это уравнение с разделяющимися переменными, общим решением которого является семейство гипербол
– это уравнение с разделяющимися переменными, общим решением которого является семейство гипербол  . Требование
. Требование  означает если
означает если  , то
, то  , если
, если  , то
, то  (см.рис.1.3). Точка
(см.рис.1.3). Точка  выделяет из семейства гипербол единственную кривую.
выделяет из семейства гипербол единственную кривую.
 1) Перепишем уравнение (1.14) в виде
1) Перепишем уравнение (1.14) в виде  . Нетрудно получить его общее решение
. Нетрудно получить его общее решение  – семейство кубических парабол. Здесь также если
– семейство кубических парабол. Здесь также если  при
при  =1 (см.рис.1.4; для значений
=1 (см.рис.1.4; для значений  семейство интегральных кривых не показано).
семейство интегральных кривых не показано).
 ,
,  .
. .
.
 , зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания:
, зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания:  .
.
 , зная, что угловой коэффициент её касательной в этой точке равен абсциссе точки касания, умноженной на 2.
, зная, что угловой коэффициент её касательной в этой точке равен абсциссе точки касания, умноженной на 2.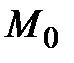
 , зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой  .
.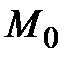
 , зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания. Рассмотреть только случай, когда в каждой точке кривой  .
.
 , зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой  .
.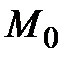
 , зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания
, зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания 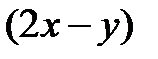 .
.
 , зная, что угловой коэффициент её касательной в этой точке равен абсциссе точки касания, умноженной на 4.
, зная, что угловой коэффициент её касательной в этой точке равен абсциссе точки касания, умноженной на 4.
 , зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой  .
.
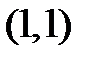 , зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания. Рассмотреть только случай, когда в каждой точке кривой  .
.
 , зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания. Рассмотреть только случай, когда в каждой точке кривой  .
.
 , зная, что длина её поднормали для каждой точки кривой равна ординате точки касания. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её поднормали для каждой точки кривой равна ординате точки касания. Рассмотреть только случай, когда в каждой точке кривой  .
.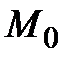
 , зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания
, зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания  .
.
 , зная, что угловой коэффициент её касательной в этой точке равен абсциссе точки касания, умноженной на −2.
, зная, что угловой коэффициент её касательной в этой точке равен абсциссе точки касания, умноженной на −2.
 , зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой  .
.
 , зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой  .
.
 , зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой  .
.
 , зная, что длина её поднормали для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её поднормали для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой  .
.
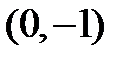 , зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания
, зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания  .
.
 , зная, что угловой коэффициент её касательной в этой точке равен ординате точки касания, умноженной на 2.
, зная, что угловой коэффициент её касательной в этой точке равен ординате точки касания, умноженной на 2.
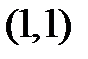 , зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой  .
.
 , зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой  .
.
 , зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой  .
.
 , зная, что длина её поднормали для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её поднормали для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой  .
.
 , зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания
, зная, что угловой коэффициент её касательной в этой точке равен линейной комбинации координат точки касания  .
.
 , зная, что угловой коэффициент её касательной в этой точке равен ординате точки касания, умноженной на −2.
, зная, что угловой коэффициент её касательной в этой точке равен ординате точки касания, умноженной на −2.
 , зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания, умноженной на −2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её подкасательной для каждой точки кривой равна абсциссе точки касания, умноженной на −2. Рассмотреть только случай, когда в каждой точке кривой  .
.
 , зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её подкасательной для каждой точки кривой равна ординате точки касания, умноженной на 2. Рассмотреть только случай, когда в каждой точке кривой  .
.
 , зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания, умноженной на −2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её поднормали для каждой точки кривой равна абсциссе точки касания, умноженной на −2. Рассмотреть только случай, когда в каждой точке кривой  .
.
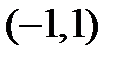 , зная, что длина её поднормали для каждой точки кривой равна ординате точки касания, умноженной на −2. Рассмотреть только случай, когда в каждой точке кривой
, зная, что длина её поднормали для каждой точки кривой равна ординате точки касания, умноженной на −2. Рассмотреть только случай, когда в каждой точке кривой  .
.
 , зная, что угловой коэффициент её касательной в этой точке равен квадрату абсциссы точки касания, умноженной на 2.
, зная, что угловой коэффициент её касательной в этой точке равен квадрату абсциссы точки касания, умноженной на 2. когда независимая переменная получила приращение
когда независимая переменная получила приращение  ; разделив
; разделив  , получают дифференциальное уравнение.
, получают дифференциальное уравнение.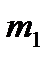 и
и  , находящихся на расстоянии
, находящихся на расстоянии  друг от друга:
друг от друга: ,
, (в системе СИ) – гравитационная постоянная.
(в системе СИ) – гравитационная постоянная.

