ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ
Момент силы F относительно точки есть вектор, равный
 ,
,
где r – радиус-вектор, проведенный из точки, относительно которой рассматривается момент силы F, к точке приложения силы.
Моментом нескольких сил относительно точки называется сумма моментов этих сил относительно той же точки.
Аналогично определяется момент импульса материальной точки относительно неподвижного начала:
 .
.
Момент силы и момент импульса связаны между собой соотношением, которое называется уравнением моментов:
 ,
,
где N – геометрическая сумма моментов внешних сил, действующих на систему материальных точек.
Если момент внешних сил относительно неподвижного начала равен нулю (N =0), то момент импульса системы относительно того же начала остается постоянным во времени (М =const) – закон сохранения момента импульса. В частности, момент импульса сохраняется для замкнутой системы материальных точек.
Моментами силы и импульса относительно произвольной оси называются проекции на эту ось их моментов относительно точки, лежащей на той же оси.
Моментом инерции системы относительно оси называется величина I, равная сумме произведений масс материальных точек на квадраты расстояний их до оси вращения:
 .
.
Если вещество в теле распределено непрерывно, то вычисление его момента инерции сводится к вычислению интеграла
 ,
,
где r – расстояние от элемента массы dm до оси вращения. Интегрирование должно производиться по всей массе тела.
Основное уравнение динамики вращательного движение вокруг неподвижной оси:
 ,
,
где ω – угловая скорость вращения. Оно напоминает уравнение Ньютона для движения материальной точки. Роль массы играет момент инерции I, роль скорости – угловая скорость ω, роль силы – момент силы N, роль импульса – момент импульса M=Iω. Момент импульса М часто называют вращательным импульсом системы. Если момент внешних сил относительно оси вращения равен нулю, то вращательный импульс Iω сохраняется.
Кинетическая энергия вращающегося твердого тела представляется в виде:
 .
.
Теорема Гюйгенса-Штейнера: момент инерции тела относительно какой-либо оси равен моменту инерции его относительно параллельной оси, проходящей через центр масс, сложенному с величиной ma2, где а –расстояние между осями
 .
.
Примеры решения задач.
1. Шайба A массы m, скользя по гладкой горизонтальной поверхности со скоростью v, испытала в точке О (рис.5.1) абсолютно упругий удар с гладкой неподвижной стенкой. Угол между направлением движения шайбы и нормалью к стенке равен a. Найти: а) точки, относительно которых момент импульса M шайбы остается постоянным в этом процессе; б) модуль приращения вектора момента импульса шайбы относительно точки О, которая находится в плоскости движения шайбы на расстоянии l от точки О.

Рис.5.1
Дано:
m,, l, α, v=const
____________________
 -?
-?
Решение:
В первом вопросе спрашивается, относительно каких точек момент импульса М остается постоянным. Из уравнения моментов  , где N – момент внешних сил относительно рассматриваемой точки, видно, что М =const, если момент сил N относительно этой точки равен нулю. В процессе движения шайбы ее скорость v=const, поэтому равнодействующая сил, действующих на нее, равна нулю и N =0. Но в момент удара о стенку на шайбу будет действовать сила реакции опоры Nоп . Выберем произвольную точку В и вычислим относительно нее момент сил:
, где N – момент внешних сил относительно рассматриваемой точки, видно, что М =const, если момент сил N относительно этой точки равен нулю. В процессе движения шайбы ее скорость v=const, поэтому равнодействующая сил, действующих на нее, равна нулю и N =0. Но в момент удара о стенку на шайбу будет действовать сила реакции опоры Nоп . Выберем произвольную точку В и вычислим относительно нее момент сил:
 .
.
Он будет равен нулю, если sinβ=0, или β=π. Т.о., М =const относительно точек прямой, перпендикулярной к стенке и проходящей через т.О.
Найдем приращение  Δ М = М 1- М, а затем его модуль. Момент импульса шайбы относительно точки О’ после удара о стенку(см.рисунок):
Δ М = М 1- М, а затем его модуль. Момент импульса шайбы относительно точки О’ после удара о стенку(см.рисунок):
 .
.
Вектор М 1 перпендикулярен плоскости, в которой движется шайба, и направлен от нас. По модулю 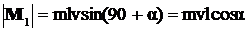 . Момент импульса шайбы относительно точки О до удара о стенку находится аналогично:
. Момент импульса шайбы относительно точки О до удара о стенку находится аналогично:  . Он также перпендикулярен плоскости, в которой движется шайба, но направлен от нас. По модулю
. Он также перпендикулярен плоскости, в которой движется шайба, но направлен от нас. По модулю  . Тогда приращение момента импульса Δ М = М 1- М= 2 М 1, а модуль приращения
. Тогда приращение момента импульса Δ М = М 1- М= 2 М 1, а модуль приращения  .
.
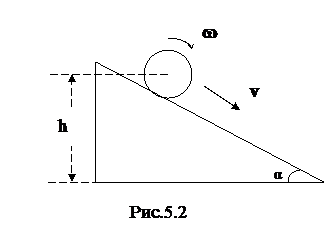
2. С наклонной плоскости, составляющей угол α = 300 с горизонтом, скатывается без скольжения шарик (рис.5.2). Пренебрегая трением, определить время движения шарика по наклонной плоскости, если известно, что его центр масс при скатывании понизился на h = 30 см.
| Дано:
α = 300
h = 30 см = 0,3м
_______________
t -?
| 
|
Решение:
Т.к. трения нет, воспользуемся законом сохранения механической энергии:
 ,
,
где  - кинетическая энергия поступательного движения шарика,
- кинетическая энергия поступательного движения шарика,  - кинетическая энергия вращательного движения шарика.
- кинетическая энергия вращательного движения шарика.  - момент инерции шарика относительно оси, проходящей через его центр,
- момент инерции шарика относительно оси, проходящей через его центр,  - угловая скорость вращения. Подставив все в закон сохранения энергии, найдем скорость поступательного движения шарика:
- угловая скорость вращения. Подставив все в закон сохранения энергии, найдем скорость поступательного движения шарика:
 .
.
Поскольку движение шарика равноускоренное, воспользуемся следующими формулами:
 .
.
Выразим время:
 .
.
Воспользовавшись полученным ранее выражением для скорости, получим:
 .
.
Подставив численные значения, имеем: t = 0,585 с.
СПИСОК ЗАДАЧ.
5.1. Шарик массы m бросили под углом 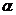 к горизонту с начальной скоростью v0. Найти модуль вектора момента импульса шарика относительно точки бросания в зависимости от времени движения. Вычислить M в вершине траектории, если m = 130 г,
к горизонту с начальной скоростью v0. Найти модуль вектора момента импульса шарика относительно точки бросания в зависимости от времени движения. Вычислить M в вершине траектории, если m = 130 г, 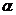 = 450 и v0 = 25 м/с. Сопротивлением воздуха пренебречь.
= 450 и v0 = 25 м/с. Сопротивлением воздуха пренебречь.
Ответ: M = (1/2)mgv0t2cosa; M = (mv03/2g) sin2acosa = 37 кг∙м2/с.
5.2. Момент импульса частицы относительно некоторой точки O меняетсясовременем по закону M = a + bt 2, где a и b - постоянные векторы, причем a ^ b. Найти относительно точки O момент силы N, действующей на частицу, когда угол между векторами N и M окажется равным 450.
Ответ: N = 2 b 
5.3. Небольшой шарик массы m, привязанный на нити длины l к потолку в точке O, движется по горизонтальной окружности постоянной угловой скоростью w. Относительно каких точек момент импульса M шарика остается постоянным? Найти модуль приращения вектора момента импульса шарика относительно точки О за половину оборота.
Ответ: Относительно центра окружности. ½D M ½=2  mgl/w.
mgl/w.
5.4. На массивный неподвижный блок радиуса R намотана легкая нерастяжимая нить, к свободному концу которой подвешено небольшое тело массы m. В момент t = 0 систему предоставили самой себе, и она пришла в движение. Найти ее момент импульса относительно оси блока в зависимости от t.
Ответ: MZ = Rmgt.
5.5. Некоторая система частиц имеет суммарный импульс p и момент импульса M относительно точки O. Найти ее момент импульса M’ относительно точки O’, положение которой по отношению к точке O определяется радиус-вектором r0. Выяснить, в каком случае момент импульса системы частиц не будет зависеть от выбора точки O.
Ответ: M ’ = M - [ r 0 p ]. B случае, когда p = 0, т.е. в системе центра масс.
5.6. Небольшая шайба массы m = 50 г начинает скользить с вершины гладкой наклонной плоскости, высота которой h = 100 см и угол наклона к горизонту α = 150 . Найти модуль момента импульса шайбы относительно оси, перпендикулярной к плоскости рисунка, через t = 1,3 c после начала движения.
Ответ: M = mghtsin2α/2 = 1,6∙10-2 кг∙м2/с.
5.7. Найти момент импульса Земли относительно ее полярной оси. Считать Землю правильным шаром радиуса R = 6000 км, имеющим плотность r = 5,5 г/см3.
Ответ: M = 16rR5p2/15Т = 52∙1040 г∙см2/c.
5.8. Найти момент инерции: а) однородного тонкого стержня относительно оси, перпендикулярной к стержню и проходящей через его конец, если масса стержня m и его длина l; б) тонкой однородной прямоугольной пластинки относительно оси, проходящей через одну из вершин пластинки перпендикулярно к ее плоскости, если стороны пластинки равны a и b, а ее масса - m.
Ответ: а) I = ml2/3; б) I = m(a2 + b2)/3.
5.9. Найти момент инерции тонкого проволочного кольца радиусом а и массы m относительно оси, совпадающей с его диаметром.
Ответ: I = ma2/2.
5.10. Исходя из формулы для момента инерции однородного шара, найти момент инерции тонкого сферического слоя массы m и радиуса R относительно оси, проходящей через его центр.
Ответ: I = 2mR2/3.
5.11. На однородный сплошной цилиндр массы М и радиуса R плотно намотана легкая нить, к концу которой прикреплен груз массы m. В момент t = 0 система пришла в движение. Пренебрегая трением в оси цилиндра, найти зависимость от времени: а) модуля угловой скорости цилиндра; б) кинетической энергии всей системы.
Ответ: а) ω = gt/R(1+M/2m); б) Ek = mg2t2/2(1+M/2m).
5.12. Однородный шар массы m = 5,0 кг скатывается без скольжения по наклонной плоскости, составляющей угол α = 300 с горизонтом. Найти кинетическую энергию шара через t = 1,6 c после начала движения.
Ответ: Ek = 5mg2t2sin2α/14 = 0,11 кДж.

| 5.13. Найти ускорение грузов и натяжение нитей в установке, изображенной на рисунке 5.3, учитывая момент инерции I вращающегося блока, при условии, что нить не скользит по блоку. Радиус блока r.
Ответ: a2 = -a1 = (m2-m1)g/(m2+m1+I/r2);
T1 = (2m1m2g+m1gI/r2)/(m1+m2+I/r2);
T2 = (2m1m2g+m2gI/r2)/(m1+m2+I/r2).
|
| Рис.5.3
|
|
5.14. На горизонтальную неподвижную ось насажен блок, представляющий собой сплошной цилиндр массы М. Через него перекинута невесомая веревка, на концах которой висят две обезъяны массой m каждая. Первая обезъяна начинает подниматься с ускорением а относительно веревки. Определить, с каким ускорением относительно неподвижной системы координат будет двигаться вторая обезъяна.
Ответ: a2 = 2ma/(M+4m).
5.15. По наклонной плоскости, образующей угол α с горизонтом, скатывается без скольжения сплошной однородный диск. Найти линейное ускорение а центра диска.
Ответ: a = 2gsinα/3.
5.16. По наклонной плоскости, составляющей с горизонтом угол α=300, скатывается без скольжения сплошной однородный цилиндр, масса которого равна 300 г. Найти величину силы трения цилиндра о плоскость.
Ответ: F = mg sinα/3.
5.17. На краю свободно вращающегося горизонтального диска радиуса R, имеющего момент инерции I, стоит человек массы m. Диск совершает n об/мин. Как изменится скорость вращения диска, если человек перейдет от края диска к центру? Как изменится при этом кинетическая энергия? Размерами человека по сравнению с радиусом диска можно пренебречь.
Ответ: Скорость вращения и кинетическая энергия возрастут в (1+mR2/I) раз.
5.18. Найти ускорение а центра однородного шара, скатывающегося без скольжения по наклонной плоскости, образующей угол α с горизонтом. Чему равна сила трения сцепления шара и плоскости?
Ответ: a = 5g sinα/7; Tтр = 2mg sinα/7, где m – масса шара.
5.19. Однородный шар радиуса r скатывается без скольжения с вершины сферы радиуса R. Найти угловую скорость шара после отрыва от сферы. Начальная скорость шара пренебрежимо мала.
Ответ: 
5.20. Вертикально расположенный однородный стержень массы М и длины l может вращаться вокруг своего верхнего конца. В нижний конец стержня попала, застряв, летевшая пуля массы m, в результате чего стержень отклонился на угол α. Считая m«М, найти скорость летевшей пули.
Ответ: v = (M/m)(2gl/3)1/2sin(α/2).
К О Л Е Б А Н И Я
ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ
Колебания – это движения или процессы, которые характеризуются определенной повторяемостью во времени. Например, качание маятника, переменный электрический ток.
Колебания называются свободными, если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему. Важным среди колебательных движений является гармоническое колебательное движение. При таком движении колеблющаяся величина изменяется со временем по закону синуса (косинуса). Характер такого движения лучше рассматривать с помощью следующей кинематической модели. Пусть точка М равномерно вращается по окружности радиуса А с постоянной угловой скоростью w (рис.6.1).

Рис.6.1
Тогда ее проекция N на ось X, проходящую через диаметр, будет совершать колебательное движение от положения N1 до N2 и обратно. Это колебание точки N и будет гармоническим колебанием. Чтобы его описать, нужно найти координату x точки N как функцию времени t. Пусть в начальный момент времени t=0 радиус ОМ составлял с осью X угол d. Спустя время t этот угол получит приращение wt и станет равным α = wt+d. Тогда координата x точки N в данный момент t определится как
 .
.
Эта формула и описывает гармоническое колебание точки N.
Величина А дает максимальное отклонение колеблющейся точки от положения равновесия и называется амплитудой колебания. Величина w называется циклической частотой. Величину wt+d называют фазой колебания, а ее значение при t=0, т.е. значение d – начальной фазой колебания. Графически можно изобразить колебательное движение, если откладывать по горизонтальной оси время t, а по вертикальной оси – смещение x (рис.6.2). На рисунке амплитуда А = 2, начальная фаза d = 0.

Рис.6.2
Промежуток времени, через который фаза получит приращение 2π, а колеблющаяся точка вернется в исходное положение, называют периодом колебаний:
 .
.
Скорость колеблющейся точки:
 .
.
Ускорение:
 ,
,
или
 .
.
Последнее выражение есть дифференциальное уравнение гармонических колебаний.
Сила, действующая на материальную точку при гармоническом колебании, равна
 .
.
Она пропорциональна отклонению x и имеет противоположное ему направление, т.е. направлена к положению равновесия.
Кинетическая энергия материальной точки, совершающей гармонические колебания, равна
 .
.
Потенциальная энергия материальной точки, совершающей гармонические колебания под действием упругой силы F, равна
 .
.
Полная энергия:  .
.
Свободные затухающие колебания – колебания, амплитуда которых с течением времени уменьшается из-за потерь энергии колебательной системой (тепловые потери вследствие трения в механических колебаниях).
Дифференциальное уравнение свободных затухающих колебаний имеет вид
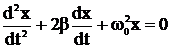 ,
,
где x –колеблющаяся величина, b - коэффициент затухания, w0 –циклическая частота свободных незатухающих колебания той же колебательной системы (т.е. при b=0).
Решение этого уравнения в случае малых затуханий (b << w0)
 ,
,
где  - амплитуда затухающих колебаний, а А0 – начальная амплитуда,
- амплитуда затухающих колебаний, а А0 – начальная амплитуда, 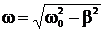 - частота затухающих колебаний (рис.6.3). Промежуток времени t=1/b, в течение которого амплитуда затухающих колебаний уменьшается в е – раз, называется временем релаксации.
- частота затухающих колебаний (рис.6.3). Промежуток времени t=1/b, в течение которого амплитуда затухающих колебаний уменьшается в е – раз, называется временем релаксации.

Рис.6.3
Под периодом затухающих колебаний понимают промежуток времени между двумя последующими максимумами (или минимумами) колеблющейся величины. Тогда
 .
.
Если А(t) и А(t+Т) – амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающихся на период, то величину


называют логарифмическим декрементом затухания.
Также для характеристики колебательной системы пользуются понятием добротности Q, которая при малых значениях логарифмического декремента равна
 .
.
Примеры решения задач
1.Вычислить период малых колебаний ареометра которому сообщили небольшой толчок в вертикальном направлении (рис.6.4). Масса ареометра m = 50 г, радиус его трубки r = 3,2 мм, плотность жидкости r = 1,00 г/см3. Сопротивление жидкости  считать пренебрежимо малым.
считать пренебрежимо малым.
 Дано:
Дано:
m = 50 г = 5·10-2 кг
r = 3,2 мм = 3,2·10-3 м
r = 1,00 г/см3 = 103 кг/м3
______________________
Т-?
Рис.6.4
Решение
В покое действующие на ареометр силы уравновешивают друг друга, поэтому в проекции на ось X:
mg - Fарх = 0.
Т.к. Fарх = Pж = rVжg = rπr2hg, то
mg = rπr2hg.
После толчка в вертикальном направлении:
ma =mg - Fарх
или
ma = mg - rπr2(h+x)g.
Отсюда, с учетом того, что 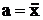 имеем
имеем
 .
.
Поскольку дифференциальное уравнение гармонических колебаний имеет вид
 ,
,
видим что в нашем случае
 .
.
Тогда
 .
.
Подставив численные значения, получим Т = 2,5 с.
2.Тело массой m = 100 г, совершая затухающие колебания, за время t = 1 мин потеряло 40 % своей энергии. Определить коэффициент сопротивления среды r.
Дано:
m = 100 г = 0,1 кг
t = 1 мин = 60 c
E(t+t) = 0,6E(t)
___________________
r-?
Решение
Сила трения при малых колебаниях  , где r- коэффициент сопротивления среды, v- скорость тела. Следовательно
, где r- коэффициент сопротивления среды, v- скорость тела. Следовательно  , где b - коэффициент затухания. Полная энергия колебаний
, где b - коэффициент затухания. Полная энергия колебаний
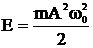 ,
,
 - амплитуда затухающих колебаний. Тогда
- амплитуда затухающих колебаний. Тогда
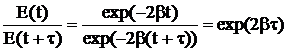 .
.
С другой стороны, по условию задачи
 .
.
Следовательно,
 .
.
Выражаем отсюда искомую величину:
 .
.
Подставив численные значения, имеем r = 8,5·10-4 кг/c.
СПИСОК ЗАДАЧ
6.1. Частица массы m находится в одномерном силовом поле, где ее потенциальная энергия зависит от координаты x как U(x) = U0(1-cos ax), U0 и а – постоянные. Найти период малых колебаний частицы около положения равновесия.
Ответ:  .
.
6.2. Частица массы m находится в одномерном силовом поле, где ее потенциальная энергия зависит от координаты x как U(x) = a/x2-b/x, где а и b – положительные постоянные. Найти период малых колебаний частицы около положения равновесия.
Ответ:  .
.
6.3. Неподвижное тело, подвешенное на пружине, увеличивает ее длину на Dl = 70 мм. Считая массу пружины пренебрежимо малой, найти период малых вертикальных колебаний тела.
Ответ: 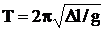 =0,52 с.
=0,52 с.
6.4. Определить период малых продольных колебаний тела массы m в системе, показанной на рис.6.5, если жесткости пружинок равны k1 и k2, а их массы и трение пренебрежимо малы. В положении равновесия пружинки не деформированы.
Ответ:  .
.


Рис.6.5 Рис.6.6
6.5. Найти период малых вертикальных колебаний тела массы m в системе, показанной на рис.6.6. Жесткости пружинок равны k1 и k2, а их массы пренебрежимо малы.
Ответ:  .
.
6.6. Найти зависимость от времени угла отклонения математического маятника длины l = 80 см, если в начальный момент маятник: а) отклонили на угол α = 3,00 и без толчка отпустили; б) находился в состоянии равновесия и его нижнему концу сообщили горизонтальную скорость v = 0,22 м/с.
Ответ: а)  б)
б)  .
.
6.7. Найти зависимость от времени угла отклонения математического маятника длины l = 80 см, если в начальный момент маятник отклонили на угол α = 3,00, а его нижнему концу сообщили скорость v = 0,22 м/с, направленную к положению равновесия.
Ответ:  .
.
6.8. Тело массы m упало с высоты h на чашку пружинных весов. Массы чашки и пружины пренебрежимо малы, жесткость пружины k. Прилипнув к чашке, тело начинает совершать гармонические колебания в вертикальном направлении. Найти амплитуду колебаний и их энергию.
Ответ:  ,
, 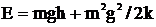 .
.
6.9. Уравнение колебания материальной точки массой m = 16 г имеет вид  м. Найти зависимость от времени силы F, действующей на точку и максимальное значение силы.
м. Найти зависимость от времени силы F, действующей на точку и максимальное значение силы.
Ответ: 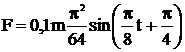 ; Fmax = 246 мкН.
; Fmax = 246 мкН.
6.10. К пружине подвешен груз. Максимальная кинетическая энергия колебаний груза Wmax = 1 Дж. Амплитуда колебаний А = 5 см. Найти жесткость пружины.
Ответ: k = 2Wmax/A2 = 800 Н/м.
6.11. Математический маятник совершает колебания в среде, для которой логарифмический декремент затухания d0 = 1,5. Каким будет значение d, если сопротивление среды увеличить в n = 2 раза? Во сколько раз следует увеличить сопротивление среды, чтобы колебания стали невозможны?
Ответ:  = 3,3;
= 3,3;  = 4,3.
= 4,3.
6.12. Найти добротность осциллятора, у которого: а) амплитуда смещения уменьшается в h = 2,0 раза через каждые n = 110 периодов колебаний; б) собственная частота w0 = 100 с-1 и время релаксации t = 60 с.
Ответ: а)  ; б)
; б)  = 3000.
= 3000.
6.13. К невесомой пружине подвесили грузик, и она растянулась на Dx = 9,8 см. С каким периодом будет колебаться грузик, если ему дать небольшой толчок в вертикальном направлении? Логарифмический декремент затухания d = 3,1.
Ответ:  =0,7 с.
=0,7 с.
6.14. Тело совершает крутильные колебания по закону  . Найти: а) угловую скорость и угловое ускорение тела в момент t = 0; б) моменты времени, когда угловая скорость максимальна.
. Найти: а) угловую скорость и угловое ускорение тела в момент t = 0; б) моменты времени, когда угловая скорость максимальна.
Ответ: а)  ; б)
; б)  , где n = 0,1,2,…
, где n = 0,1,2,…
6.15. На горизонтальной плоскости с коэффициентом трения m = 0,1 лежит брусок массы m = 0,5 кг, соединенный горизонтальной недеформированной пружинкой. Жесткость пружинки k = 2,45 Н/см, а ее масса пренебрежимо мала. Брусок сместили так, что пружинка растянулась на x0 = 3,0 см, и затем отпустили. Найти: а) период колебаний бруска; б) число колебаний, которое совершит брусок до остановки.
Ответ: а)  = 0,28 с; б)
= 0,28 с; б)  .
.
6.16. Период затухающих колебаний Т = 4 с, логарифмический декремент затухания d = 1,6, начальная фаза j = 0. При t = T/4 смещение точки x = 4,5 см. Написать уравнение движения этого колебания.
Ответ:  .
.
6.17. Найти логарифмический декремент затухания математического маятника, если за время t = 1 мин амплитуда колебаний уменьшилась в 2 раза. Длина маятника l = 1 м.
Ответ:  = 0,023.
= 0,023.
6.18. Математический маятник совершает затухающие колебания с логарифмическим декрементом затухания d = 0,2. Во сколько раз уменьшится полное ускорение маятника в его крайнем положении за одно колебание?
Ответ: n = a0/a = ed = 1,22.
6.19. Амплитуда затухающих колебаний математического маятника за время t1 = 1 мин уменьшилась вдвое. Во сколько раз уменьшится амплитуда за время t2 = 3 мин?
Ответ: 
6.20. К вертикально висящей пружинке подвешивают груз. При этом пружинка удлиняется на Dl = 9,8 см. Оттягивая этот груз вниз и отпуская его, заставляют груз совершать колебания. Каким должен быть коэффициент затухания b, чтобы логарифмический декремент затухания колебаний был равен d = 6?
Ответ:  = 6,89 с-1.
= 6,89 с-1.
Л И Т Е Р А Т У Р А
1. Иродов И.Е. Задачи по общей физике. М.: Наука, 1988.
2. Сборник задач по общему курсу физики. Механика. Под ред. Яковлева И.А. М.: Наука, 1977.
3. Сивухин Д.В. Общий курс физики. Т.1. Механика. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2002.



 ,
, .
. ,
, .
. ,
, ,
, .
. .
.
 -?
-? .
. Δ М = М 1- М, а затем его модуль. Момент импульса шайбы относительно точки О’ после удара о стенку(см.рисунок):
Δ М = М 1- М, а затем его модуль. Момент импульса шайбы относительно точки О’ после удара о стенку(см.рисунок): .
.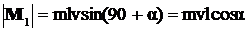 . Момент импульса шайбы относительно точки О до удара о стенку находится аналогично:
. Момент импульса шайбы относительно точки О до удара о стенку находится аналогично:  . Он также перпендикулярен плоскости, в которой движется шайба, но направлен от нас. По модулю
. Он также перпендикулярен плоскости, в которой движется шайба, но направлен от нас. По модулю  . Тогда приращение момента импульса Δ М = М 1- М= 2 М 1, а модуль приращения
. Тогда приращение момента импульса Δ М = М 1- М= 2 М 1, а модуль приращения  .
.
 ,
, - кинетическая энергия поступательного движения шарика,
- кинетическая энергия поступательного движения шарика,  - кинетическая энергия вращательного движения шарика.
- кинетическая энергия вращательного движения шарика.  - момент инерции шарика относительно оси, проходящей через его центр,
- момент инерции шарика относительно оси, проходящей через его центр,  - угловая скорость вращения. Подставив все в закон сохранения энергии, найдем скорость поступательного движения шарика:
- угловая скорость вращения. Подставив все в закон сохранения энергии, найдем скорость поступательного движения шарика: .
. .
. .
. .
.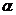 к горизонту с начальной скоростью v0. Найти модуль вектора момента импульса шарика относительно точки бросания в зависимости от времени движения. Вычислить M в вершине траектории, если m = 130 г,
к горизонту с начальной скоростью v0. Найти модуль вектора момента импульса шарика относительно точки бросания в зависимости от времени движения. Вычислить M в вершине траектории, если m = 130 г, 
 mgl/w.
mgl/w.


 .
.
 .
. .
. ,
, .
. .
. .
. .
. .
.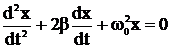 ,
, ,
, - амплитуда затухающих колебаний, а А0 – начальная амплитуда,
- амплитуда затухающих колебаний, а А0 – начальная амплитуда, 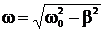 - частота затухающих колебаний (рис.6.3). Промежуток времени t=1/b, в течение которого амплитуда затухающих колебаний уменьшается в е – раз, называется временем релаксации.
- частота затухающих колебаний (рис.6.3). Промежуток времени t=1/b, в течение которого амплитуда затухающих колебаний уменьшается в е – раз, называется временем релаксации.
 .
.
 .
. считать пренебрежимо малым.
считать пренебрежимо малым. Дано:
Дано: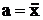 имеем
имеем .
. .
. .
. , где r- коэффициент сопротивления среды, v- скорость тела. Следовательно
, где r- коэффициент сопротивления среды, v- скорость тела. Следовательно  , где b - коэффициент затухания. Полная энергия колебаний
, где b - коэффициент затухания. Полная энергия колебаний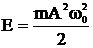 ,
,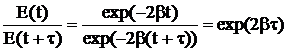 .
. .
. .
. .
. .
. .
.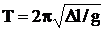 =0,52 с.
=0,52 с. .
.

 .
. б)
б)  .
. .
. ,
, 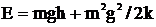 .
. м. Найти зависимость от времени силы F, действующей на точку и максимальное значение силы.
м. Найти зависимость от времени силы F, действующей на точку и максимальное значение силы.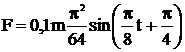 ; Fmax = 246 мкН.
; Fmax = 246 мкН. = 3,3;
= 3,3;  = 4,3.
= 4,3. ; б)
; б)  = 3000.
= 3000. =0,7 с.
=0,7 с. . Найти: а) угловую скорость и угловое ускорение тела в момент t = 0; б) моменты времени, когда угловая скорость максимальна.
. Найти: а) угловую скорость и угловое ускорение тела в момент t = 0; б) моменты времени, когда угловая скорость максимальна. ; б)
; б)  , где n = 0,1,2,…
, где n = 0,1,2,… = 0,28 с; б)
= 0,28 с; б)  .
. .
. = 0,023.
= 0,023.
 = 6,89 с-1.
= 6,89 с-1.


