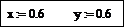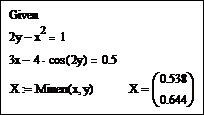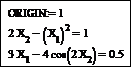Для вычисления суммы всех элементов вектора-столбца предназначен шаблон оператора суммирования 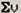 , кнопка которого находится на панели инструментов Matrix (Матрица). Достаточно задать вектор, отобразить шаблон оператора суммирования в документе Mathcad и вписать в поле ввода шаблона имя вектора:
, кнопка которого находится на панели инструментов Matrix (Матрица). Достаточно задать вектор, отобразить шаблон оператора суммирования в документе Mathcad и вписать в поле ввода шаблона имя вектора:
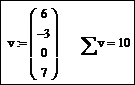
Суммирование и вычисление произведений элементов массива (вектора или матрицы) выполняется также с использованием соответствующих шаблонов показанной на рисунке 4 панели Calculus (Исчисление).
|
|

|
| Рисунок 4 – Панель инструментов Calculus
|
Например, после вставки в документ шаблона
.  .
.
необходимо задать четыре величины: переменную i, значениями которой являются номера элементов вектора, константу n, являющуюся номером (индексом) последнего учитываемого при суммировании элемента вектора, константу m, обозначающую номер первого учитываемого элемента вектора. Эти величины заносятся в поля ввода █ шаблона. Вычисление суммы производится нажатием клавиши =.. Результат представляется формульными областями
или формульной областью
.  .
.
Фрагмент документа Mathcad, в котором вычисляются сумма элементов второй строки и сумма всех элементов матрицы A имеет вид:
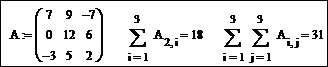
Фрагмент документа Mathcad, в котором вычисляется произведение элементов третьего столбца и произведение всех элементов матрицы A, включает следующие формульные области:
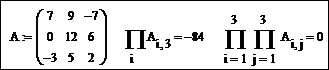
1.1.6 Решение задач обработки массивов в Mathcad
Пример 3. Ввести массив MS [1..5], состоящий из произвольных чисел, и значение var = 0,95. Для каждого элемента массива MS вычислить значение RES по формуле 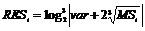 . Подсчитать сумму элементов массива RES. Найти минимальное значение RES. Отсортировать элементы массива RES по убыванию. Подсчитать произведение элементов массива RES, стоящих на нечетных местах. Найти косинус каждого элемента RES.
. Подсчитать сумму элементов массива RES. Найти минимальное значение RES. Отсортировать элементы массива RES по убыванию. Подсчитать произведение элементов массива RES, стоящих на нечетных местах. Найти косинус каждого элемента RES.
Решение.
Задайте порядок нумерации элементов в массивах, начиная с единицы, и ранжированную переменную для нумерации элементов создаваемых векторов MS и RES:
. 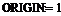 ..
.. 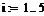 .
.
Введите имя исходного массива и знак присваивания. Не изменяя положение курсора-уголка, щелкните на кнопке с изображением матрицы дважды и в отобразившемся диалоговом окне укажите размерность вектора-столбца: Rows – количество строк 5, Columns – количество столбцов 1.
Введите произвольные значения элементов массива MS, используя для перехода от одного поля ввода к другому клавишу Tab или клавиши управления курсором:
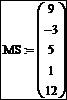
Присвойте значение переменной var:
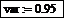
Наберите формулу для вычисления i -го элемента массива RES:
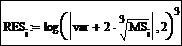
Для просмотра результатов в виде таблицы наберите MSi = и RESi =, а для вывода результатов в виде векторов-столбцов − MS = и RES =:

Вычислите сумму элементов массива RES. Для этого щелкните на кнопке  панели инструментов Matrix (Матрица), наберите в поле ввода █ имя массива RES и нажмите клавишу.=.. Формульная область примет вид:
панели инструментов Matrix (Матрица), наберите в поле ввода █ имя массива RES и нажмите клавишу.=.. Формульная область примет вид:
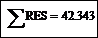
Для определения минимального элемента массива используйте функцию min. Ее применение по отношению к массиву RES приведет к результату
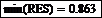
Выполните сортировку массива RES по возрастанию значений элементов, а затем измените порядок расположения элементов в массиве на обратный (от большего по величине значения к меньшему). Это достигается применением кода
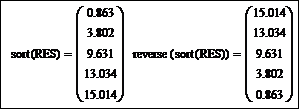
Вычислите произведение элементов, расположенных на нечетных местах, применив функцию if, как показано в формульной области
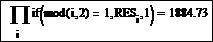
Примечание – Обращение к функции if имеет вид
if(< условие>, < выражение 1>, < выражение 2>)
где < условие> − логическое выражение, сформированное с использованием логических операций и операций отношения, набираемых посредством элементов панели инструментов Boolean (Логические);
< выражение 1> − выражение, которое выполнятся, если < условие> имеет значение «истина»;
< выражение 2> − выражение, которое выполнятся, если < условие> имеет значение «ложь».
В Mathcad допускается использование массива в качестве аргумента.
Вычисление, например, значения функции косинус каждого элемента массива RES осуществляется следующим образом:
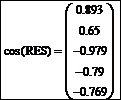
Пример 4. Задать матрицу M размером 10 × 10 согласно формуле
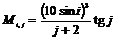 . (2)
. (2)
Создать подматрицу M 1 размером 5 × 5 из элементов M, расположенных на пересечении первых пяти строк и пяти последних столбцов.
Найти сумму элементов M 1.
Подсчитать произведение тех элементов матрицы M 1, сумма значений индексов которых является четным числом.
Определить минимальный элемент второй строки M 1.
Создать матрицу M 2, каждый элемент которой – десятичный логарифм соответствующего элемента матрицы M 1.
Комплексные элементы матрицы M 2 заменить их действительной частью.
Найти максимальные элементы в нечетных столбцах M 2.
Определить количество отрицательных элементов массива M 2.
Сформировать вектор z из диагональных элементов матрицы M 2 и найти его модуль.
Сформировать вектор w из элементов третьего столбца M 2.
Создать матрицу M 3 из четных строк матрицы M 2 и векторов z и w.
Решение.
Определите переменную ORIGIN и ранжированные переменные для нумерации элементов массивов (каждая формула в отдельном блоке):
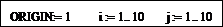
Создайте матрицу M и ее подматрицу M 1, используя встроенные функции:
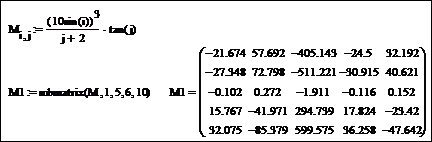
Вычислите сумму элементов M 1, вызывая дважды шаблон суммирования панели Calculus (Исчисление):
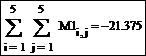
Вычислите произведение тех элементов матрицы M 1, у которых сумма значений индекса i и индекса j является четным числом. Для этого с помощью функции if при нахождении произведения замените элементы, не удовлетворяющие данному условию, на единицу. Соответствующая формульная область имеет вид:
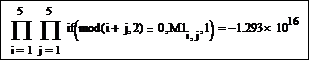
Найдите минимальный элемент второй строки M 1, выполнив транспонирование матрицы, а затем применив функцию min по отношению ко второму столбцу транспонированной матрицы:
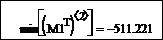
Создайте матрицу M 2 посредством операции векторизация, набрав выражение log(M1) и щелкнув мышью на кнопке  панели инструментов Matrix (Матрица):
панели инструментов Matrix (Матрица):

Выделите действительные части элементов комплексной матрицы:

Найдите максимальные элементы в каждом нечетном столбце матрицы M 2, задав последовательность из нечетных индексов матрицы посредством ранжированной переменной k, выделив (сформировав) необходимые векторы-столбцы M2<k> и применив функцию max, возвращающую максимальный элемент каждого нечетного столбца матрицы. Фрагмент документа Mathcad, выполняющий эти действия, имеет вид:
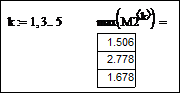
Определите количество отрицательных элементов матрицы M 2, воспользовавшись функцией
if(M2i,j < 0, 1, 0),
которая возвращает значение 1 для отрицательного элемента матрицы и 0 для положительного элемента матрицы. Сумма всех единиц в этом случае совпадает с количеством отрицательных элементов матрицы M 2:
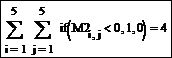
Создайте вектор z из элементов матрицы M 2 и вычислите его модуль. Сформируйте вектор на основе третьего столбца матрицы M 2. Данные действия реализует следующий фрагмент документа Mathcad:
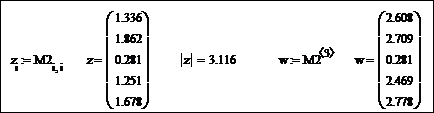
Создайте матрицу M 3 из четных строк матрицы M 2 и векторов z и w. Для этого транспонируйте матрицу M 2, сформируйте из нее необходимые вектор-столбцы и используйте функцию augment, чтобы объединить массивы с одинаковым количеством строк. Соответствующий фрагмент документа Mathcad имеет вид:
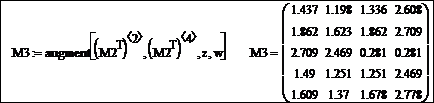
1.2 Решение уравнений и систем уравнений средствами Mathcad
Пакет Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений.
1.2.1 Функция root, блоки Given…Find и Given…Minerr
В ходе нахождения корней уравнения обычно выделяют два этапа:
1) отделение корней − определение интервала нахождения каждого корня или определение приблизительного значения корня. В Mathcad наиболее наглядным является отделение корней уравнения графическим способом;
2) уточнение корней − нахождение численного значения корня с заданной точностью.
Точность нахождения корня устанавливается с помощью системной переменной TOL (Convergence Tolerance − Допустимое отклонение), значение которой по умолчанию равно 10-3. Чем меньше значение TOL, тем с большей точностью, вообще говоря, находится корень уравнения.
Чтобы переопределить значение системной переменной TOL, необходимо посредством команды Math / Options открыть диалоговое окно математических свойств документа Options, перейти на вкладку Build-In Variables (Встроенные переменные) и в поле TOL (Convergence Tolerance) ввести новое значение, например, 0.0001. Это значение распространяется на весь документ Mathcad. Присваивание системной переменной TOL непосредственно в документе Mathcad нового значения, например,
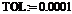 , (3)
, (3)
изменяет TOL для всех формульных и графических областей, расположенных правее и ниже оператора присваивания (3).
Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, формат обращения к которой имеет вид:
root(f(x), x, [ a, b ]).
Данная функция возвращает значение переменной x, при котором функция f (x) обращается в ноль. Аргументы функции root:
f (x) – функция в левой части уравнения f (x) = 0;
x – переменная, относительно которой требуется решить уравнение;
a, b – необязательные действительные числа, такие что a < b, причем на интервале [ a, b ] находится только один корень.
Если функция root не может найти корни уравнения, то рекомендуется уточнить начальное приближение, изменить границы интервала [ a, b ] нахождения корня или увеличить значение системной переменной TOL.
Для решения уравнений или систем нескольких уравнений и неравенств используются функции Find или Minerr, каждая из которых завершает формирование в документе Mathcad вычислительного блока, начинающегося ключевым словом Given и включающего в себя набор уравнений и неравенств.
Функция
Find(x 1, x 2, …, x n)
возвращает значения n неизвестных x 1, x 2, … x n, обращающих уравнения в тождества, т. е. возвращает решение системы уравнений. В случае решения системы из n уравнений с n неизвестными эта функция возвращает вектор, состоящий из n элементов.
Функция Find позволяет находить и решение одного уравнения с одной неизвестной, хотя для этой цели обычно используется функция root.
Если в результате поиска не может быть получено решение с заданной точностью, то функция Find выдает сообщение об ошибке. В этом случае можно использовать функцию
Minerr(x 1, x 2, …, x n),
возвращающую решение системы уравнений или одного уравнения (число уравнений должно быть равно числу неизвестных).
Порядок применения вычислительных блоков Given..Find и Given..Minerr для численного решения уравнений и систем уравнений:
· всем неизвестным, входящим в систему, присваивается начальное приближение;
· при необходимости задаются требуемые значения системным переменным TOL и CTOL (Constraint Tolerance − Допустимое отклонение ограничений);
· вводится ключевое слово Given, начинающее вычислительный блок;
· набираются уравнения и ограничения в виде неравенств (если необходимо) в произвольном порядке, каждое в отдельной формульной области, причем для записи используются операции отношения панели Boolean (Логические). Допускается использование двусторонних неравенств вида a ≤ x ≤ b;
· применяется функция Find или Minerr.
Внутри блока решения недопустимы следующие операции и выражения:
· ранжированные переменные;
· выражения, содержащие знак ≠;
· локальное (:=) или глобальное (≡) определение переменных и функций, за исключением выражения, в с которое входит функция Find или Minerr;
· вложенный вычислительный блок.
В случае появления сообщения об ошибке вида
 ,
,
означающей, что решение не было найдено, рекомендуется изменить начальное приближение или значения системных переменных TOL и CTOL.
Пример 5. Решить уравнение
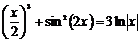 . (4)
. (4)
Решение.
Приведите уравнение к стандартной форме 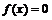 , перенося все слагаемые в его левую часть:
, перенося все слагаемые в его левую часть:
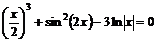 (5)
(5)
Определите функцию пользователя
Вставьте в документ шаблон двумерного графика в декартовой системе координат. Для этого щелкните на пиктограмме с изображением графика  сначала на панели Math (Математика), затем на панели Graph (График) или выполните команду Insert / Graph / X-Y Plot (Вставка / График / X-Y график). В документе Mathcad отобразится шаблон двумерного графика
сначала на панели Math (Математика), затем на панели Graph (График) или выполните команду Insert / Graph / X-Y Plot (Вставка / График / X-Y график). В документе Mathcad отобразится шаблон двумерного графика
В поле ввода █ в центре под осью абсцисс наберите имя аргумента x, а слева от оси ординат – имя функции с аргументом f (x):
Щелкните левой кнопкой мыши вне шаблона. В документе Mathcad отобразится графическая область
.  .
.
По умолчанию Mathcad при построении графика использует стандартный диапазон изменения x от –10 до 10.
Уменьшите значения левой и правой границы x, заменив число –10 на –5, а число 10 на 5 соответственно. Введите максимальное значение функции 15, а минимальное − 10.
Отформатируйте график функции f(x). Для этого щелкните правой кнопкой мыши на графической области и выполните команду Format (Формат) контекстного меню. В окне приложения Mathcad отобразится диалоговое окно, показанное на рисунке 5.
Добавьте координатную сетку, установив флажки слева от строк Grid Lines ( Вспомогательные линии) для оси X и оси Y.
Отмените режим Autogrid и установите значения 10 и 5 в полях Number of grids (Количество линий) по оси Х и Y соответственно.
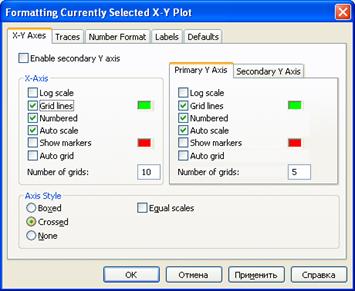
Рисунок 5 – Установка параметров форматирования декартова графика
Подтвердите внесенные изменения, щелкнув последовательно на кнопках Apply (Применить) и ОК.
Графическая область примет вид:
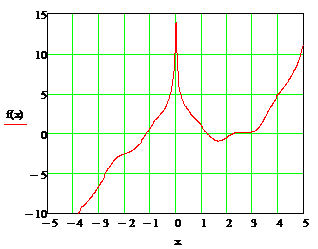
Назначьте стиль осей графика Crossed (Пересечение, Только оси).
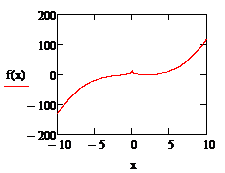
После указанных преобразований график функции f (x) примет вид:
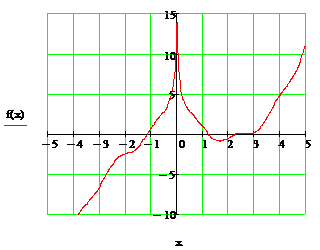
Из графика функции f (x) видно, что уравнение
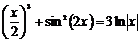 (6)
(6)
имеет три корня, которые приблизительно равны: x1» –1; x2» 1; x3» 2,5.
Этап отделения корней завершен.
Уточните теперь корни уравнения различными способами.
1Присвойте начальное приближение переменной x и укажите точность поиска корня:
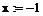
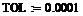 о
о
Уточните заданное приближение к значению корня с помощью функции root:
Выполните проверку, подтверждающую, что первый корень найден с заявленной точностью:
. 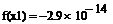 .
.
Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня. Уточнение второго корня произведите следующим образом:
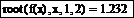
2 Присвойте начальное приближение переменой x для уточнения третьего корня:
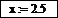
Наберите служебное слово Given, а затем уравнение f (x) = 0, разделяя его левую и правую части знаком логического равенства (полужирное равно =), который вставляется нажатием комбинация клавиш Ctrl =, или щелчком мыши на кнопке  панели Boolean (Логические). Завершите вычислительный блок оператором присваивания x 3:= Find(x) и выведите значение найденного третьего корня.
панели Boolean (Логические). Завершите вычислительный блок оператором присваивания x 3:= Find(x) и выведите значение найденного третьего корня.
Фрагмент документа Mathcad, в котором уточняется корень уравнения с помощью вычислительного блока Given…Find, имеет вид:
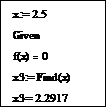
3 Применение вычислительного блока Given…Minerr для нахождения первого корня осуществляется следующим образом:
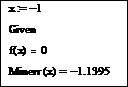
Примечание − Для уточнения корня в данном примере установлена точность 0,0001. Поэтому целесообразно изменить формат вывода результатов (4 знака после десятичного разделителя) в диалоговом окне форматирования результатов на вкладке Number Format.
Пример 6. Решить систему уравнений
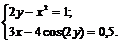 (7)
(7)
Решение.
Отделите решения системы графически. Определите две функции аргументов х и y соответственно, выразив для этого из первого уравнения системы у, а из второго – х:
о 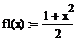
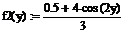 о
о
Для более детального построения графика создайте ранжированные переменные:
о 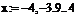
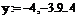 о
о
Вставьте в документ Mathcad шаблон графика X-Y Plot. Аргументы по оси абсцисс и ординат введите через запятую. После форматирования график примет вид:
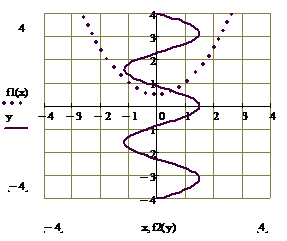
Значения координат точки, в которой пересекаются линии графиков функций, являются решением системы уравнений. Присвойте приблизительные значения координат точки пересечения в качестве начального приближения для переменных x и y:
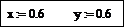
Наберите ключевое слово Given, а затем уравнения системы, каждое в отдельной формульной области, отделяя левую и правую части знаком логического равенства = (Ctrl =). Решение уточните с помощью функции Minerr:
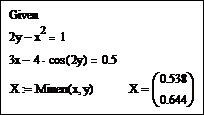
Выполните проверку найденного решения системы уравнений. Для этого задайте значение системной переменной ORIGIN:=1. Первый элемент вектора X − это значение переменной x, а второй − значение переменной y. Подставьте их в левые части уравнений системы и произведите вычисления:
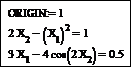
Сравните полученные значения 1 и 0,5 со значениями правых частей уравнений (7). Видно, что они совпадают. Следовательно, система уравнений решена правильно.





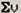 , кнопка которого находится на панели инструментов Matrix (Матрица). Достаточно задать вектор, отобразить шаблон оператора суммирования в документе Mathcad и вписать в поле ввода шаблона имя вектора:
, кнопка которого находится на панели инструментов Matrix (Матрица). Достаточно задать вектор, отобразить шаблон оператора суммирования в документе Mathcad и вписать в поле ввода шаблона имя вектора: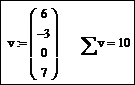

 .
.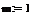 .
.
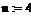 .
.
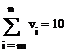 .
.
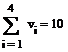 .
.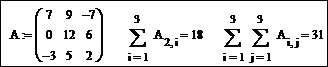
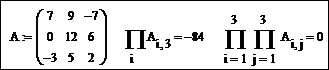
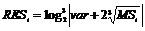 . Подсчитать сумму элементов массива RES. Найти минимальное значение RES. Отсортировать элементы массива RES по убыванию. Подсчитать произведение элементов массива RES, стоящих на нечетных местах. Найти косинус каждого элемента RES.
. Подсчитать сумму элементов массива RES. Найти минимальное значение RES. Отсортировать элементы массива RES по убыванию. Подсчитать произведение элементов массива RES, стоящих на нечетных местах. Найти косинус каждого элемента RES.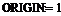 ..
.. 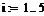 .
.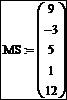
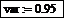
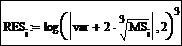

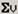 панели инструментов Matrix (Матрица), наберите в поле ввода █ имя массива RES и нажмите клавишу.=.. Формульная область примет вид:
панели инструментов Matrix (Матрица), наберите в поле ввода █ имя массива RES и нажмите клавишу.=.. Формульная область примет вид: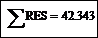
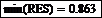
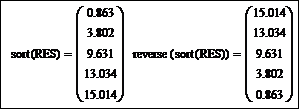
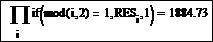
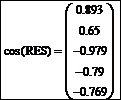
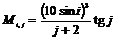 . (2)
. (2)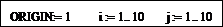
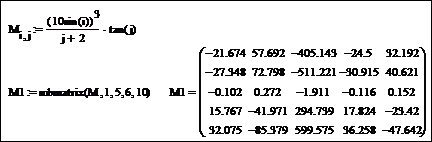
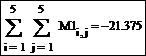
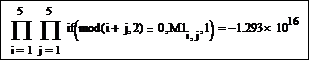
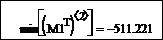
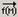 панели инструментов Matrix (Матрица):
панели инструментов Matrix (Матрица):

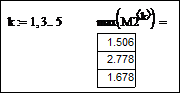
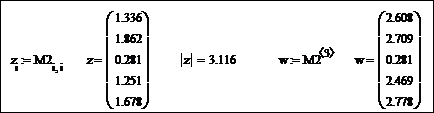
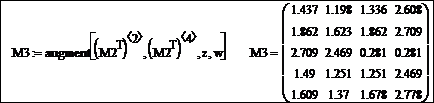
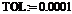 , (3)
, (3) ,
,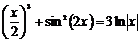 . (4)
. (4)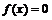 , перенося все слагаемые в его левую часть:
, перенося все слагаемые в его левую часть: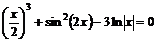 (5)
(5)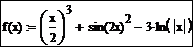
 сначала на панели Math (Математика), затем на панели Graph (График) или выполните команду Insert / Graph / X-Y Plot (Вставка / График / X-Y график). В документе Mathcad отобразится шаблон двумерного графика
сначала на панели Math (Математика), затем на панели Graph (График) или выполните команду Insert / Graph / X-Y Plot (Вставка / График / X-Y график). В документе Mathcad отобразится шаблон двумерного графика

 .
.


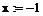
 о
о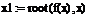
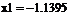
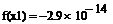 .
.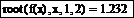
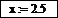
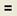 панели Boolean (Логические). Завершите вычислительный блок оператором присваивания x 3:= Find(x) и выведите значение найденного третьего корня.
панели Boolean (Логические). Завершите вычислительный блок оператором присваивания x 3:= Find(x) и выведите значение найденного третьего корня.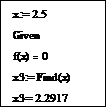
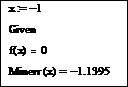
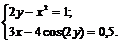 (7)
(7)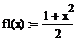
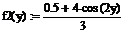 о
о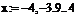
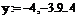 о
о