

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...
Топ:
Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы...
Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда...
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Интересное:
Как мы говорим и как мы слушаем: общение можно сравнить с огромным зонтиком, под которым скрыто все...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Для устранения ступенчатого эффекта в растровых изображениях используют методы выравнивания и сглаживания. Основная идея этого метода состоит в том, что видимые линии и отрезки имеют ненулевую толщину. И для их отображения на экране или бумаге используются пиксели, которые также имеют ненулевую площадь.
Чтобы растровое изображение выглядело более гладким, цвет угловых пикселей «ступенек» заменяется на некоторый оттенок, промежуточный между цветом объекта и цветом фона:
Cx = (CSx + Cф(S – Sx)) / S,
где Cx – искомый оттенок цвета углового пикселя; S – площадь пикселя; Sx – часть площади пикселя, перекрываемая идеальным контуром векторного объекта; Cф – цвет фона; C – цвет объекта.
Таким образом, устранение ступенчатого эффекта достигается за счет размывания контура объекта (рис. 3.2).
 |
Рис. 3.2. Устранение ступенчатого эффекта.
3.3. Заполнение области (закрашивание)
Область представляет собой группу примыкающих друг к другу связанных пикселей.
Области пикселей могут задаваться различными способами [17].
Внутренне-определенные области задаются своими внутренними значениями: все пиксели в области имеют одно значение цвета и ни один из пикселей, принадлежащих границе области, не принимает этого значения.
Гранично-определенные области – все пиксели, принадлежащие границе, имеют одинаковое значение цвета и ни один из пикселей области не принимает этого значения.
Заполнение области – это присваивание всем пикселям, лежащим внутри области, некоторого общего значения цвета.
Рассмотрим простейший алгоритм закрашивания гранично-определенной области. На первом этапе находится пиксель, лежащий внутри области. Ему присваивается значение цвета заполнения. Затем проводится анализ цветов всех соседних пикселей. Если цвет соседнего пикселя не равен цвету границе или цвету заполнения, то цвет этого пикселя изменяется на цвет заполнения. Потом анализируется цвет пикселей, соседних с уже рассмотренными, и для них повторяется процедура закраски.
|
|
Восьмисвязные алгоритмы закраски могут давать выход за пределы области (рис. 3.3).
 |
Рис. 3.3. Выход за границу области при 8-связном алгоритме закрашивания.
Как видно из рисунка, для правильного выполнения алгоритма закрашивания граница 8-связной области должна быть 4-связна.
Большую скорость закрашивания обеспечивают алгоритмы, которые обрабатывают не отдельные пиксели, а сразу блоки пикселей (отрезки, прямоугольники).
Закрашивание области линиями заключается в том, что на каждом шаге закрашивания рисуется горизонтальный отрезок максимальной длины, который размещается между пикселями границы. Затем проверяются пиксели, лежащие непосредственно над и под отрезком. Если находятся незаполненные пиксели, то отрисовывается новый отрезок.
3.4. Алгоритмы закрашивания, использующие математическое описание контура
Данные алгоритмы закрашивания не требуют обязательного предварительного создания пикселей границы области. Математическим описанием контура фигуры может служить уравнение кривой (окружности, эллипса). Для многоугольников контур задается множеством координат вершин (хi, уi) и соединяющих их отрезков.
Наиболее просто заполнить прямоугольник со сторонами, параллельными осям координат, заданный координатами диагональных углов (х1, у1) и (х2, у2), причем x1<x2, y1<y2:
for (y=y1; y<=y2; y=y+1)
{ // Рисуется горизонтальная линия
line (x1, y, x2, y); // от точки с координатами (x1, y)
} // до точки (x2, y).
Рассмотрим более подробно алгоритм заполнения многоугольника произвольной формы [10].
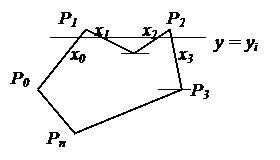 Пусть задан многоугольник с вершинами Р0, Р1, …, Рn (рис. 3.4). Наиболее популярный алгоритм закрашивает многоугольник отрезками прямых горизонтальных линий. Для каждой из горизонталей у = уi. находятся ординаты точек пересечения со всеми отрезками контура многоугольника. Затем проводится сортировка по возрастанию значений массива хj. Многоугольник закрашивается путем рисования отрезков (х0, уi; х1, уi), (х2, уi; х3, уi), (х4, уi; х5, уi) и так далее.
Пусть задан многоугольник с вершинами Р0, Р1, …, Рn (рис. 3.4). Наиболее популярный алгоритм закрашивает многоугольник отрезками прямых горизонтальных линий. Для каждой из горизонталей у = уi. находятся ординаты точек пересечения со всеми отрезками контура многоугольника. Затем проводится сортировка по возрастанию значений массива хj. Многоугольник закрашивается путем рисования отрезков (х0, уi; х1, уi), (х2, уi; х3, уi), (х4, уi; х5, уi) и так далее.
|
|
Рис. 3.4. Закрашивание многоугольника.
Для правильного заполнения многоугольника рассмотренным способом количество точек пересечения отрезков контура с каждой из горизонталей у = уi должно всегда быть четным. Если горизонталь проходит через вершину многоугольника, то должен проводиться дополнительный анализ:
· если горизонталь при прохождении через вершину пересекает контур многоугольника (на рис. 3.4 это вершины Р0 и Р4), то в массив хj записывается только одна координата точки пересечения;
· если горизонталь касается вершины (вершины Р1, Р2, Р3 и Рn), не пересекая в этой точке контур, то координаты точки касания в массив хj или не записываются, или записываются дважды.
4. АЛГОРИТМЫ ОТСЕЧЕНИЯ
Очень часто координаты некоторых точек рисуемых объектов, хранимые в прикладной базе данных, могут выходить за границы видимости (окна устройства вывода). То есть, объекты сначала должны пройти процесс отсечения и перевода координат составляющих их точек в координаты устройства вывода, лишь затем они могут быть визуализированы. Область отсечения, как правило, представляет из себя прямоугольник.
В простейшем случае – при отсечении двумерного отрезка относительно прямоугольного окна необходимо произвести вычисление координат точек пересечения отрезка с границами окна. Для сокращения объема вычислений и уменьшения числа операций умножения и деления используются различные алгоритмы, одним их которых является алгоритм Коэна-Сазерленда [20]. В этом алгоритме картинная плоскость разбивается на девять областей прямыми, проходящими через стороны отсекающего прямоугольника. Каждой из областей присваивается 4-битовый код, где установленный нулевой бит означает, что область лежит выше прямоугольника, первый бит – что область лежит ниже прямоугольника, второй бит – что область лежит правее прямоугольника, а третий бит – что область лежит левее прямоугольника (рис. 4.1).
|
|

Рис. 4.1. Коды областей картинной плоскости.
Путем анализа кодов областей, в которые попадают начальная и конечная точки каждого отрезка, выявляются отрезки, для которых необходимо проводить отсечение, и отбрасываются отрезки, которые лежат за границами отсекающей области. Вычисление точек пересечения выполняется только там, где это действительно необходимо. Для анализа кодов достаточно только булевых побитовых операций над двоичными числами.

Рис. 4.2. Последовательное применение алгоритма Сазерленда-Ходгмана для отсечения многоугольника относительно видимого окна.
На вход алгоритма поступает последовательность вершин исходного многоугольника. Алгоритм последовательно «обходит» по периметру весь многоугольник, проверяя на каждом шаге соотношение между последовательными вершинами и отсекающей границей. В выходной список вершин последовательно заносятся координаты вершин многоугольника, лежащие внутри отсекающей границы, и координаты точек пересечения ребер многоугольника с границей. То есть, если ребро полностью лежит внутри границы, то в выходной список заносятся обе вершины; если ребро сечется границей, то в выходной список заносятся вершина, лежащая внутри отсекаемой области, и точка пересечения ребра с отсекающей границей.
5. АФФИНЫЕ ПРЕОБРАЗОВАНИЯ
Геометрические преобразования широко применяются в компьютерной графике при выводе изображения на экран и проведении с ним разнообразных действий [2, 10, 14, 16, 17].
Перед тем, как приступить к рассмотрению различных случаев аффинных преобразований, определим используемые системы координат.
Аффинные преобразования рассматриваются в прямоугольных декартовых системах координат. На плоскости используется правосторонняя система координат – ось х (ось абсцисс) направлена направо, ось у – вверх, за положительное направление поворота принято направление против часовой стрелки. Трехмерная система координат правосторонняя – ось z (ось аппликат) направлена на наблюдателя; положительное направление поворота – против часовой стрелки, если смотреть из конца положительной полуоси в начало координат.
|
|
5.1. Аффинные преобразования на плоскости
Пусть на плоскости в прямоугольной системе координат задана точка N (х, у), которая в результате последовательных преобразований переводится в точку N * с координатами (х *, у *). В случае аффинных преобразований координаты конечной точки можно описать уравнениями вида:
x* = axx + bxy + cx,
y* = ayx + byy + cy,
где ax, bx, cx, aу, bу и cу – некоторые коэффициенты.
В аффинных преобразованиях на плоскости особую роль играют несколько важных частных случаев (поворот, масштабирование, отражение и перенос), имеющих хорошо прослеживаемые геометрические характеристики [7].
 Поворот вокруг начала координат на угол j описывается следующими уравнениями (рис. 5.1):
Поворот вокруг начала координат на угол j описывается следующими уравнениями (рис. 5.1):
x* = x cosj - y sinj,
y* = x sinj + y cosj.
Рис. 5.1. Поворот вокруг начала координат
Растяжение-сжатие (масштабирование) вдоль координатных осей и относительно начала координат:
x* = Mx x,
y* = My y.
Mx > 0, My > 0.
Растяжение вдоль оси абсцисс (ординат) имеет место при Mx > 1 (My > 1), сжатие – при Mx < 1 (My < 1).
 Отражение относительно координатных осей (рис. 5.2) описывается следующими уравнениями:
Отражение относительно координатных осей (рис. 5.2) описывается следующими уравнениями:
· относительно оси абсцисс
x* = x, y* = -y;
· относительно оси ординат
x* = -x, y* = y.
Рис. 5.2. Отражение относительно оси абсцисс
Перенос точки вдоль оси абсцисс на величину Dx, и на величину Dy вдоль оси ординат:
x* = x + Dx,
y* = y + Dy.
В компьютерной графике чаще используется матричная запись этих формул. Матрицы, соответствующие случаям поворота, масштабирования и отражения, строятся легко, но для записи уравнений переноса в матричной форме приходится использовать однородные координаты.
Пусть N – произвольная точка плоскости с координатами x и y. Однородными координатами этой точки называется любая тройка одновременно не равных нулю чисел x1, x2, x3, связанных с заданными числами x и y следующими соотношениями:
x = x1 / x3, y = x2 / x3, x3 ¹ 0.
В проективной геометрии для однородных координат принято следующее обозначение:
x: y: 1 (третья координата равна единице, поэтому операции деления не требуется; более общая форма записи x1: x2: x3).
При помощи троек однородных координат и матриц третьего порядка можно описать любое аффинное преобразование на плоскости уравнениями вида:
 = [ P ]
= [ P ] 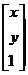 ,
,
где  и
и 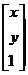 – векторы-столбцы координат конечной и начальной точек соответственно, [ P ] – матрица соответствующего преобразования, имеющая для двумерного случая размер 3X3.
– векторы-столбцы координат конечной и начальной точек соответственно, [ P ] – матрица соответствующего преобразования, имеющая для двумерного случая размер 3X3.
|
|
Поворот:
 =
= 
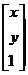 ,
,
Масштабирование:
 =
= 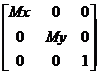
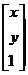 , Mx > 0, My > 0.
, Mx > 0, My > 0.
Отражение:
относительно оси абсцисс относительно оси ординат
 =
= 
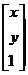 .
.  =
= 
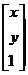 .
.
Перенос:
 =
= 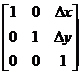
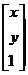 .
.
5.2. Аффинные преобразования в пространстве
Общее уравнение трехмерного аффинного преобразования:
x* = axx + bxy + cxz + dx,
y* = ayx + byy + cyz + dy,
z* = azx + bzy + czz + dz,
где ax, bx, cx, dx, aу, bу, cу, dy, az, bz, cz и dz – некоторые коэффициенты.
В пространственных преобразованиях выделяются те же основные частные случаи, что и в двумерных преобразованиях.
Повороты.
· Поворот вокруг оси абсцисс (оси х) на угол j:
x* = x,
y* = y cosj - z sinj,
z* = z cosj + y sinj.
В матричной форме с использованием однородных координат:
 .
.
· Поворот вокруг оси ординат (оси у) на угол j:
x* = x cosj + z sinj,
y* = y,
z* = z cosj - x sinj.
В матричной форме:  .
.
· Поворот вокруг оси аппликат (оси z) на угол j:
x* = x cosj - y sinjx,
y* = y cosj + x sinj,
z* = z.
Или, в матричной форме: 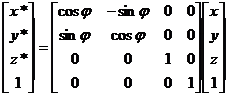 .
.
В случае поворотов в отрицательных направлениях значения углов берутся со знаком минус и используются тождества:
cos(-a) = cosa, sin(-a) = -sina.
Трехмерный перенос является простым расширением двумерного случая:
 или
или  .
.
Иногда необходимо выполнить перенос на величину, не являющуюся константой, а зависящую от начальных координат точки [11]. Это преобразование описывается следующими формулами:
 или
или  .
.
Масштабирование описывается следующими уравнениями:
x* = Mxx,
y* = Myy, Mx>0, My>0, Mz>0.
z* = Mzz.
Или:  .
.
В отличие от двумерного случая, в пространстве рассматриваются случаи отражения относительно координатных плоскостей.
· Отражение относительно плоскости z = 0:
 или
или  .
.
· Отражение относительно плоскости у = 0:
 или
или  .
.
· Отражение относительно плоскости х = 0:
 или
или  .
.
5.3. Композиция преобразований
Любое аффинное преобразование на плоскости или в пространстве можно представить как последовательное исполнение рассмотренных выше частных случаев. При таком подходе итоговую матрицу преобразования вычисляют как произведение матриц частных случаев, из которых складывается итоговое преобразование.
Следует помнить, что перемножение матриц является некоммутативной операцией, т.е. важен порядок ее выполнения.
Правильный порядок перемножения определяется положением матрицы частного преобразования относительно матрицы координатного вектора. Матрица, ближайшая к матрице координатного вектора, задает первое частное преобразование; а наиболее удаленная от него матрица задает последнее частное преобразование.
Пусть точка М с координатами (х, у, z) последовательно подвергается преобразованиям вида P 1, P 2, …, P n. Причем, [ P 1] – матрица первого преобразования (размером 4х4), а [ Pn ] – последнего. Итоговые координаты точки (х*, у*, z*) могут быть вычислены по уравнению:
 = [ Pn ] …[ P 2] [ P 1]
= [ Pn ] …[ P 2] [ P 1]  ,
,
или, в другой форме записи:
(x* y* z* 1) = (x y z 1) [ P 1] Т [ P 2] Т … [ Pn ] Т,
где [ Pi ] Т – транспонированная матрица [ Pi ].
Во второй форме записи координаты точек записываются как векторы-строки, а не вектора-столбцы.
ПРОЕЦИРОВАНИЕ
В настоящее время абсолютное большинство устройств вывода графической информации создают изображения на плоскости – экране монитора, бумаге и т.п. Несоответствие между объемными объектами и плоскими изображениями устраняется путем введения проекций, которые отображают трехмерные объекты на двумерной картинной плоскости.
Проекция объекта на картинную плоскость строится при помощи проецирующих лучей, которые выходят из одной точки (центра проекции) и проходят через каждую точку объекта. Пересечение этих лучей с картинной плоскостью и образует проекцию.
В зависимости от удаленности центра проекции и взаимного расположения картинной плоскости, проецирующих лучей и осей координат выделяется несколько видов проекций (рис. 6.1) [10, 14, 16, 17].
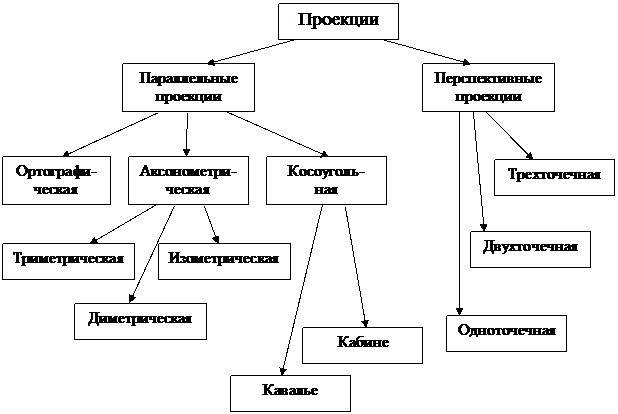
Рис. 6.1. Виды проекций.
При параллельном проецировании центр проекции считается лежащим в бесконечности (проецирующие лучи параллельны друг другу), а при перспективном (центральном) проецировании расстояние между центром проекции и картинной плоскостью конечно.
Виды параллельных проекций
В ортографических и аксонометрических проекциях проецирующие лучи перпендикулярны картинной плоскости (направление проецирования совпадает с нормалью к проекционной плоскости).
Во всех параллельных проекциях грани отображаемого объекта, параллельные картинной плоскости, изображаются без искажения формы и размеров; параллельные в пространстве прямые сохраняют параллельность и после проецирования, а также остаются постоянными относительные длины параллельных в исходном пространстве линий.
Самой простой из параллельных проекций является ортографическая проекция, при которой картинная плоскость совпадает с одной из координатных плоскостей или параллельна ей (рис. 6.2), а проецирующие лучи параллельны одной из координатных осей.
 |
Рис. 6.2. Ортографическая проекция на плоскость z = 0.
Матрица проецирования на координатную плоскость z = 0 имеет вид:
[ P орт z ] =  ,
,
а при проецировании на параллельную ей плоскость z = r:
[ P орт z ] =  .
.
Аналогично, матрицы проецирования на плоскости x = p и y = q равны:
[ P орт x ] =  , [ P орт y ] =
, [ P орт y ] =  .
.
Наиболее часто используются наборы ортографических проекций отдельных сторон объекта (вид спереди, вид сверху, вид сбоку).
В аксонометрических проекциях нормаль к картинной плоскости (а, следовательно, и направление проецирования) не совпадает ни с одной из координатных осей (рис. 6.3).
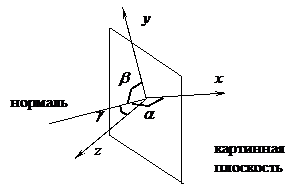
Рис. 6.3. Аксонометрическая проекция.
В зависимости от взаимного расположения картинной плоскости и осей координат выделяют следующие виды аксонометрических проекций:
а) триметрия – нормаль к картинной плоскости образует с координатными осями попарно различные углы (a ¹ b, b ¹ g, a ¹ g);
б) диметрия – два угла между нормалью к картинной плоскости и координатными осями равны;
в) изометрия – все три угла между нормалью к картинной плоскости и координатными осями равны (a = b = g).
|
|
|

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!