Метод вариации постоянных
Рассмотрим теперь метод решения линейных неоднородных дифференциальных уравнений 2-го порядка  с постоянными коэффициентами. Как было ранее, вначале необходимо найти
с постоянными коэффициентами. Как было ранее, вначале необходимо найти  для соответствующего однородного уравнения, а затем определить
для соответствующего однородного уравнения, а затем определить  . Будем его искать в той же форме, что и
. Будем его искать в той же форме, что и  , но
, но  и
и  будем считать функциями, то есть будем искать частное решение в виде
будем считать функциями, то есть будем искать частное решение в виде  .
.
Попытаемся определить эти функции. Для этого подставим  в исходное уравнение. Найдем вначале его первую производную:
в исходное уравнение. Найдем вначале его первую производную:
 .
.
Так как  и
и  никак не определены, будем считать их такими, что
никак не определены, будем считать их такими, что  . Тогда
. Тогда  . Вычислим теперь вторую производную:
. Вычислим теперь вторую производную:  . Подставим предполагаемое частное решение и его производные в уравнение:
. Подставим предполагаемое частное решение и его производные в уравнение:

В полученном выражении сумма во второй и третьей скобках равна нулю, так как вместо неизвестной функции подставлены частные решения соответствующего однородного уравнения. Поэтому уравнение приобретет вид:  .
.
В результате получена система из двух уравнений для определения  и
и  :
:

Чтобы получить решение данной системы составим ее определитель  , который не равен нулю, так как
, который не равен нулю, так как 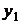 и
и 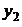 фундаментальная система решений соответствующего однородного уравнения. Таким образом,
фундаментальная система решений соответствующего однородного уравнения. Таким образом,  и
и  вычисляются однозначно. Находя затем их первообразные, определяем
вычисляются однозначно. Находя затем их первообразные, определяем  и
и  . При интегрировании константы к первообразным не добавляют, так как в ответе уже есть две константы
. При интегрировании константы к первообразным не добавляют, так как в ответе уже есть две константы  и
и  .
.
Линейное неоднородное дифференциальное уравнение второго порядка со специальной правой частью (ЛНДУ)
 , где
, где  .
.
Общее решение ЛНДУ  , где
, где
| №
| Вид правой части
| Корни характеристического уравнения
| Вид частного решения 
|
| 1.
| а)  б)
б) 
| Число 0 не является корнем характеристического уравнения
| 
|
Число 0 является корнем характеристического уравнения кратности 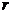
| 
|
| 2.
| а)  ,
(α − действительное)
б) ,
(α − действительное)
б)  ,
(α − действительное) ,
(α − действительное)
| Число α не является корнем характеристического уравнения
| 
|
Число α является корнем характеристического уравнения кратности 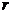
| 
|
| 3.
| а)  б)
б) 
| Числа  не являются корнями характеристического уравнения не являются корнями характеристического уравнения
| 
|
Числа  являются корнями характеристического уравнения кратности являются корнями характеристического уравнения кратности 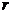
| 
|
| 4.
| а)  б)
б) 
| Числа  не являются корнями характеристического уравнения не являются корнями характеристического уравнения
| 
|
Числа  являются корнями характеристического уравнения кратности являются корнями характеристического уравнения кратности 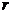
| 
|
Метод вариации постоянных
Рассмотрим теперь метод решения линейных неоднородных дифференциальных уравнений 2-го порядка  с постоянными коэффициентами. Как было ранее, вначале необходимо найти
с постоянными коэффициентами. Как было ранее, вначале необходимо найти  для соответствующего однородного уравнения, а затем определить
для соответствующего однородного уравнения, а затем определить  . Будем его искать в той же форме, что и
. Будем его искать в той же форме, что и  , но
, но  и
и  будем считать функциями, то есть будем искать частное решение в виде
будем считать функциями, то есть будем искать частное решение в виде  .
.
Попытаемся определить эти функции. Для этого подставим  в исходное уравнение. Найдем вначале его первую производную:
в исходное уравнение. Найдем вначале его первую производную:
 .
.
Так как  и
и  никак не определены, будем считать их такими, что
никак не определены, будем считать их такими, что  . Тогда
. Тогда  . Вычислим теперь вторую производную:
. Вычислим теперь вторую производную:  . Подставим предполагаемое частное решение и его производные в уравнение:
. Подставим предполагаемое частное решение и его производные в уравнение:

В полученном выражении сумма во второй и третьей скобках равна нулю, так как вместо неизвестной функции подставлены частные решения соответствующего однородного уравнения. Поэтому уравнение приобретет вид:  .
.
В результате получена система из двух уравнений для определения  и
и  :
:

Чтобы получить решение данной системы составим ее определитель  , который не равен нулю, так как
, который не равен нулю, так как 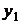 и
и 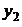 фундаментальная система решений соответствующего однородного уравнения. Таким образом,
фундаментальная система решений соответствующего однородного уравнения. Таким образом,  и
и  вычисляются однозначно. Находя затем их первообразные, определяем
вычисляются однозначно. Находя затем их первообразные, определяем  и
и  . При интегрировании константы к первообразным не добавляют, так как в ответе уже есть две константы
. При интегрировании константы к первообразным не добавляют, так как в ответе уже есть две константы  и
и  .
.
Линейное неоднородное дифференциальное уравнение второго порядка со специальной правой частью (ЛНДУ)
 , где
, где  .
.
Общее решение ЛНДУ  , где
, где
| №
| Вид правой части
| Корни характеристического уравнения
| Вид частного решения 
|
| 1.
| а)  б)
б) 
| Число 0 не является корнем характеристического уравнения
| 
|
Число 0 является корнем характеристического уравнения кратности 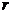
| 
|
| 2.
| а)  ,
(α − действительное)
б) ,
(α − действительное)
б)  ,
(α − действительное) ,
(α − действительное)
| Число α не является корнем характеристического уравнения
| 
|
Число α является корнем характеристического уравнения кратности 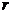
| 
|
| 3.
| а)  б)
б) 
| Числа  не являются корнями характеристического уравнения не являются корнями характеристического уравнения
| 
|
Числа  являются корнями характеристического уравнения кратности являются корнями характеристического уравнения кратности 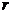
| 
|
| 4.
| а)  б)
б) 
| Числа  не являются корнями характеристического уравнения не являются корнями характеристического уравнения
| 
|
Числа  являются корнями характеристического уравнения кратности являются корнями характеристического уравнения кратности 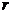
| 
|



 с постоянными коэффициентами. Как было ранее, вначале необходимо найти
с постоянными коэффициентами. Как было ранее, вначале необходимо найти  для соответствующего однородного уравнения, а затем определить
для соответствующего однородного уравнения, а затем определить  . Будем его искать в той же форме, что и
. Будем его искать в той же форме, что и  , но
, но  и
и  будем считать функциями, то есть будем искать частное решение в виде
будем считать функциями, то есть будем искать частное решение в виде  .
. .
. и
и  никак не определены, будем считать их такими, что
никак не определены, будем считать их такими, что  . Тогда
. Тогда  . Вычислим теперь вторую производную:
. Вычислим теперь вторую производную:  . Подставим предполагаемое частное решение и его производные в уравнение:
. Подставим предполагаемое частное решение и его производные в уравнение:
 .
. и
и  :
:
 , который не равен нулю, так как
, который не равен нулю, так как 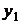 и
и 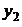 фундаментальная система решений соответствующего однородного уравнения. Таким образом,
фундаментальная система решений соответствующего однородного уравнения. Таким образом,  , где
, где  .
. , где
, где
 б)
б) 
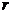

 ,
(α − действительное)
б)
,
(α − действительное)
б) 

 б)
б)  не являются корнями характеристического уравнения
не являются корнями характеристического уравнения


 б)
б)  не являются корнями характеристического уравнения
не являются корнями характеристического уравнения





