Лабораторная работа № 6. Сечения конуса плоскостями

Конические сечения – плоские кривые, которые получаются пересечением прямого кругового конуса плоскостью.

За исключением вырожденных случаев, коническими сечениями являются эллипсы, гиперболы или параболы. С точки зрения аналитической геометрии коническое сечение представляет собой геометрическое место точек, удовлетворяющих уравнению второго порядка.

Эллипс образуется, когда секущая плоскость пересекает все образующие конуса в точках одной его полости; парабола – когда секущая плоскость параллельна одной из касательных плоскостей конуса; гипербола – когда секущая плоскость пересекает обе полости конуса.

Существуют и вырожденные случаи конических сечений. Они появляются в тех случаях, когда секущая плоскость проходит через вершину конуса.

Если наклон плоскости к оси конуса больше, чем наклон образующей к оси, то сечением является точка – вершина конуса.

Если эти углы совпадают, то есть секущая плоскость касается конуса, то коническим сечением будет одна прямая.

Наконец, в случае, когда угол наклона секущей плоскости меньше, она пересекает конус по двум прямым.

1. Изучая конические сечения как пересечения плоскостей и конусов, древнегреческие математики рассматривали их и как траектории точек на плоскости.

Эллипс можно определить как геометрическое место точек, сумма расстояний от которых до двух заданных точек постоянна; параболу – как геометрическое место точек, равноудаленных от заданной точки и заданной прямой; гиперболу – как геометрическое место точек, разность расстояний от которых до двух заданных точек постоянна.

Эти определения конических сечений как плоских кривых подсказывают и способ их построения с помощью натянутой нити.

 

Эллипс. Если концы нити заданной длины закреплены в точках F₁ и F₂, то кривая, описываемая острием карандаша, скользящим по туго натянутой нити, имеет форму эллипса. Точки F₁ и F₂ называются фокусами эллипса, а отрезки V₁V₂ и v₁v₂ между точками пересечения эллипса с осями координат – большой и малой осями. Если точки F₁ и F₂ совпадают, то эллипс превращается в окружность.

Гипербола. При построении гиперболы точка P, острие карандаша, фиксируется на нити, которая свободно скользит по шпенькам, установленным в точках F₁ и F₂, как показано на рисунке (а). Расстояния подобраны так, что отрезок PF₂ превосходит по длине отрезок PF₁ на фиксированную величину, меньшую расстояния F₁F₂. При этом один конец нити проходит под шпеньком F₁ и оба конца нити проходят поверх шпенька F₂. (Острие карандаша не должно скользить по нити, поэтому его нужно закрепить, сделав на нити маленькую петлю и продев в нее острие.) Одну ветвь гиперболы (PV₁Q) мы вычерчиваем, следя за тем, чтобы нить оставалась все время натянутой, и потягивая оба конца нити вниз за точку F₂, а когда точка P окажется ниже отрезка F₁F₂, придерживая нить за оба конца и осторожно отпуская ее. Вторую ветвь гиперболы мы вычерчиваем, предварительно поменяв шпеньки F₁ и F₂.

Ветви гиперболы приближаются к двум прямым, которые пересекаются между ветвями. Эти прямые, называемые асимптотами гиперболы, строятся как показано на рисунке (б). Угловые коэффициенты этих прямых равны , где – отрезок биссектрисы угла между асимптотами, перпендикулярной отрезку F₂F₁; отрезок v₁v₂ называется сопряженной осью гиперболы, а отрезок V₁V₂ – ее поперечной осью. Таким образом, асимптоты являются диагоналями прямоугольника со сторонами, проходящими через четыре точки v₁, v₂, V₁, V₂ параллельно осям. Чтобы построить этот прямоугольник, необходимо указать местоположение точек v₁ и v₂. Они находятся на одинаковом расстоянии, равном от точки пересечения осей O. Эта формула предполагает построение прямоугольного треугольника с катетами Ov₁ и V₂O и гипотенузой F₂O.

Если асимптоты гиперболы взаимно перпендикулярны, то гипербола называется равнобочной. Две гиперболы, имеющие общие асимптоты, но с переставленными поперечной и сопряженной осями, называются взаимно сопряженными.

Парабола. Фокусы эллипса и гиперболы были известны еще Аполлонию, но фокус параболы, по-видимому, впервые установил Папп (вторая половина III в.), определивший эту кривую как геометрическое место точек, равноудаленных от заданной точки (фокуса) и заданной прямой, которая называется директрисой. Построение параболы с помощью натянутой нити, основанное на определении Паппа, было предложено Исидором Милетским (VI в.).

Расположим линейку так, чтобы ее край совпал с директрисой, и приложим к этому краю катет AC чертежного треугольника ABC. Закрепим один конец нити длиной AB в вершине B треугольника, а другой – в фокусе параболы F. Натянув острием карандаша нить, прижмем острие в переменной точке P к свободному катету AB чертежного треугольника. По мере того, как треугольник будет перемещаться вдоль линейки, точка P будет описывать дугу параболы с фокусом F и директрисой так как общая длина нити равна AB, отрезок нити прилегает к свободному катету треугольника, и поэтому оставшийся отрезок нити PF должен быть равен оставшейся части катета AB, то есть PA. Точка пересечения V параболы с осью называется вершиной параболы, прямая, проходящая через F и V, – осью параболы. Если через фокус провести прямую, перпендикулярную оси, то отрезок этой прямой, отсекаемый параболой, называется фокальным параметром. Для эллипса и гиперболы фокальный параметр определяется аналогично.

Задание. Сконструируйте приспособление для изображения кривых второго порядка, используя описанные выше инструменты и принципы. Применяя приспособление, заготовьте по три шаблона эллипсов, параболы, ветви гиперболы различных размеров из плотной бумаги.

2. Конус изображается эллипсом и парой касательных к нему, проведенных из одной точки, которая будет изображением вершины конуса.Следует заметить, что касательные к эллипсу, изображающие контурные образующие эллипса, не следует изображать касающимися в диаметрально противоположных точках, так как при таком изображении конус будет изображаться в виде треугольника. Постройте сечение конуса плоскостью, проходящей через точки K, L, М сначала методом следов, затем методом внутреннего проектирования. Каждый чертёж выполните на листе формата А4, а затем «скопируйте конечный результат» на данные чертежи.

3. Внеаудиторное задание. (1) Решить задачи №№ 21-24 из пособия Игошин В.И. Тетрадь по геометрии для 11 класса. Круглые тела и их сечения, объёмы, площади поверхностей. – Саратов, 1998. – 64 с. (2) В среде «1С: Математический конструктор» создайте динамическую модель построения эллипса.

Лабораторная работа № 7. Конфигурации многогранников и тел вращения (вписанные и описанные тела)

1. Сформулируйте свойства/признаки вписанных/описанных тел. Результаты оформите в таблицу (заполните таблицу).

Чертёж	Условие	Заключение
	Если на сфере лежат окружности оснований цилиндра, то	сфера описана около цилиндра
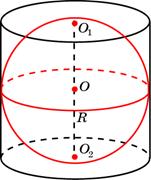
	В цилиндр можно вписать сферу, если высота цилиндра равна   Центром вписанной в цилиндр сферы будет точка   Радиус вписанной в цилиндр сферы будет равен	диаметру его основания. являющаясясерединой отрезка, соединяющего центры оснований цилиндра.   радиусу окружности основания цилиндра.
	Если на сфере лежит окружность основания конуса, то	сфера описана около конуса
Около конуса всегда можно описать	сферу. Ее центр находится на высоте конуса, а радиус равен радиусу окружности, описанной около треугольника, являющимся осевым сечением конуса.

 

Чертёж	Условие	Заключение
	В любой конус (прямой, круговой) можно вписать	сферу. Ее центр находится на высоте конуса, а радиус равен радиусу окружности, вписанной в треугольник, являющийся осевым сечением конуса.
	Сфера проходит через все вершины многогранника	сфера описана около многогранника
	Для того чтобы около многогранника можно было описать сферу, необходимо (но недостаточно), чтобы около любой его грани	можно было описать окружность.

 

Чертёж	Условие	Заключение
	Центр описанной около многогранникасферы лежит в плоскостях, перпендикулярных	ребрам многогранника, проходящих через их середины; а также на прямых, перпендикулярных граням многогранника, проходящих через центры описанных около граней окружностей.
	Радиус описанной около многогранникасферы равен радиусу сферы, проходящей через любые четыре, не лежащие в одной плоскости	вершины многогранника.
	Около любой треугольной пирамиды можно описать	сферу.
	Около любой правильной пирамиды можно описать	сферу.
Чертёж	Условие	Заключение
	Центром сферы, описанной около пирамиды, будет точка пересечения плоскостей,	проходящих через середины рёбер пирамиды перпендикулярно им.
Центр сферы, описанной около пирамиды, лежит в точке пересечения прямой	перпендикулярной основанию пирамиды, проходящей через центр описанной около основания окружности и плоскости, перпендикулярной любому боковому ребру, проведённой через середину этого ребра.
	Центр сферы, описанной около пирамиды, высота которой проектируется в центр описанной окружности вокруг основания, лежит	на середине диаметра, проведённого через центр этой окружности, перпендикулярно ей.
	Около n-угольной пирамиды можно описать сферу тогда и только тогда, когда	около ее основания можно описать окружность.
Если около основания пирамиды можно описать окружность, то около этой пирамиды можно описать	сферу.
	В любую правильную пирамиду можно вписать	сферу.

 

Чертёж	Условие	Заключение
	В любой тетраэдр	можно вписать сферу.
	В пирамиду можно вписать сферу тогда, когда биссекторные плоскости внутренних двугранных углов пирамиды	пересекаются в одной точке. Эта точка будет центром сферы.
	Если боковые грани пирамиды одинаково наклонены к основанию, то в такую пирамиду можно вписать	сферу.
	Около призмы можно описать сферу тогда и только тогда, когда	призма прямая и около ее основания можно описать окружность.
Чертёж	Условие	Заключение
	Для того чтобы в призму можно было вписать сферу, необходимо и достаточно, чтобы в перпендикулярное сечение призмы можно было	вписать окружность и чтобы высота призмы была равна диаметру этой окружности.
	В правильную призму можно вписать сферу тогда и только тогда, когда ее высота равна	диаметру окружности, вписанной в основание.
	Около цилиндра всегда можно описать	сферу. Ее центром будет точка O,являющаяся серединой отрезка, соединяющего центры оснований O 1 и O 2цилиндра. Радиус сферы R вычисляется по формуле где h – высота цилиндра, r – радиус окружности основания.
	Если сфера касается граней двугранного угла, то ее центр	лежит на полуплоскости, делящей этот двугранный угол на два равных двугранных угла.

 

Чертёж	Условие	Заключение
	Призма называется вписанной в цилиндр (а цилиндр – описанным около призмы), если	основания призмы вписаны в основания цилиндра.
Для того чтобы около призмы можно было описать цилиндр, необходимо и достаточно, чтобы	призма была прямая и около ее основания можно было описать окружность.
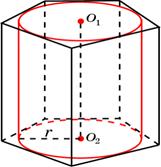
	Цилиндр называется вписанным в призму (а призма – описанной около цилиндра), если	основания цилиндра вписаны в основания призмы.
Для того чтобы в призму можно было вписать цилиндр, необходимо, чтобы	призма была прямая, и в ее основание можно было вписать окружность.
Радиус основания цилиндра вписанного в призму равен	радиусу окружности, вписанной в основание призмы
Высота цилиндра вписанного в призму равна	высоте призмы.
	Пирамида называется вписанной в конус (а конус – описанным около пирамиды), если	вершина пирамиды совпадает с вершиной конуса, а основание вписано в основание конуса

 

Чертёж	Условие	Заключение
	Для того чтобы около пирамиды можно было описать конус, необходимо и достаточно, чтобы боковые ребра пирамиды	имели равные длины.
	Пирамида называется описанной около конуса (а конус – вписанным в пирамиду),	если вершина пирамиды совпадает с вершиной конуса, а основание пирамиды описано около основания конуса.
	Для того чтобы в пирамиду можно было вписать конус, необходимо и достаточно, чтобы	в основание пирамиды можно было вписать окружность, а основание высоты пирамиды было центром этой окружности.
Вписать конус в пирамиду можно только тогда, когда апофемы	пирамиды равны между собой

 

Чертёж	Условие	Заключение
	Пирамида называется вписанной в цилиндр, если	ее вершина пирамиды принадлежит одному основанию цилиндра, а основание вписано в другое основание цилиндра
	В цилиндр можно вписать пирамиду, основание которой	можно вписать в окружность, причём высоты пирамиды цилиндра должны быть равны
	Цилиндр называется вписанным в пирамиду, если	одно его основание совпадает с окружностью вписанной в сечение пирамиды плоскостью, параллельной основанию, а другое основание принадлежит основанию пирамиды.

 

Чертёж	Условие	Заключение
	В пирамиду можно вписать цилиндр только в том случае, если в основании пирамиды –	многоугольник, в который можно вписать окружность.
	В усеченный конус можно вписать сферу, если в его осевое сечение	можно вписать окружность. Радиус этой окружности будет равен радиусу вписанной сферы.
В усеченный конус можно вписать сферу в том и только в том случае, если его образующая	равна сумме радиусов оснований.
	Около любой правильной усеченной пирамиды можно (достаточное условие) описать	сферу.
	В правильную усеченную пирамиду можно вписать сферу в том и только в том случае, если	апофема пирамиды равна сумме апофем оснований.

 

2. 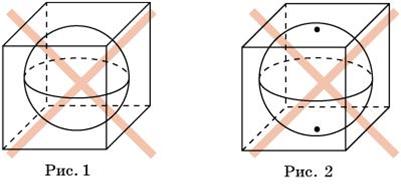Рассмотрим теперь вопрос об изображении комбинаций многогранников и тел вращения. Начнем с куба и сферы. Одной из распространенных ошибок изображения сферы, вписанной в куб, является изображение, показанное на рисунке 1. Здесь сразу несколько ошибок. Первая связана с неверным изображением точек касания. Точки касания должны располагаться не на окружности, ограничивающей изображение сферы, а внутри нее. Так, например, точки касания верхней и нижней граней куба должны располагаться в полюсах сферы. Эту ошибку можно исправить, несколько увеличив размеры вписанной сферы, как показано на рисунке 2. Здесь как будто точки касания верхней и нижней граней куба расположены в полюсах сферы, однако это изображение также не является верным. Ошибка рисунков 1 и 2 состоит в том, что для изображения сферы и куба использованы разные проекции. Сфера изображена в ортогональной проекции, а куб нет. На одном изображении этого делать нельзя. Если сфера изображается в ортогональной проекции, то и куб должен изображаться в ортогональной проекции.

Для построения правильного изображения сферы, вписанной в куб, сначала изобразим сферу с экватором и полюсами (рис. 3). Затем, опишем около экватора квадрат и построим его изображение. Это можно сделать следующим образом. Отметим на эллипсе, изображающем экватор какую-нибудь точку A и проведем касательную a к эллипсу в этой точке. Через точку A и центр эллипса O проведем прямую, и ее точку пересечения с эллипсом обозначим B. Через точку B проведем прямую b, параллельную a. Она также будет касательной к эллипсу. Построим диаметр CD, сопряженный диаметру AB эллипса и через точки C и D проведем прямые c и d, параллельные AB. Они будут касательными к эллипсу. Параллелограмм PQRS будет искомым изображением квадрата, описанного около экватора.

Через вершины параллелограмма проведем прямые, параллельные оси SN сферы и отложим на них в обе стороны отрезки, равные ON = OS. Получим вершины верхнего и нижнего оснований куба, описанного около сферы. Соединяя теперь соответствующие вершины верхнего и нижнего оснований, получим остальные ребра искомого куба (рис. 4).

Изображение куба, описанного около данной сферы, полностью определяется начальным выбором точки A. Выбирая различным образом эту точку можно получать различные изображения куба, описанного около сферы.

Задание. Постройте ещё два изображения куба, выбрав другие положения точки А.

Аналогичным образом строится изображение правильной треугольной призмы, описанной около сферы (рис. 5). Сначала строим изображение правильного треугольника, описанного около экватора. Для этого выбираем точку касания A и проводим через нее касательную a. Через точку A и центр эллипса проводим прямую и откладываем на ней отрезок OB = 2OA. Через точку B проводим касательные b и c к эллипсу. Прямые a, b и c образуют искомый треугольник, описанный около эллипса (рис. 6). Через вершины этого треугольника проведем прямые, параллельные оси SN сферы и отложим на них в обе стороны отрезки, равные ON = OS. Получим вершины верхнего и нижнего оснований призмы, описанной около сферы. Соединяя теперь соответствующие вершины верхнего и нижнего оснований, получим остальные ребра искомой призмы (рис. 5).

Аналогичным образом строится изображение пирамиды с вписанной в нее сферой (рис. 7). В случае, если сфера вписана в правильный тетраэдр (рис. 8), нужно учитывать, что центр сферы делит высоту пирамиды в отношении 3:1 считая от вершины. На рисунке 9 изображена сфера с вписанным в нее кубом. На рисунке 10 изображена сфера с вписанным в нее правильным тетраэдром.

Задание. Опишите этапы построения этих изображений.

3. Упражнения.

– Изобразите правильную шестиугольную призму, описанную около сферы.

– Изобразите правильную шестиугольную пирамиду, описанную около сферы.

– Изобразите конус, описанный около сферы.

– Изобразите сферу, описанную около правильной шестиугольной призмы.

– Изобразите сферу, описанную около правильной четырехугольной пирамиды.

– Изобразите октаэдр, вписанный в сферу.

– Изобразите сферу, описанную около цилиндра.

– Изобразите сферу, описанную около конуса.

– По данному изображению конуса постройте: а) центр вписанной сферы; б) центр описанной сферы.

4. Постройте геометрическую модель задачи и приведите решение этой задачи: В основании прямой призмы лежит выпуклый четырёхугольник ABCD, у которого AD = 8 cм, CD = 12 cм,Ð В = 120°, Ð D =60°, а боковое ребро имеет длины 10 см. Докажите, что около этой призмы можно описать сферу и найдите её радиус.

5. Внеаудиторное (индивидуальное) задание.

(1) Решить задачи из пособия Игошин В.И. Тетрадь по геометрии для 11 класса. Круглые тела и их сечения, объёмы, площади поверхностей. – Саратов, 1998. – 64 с.

Вариант

Задачи №

Вариант

Задачи №

9б

36а

48а

118а

36а

58б

64в

83а

9в

36б

48б

83а

36б

64а

9б

102а

64б

9в

54б

71б

102б

54б

64в

102в

106в

118д

9б

102г

106б

118г

9в

48б

64а

83б

106а

118в

58б

71б

83б

9б

48а

64б

83а

118б