ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Федеральное государственное образовательное учреждение
высшего профессионального образования
«ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ»
Семестровый курс лекций по дисциплине "Методы обработки биомедицинских сигналов и данных"
Работу выполнил
К.т.н., доцент Сахаров В.Л.
(должность, звание, ФИО)
Таганрог
Лекция 1. Основные типы сигналов. Общие понятия теории дискретных линейных систем. Некоторые понятия теории случайных процессов.
ОСНОВНЫЕ ТИПЫ СИГНАЛОВ
К основным типам сигналов относятся аналоговый, дискретный и цифровой. Аналоговым называется сигнал, непрерывный во времени и по состоянию. Это означает, что сигнал описывается непрерывной (или кусочно-непрерывной) функцией x(t), причем и аргумент, и сама функция могут принимать любые значения из некоторых:  .
.
Дискретным называется сигнал, дискретный во времени и непрерывный по состоянию. (рис. 1) Он описывается решетчатой функцией x(nT), где n – номер отсчета, n = 0, 1, 2, 3 … Интервал T называется периодом дискретизации, а обратную величину  - частотой дискретизации.
- частотой дискретизации.
Цифровым называется сигнал, дискретный как во времени, так и по состоянию. Сигналы этого типа также описываются решетчатой функцией x (nT), однако могут принимать только конечное число значений из некоторого конечного интервала  . Эти значения называются уровнями квантования, а соответствующие функции – квантованными.
. Эти значения называются уровнями квантования, а соответствующие функции – квантованными.
ОБЩИЕ ПОНЯТИЯ Теории дискретных линейных систем

Рис.1
Теория дискретных линейных систем связана с описанием и обработкой временных и частотных последовательностей.
При переходе из аналогового представления в цифровое отмечаются цифровые отсчеты на данном сигнале, которые и будут представлять собой цифровой сигнал. Процедура преобразования аналогового сигнала в цифровой называется дискретизаций. Основными параметрами дискретизации являются:
- интервал  между двумя соседними цифровыми отсчетами, называемый интервалом дискретизации;
между двумя соседними цифровыми отсчетами, называемый интервалом дискретизации;
- значение цифрового отсчета, соответствующее его амплитуде 
 , где
, где  -конечные отсчеты, между которыми рассматривается данный сигнал.
-конечные отсчеты, между которыми рассматривается данный сигнал.
Цифровой сигнал представляет собой массив значений амплитуд, заданный в определенной области (N1,N2) c определенным интервалом дискретизации  .
.
Каждое отдельное значение цифрового сигнала называется цифровым отсчетом. Каждый цифровой отсчет характеризуется разрядностью его представления. В зависимости от используемого АЦП количество разрядов цифрового сигнала в современных системах может колебаться от 1 до 256. Разрядность определяет максимально возможную амплитуду представляемого сигнала, которая определяется соотношением 2n-1, где n-количество разрядов.
Интервал дискретизации зависит от частоты дискретизации системы:

Интервал дискретизации для цифровых сигналов может быть равномерным или неравномерным.
Корреляционный анализ
Смысл корреляционного анализа состоит в количественном измерении степени сходства различных сигналов. Имеются понятия автокорреляционной функции и взаимно корреляционной функции.
Автокорреляционная функция
Для определения автокорреляционной функции (АКФ) используется следующее соотношение:
 (2.1)
(2.1)
АКФ показывает степень сходства между сигналом и его сдвинутой копией.
В некоторых случаях в выражении (2.1) для АКФ нормируют входные последовательности следующим образом:
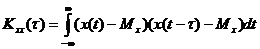 , где (2.2)
, где (2.2)
 исследуемый сигнал,
исследуемый сигнал,
 сигнал, сдвинутый на интервал времени
сигнал, сдвинутый на интервал времени  ,
,
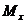 - мат. ожидание
- мат. ожидание 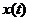 .
.
Формула для расчета АКФ дискретного сигнала:
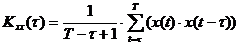 , где
, где  , (2.3)
, (2.3)
Т- интервал времени анализируемого участка сигнала.
Свойства АКФ:
1) АКФ является четной функцией  ;
;
2) Абсолютное значение АКФ при любом  не может превышать ее значение при
не может превышать ее значение при 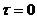 , т.е. ее максимальное значение при
, т.е. ее максимальное значение при 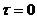 .
.
3) Для АКФ справедливо соотношение:
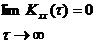

Физически это соотношение объясняется тем, что случайные процессы имеют конечное время корреляции. Использование АКФ является наиболее мощным средством выделения гармонических колебаний в процессе.
Примеры АКФ:
 Данный вид АКФ говорит о том, что процесс не имеет ярко выраженной гармонической компоненты.
Данный вид АКФ говорит о том, что процесс не имеет ярко выраженной гармонической компоненты.
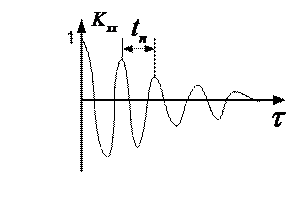
Свойственна процессам, которые сильно связаны между собой.
Если на АКФ имеются не сильно затухающие гармонические колебания, это значит, что процесс имеет постоянную гармоническую составляющую, период которой равен периоду колебания корреляционной функции.
Другие вариации графиков АКФ показывают степень наличия гармонической составляющей в процессе. Если график ближе к колебательному процессу, то в исследуемом сигнале имеются гармонические составляющие. Если ближе к экспоненциальной затухающей кривой, то гармонические составляющие слабо выражены.
Поскольку на основе визуальной оценки графика АКФ нельзя получить точную математическую оценку процесса, то были получены числовые величины характеризующие АКФ. К ним относятся:
1) Средняя частота (средний период) гармонических колебаний:
 ,
,
 интервал времени между двумя положительными экстремумами на АКФ,
интервал времени между двумя положительными экстремумами на АКФ,
N- количество таких интервалов.
2) Периодичность процесса – это коэффициент отношения мощности периодической (гармонической) составляющей к мощности случайной составляющей АКФ. Данный коэффициент определяется следующим образом:
· Производится измерение амплитуд каждого колебания АКФ от пика до пика;
· Вычисляется средняя величина амплитуды колебания:

· Определяется половина средней амплитуды, которая считается как средняя амплитуда периодической составляющей АКФ:

· Определяется разница между максимальным значением АКФ (при 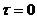 ) и вычисленным средним значением амплитуды периодической составляющей:
) и вычисленным средним значением амплитуды периодической составляющей:
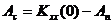
Эта амплитуда считается амплитудой случайных составляющих.
· Коэффициент периодичности определяется как отношение:
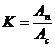
3) Устойчивость периодики определяется по величине задержки, при которой амплитуда периодических колебаний на АКФ уменьшилась на 10% от максимальной.
Спектральный анализ
С помощью спектрального анализа можно характеризовать частотный состав исследуемого временного ряда. Математической основой, которая связывает временной сигнал с его представлением в частотной области, является преобразование Фурье. Это преобразование играет важную роль не только как инструмент получения спектрального состава сигнала, но также как необходимый промежуточный этап при вычислении некоторых характеристик.
Преобразование Фурье и его основные свойства
Общий вид преобразования Фурье для непрерывных сигналов:
 , где (2.6)
, где (2.6)
 временной ряд (исследуемый сигнал),
временной ряд (исследуемый сигнал),
j- мнимая единица,
f- частота,
t- интервал времени, на котором производится анализ.
Преобразование Фурье существует, если выполняется условие абсолютной интегрируемости функции x(t), т.е.:
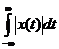 <
< 
Обратное преобразование Фурье – переход от частотной области к временной:
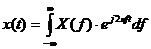
Непрерывно – дискретное преобразование Фурье применяется для дискретных сигналов:
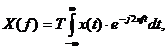 где
где
Т – участки временного ряда, имеющие непрерывную характеристику.
Другая запись:
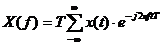
Дискретное преобразование Фурье используется для анализа дискретных сигналов, каковыми в большинстве своем являются медицинские сигналы. Формула для него имеет следующий вид:
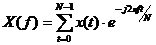 (2.7)
(2.7)
Обратное преобразование имеет следующий вид:
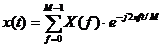 , где
, где
 временной ряд, представленный в виде дискретных отсчетов;
временной ряд, представленный в виде дискретных отсчетов;
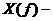 представленный в виде дискретных значений частотный ряд, отражающий спектральную оценку сигналов;
представленный в виде дискретных значений частотный ряд, отражающий спектральную оценку сигналов;
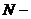 интервал времени, выраженный в количестве дискретных отсчетов, которые используются для анализа;
интервал времени, выраженный в количестве дискретных отсчетов, которые используются для анализа;
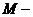 дискретно представленный частотный диапазон, в котором производится частотное представление сигналов.
дискретно представленный частотный диапазон, в котором производится частотное представление сигналов.
Формула перехода от логарифмического состава к тригонометрическому:
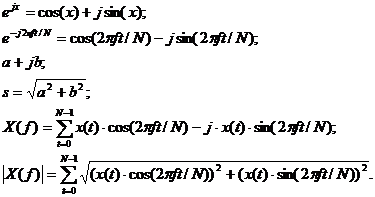
Лекция 3. Алгоритмы быстрого и дискретного преобразования Фурье. Функция спектральной плотности мощности. Алгоритмы ее определения. Функции когерентности и алгоритмы ее определения.
Быстрое преобразование Фурье
Вычисление преобразования Фурье по формуле (2.7) предполагает выполнение N2 раз операций сложения и умножения.
Основная идея быстрого преобразования Фурье состоит в разбиении исходного дискретного преобразования (2.7) на несколько частей, каждую из которых можно вычислить отдельно, а затем линейно просуммировать с остальными, чтобы получить исходное преобразование. Эти части малого размера можно разбить на еще меньшие, если считать длительность временного ряда равной N и использовать деление исходного преобразования (2.7) на каждом шаге на две части, то исходный временной ряд будет состоять из k частей так, что 2k =N. Тогда для выполнения вычислений потребуется log2N операций сложения и N/2 операций умножения на каждом шаге, что составляет приблизительно 4N*log2N операций. Это значительно меньше тех N2 операций, которые необходимы при вычислении по формуле (2.7). Эффективность алгоритма БПФ линейно возрастает с ростом длительности исходного сигнала.
Функция когерентности
Функция когерентности определяется следующим образом:

Функция когерентности является аналогом коэффициента корреляции в частотной области и отражает степень линейной взаимосвязи гармонических компонент рассматриваемых процессов. Чем ближе функция когерентности к 1 на конкретной частоте f, тем больше совпадения гармонических составляющих на этой частоте. Как правило, именно функция когерентности, а не взаимная спектральная плотность используется в практических приложениях для анализа связанности процессов в частотной области.
Лекция 4. Wavelet-анализ.
Вейвлет анализ широко используется для нестационарных случайных процессов. Он показал свою эффективность для решения широкого класса задач, связанных с подавлением шумов, сжатием больших объемов информации.
Вейвлет анализ, как и преобразование Фурье, состоит в вычислении корреляции между анализируемым временным рядом и базисной функцией преобразования. Вейвлет преобразование, состоящее в разложении ряда по базису, сконструированному из обладающих определенными свойствами функций, называется Вейвлетом (маленькая волна) посредством ее масштабных изменений и переносов. Каждая вейвлет функция базиса характеризуется определенным масштабом (частотой) и локализацией во времени. В отличие от преобразования Фурье вейвлет преобразование дает двумерную развертку одномерного процесса, при этом частота и время рассматриваются как независимые переменные. В результате появляется возможность анализировать свойства процесса одновременно в частотной и временной областях. В основе вейвлет преобразования лежит идея многомасштабного анализа, который заключается в последовательном огрублении исходной информации, содержащейся в процессе.
Данный подход позволяет выявлять локальные области процесса и классифицировать их по интенсивности; отслеживать динамику частотного состава процесса во времени. Операция огрубления исходной информации осуществляется путем сглаживания исходного ряда с помощью функции вейвлета  . Термин вейвлет обозначает локализованные во временной и частотной областях функции, обладающие следующими свойствами:
. Термин вейвлет обозначает локализованные во временной и частотной областях функции, обладающие следующими свойствами:
1) Вейвлет имеет среднее значение, равное нулю:
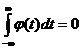 .
.
2) Ограниченность функции вейвлета, т.е. она быстро убывает при 
3) Автомодельность, т.е. при любых масштабных изменениях вейвлета его форма (количество экстремумов) не меняется.
Данные свойства определяют большой класс действительных и комплексных функций, которые являются вейвлетами. Вейвлет локализован сразу в двух областях: временной и частотной. Для осуществления вейвлет преобразования произвольного временного ряда x(t) необходимо предусмотреть возможность сдвигов функции вейвлета вдоль временной оси и масштабных преобразований в частотной области путем сжатия или растяжения исходного вейвлета. Такую возможность реализует базисная функция следующего вида:
 .
.
Соответственно, вейвлет преобразование сигнала имеет вид:
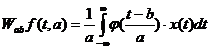 (4.1)
(4.1)
В этой формуле a и b являются действительными числами и определяют масштаб (величину обратно пропорциональную частоте) и временной сдвиг соответственно.
На основе этой базисной функции вейвлет преобразование временного ряда x(t) определенного на всей временной оси ( ) записывается в виде (4.1). В формуле (4.1) параметр «b» меняется в интервале от
) записывается в виде (4.1). В формуле (4.1) параметр «b» меняется в интервале от  до
до  , пробегая всю временную ось, т.е. всю временную область, на которой определена функция x(t). Параметр «a» меняется от 0 до
, пробегая всю временную ось, т.е. всю временную область, на которой определена функция x(t). Параметр «a» меняется от 0 до  . При использовании действительной функции вейвлета в результате преобразования получается двумерный массив коэффициентов W(a,b), а при применении комплексной функции вейвлета в результате получаются двумерные массивы модуля и фазы:
. При использовании действительной функции вейвлета в результате преобразования получается двумерный массив коэффициентов W(a,b), а при применении комплексной функции вейвлета в результате получаются двумерные массивы модуля и фазы:

Алгоритм вычисления коэффициента вейвлет преобразования по формуле (4.1) для каждой пары параметров «a» и «b» выглядит следующим образом:
1) растянуть вейвлет  в a раз по горизонтали в 1/a раз по вертикали;
в a раз по горизонтали в 1/a раз по вертикали;
2) сдвинуть вейвлет в точку  по оси времени;
по оси времени;
3) произвести вычисление вейвлета по (4.1) и усреднить значение полученной функции по ширине окна самого вейвлета;
Далее процедура повторяется для другой пары параметров «a» и «b» до тех пор, пока не будут рассчитаны вейвлет преобразования для всех значений «a» и «b». Полученные результаты Wab представляются на графике преобразования следующим образом:

Результат кодируется цветом. Два наиболее распространенных вейвлета, применяемых в медицинских целях называются Сомбреро и Вейвлет Морле.
 Вейвлет Морле
Вейвлет Морле
Сомбреро

Для дискретных сигналов формула расчета вейвлет-преобразования имеет вид:

 (4.2)
(4.2)

 сигнал, представленный в виде дискретных цифровых отсчетов;
сигнал, представленный в виде дискретных цифровых отсчетов;

 вейвлет;
вейвлет;

 длительность окна вейвлет преобразования.
длительность окна вейвлет преобразования.
В медицинских целях вейвлет преобразование может применяться для сжатия исходных сигналов. В этом случае необходимо знать формулу обратного вейвлет преобразования, позволяющего восстановить исходный временной ряд:




 нормализующий коэффициент.
нормализующий коэффициент.
Лекция 5. Основные характеристики линейных дискретных систем. Введение в цифровые фильтры. Основные определения и классификация цифровых фильтров.
Основные понятия линейной дискретной системы.
Линейная система – система обладающая следующими свойствами:
1) Аддитивность: x = x1 +x2; F(x) = F(x1) + F(x2) т.е. реакция на сумму воздействий равна сумме реакций на каждое воздействие.
2) Однородностность: F(ax) = aF(x).
Линейная система называется дискретной, если воздействие и реакция представляют собой дисперсные сигналы, которые могут быть как вещественными, так и комплексными: x(nT)→Y(nT)

x(nT) ЛДС Y(nT)


Импульсной характеристикой h(nT) линейной дискретной системы (ЛДС) называется ее реакция на единичный цифровой импульс U0(nT) при нулевых начальных условиях. Нулевые начальные условия – отсутствие реакции при отсутствии воздействия. Импульсная характеристика это одна из основных характеристик ЛДС, т.к. с ее помощью легко определяется реакция на произвольное воздействие. При описании ЛДС во временной области, помимо импульсной используют переходную характеристику g(nT) т.е. реакция ЛДС на единичный цифровой скачок при нулевых начальных условиях.



 U(T) U(T)
U(T) U(T)

 U0
U0
Соотношение вход – выход отображает взаимосвязь между ее входным x(nT) и выходным Y(nT) сигналами, т.е. реакцию ЛДС на произвольное воздействие. Во временной области соотношение вход - выход описывается линейными уравнениями: 1) формулой свертки (5.1), если используется импульсная характеристика; 2) разностным уравнением, если не используется импульсная характеристика (5.2).
 (5.1)
(5.1)
Если известны параметры ЛДС, взаимосвязь между реакцией x(nT) и воздействием Y(nT) описывается разностным уравнением:
 (5.2)
(5.2)
где bi и ak - коэффициенты уравнения;
i и k – значения задержки для воздействия реакции;
M и N – константы определяющие порядок уравнения или порядок фильтра;
x((n– i)T) и y((n–k)T) – реакции и воздействия в соответствующие периоды дискретизации.
Введение в цифровые фильтры. Основные определения и классификация.
Под цифровыми фильтрами понимают любую цифровую систему или цепь, которая согласно заданному алгоритму y(n) =F(x'(n)) осуществляет извлечение цифрового сигнала x (n), либо его параметров, из действующей на входе системы смеси сигналов:
x'(n) = x(n)+ g(n), где x(n) – извлекаемый цифровой сигнал, g(n) – помеха. В соответствии с этим, под фильтром можно понимать амплитудные и фазовые корректоры, дифференциаторы, адаптивные фильтры и т.д.
Цифровой фильтр в узком понимании - частотная избирательная цепь, которая обеспечивает селекцию цифровых сигналов по частоте. К таким фильтрам относятся ФНЧ, ФВЧ, полосовой и режекторный.
x(n)+ g(n)  y(n)
y(n)

 F(x'(n))
F(x'(n))
Цифровые фильтры (ЦФ) делятся на 2 больших класса: нерекурсивные (БИХ) и рекурсивные (КИХ). Они могут быть реализованы аппаратно, программно или аппаратно – программно, что определяется местом назначения и целью расположения предполагаемого фильтра в системе. Аппаратная реализация подразумевает рациональное использование разнообразных функциональных блоков (сумматоров, умножителей и т.д.). Программная реализация подразумевает, что фильтр написан на каком – либо языке программирования (на языке высокого уровня для ПК или на языке ассемблера). Аппаратно – программная реализация подразумевает синтез двух первых методов.
Под проектированием цифрового фильтра понимают процесс, результатом которого является программа или цифровое устройство, отвечающее заданным требованиям и ограничениям. Процесс проектирования включает в себя следующие этапы:
1) Синтез, результатом которого является функциональная схема фильтра с рассчитываемыми коэффициентами. Процедура синтеза КИХ- и БИХ-фильтров существенно различаются, но имеют одинаковую последовательность действий:
a) Задание требований к фильтрам;
b) Решение задачи аппроксимации характеристик фильтра;
c) Конструирование функциональной схемы цифрового фильтра.
2) Выбор или разработка алгоритмов вычисления. Алгоритм зависит от метода реализации (с плавающей или фиксированной точкой), разрядности, возможности распараллеливания операций и т.д. Конечной целью этого этапа является обеспечение функционирования фильтра в реальном времени при минимальных потерях качества обработки сигналов;
3) Проверка работоспособности фильтра моделированием. Проверка подразумевает использование различных программных средств, позволяющих симулировать работу фильтра, и ее задача состоит в обнаружении и устранении возможных логических и других ошибок, а также испытаний сконструированного фильтра в заданных характеристиках, включая частотные, шумовые и временные;
4) Практическая реализация и отладка.
Лекция 6. Синтез цифровых фильтров и задание требований к цифровым фильтрам. Типы избирательных фильтров и задание требований к ним.
Синтез цифровых фильтров и задание требований к цифровым фильтрам
Требования к ЦФ могут формироваться как во временной, так и в частотной областях, что определяется назначением фильтра и областью его описания. Во временной области требования могут задаваться к импульсной или переходной характеристике. Согласованные фильтры целиком определяются импульсной характеристикой, а высокоскоростные системы весьма критичны к длительности переходных процессов и в подобных системах особые требования предъявляются к переходным характеристикам ЦФ. В частотной области требования могут предъявляться:
1) только к АЧХ без каких–либо ограничений на ФЧХ;
2) только к ФЧХ, когда важно сохранить фазовые особенности сигнала (такие устройства называют фазовыми корректорами);
3) одновременно к АЧХ и к ФЧХ.
Рассмотрим в качестве примера задание требований к частотно – избирательным ЦФ (ФНЧ, ФВЧ, полосовой, режекторный). Рассмотрим их АЧХ:
1)  ФНЧ
ФНЧ
2)  ФВЧ
ФВЧ
3)  Полосовой фильтр
Полосовой фильтр
4)  Режекторный фильтр
Режекторный фильтр
Вследствие физической невозможности реализации АЧХ таких фильтров необходимо задавать допуски для АЧХ, зависящие от ряда практических ограничений. Эти ограничения связаны прежде всего с назначением синтезированного ЦФ. Все ограничения и допуски составляют требования, предъявляемые к ЦФ. Требования включают в себя:
1) задание частоты дискретизации -  ;
;
2) задание типа избирательности фильтра;
3) задание требований к АЧХ - 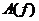 , или к характеристике ослабления
, или к характеристике ослабления  , представляют собой АЧХ, выраженных в логарифмическом масштабе. Их связь выражена:
, представляют собой АЧХ, выраженных в логарифмическом масштабе. Их связь выражена:

4) выбор метода аппроксимации АЧХ фильтра.
При задании требований следует помнить что:
- необходимо установить все граничные частоты фильтра только в основной полосе его рабочих частот:
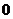 <
<  <
<  .
.
- требования к фильтрам не задаются в переходных областях избирательных фильтров.
- требования формулируются в виде допустимых отклонений от нормированной АЧХ и отображаются на диаграмме допусков.

- размерность 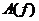 выражается в абсолютных единицах, размерность
выражается в абсолютных единицах, размерность  выражается в децибелах.
выражается в децибелах.
Типы избирательных фильтров и задание требований к ним
1. ФНЧ имеет три частотные полосы: полосу пропускания, полосу задерживания или ослабления и переходную полосу:

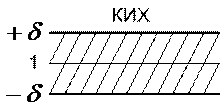

Полоса пропускания ограничивается частотой среза  . Ширина полосы пропускания
. Ширина полосы пропускания 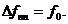
В соответствии с методом синтеза фильтров отклонение АЧХ от единицы в полосе пропускания задается симметрично и находится в пределе:
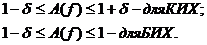
Для БИХ – фильтров задается только в одну сторону так, чтобы АЧХ не превышало 1.  максимально допустимое отклонение от 1.
максимально допустимое отклонение от 1.
Полоса задерживания лежит в пределах от граничных частот  до значения верхней максимально возможной частоты
до значения верхней максимально возможной частоты  . Ширина полосы задерживания
. Ширина полосы задерживания 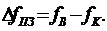 Допустимые отклонения АЧХ в полосе задерживания для КИХ-фильтров и БИХ-фильтров:
Допустимые отклонения АЧХ в полосе задерживания для КИХ-фильтров и БИХ-фильтров:

 максимально допустимое отклонение АЧХ от нуля.
максимально допустимое отклонение АЧХ от нуля.
Переходная полоса расположена между полосой пропускания и полосой задерживания. Ее ширина  , так как в этой полосе требования не задаются, то удовлетворительным окажется любое решение, если оно соответствует требованиям в полосе пропускания и полосе задержки.
, так как в этой полосе требования не задаются, то удовлетворительным окажется любое решение, если оно соответствует требованиям в полосе пропускания и полосе задержки.
2. ФВЧ, как и ФНЧ, имеет три частотные полосы, которые расположены в обратном относительно ФНЧ порядке. Полоса задерживания ФВЧ находится  . Ширина полосы задерживания
. Ширина полосы задерживания  .
.

Переходная полоса находится в пределе  , ширина
, ширина  . Полоса пропускания:
. Полоса пропускания:  , ширина
, ширина 
3. Полосовой фильтр характеризуется пятью частотными полосами:

 граничная частота ПЗ1, ширина ПЗ1
граничная частота ПЗ1, ширина ПЗ1 
 левая частота среза полосы пропускания;
левая частота среза полосы пропускания;
 правая частота среза ПП;
правая частота среза ПП;

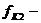 граничная частота ПЗ2;
граничная частота ПЗ2; 
Переходные полосы имеют ширину:

4. Режекторный фильтр характеризуется пятью полосами, из которых две полосы пропускания, одна полоса задерживания и две переходные полосы:


Синтез БИХ- фильтров
Синтез цифрового фильтра по заданным требованиям к его характеристикам сводится к решению задачи аппроксимации требуемой АЧХ фильтра, которая решается чисто математическими методами, в области, определяющей назначение фильтра.
Если аппроксимация производится в p-области, то получим аналоговый фильтр, а если в z- области, то цифровой фильтр.
При синтезе стандартных частотно избирательных БИХ- фильтров (ВЧ, НЧ, полосовой, режекторный) удобнее всего воспользоваться хорошо развитым аппаратом расчета аналоговых фильтров и методами преобразования аналоговых фильтров в цифровые, то есть переходов из p-области в z- область.
Такой синтез включает в себя:
□ выбор метода отображения р-области в z-область;
□ расчет аналогового фильтра по требованиям, заданным к цифровому фильтру;
□ применение к аналоговому фильтру выбранного метода отображения р-области в z-область.
Аналоговый фильтр, рассчитываемый по требованиям, заданным к цифровому фильтру, называется фильтром-прототипом.
Основными ограничениями для методов синтеза цифровых фильтров по прототипам являются:
1. сохранение существенных свойств амплитудно-частотной характеристики (АЧХ) прототипа в АЧХ цифрового фильтра;
2. устойчивый прототип должен быть преобразован в устойчивый цифровой фильтр.
Для преобразования аналогового фильтра в цифровой фильтр наиболее часто применяются два метода:
1. стандартное z- преобразование;
2. билинейное z- преобразование.
Фильтр Баттерворта.
Аппроксимирующий полином такого фильтра имеет вид:
 , где N – порядок фильтра
, где N – порядок фильтра
АЧХ такого фильтра является монотонной и в полосе пропускания и в полосе задерживания, а также характеризуется очень широкой переходной полосой.


Основное свойство фильтра Баттерворта — равенство амплитудно-частотной характеристики величине 0,707 на частоте среза — говорит о том, что процедура аппроксимации сосредотачивается на двух частотах: ω= 0 и ω=∞. Поэтому единственным параметром является порядок N, определяющий степень плоскости на указанных крайних частотах: чем выше порядок, тем более плоской оказывается АЧХ и тем более близкой становится она к желаемой характеристике как в полосе пропускания, так и в полосе задерживания.
При увеличении порядка фильтра возрастает коэффициент прямоугольности, то есть уменьшается переходная полоса. Чем выше порядок фильтра, тем более близкой к идеальной является АЧХ фильтра. Нули находятся на ω=±∞ (соответственно на z-плоскости в точке z =-1). Полюсы равномерно распределены на единичной окружности р-плоскости. Полюса рассчитываются по формуле
 , где k- номер рассчитываемого полюса.
, где k- номер рассчитываемого полюса.
Выводы:
· фильтры Баттерворта обладают максимально плоской АЧХ в полосе пропускания и монотонной в полосе задерживания;
· в полосе пропускания ФЧХ близка к линейной;
· фильтры Баттерворта применяются при необходимости сохранения соотношений составляющих сигнала по амплитуде и фазе.
Фильтр Чебышева
Чтобы получить достаточно крутую характеристику АЧХ в переходной области для фильтра Баттерворта необходимо использовать очень высокий порядок. Ту же характеристику в переходной полосе и при гораздо меньшем порядке, можно получить с помощью фильтров Чебышева, в которых ошибка аппроксимации равномерно распределена по полосе пропускания или по полосе задерживания. В зависимости от области, в которой минимизируется ошибка аппроксимации, различают фильтры Чебышева I и II рода.
Фильтр I рода в полосе пропускания имеет равноволновой характер аппроксимации АЧХ, а в полосе задерживания – оптимально плоский. Фильтр II рода в полосе задерживания имеет волновой характер аппроксимации, а в полосе пропускания – оптимально плоский.

АЧХ фильтра Чебышева I рода:

 , где
, где  ;
; 
Нули у фильтра Чебышева I рода не вычисляются, а для полюсов используется следующая формула:

Для фильтров Чебышева II рода используется следующий вид аппроксимирующего АЧХ полинома:

Полюса рассчитываются по формуле:

Нули рассчитываются по формуле:

Эллиптические фильтры
Они характеризуются равноволновой АЧХ как в полосе пропускания, так и в полосе задерживания; но более крутой характеристикой в переходной полосе при тех же порядках, что и в фильтре Чебышева.
Поэтому такие фильтры применяют в задачах, требующих высокой избирательности и не критичных к виду фазочастотной
характеристики, которая не является линейной.

 , где
, где  - эллиптический полином
- эллиптический полином 
Данный тип фильтра не так часто используется в связи со сложностью его расчета.
Фильтр Бесселя
|
|
|



 .
. - частотой дискретизации.
- частотой дискретизации. . Эти значения называются уровнями квантования, а соответствующие функции – квантованными.
. Эти значения называются уровнями квантования, а соответствующие функции – квантованными.
 между двумя соседними цифровыми отсчетами, называемый интервалом дискретизации;
между двумя соседними цифровыми отсчетами, называемый интервалом дискретизации;
 , где
, где  -конечные отсчеты, между которыми рассматривается данный сигнал.
-конечные отсчеты, между которыми рассматривается данный сигнал.
 (2.1)
(2.1)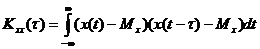 , где (2.2)
, где (2.2) исследуемый сигнал,
исследуемый сигнал, сигнал, сдвинутый на интервал времени
сигнал, сдвинутый на интервал времени  ,
,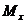 - мат. ожидание
- мат. ожидание 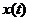 .
.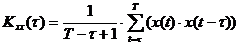 , где
, где  , (2.3)
, (2.3) ;
;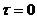 , т.е. ее максимальное значение при
, т.е. ее максимальное значение при 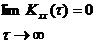

 Данный вид АКФ говорит о том, что процесс не имеет ярко выраженной гармонической компоненты.
Данный вид АКФ говорит о том, что процесс не имеет ярко выраженной гармонической компоненты.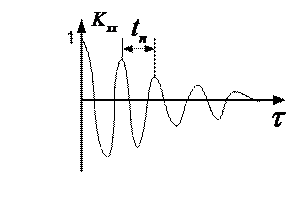
 ,
, интервал времени между двумя положительными экстремумами на АКФ,
интервал времени между двумя положительными экстремумами на АКФ,

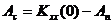
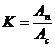
 , где (2.6)
, где (2.6)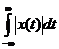 <
< 
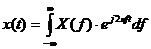
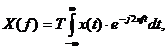 где
где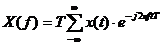
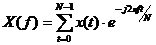 (2.7)
(2.7)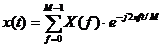 , где
, где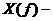 представленный в виде дискретных значений частотный ряд, отражающий спектральную оценку сигналов;
представленный в виде дискретных значений частотный ряд, отражающий спектральную оценку сигналов;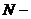 интервал времени, выраженный в количестве дискретных отсчетов, которые используются для анализа;
интервал времени, выраженный в количестве дискретных отсчетов, которые используются для анализа;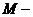 дискретно представленный частотный диапазон, в котором производится частотное представление сигналов.
дискретно представленный частотный диапазон, в котором производится частотное представление сигналов.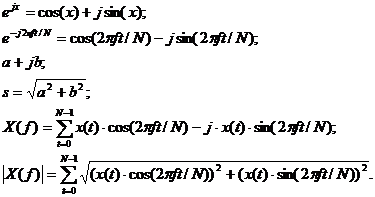

 . Термин вейвлет обозначает локализованные во временной и частотной областях функции, обладающие следующими свойствами:
. Термин вейвлет обозначает локализованные во временной и частотной областях функции, обладающие следующими свойствами: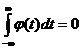 .
.
 .
.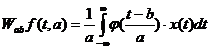 (4.1)
(4.1) ) записывается в виде (4.1). В формуле (4.1) параметр «b» меняется в интервале от
) записывается в виде (4.1). В формуле (4.1) параметр «b» меняется в интервале от  до
до  , пробегая всю временную ось, т.е. всю временную область, на которой определена функция x(t). Параметр «a» меняется от 0 до
, пробегая всю временную ось, т.е. всю временную область, на которой определена функция x(t). Параметр «a» меняется от 0 до 
 в a раз по горизонтали в 1/a раз по вертикали;
в a раз по горизонтали в 1/a раз по вертикали; по оси времени;
по оси времени;
 Вейвлет Морле
Вейвлет Морле
 (4.2)
(4.2) вейвлет;
вейвлет; длительность окна вейвлет преобразования.
длительность окна вейвлет преобразования.
 нормализующий коэффициент.
нормализующий коэффициент.





 U(T) U(T)
U(T) U(T)
 U0
U0
 (5.1)
(5.1) (5.2)
(5.2) y(n)
y(n)
 F(x'(n))
F(x'(n)) ФНЧ
ФНЧ ФВЧ
ФВЧ Полосовой фильтр
Полосовой фильтр Режекторный фильтр
Режекторный фильтр ;
;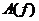 , или к характеристике ослабления
, или к характеристике ослабления  , представляют собой АЧХ, выраженных в логарифмическом масштабе. Их связь выражена:
, представляют собой АЧХ, выраженных в логарифмическом масштабе. Их связь выражена:
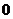 <
<  <
<  .
.



 . Ширина полосы пропускания
. Ширина полосы пропускания 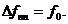
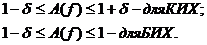
 максимально допустимое отклонение от 1.
максимально допустимое отклонение от 1. до значения верхней максимально возможной частоты
до значения верхней максимально возможной частоты  . Ширина полосы задерживания
. Ширина полосы задерживания 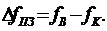 Допустимые отклонения АЧХ в полосе задерживания для КИХ-фильтров и БИХ-фильтров:
Допустимые отклонения АЧХ в полосе задерживания для КИХ-фильтров и БИХ-фильтров:
 максимально допустимое отклонение АЧХ от нуля.
максимально допустимое отклонение АЧХ от нуля. , так как в этой полосе требования не задаются, то удовлетворительным окажется любое решение, если оно соответствует требованиям в полосе пропускания и полосе задержки.
, так как в этой полосе требования не задаются, то удовлетворительным окажется любое решение, если оно соответствует требованиям в полосе пропускания и полосе задержки. . Ширина полосы задерживания
. Ширина полосы задерживания  .
.
 , ширина
, ширина  . Полоса пропускания:
. Полоса пропускания:  , ширина
, ширина 

 граничная частота ПЗ1, ширина ПЗ1
граничная частота ПЗ1, ширина ПЗ1 
 левая частота среза полосы пропускания;
левая частота среза полосы пропускания; правая частота среза ПП;
правая частота среза ПП;
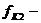 граничная частота ПЗ2;
граничная частота ПЗ2; 



 , где N – порядок фильтра
, где N – порядок фильтра

 , где k- номер рассчитываемого полюса.
, где k- номер рассчитываемого полюса.

 , где
, где  ;
; 





 , где
, где  - эллиптический полином
- эллиптический полином 



