ПАРНОЙ РЕГРЕССИИ И ВЫЧИСЛЕНИЕ ПОГРЕШНОСТИ
Цель работы. Получение навыков построения линейной модели по данным экспериментов.
Порядок выполнения.
1 Войдите в среду MATLAB 6.5 (см. лаб. работу № 1)
2 Изучите примеры и выполните задания из п.1 и п. 2.
3 Введите вектора x и y для своего варианта задания п. 3.
4 Вычислите коэффициенты системы уравнений для получения коэффициентов линейной парной регрессии.
5 Решите полученную систему уравнений.
6 Выведите на график точки корреляционного поля, полученную прямую и прямую, полученную системой MATLAB 6.5. Убедитесь, что прямые совпали, в противном случае найдите ошибку в вычислениях или исходных данных.
7 Проведите анализ достоверности модели, рассчитав коэффициент корреляции и стандартное квадратичное отклонение.
8 Сделайте вывод об адекватности полученной модели.
Нахождение суммы элементов вектора
Для нахождения суммы элементов вектора используется функция sum(<переменная-вектор>).
Например, найти 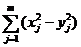 , где x, y –векторные переменные:
, где x, y –векторные переменные:
>>sum(x.*x–y.*y)
Задание. Вычислить:
1 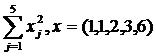 .
.
2 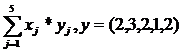 .
.
Решение систем алгебраических уравнений
В среде MATLAB можно выполнять символьные вычисления и преобразования, то есть формулировать задачу и получать решения не только в численной, но и в аналитической форме (например, символьное дифференцирование и интегрирование, упрощение математических выражений, получение решения систем уравнений в аналитической форме).
Для реализации символьных вычислений необходимо создать символьные переменные. В отличие от обычных переменных, символьным переменным не нужно присваивать никаких значений. Они получают свои значения в результате решения задачи в символьном виде. Объявляются символьные переменные следующим образом:
>> syms x y z
Для решения алгебраических уравнений и систем уравнений служит функция solve (уравнение 1, уравнение 2,…, уравнение N, переменная 1, переменная 2,…, переменная N), где переменные являются символьными переменными, относительно которых решается система уравнений.
Например, решить систему уравнений:
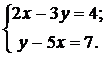
>> syms x y
>>S=solve(‘2* x –3* y =4’,’ y –5* x =7’, x,y)
Ответ будет:
S = x: [1x1 sym ]
y: [1x1 sym ]
Для получения решения в аналитической форме необходимо обратиться к S.x, S.y:
>> S.x
>> S.y
Для вычисления числовых значений с командной строки ввести полученные в аналитической форме выражения.
Задание. Получить аналитическое и численное решения системы уравнений:
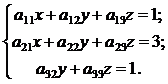
a 11=2, a 12=-1, a 13=-3, a 21=-1, a 22=4, a 23=5, a 32=-1, a 33=2
Применение метода наименьших квадратов
Для получения коэффициентов парной линейной регрессии
Краткие сведения из теории
Регрессионным анализом называется метод построения модели на основе экспериментальных данных.
Применение регрессионного анализа для обработки результатов наблюдений позволяет получить теоретическую зависимость (регрессию) переменных состояния системы от ее параметров и входных воздействий.
Совокупность точек в пространстве, соответствующих экспериментальным данным (каждая из осей соответствует входному воздействию или параметру системы, одна из осей представляет собой отклик системы), называется корреляционным полем.
Различают парную и множественную регрессию.
Регрессия называется парной, если она представляет собой зависимость переменной y от единственной переменной x.
Регрессия называется множественной, если получена зависимость переменной y от нескольких переменных x1, x2, …,xn.
Линейная регрессия ищется в виде линейной функции, нелинейная – в виде некоторой разновидности нелинейных функций.
Регрессионный анализ состоит из двух основных этапов.
1 Определяется вид зависимости (общий вид функции) y = f(x), характер поведения которой близок к описанию поведения точек корреляционного поля.
2 Определяются параметры этой функции, при которых она наилучшим образом описывает (аппроксимирует) поведение точек корреляционного поля.
Для нахождения теоретической линии регрессии (параметров выбранной функции) по данным экспериментальных замеров применяется метод наименьших квадратов.
Суть его состоит в том, что отыскивается теоретическая линия регрессии у по х, такая, что сумма квадратов расстояний от этой линии до каждой экспериментальной точки с такими же х- координатами минимальна.
То есть, функция регрессии у по х строится таким образом, чтобы соблюдался принцип наименьших квадратов:
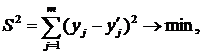 (2.1)
(2.1)
где j – порядковый номер точки в экспериментальном числовом ряду:
yj – экспериментальное значение y для определенного значения аргумента х i;
y'j – расчетное значение y при заданной величине аргумента х i в соответствии с их теоретической взаимосвязью (то есть полученное путем подстановки х i в уравнение теоретической зависимости).
Для нахождения значений параметров функции, соответствующих принципу наименьших квадратов, находятся частные производные функции по этим параметрам и приравниваются к нулю. Решая полученную систему уравнений, получаем параметры функции, при которых она максимально приближена к точкам корреляционного поля.
Линейная парная регрессия
Линейная парная регрессия ищется в виде:
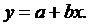 (2.2)
(2.2)
Задача сводится к отысканию коэффициентов регрессии а и b уравнения (2.2), при которых сумма квадратов отклонений точек корреляционного поля от прямой будет минимальна.
Величина D yj, представляющая собой расстояние от каждой точки корреляционного поля до теоретической линии регрессии, определяется из уравнения
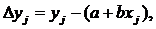 (2.3)
(2.3)
где xj– параметр х, соответствующий измеренному значению yj.
Для определения численных значений коэффициентов регрессии a и b, исходя изпринципа минимизации квадратов отклонений, нужно приравнять нулю частные производные функции S 2 уравнения (2.1) по a и b:
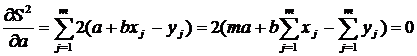 ; (2.4)
; (2.4)
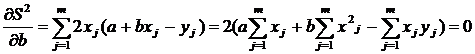 . (2.5)
. (2.5)
Выполнив необходимые преобразования уравнений (2.4), (2.5), получим систему двух уравнений с двумя неизвестными для определения a и b:
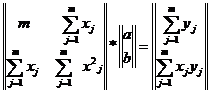 . (2.6)
. (2.6)
Решая систему уравнений (2.6) относительно a и b, находим численные значения коэффициентов регрессии.
Задание
Получить в аналитической форме и вычислить значения коэффициентов парной линейной регрессии с помощью МНК для следующих рядов данных экспериментов (первое число в скобке – входное значение x, второе – соответствующее ему значение y).
Варианты исходных данных
1 (1, 9.8); (1, 9.6); (1,10.6); (2,11.8); (2,13.0); (3,15.4); (3,13.8); (3,12.4); (4,15.4); (5,19.2); (5,18.2); (6,19.4); (6,18.6); (6,18.8); (7,22.0); (8,23.6); (9,25.4); (9,26.0); (10,26.8); (10,26.4).
2 (1, 7.8); (1, 7.0); (1, 7.6); (2,14.2); (2,13.6); (3,20.6); (3,17.4); (3,20.6); (4,25.0); (5,30.6); (5,31.4); (6,36.8); (6,38.8); (6,38.8); (7,44.0); (8,48.6); (9,54.4); (9,54.0); (10,62.4); (10,60.2).
3 (1, 6.6); (1, 6.8); (1, 7.4); (2,11.8); (2,11.8); (3,13.0); (3,14.2); (3,13.4); (4,14.8); (5,18.8); (5,20.2); (6,22.0); (6,20.4); (6,21.4); (7,26.6); (8,27.6); (9,32.8); (9,32.6); (10,35.2); (10,34.0).
4 (1,14.0); (1,12.6); (1,13.8); (2,20.8); (2,18.6); (3,22.2); (3,24.4); (3,23.8); (4,27.6); (5,32.2); (5,33.2); (6,40.0); (6,40.8); (6,40.4); (7,44.4); (8,48.6); (9,52.2); (9,52.6); (10,57.6); (10,60.0).
5 (1,19.4); (1,18.6); (1,19.6); (2,26.8); (2,27.8); (3,34.8); (3,35.8); (3,34.2); (4,41.4); (5,51.2); (5,50.4); (6,58.8); (6,58.6); (6,59.0); (7,66.6); (8,75.8); (9,81.6); (9,84.6); (10,90.4); (10,92.4).
6 (1,10.0); (1, 7.8); (1, 8.2); (2,16.6); (2,14.4); (3,21.2); (3,23.4); (3,22.2); (4,29.2); (5,36.0); (5,37.0); (6,44.2); (6,43.8); (6,45.0); (7,51.8); (8,58.6); (9,63.2); (9,63.8); (10,70.4); (10,72.0);



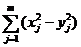 , где x, y –векторные переменные:
, где x, y –векторные переменные: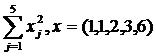 .
.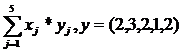 .
.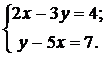
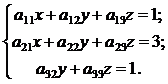
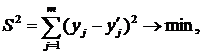 (2.1)
(2.1)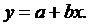 (2.2)
(2.2)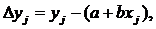 (2.3)
(2.3)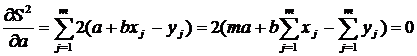 ; (2.4)
; (2.4)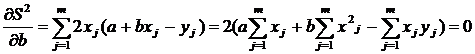 . (2.5)
. (2.5)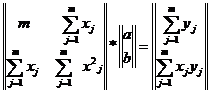 . (2.6)
. (2.6)


