
 1. Найти по обучающим выборкам векторы средних X и Y и оценки
1. Найти по обучающим выборкам векторы средних X и Y и оценки
ковариационных матриц
S ˆ x и
S ˆ y.
2. Построить «исправленную» совместную ковариационную матрицу S ˆ:
S ˆ =
 n 1 + n 2
n 1 + n 2
((n
− 2
−1) ⋅ S ˆ x
+ (n 2
−1) ⋅ S ˆ y).
3. Найти матрицу оценок коэффициентов дискриминантной функции:
a
 ⎜ 1 ⎟
⎜ 1 ⎟
 ⎛
⎛
⎜
A = ⎜
⎞
a
⎟ = S ˆ −1 ⋅(X − Y).
⎜ M ⎟
⎜ ap ⎟
⎝ ⎠
 Таким образом, получим дискриминантную функцию
Таким образом, получим дискриминантную функцию
C = a 1 x 1 + a 2 x 2 +...+ apxp.
4. Рассчитать значения дискриминантной функции для каждого объекта обоих
классов. Для этого подставить в неё элементы строк матрицы X, а затем
строк матрицы
Y – получим числа:
f 11,
f 12, …,
f 1 n и
f 21,
f 22, …,
f 2 n.
5. Найти для каждого класса среднее значение дискриминантной функции


f = 1
i
ni
∑ fij
j =1
(i =1, 2) и константу дискриминации:
С = 1 (f +
 2 1
2 1

f 2).
6. После получения константы дискриминации проверить правильность рас- пределения объектов в уже существующих классах, а также провести классификацию новых объектов: для каждой строки z матрицы Z найти
значение
f (z)
дискриминантной функции и сравнить его с константой
дискриминации C. Если
f (z) > C, то отнести новый объект к первому
классу, в противном случае – ко второму.
Пример 14.1. Имеются данные по двум группам промышленных пред-
приятий:
X 1 – фондоотдача основных производственных фондов,
X 2 – затра-
ты на тысячу рублей произведенной продукции (руб.),
X 3 – затраты сырья и
материалов на тысячу рублей произведенной продукции (руб.). Данные пред-
ставлены в таблице.
| № группы
| № предприятия
| X 1
| X 2
| X 3
|
|
I
|
| 0,49
0,65
0,67
0,59
| 94,2
75,3
85,2
98,9
| 8,49
8,76
9,20
8,45
|
|
II
|
| 1,32
1,19
1,50
| 82,5
95,4
86,1
| 4,90
6,93
4,75
|
Проведите классификацию трех новых предприятий, имеющих следую-
щие значения исходных переменных:
1-е предприятие:
2-е предприятие:
3-е предприятие:
x 1 =1,05,
x 1 = 0,7,
x 1 =1,3,
x 2 =90,
x 2 = 70,
x 2 = 85,
x 3 =5,2;
x 3 = 9,8;
x 3 = 4,2.
Решение. Запишем значения исходных данных для каждой группы предприятий в виде матриц:
⎛ 0,49
⎜
X = ⎜0,65
⎜0,67
⎜
⎝0,59
94,2
75,3
85,2
98,9
8,49⎞
⎟
8,76⎟
9,20⎟,
⎟
8,45⎠
⎛1,32
⎜
Y = ⎜1,19
⎜1,50
82,5
95,4
86,1
4,90 ⎞
⎟
6,93 ⎟,
4,75⎟
⎛1,05 90
⎜
Z = ⎜ 0,7 70
⎜ 1,3 85
5,2 ⎞
⎟
9,8 ⎟.
4,2 ⎟
Рассчитаем средние значения каждой переменной в каждой группе – оп-
ределим центры этих групп:
⎛ 0,6 ⎞
⎛1,34 ⎞

 ⎜ ⎟ ⎜ ⎟
⎜ ⎟ ⎜ ⎟
X = ⎜88,4 ⎟,
Y = ⎜
88 ⎟
⎜ ⎟ ⎜ ⎟
⎝8,73 ⎠
⎝5,53⎠
и оценки ковариационных матриц
S ˆ x и
S ˆ y:
⎛ 0,01
⎜
− 0,54
0,02 ⎞
⎟
⎛ 0,02
⎜
− 0,65
− 0,16⎞
⎟
S ˆ x = ⎜− 0,54
⎜
108,58
− 2,08⎟,
⎟
S ˆ y = ⎜− 0,65
⎜
44,31
7,65 ⎟.
⎟
⎝ 0,02
− 2,08
0,12 ⎠
⎝− 0,16
7,65
1,48 ⎠
Тогда «исправленная» совместная ковариационная матрица
⎛ 0,01
⎜
− 0,59
− 0,05 ⎞
⎟
S ˆ =
 4 + 3 − 2
4 + 3 − 2
((4 −1) ⋅ S ˆ
+ (3 −1) ⋅ S ˆ y
)= ⎜− 0,59
⎝− 0,05
82,87
1,82
1,82 ⎟.
0,66 ⎟
Обратная матрица по отношению к S ˆ:
⎛141,68
⎜
0,81
8,82 ⎞
⎟
S ˆ −1 = ⎜
⎜
⎝
0,81
8,82
0,02
0,02
0,02 ⎟.
2,15 ⎟
Найдем матрицу оценок коэффициентов дискриминантной функции:
⎛141,68
0,81
8,82 ⎞
⎛− 0,74 ⎞
⎛− 75,83⎞
⎜ ⎟ ⎜ ⎟ ⎜ ⎟

 A = S ˆ −1 ⋅(X − Y) = ⎜
A = S ˆ −1 ⋅(X − Y) = ⎜
0,81
0,02
0,02 ⎟⋅⎜
0,4
⎟ = ⎜ − 0,54 ⎟.
⎜ 8,82
0,02
2,15 ⎟ ⎜
3,2 ⎟
⎜ 0,38 ⎟
Таким образом, получим дискриминантную функцию
C = −75,83 x 1 −0,54 x 2 +0,38 x 3.
77
Вычислим значения дискриминантной функции для каждого предпри-
ятия двух групп. Для первой группы получим:
f 11 = −84,68,
f 12 = −86,52,
f 13 = −93,21,
f 14 = −94,81; среднее значение
f 1 = −89,81. Для второй группы:
 f 21 = −142,69,
f 21 = −142,69,
f 22 = −139,01,
f 13 = −158,34; среднее значение
f 2 = −146,68.
Константа дискриминации:
С = 1 (−89,81−146,68) = −118,24.
 2
2
Проведём теперь классификацию новых предприятий: для каждой стро-
 ки z матрицы Z найдем значение
ки z матрицы Z найдем значение
f (z)
дискриминантной функции:
f 1 = −126,14 < C,
f 2 = −87,6 > C,
f 3 = −142,79 < C.
Итак, согласно методу дискриминантного анализа первое и третье новые предприятия нужно отнести ко второй группе, а второе – к первой группе.
В случае, когда число классов больше двух, решение задачи дискрими- нантного анализа усложняется. В такой ситуации можно применить следую- щие две процедуры.
1. Выбрать произвольную пару классов и выяснить, пользуясь предыду- щими рассуждениями, к какому из этих классов классифицируемый объект не принадлежит. Этот класс отбросить. Из оставшихся классов выбрать лю-
бые два и повторить рассуждения. Продолжить это процесс, каждый раз уменьшая число классов на один, до завершения.
2. Можно также указать процедуру, не зависящую от порядка рассмот-
рения пар классов: рассмотреть все пары классов и запомнить на каждом ша- ге номер класса, к которому причисляется классифицируемый объект. Отне- сти его к классу, который встречается чаще всего.
Теоретические вопросы и задания
1. В чем состоит сущность дискриминантного анализа?
2. Сформулируйте правило дискриминации (алгоритм дискриминантного анализа).
3. Как определяется минимальное число дискриминантных функций?
Задачи и упражнения
1. В таблице приведены группы фермерских хозяйств с высоким и низким уровнями организации управления производством, а также хозяйства, под- лежащие классификации.
|
Хозяйства
| Производительность труда X 1
(млн руб. / чел.)
|
Рентабельность X 2 (%)
|
|
Высокого уровня
| 9,1
6,6
5,2
| 23,4
19,1
17,5
|
|
Низкого уровня
| 4,1
5,1
6,2
6,6
| 5,4
6,6
8,0
9,7
|
|
Подлежащие классификации
| 7,4
9,4
6,5
| 10,0
12,1
12,7
|
С помощью дискриминантного анализа классифицируйте указанные три хозяйства.
2. По эффективности работы выделены две группы, состоящие из четырех и
пяти однотипных фирм. Для этих групп по показателям:
X 1 – стоимость
реализованной продукции (млн руб.),
X 2 – брак выпущенной продукции
(%), – были получены векторы средних:

 ⎛6,72 ⎞
⎛6,72 ⎞
⎛4,2 ⎞
X = ⎜ ⎟,
9,34
Y = ⎜ ⎟
 2,5
2,5
⎝ ⎠ ⎝ ⎠
и ковариационные матрицы:

S = 1 ⎛1,07
⎝
0,23⎞
⎟,
0,08 ⎠
1 ⎛0,30
Sy ⎜
5 ⎝0,16
0,16 ⎞
⎟.
0,24 ⎠
К какой из групп следует отнести фирму с показателями
x 1 =5,46;
x 2 =3?
3. Решите задачу из примера 14.1 в случае, когда имеется еще одна группа предприятий.
|
Группа
| Номер
предприятия
|
X
|
X
|
X
| |
III
|
| 1,52
1,20
1,46
| 81,5
93,8
86,5
| 4,95
6,95
8,45
|
| |
1 2 3
Домашнее задание
1. Имеется два множества объектов. Обучающие выборки записаны в табли-
це (a – число букв в фамилии, b – число букв в имени).
| Множество
| X 1
| X 2
| X 3
|
|
I
| 5+0,1 a
6+0,1 a
7+0,1 a
| 50+0,5 b
40+0,5 b
60+0,5 b
| 2+0,1 b
1+0,1 b
3+0,1 b
|
|
II
| 2+0,1 a
4+0,1 a
5+0,1 a
| 60+0,5 b
30+0,5 b
70+0,5 b
| 3+0,1 b
4+0,1 b
2+0,1 b
|
С помощью дискриминантного анализа выясните, к какому из множеств
следует отнести объект с показателями:
x 1 = 2,5;
x 2 = 75;
x 3 = 4,5.
Занятие 15. Классификация без обучения.
Кластерный анализ
Одним из важнейших направлений статистических исследований явля-
ется кластерный анализ.
Определение 15.1. Кластерный анализ – совокупность методов объединения объектов, характеризующихся несколькими признаками, в груп- пы, кластеры (от англ. cluster – сгущение, пучок).
Методы кластерного анализа позволяют выявить структуру между объ- ектами наблюдаемой совокупности. Кроме того, они могут быть использова- ны с целью сжатия информации, что также важно при статистических иссле- дованиях.
Все методы кластерного анализа можно разделить на две группы:
иерархические и итеративные.
В свою очередь, иерархические методы можно разделить на
агломеративные (от англ. agglomerate – собирать) и дивизивные (от англ. division – разделять). Агломеративные методы последовательно объединяют
отдельные объекты в кластеры, а дивизивные – расщепляют кластеры на отдельные группы.
К итеративным методам относятся метод k -средних, метод поиска сгу-
щений и т.д. Особенность этих методов состоит в том, что кластеры форми- руются исходя из заданных условий разбиения (параметров), например числа кластеров.
Основой кластерного анализа является понятие «близости» объектов,
«расстояния» между объектами. В зависимости от решаемой задачи рас- стояние между объектами определяется по-разному. Часто используются следующие расстояния:
1) евклидово расстояние:
ρ ij =
p
∑ (
xik
 k =1
k =1
− xjk);

p
2) взвешенное евклидово расстояние:
ρ ij =
∑ω k (xik
− xjk)
, которое
k =1
применяется в случае, когда каждая компонента имеет некоторый
«вес»
ω k, пропорциональный степени важности соответствующего
p
признака (обычно
0 ≤ ω k ≤1, ∑ω k
k =1
=1);
3) расстояние Махаланобиса21:
ρ ij =

(
Xi
− Xj
) T ⋅ S ˆ−1 ⋅(X
− Xj
), где
X i,
Xj – векторы значений i -го и j -го объектов, S ˆ – общая ковариацион-
21 Прасанта Чандра Махаланобис (1893 – 1972) – индийский экономист и статистик.
 80
80
ная матрица (если переменные некоррелированы, то расстояние Маха-
ланобиса совпадает с обычным евклидовым расстоянием);
4) расстояние Хемминга22 – число различных компонент векторов
Xi и
Xj (особенно часто расстояние Хемминга применяется, когда призна-
ки измеряются в номинальных шкалах).
Также важно определить расстояние между кластерами. Наиболее употребительны следующие расстояния между классами:
1) по принципу «ближайшего соседа» (одиночной связи) – наименьшее из расстояний между объектами различных кластеров;
2) по принципу «дальнего соседа» (полной связи) – наибольшее из рас-
стояний между объектами различных кластеров;
3) по принципу средней связи – среднее арифметическое всех попарных расстояний между объектами различных кластеров.
Замечание. Если известны расстояния между любыми двумя из трёх
кластеров
Sl,
Sm и
Sq, то для нахождения расстояния между кластером Sl и
кластером
Sm, q, который получается объединением
Sm и
Sq, удобно пользо-
ваться формулой:
где
ρ l (m, q) = a ⋅ ρ lm + b ⋅ ρ lq + c | ρ lm − ρ lq |,
 для принципа «ближайшего соседа»:
для принципа «ближайшего соседа»:
a = b = − c = 1;
для принципа «дальнего соседа»:
a = b = c = 1;
 2
2
для принципа средней связи:
a = nm
 nm + nq
nm + nq
, b =
nq,
 nm + nq
nm + nq
c = 0
(nm, nq
– количество объектов в классах
Sm и Sq
соответственно).
Замечание. Выбирая различные способы определения расстояния ме- жду объектами и кластерами, получают, вообще говоря, различные класси- фикации. Для определения качества разбиения на кластеры используют, как правило, один из следующих функционалов качества классификации:
 k
k
1) Q 1
= ∑ ∑ ρ2 (x, x)
i =1 x ∈ Si
– сумма внутриклассовых сумм квадратов отклоне-
ний (здесь Sj
(j =1, 2,..., k) – кластеры, которые получены в результа-
те разбиения);
k

2)
Q = σ 2
i
– сумма внутриклассовых дисперсий;
i =1
22 Ричард Уэсли Хемминг (1915- – 1998) – американский математик.
⎛ k ⎞
3) Q 3 = det⎜∑ ni ⋅cov Si ⎟.
⎝ i =1 ⎠
Приведем пример агломеративного иерархического метода.
Пример 15.1. По иерархическому алгоритму проведите классификацию
n = 6
предприятий машиностроения, деятельность которых характеризуется
показателями
X 1 – рентабельность (%),
X 2 – производительность труда.
| №
|
|
|
|
|
|
|
| X 1
| 23,4
| 17,5
| 9,7
| 18,2
| 6,6
| 8,0
|
| X 2
| 9,1
| 5,2
| 5,5
| 9,4
| 7,5
| 5,7
|
Решение. Найдем расстояния между объектами, используя обычное евклидово расстояние, например:
 ρ12 =
ρ12 =
(23,4 − 17,5)2 + (9,1 − 5,2)2
≈ 7,07.
В результате получим матрицу расстояний:
⎛ 0 7,07
⎜
14,16
5,21
16,88
15,77⎞
⎟
⎜ 7,07
⎜14,16
ρ1 = ⎜
⎜ 5,21
⎜16,88
⎜
7,81
4,26
11,14
7,81
9,35
3,69
4,26
9,35
11,75
11,14
3,69
11,75
9,51 ⎟
1,71 ⎟
⎟.
10,85⎟
2,28 ⎟
⎟
⎝15,77
9,51
1,71
10,85
2,28 0 ⎠
Из матрицы расстояний видно, что самые близкие объекты – 3 и 6, и по-
этому объединяем их в один кластер. Получим пять кластеров:
| № кластера
|
|
|
|
|
|
| Состав
| (1)
| (2)
| (3; 6)
| (4)
| (5)
|
Расстояние между кластерами будем искать по принципу «ближайшего соседа». Так, например,


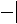
 ρ = 1 ρ
ρ = 1 ρ
+ 1 ρ
− 1 ρ − ρ
=14,16.
(1),(3;6)
2 13
2 16
2 13 16
Получим матрицу расстояний:
⎜
| ⎛ 0
| 7,07
| 14,16
| 5,21
| 16,88 ⎞
⎟
11,14 ⎟
3,69 ⎟
⎟
| | ⎜ 7,07
|
| 7,81
| 4,26
| | ⎜14,16
⎜
| 7,81
|
| 9,35
| | ⎜ 5,21
| 4,26
| 9,35
|
| 11,75 ⎟
| | ⎜
⎝16,88
| 11,14
| 3,69
| 11,75
| 0 ⎟
⎠
|
| |
ρ2 =.
Объединим кластеры 3 и 5 в один кластер, получим четыре кластера:
| № кластера
|
|
|
|
|
| Состав
| (1)
| (2)
| (3; 5; 6)
| (4)
|
Матрица расстояний
⎛ 0 7,07
⎜
14,16
5,21⎞
⎟
ρ =⎜ 7,07
3 ⎜14,16
⎜
7,81
7,81
4,26⎟
9,35⎟.
⎟
⎝ 5,21
4,26
9,35 0 ⎠
Далее объединим кластеры 2 и 4:
| № кластера
|
|
|
|
| Состав
| (1)
| (2; 4)
| (3; 5; 6)
|
Матрица расстояний
⎛ 0 7,07
⎜
14,16 ⎞
⎟
ρ4 = ⎜ 7,07 0
| № кластера
|
|
| | Состав
| (1; 2; 4)
| (3; 5; 6)
|
| |
⎜
7,81 ⎟.
⎟
⎝14,16
Объединим кластеры 1 и 2:
7,81 0 ⎠
Матрица расстояний
⎛ 0 7,81⎞
ρ5 =⎜ ⎟.
⎝7,81 0 ⎠
Графически описанный процесс представляют в виде дендрограммы
(рис. 15.1).

Рис. 15.1
Пример 15.2. По данной матрице расстояний между объектами прове-
дите классификацию с помощью дивизивного иерархического метода:
⎜
⎜4,49
ρ= ⎜ 2,16
⎜
⎜3,53
⎜
3,26
1,92
3,26
2,68
1,92
2,68
⎟
1,93⎟
2,74⎟.
⎟
0,71⎟
⎟
⎝3,24
1,93
2,74
0,71 0 ⎠
Решение. Наиболее удаленными являются объекты 1 и 2. Оценим рас-
стояния от других объектов до объектов 1 и 2: объект 3 ближе к объекту 1, чем к 2, а объекты 4 и 5 ближе к 2, чем к 1. Таким образом, получили два кластера: (1; 3) и (2; 4; 5).
В каждом из этих кластеров анализируем расстояния между объектами и разделяем тот кластер, в котором расстояние между объектами наибольшее:
ρ13 = 2,16;
ρ24 =1,92;
ρ25 =1,93;
ρ45 = 0,71. Следовательно, объекты 1 и 3
выделяем в отдельные кластеры.
Аналогично на следующем шаге кластер (2; 4; 5) разделяем на два: (2) и
(4; 5). Наконец на последнем шаге разделяем кластер (4; 5) на два кластера.
Описанный алгоритм удобно графически представить в виде следующе-
го графа (рис. 15.2).

Рис. 15.2
Рассмотрим теперь один из итеративных методов – метод k -средних,
особенность которого состоит в заданном количестве кластеров.
Пусть имеется n объектов, которые нужно разбить на k кластеров.
Алгоритм метода k - средних
1. Выбрать из имеющихся n объектов произвольным образом k, которые назовём эталонами. Присвоить каждому из k эталонов единичный вес. Таким образом, получим k кластеров, в каждом из которых находится по одному объекту.
2. Из оставшихся объектов выбрать произвольным образом один, опреде- лить, к какому из имеющихся эталонов он ближе всего (согласно выбран- ному расстоянию), и поместить его в соответствующий кластер. Найден- ный эталон заменить «усредненным объектом» и его вес увеличить на
единицу. Повторить эту процедуру
n − k
раз, т.е. до тех пор, пока все объ-
екты не окажутся принадлежащими одному из k кластеров.
3. Для проверки качества разбиения все n объектов присоединить к полу- ченным кластерам, «усредняя» эталон и накапливая вес. Если новое раз- биение совпадёт с полученным в предыдущем пункте, то классификацию завершить. В противном случае – повторить п.3.
Пример 15.1. Разбейте шесть объектов на три кластера при помощи ме-
тода k -средних. Каждый объект описывается тремя показателями
X 1,
X 2,
X 3.
|
|
|
|
|
|
|
|
| X 1
| 0,1
| 0,8
| 0,4
| 0,18
| 0,25
| 0,67
|
| X 2
|
|
|
|
|
|
|
| X 3
|
|
|
|
| 3,2
| 2,4
|
Решение. В качестве эталонов возьмём первые три объекта:
Y 0 = (0,1; 10, 5), Y 0 = (0,8; 14, 2), Y 0 = (0,4; 12, 3), их веса
p 0 =
p 0 =
p 0 =1.
1 2 3
1 2 3
Найдём расстояния (евклидово) от объекта 4 до каждого эталона:
ρ41 =1,42;
ρ42 = 3,68;
ρ43 =1,43.
Следовательно, объект 4 должен быть отнесён к первому эталону, и он пере-
считывается:
0 0
Y 1 =
p 1 Y 1
+ Y 4
= (0,14; 10,5; 4,5),
p 1 = 2,

1
p 0 +1 1
а остальные эталоны остаются без изменений: Y 1 = Y 0, Y 1 = Y 0,
p 1 = p 1 =1.
2 2 3 3 2 3
Аналогично находим расстояния от объекта 5 до каждого эталона. Он ближе всего к третьему эталону, поэтому присоединяем объект 5 к нему и пересчитаем эталон:
1 1
Y 2 =
p 3 Y 3
+ Y 5
= (0,33; 12,5; 3,1),
p 2 = 2,

3
p 1 +1 3
аостальные эталоны остаются без изменений: Y 2 = Y 1, Y 2 = Y 1,
p 2 = 2,
p 2 =1.
1 1 2 2 1 2
Так же получаем, что объект 6 нужно присоединить ко второму эталону, и пересчитываем его. Таким образом, имеем следующие кластеры: (1; 4), (2; 6), (3; 5), каждый из которых характеризуется своим эталоном и весом.
Теперь проведём пересмотр разбиения на кластеры. Для этого каждый из шести объектов присоединим к соответствующему эталону.
Объект 1 оказывается ближе всего к первому эталону, поэтому его при-
соединяем к этому эталону и пересчитываем. Аналогично поступаем со все-
ми остальными объектами. В результате получим такое же разбиение, как и
вначале. Имеющаяся устойчивость показывает, что алгоритм можно заканчи-
вать.
 Для выяснения качества разбиения найдём сумму внутриклассовых дис-
Для выяснения качества разбиения найдём сумму внутриклассовых дис-
k

персий
Q = σ 2.
i
i =1
 Для первого класса находим средние
Для первого класса находим средние
x 11 = 0,14;
x 12 =10,5;
x 13 = 4,5 и
2
дисперсии
σ11 = 0,0016; σ12 = 0,25; σ11 = 0,25. Таким образом, σ S
= 0,5.
Аналогично, σ2
= 0,27; σ2


3
= 0,32. Значит, Q 2
=1,09.
Заметим, что при иерархическом способе построения кластеров с расстоянием по принципу «дальнего соседа» получили бы следующее разбиение на три класса: (1), (2; 6), (3; 4; 5), и внутриклассовая дисперсия
такого разбиения
Q 2 =1,16. Следовательно, разбиение, полученное методом
k -средних, более качественное.
Теоретические вопросы и задания
 1. В чем суть задачи кластерного анализа? Что является основой для прове-
1. В чем суть задачи кластерного анализа? Что является основой для прове-
дения кластерного анализа?
2. Какие способы определения «близости» объектов и кластеров Вы знаете?
3. Какие существуют иерархические методы кластерного анализа? Каков ал-
горитм этих методов?
4. Сформулируйте алгоритм метода k -средних.
5. Как можно сравнить два различных разбиения на кластеры?
Задачи и упражнения
1. Проведите классификацию шести предприятий, данные о которых приве- дены в первом примере, измеряя расстояние между кластерами по принци- пу «дальнего соседа». Сравните полученные два разбиения с помощью функционала внутриклассовых дисперсий.
2. Используя метод k -средних, разбейте на два кластера 5 объектов:
Домашнее задание
1. По агломеративному алгоритму проведите классификацию шести регионов по уровню медицинского обслуживания населения, который характеризует-
ся показателями:
10 тыс. жителей.
X 1 – число врачей,
X 2 – число больничных коек на
| №
|
|
|
|
|
|
|
| X 1
| 34,8
| 31,2
| 32,1
| 35,7
| 30,2
| 34,2
|
| X 2
|
|
|
|
|
|
|
Указание. За расстояние между объектами примите взвешенное евклидово
расстояние: ω1 = 0,4; ω2 = 0,6, а расстояние между кластерами определите
по принципу «дальнего соседа».
2. Используя метод k -средних, классифицируйте регионы из задачи 1 на два кластера. Сравните полученные два разбиения с помощью функционала внутриклассовых дисперсий.
Занятие 16. Канонические корреляции.




 1. Найти по обучающим выборкам векторы средних X и Y и оценки
1. Найти по обучающим выборкам векторы средних X и Y и оценки n 1 + n 2
n 1 + n 2 ⎛
⎛ Таким образом, получим дискриминантную функцию
Таким образом, получим дискриминантную функцию

 2 1
2 1
 ⎜ ⎟ ⎜ ⎟
⎜ ⎟ ⎜ ⎟ 4 + 3 − 2
4 + 3 − 2 f 21 = −142,69,
f 21 = −142,69, ки z матрицы Z найдем значение
ки z матрицы Z найдем значение k =1
k =1

 80
80 2
2 nm + nq
nm + nq nm + nq
nm + nq k
k ρ12 =
ρ12 =

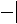
 ρ = 1 ρ
ρ = 1 ρ



 Для выяснения качества разбиения найдём сумму внутриклассовых дис-
Для выяснения качества разбиения найдём сумму внутриклассовых дис-
 Для первого класса находим средние
Для первого класса находим средние

 1. В чем суть задачи кластерного анализа? Что является основой для прове-
1. В чем суть задачи кластерного анализа? Что является основой для прове-

