Линейные блочные коды позволяют выполнять операции кодирования/декодирования не обращаясь к кодовой таблице, а используя лишь некий набор свойств, присущий всем комбинациям в кодовой таблице.(это снижает трудоемкость процесса). Любой линейный блочный код обозначается как (n,k)-код, где: k - количество информационных символов; n – длинна информационных + проверочных. для корректирующего кода n > k, и разность r = n - k есть число проверочных символов. Значения этих символов вычисляется по информационным символам с использованием ряда линейных операций.
для самого простого кода r =1 - код называется кодом с проверкой на чётность (n, n -1). Проверочный символ получается путем суммирования элементов входной комбинации  , по mod2. При декодировании достаточно провести проверку на чётность
, по mod2. При декодировании достаточно провести проверку на чётность
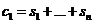 . .
| (3.9)
|
Если проверка прошла ( 0), то это означает, что такая комбинация могла быть передана. Если же проверка не прошла (
0), то это означает, что такая комбинация могла быть передана. Если же проверка не прошла ( 1), то в принятой комбинации, несомненно, есть ошибки.
1), то в принятой комбинации, несомненно, есть ошибки.
Кодовое расстояние для кода с проверкой на чётность равно двум, поэтому он обнаруживает любую однократную ошибку. Так же способен обнаружить любую ошибку нечётной кратности, но исправлять ошибки он не может.
Операции (3.8) и (3.9) – чрезвычайно простые. Для реализации каждой из них достаточно иметь один счётный триггер. Тогда сразу возникает идея для повышения корректирующей способности кода использовать не одну, а несколько проверок на чётность. При этом очевидно, что в каждой проверке участвуют не все n символов, а лишь их часть. А в разных проверках должны участвовать разные группы символов.
В качестве примера рассмотрим код (5,2). Зададим его в систематической форме, то есть первые k символов выходной комбинации должны повторять входные информационные символы, а на оставшихся r = n - k =3 позициях размещаются проверочные символы, которые предстоит вычислить при кодировании, то есть
где a – вектор-строка информационных символов, b – вектор-строка проверочных символов. В частности, рассмотренный выше простой код с проверкой на чётность тоже является систематическим.
Итак, для кода (5,2) из  всевозможных пятиразрядных комбинаций в кодовую таблицу включим лишь такие комбинации, которые удовлетворяют всем трём заданным проверкам на чётность (количество проверок на чётность всегда равно r). Результаты проведения этих r проверок для конкретной комбинации представим в виде вектора-строки
всевозможных пятиразрядных комбинаций в кодовую таблицу включим лишь такие комбинации, которые удовлетворяют всем трём заданным проверкам на чётность (количество проверок на чётность всегда равно r). Результаты проведения этих r проверок для конкретной комбинации представим в виде вектора-строки  который имеет медицинское название “синдром”, то есть, сочетание признаков, характеризующих определённое состояние. Допустим, для нашего кода мы выбрали следующую систему проверок
который имеет медицинское название “синдром”, то есть, сочетание признаков, характеризующих определённое состояние. Допустим, для нашего кода мы выбрали следующую систему проверок
 , ,
| (3.11)
|
то есть, в первой проверке участвуют символы, стоящие на первой и третьей позициях, и т.д. В кодовую таблицу (типа табл. 3.1) включим лишь те комбинации, для которых вектор c = 0.
Оказывается, что их всего 4, как и следовало ожидать (3.7).
 По приведённой таблице (табл. 3.2) легко найти, что
По приведённой таблице (табл. 3.2) легко найти, что  , то есть заданная нами система проверок на чётность (3.11) действительно однозначно определяет систематический корректирующий код, способный не только обнаружить любые однократные и двукратные ошибки, но даже исправлять все однократные ошибки.
, то есть заданная нами система проверок на чётность (3.11) действительно однозначно определяет систематический корректирующий код, способный не только обнаружить любые однократные и двукратные ошибки, но даже исправлять все однократные ошибки.
Систему проверок (3.11) можно более наглядно представить в виде рис.3.1.
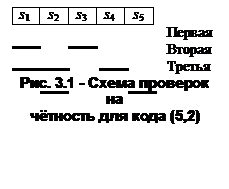 Первый этап декодирования – обнаружение ошибок – фактически сводится к проведению r проверок на чётность (3.11) в принятой кодовой комбинации. Считается, что ошибок нет, если c = 0.
Первый этап декодирования – обнаружение ошибок – фактически сводится к проведению r проверок на чётность (3.11) в принятой кодовой комбинации. Считается, что ошибок нет, если c = 0.
Если c ≠ 0, второй этап – исправление ошибок – также можно провести, пользуясь схемой рис.3.1 и рассматривая различные варианты. Например, если принята комбинация y =11110, то находим c =011 и делаем вывод о наличии ошибок в принятой комбинации. Исходя из возможностей данного кода ( ), делаем предположение, что произошла однократная ошибка (гарантированно исправлять ошибки более высоких кратностей этот код все равно не может (3.6)). Рассматривая разные варианты расположения этой одиночной ошибки, видим, что наблюдаемый результат c =011 мог быть получен лишь в случае, когда эта ошибка расположена во втором символе, следовательно, х =10110 и a =10.
), делаем предположение, что произошла однократная ошибка (гарантированно исправлять ошибки более высоких кратностей этот код все равно не может (3.6)). Рассматривая разные варианты расположения этой одиночной ошибки, видим, что наблюдаемый результат c =011 мог быть получен лишь в случае, когда эта ошибка расположена во втором символе, следовательно, х =10110 и a =10.
 Чтобы не перебирать различные варианты каждый раз при декодировании очередной кодовой комбинации, полезно заранее заготовить таблицу, в которой перечислить все возможные векторы исправляемых ошибок (однократных в нашем примере) и соответствующие им значения вектора-синдрома (табл. 3.3). Если бы код был способен исправлять ещё и все двукратные ошибки, в эту таблицу следовало бы включить дополнительно
Чтобы не перебирать различные варианты каждый раз при декодировании очередной кодовой комбинации, полезно заранее заготовить таблицу, в которой перечислить все возможные векторы исправляемых ошибок (однократных в нашем примере) и соответствующие им значения вектора-синдрома (табл. 3.3). Если бы код был способен исправлять ещё и все двукратные ошибки, в эту таблицу следовало бы включить дополнительно  векторов таких ошибок, в частности 11000, 10100 и т.д.
векторов таких ошибок, в частности 11000, 10100 и т.д.
Из табл. 3.3 видно, что анализируемый код (5,2) действительно способен исправить любую однократную ошибку, поскольку все значения c различны, а каждому c соответствует единственный вектор ошибки e. Легко убедиться, что для двукратных ошибок такого однозначного соответствия уже не будет.
Чтобы завершить обсуждение тех вычислений, которые нужно проводить при кодировании и декодировании линейных блочных кодов, полезно продолжить их формализацию, в частности, ввести для них более компактную форму записи.
Вместо схемы рис. 3.1 удобно использовать проверочную матрицу H, содержащую r строк и n столбцов и состоящую из 0 и 1. Каждая строка соответствует одной проверке на четность, причем положение единиц в этой строке указывает на позиции символов кодовой комбинации, участвующих в данной проверке. Для рассмотренного кода (5,2) такая матрица имеет вид

|
(3.12)
|
Если линейный блочный код к тому же является систематическим, матрицу H можно условно разделить на два блока H =(Q,Ir), причем левый блок имеет размеры (r  k), а правый блок - это единичная матрица (r
k), а правый блок - это единичная матрица (r  r). Для нашего примера
r). Для нашего примера
Q=  , , 
|
(3.13)
|
Операция вычисления синдрома (3.11) имеет следующий вид

| (3.14)
|
где  - транспонированная матрица H.
- транспонированная матрица H.
Кодер систематического кода заполняет первые k позиций информационными символами, поступившими на его вход. На оставшиеся r позиций он ставит проверочные символы, при этом вычисляет их значения так, чтобы для n -разрядной выходной комбинации оказалось c = 0. Для рассмотренного примера 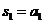 ,
,  , а из соотношений (3.11) находим три проверочных символа, завершая кодирование:
, а из соотношений (3.11) находим три проверочных символа, завершая кодирование:
Первый этап декодирования принятой n -разрядной комбинации y – это обнаружение ошибок, и он также определяется соотношением (3.14)

| (3.16)
|
Напомним, что в соответствии с (3.2) вектор ошибок e позволяет выразить принятую комбинацию y через переданную s, то есть y = s + e. Подставим эту сумму в (3.16) и напомним, что для любой передаваемой комбинации  . В итоге получим
. В итоге получим
 , ,
| (3.17)
|
то есть, синдром, вычисленный по принятой комбинации, не зависит от того, какая комбинация из кодовой таблицы была передана, а определяется лишь вектором ошибок. Именно по этой причине при обсуждении операций декодирования у нас не возникло потребности обращаться к кодовой таблице, а ограничились лишь анализом предполагаемого характера возникающих ошибок. Нетрудно догадаться, что и табл. 3.3. была составлена с использованием формулы (3.17), то есть 
Не нужно строить код так, чтобы результат какой-либо проверки на чётность следовал из остальных проверок – это пустая трата ресурсов. Кроме того, любой из n символов комбинации должен участвовать хотя бы в одной проверке. При выполнении этих условий любой матрице H соответствует единственная матрица G размера  , называемая производящей (генераторной) матрицей данного кода. Обе матрицы связаны уравнением
, называемая производящей (генераторной) матрицей данного кода. Обе матрицы связаны уравнением

| (3.18)
|
где 0 – нулевая матрица размера (k´r).
Если задана матрица H, то, решив уравнение (3.18), можно найти матрицу G. Процедура решения оказывается простой, если код является систематическим. Тогда и матрицу G условно можно разбить на два блока  , где Ik - единичная матрица
, где Ik - единичная матрица  . Используя блочные представления обеих матриц, имеем
. Используя блочные представления обеих матриц, имеем

|
(3.19)
|
то есть построенная таким образом матрица G удовлетворяет уравнению (3.18). В частности, для (5,2)-кода (3.11) матрица G имеет вид
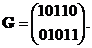
|
(3.20)
|
Из сказанного ясно, что матрица G, как и матрица H, полностью определяет код. Поэтому другая интерпретация тех же процессов кодирования и декодирования может быть основана на матрице G.
Кодирование линейным блочным кодом можно проводить по формуле
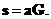
| (3.21)
|
Используя определение (3.18), видим, что синдром для полученной таким образом кодовой комбинации всегда равен нулю

| (3.22)
|
то есть эта комбинация входит в кодовую таблицу.
Возможность декодирования (вычисления синдрома) принятой комбинации с использованием матрицы G становится вполне очевидной, если код является систематическим (3.10). Из принятой комбинации  берут вектор-строку информационных символов ап и по ней заново проводят кодирование, например, по формуле (3.21), получая новое значение вектора-строки проверочных символов
берут вектор-строку информационных символов ап и по ней заново проводят кодирование, например, по формуле (3.21), получая новое значение вектора-строки проверочных символов 

| (3.23)
|
По определению (3.16), вектор-синдром для принятой комбинации s п равен

|
(3.24)
|
то есть для вычисления синдрома достаточно сложить два вектора проверочных символов: принятый и вновь вычисленный.
В заключение сделаем несколько замечаний.
1) Любой линейный блочный код обладает следующим свойством: если из кодовой таблицы взять две (или более) комбинаций и сложить их (разумеется, по модулю 2), то получим комбинацию, принадлежащую той же таблице.
2) Операцию умножения вектора-строки на матрицу удобно провести следующим образом: элементы этого вектора записываем против строк матрицы, а затем суммируем те строки, против которых оказались единицы.
3) По определению (3.4) кодовое расстояние нужно находить по кодовой таблице. Для линейных блочных кодов существует менее трудоёмкий способ: к матрице G нужно дописать строку, состоящую из нулей, и тем же способом (3.4) определить минимальное расстояние для полученной таблицы.
4) Одновременная одинаковая перестановка столбцов матриц G и H даёт новый код, эквивалентный исходному, поскольку это приводит к аналогичной перестановке соответствующих символов во всех кодовых комбинациях. Тот же результат будет, если один из двух столбцов заменить их суммой. Многократное повторение подобных операций можно применить, например, для приведения кода к систематической форме.
5) Применяются два способа реализации кодера и декодера: программный (при использовании компьютера) и аппаратный. При аппаратной реализации кодирования для любого линейного блочного кода можно применить такой универсальный (следовательно, не самый экономный) способ: входную k - разрядную последовательность информационных символов последовательно, символ за символом, ввести в k – разрядный входной регистр сдвига, чтобы иметь возможность проводить одновременно операции со всеми символами; при помощи набора сумматоров по модулю 2 вычислить раздельно все n символов кодовой комбинации по формуле (3.21) с учётом примечания 2 (для систематического кода можно ограничиться вычислением лишь проверочных символов по формулам типа (3.15)); при помощи n -входового мультиплексора вывести последовательно все n символов в нужном порядке (разумеется, и для вывода символов можно применить n -разрядный регистр сдвига, предварительно записав в него n вычисленных символов кодовой комбинации).
Универсальный способ декодирования предполагает следующие действия: n принимаемых символов последовательно вводятся в n -разрядный регистр сдвига; при помощи набора сумматоров по модулю 2 вычисляют все r элементов синдрома по формулам типа (3.11) (можно подсчитать потребное количество сумматоров даже с учётом дублирования некоторых операций); при помощи логического устройства (назовём его анализатором синдрома), пользуясь таблицей (e – c), по вычисленному значению c находят e, то есть номера ошибочных символов; при помощи k -входового мультиплексора принятые информационные символы последовательно подают на вход сумматора по модулю 2, а на второй вход сумматора в том же порядке с анализатора синдрома подают найденные элементы вектора ошибок, в итоге в этом сумматоре ошибки последовательно исправляются в процессе вывода информационных символов.
6) Избыточность (в техническом смысле) для линейного блочного кода равна

| (3.25)
|
Увеличить кодовое расстояние (и корректирующую способность) кода при заданном n удаётся лишь ценой увеличения избыточности, поэтому основной девиз помехоустойчивого кодирования – минимальное значение r при заданных n и  .
.
7) Код, укороченный по сравнению с исходным систематическим кодом, получают следующим образом: для передачи сообщения используют лишь последние m позиций k -разрядного вектора a, а первые k-m позиций заполняют нулями, затем кодируют обычным образом. По линии связи передаётся укороченная комбинация, а в пункте приёма перед кодированием записывают нули на недостающие позиции. При таком укорочении  и r не изменяются, но избыточность возрастает за счёт уменьшения n, поэтому этот способ следует применять лишь в случае крайней необходимости.
и r не изменяются, но избыточность возрастает за счёт уменьшения n, поэтому этот способ следует применять лишь в случае крайней необходимости.



 , по mod2. При декодировании достаточно провести проверку на чётность
, по mod2. При декодировании достаточно провести проверку на чётность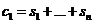 .
.
 0), то это означает, что такая комбинация могла быть передана. Если же проверка не прошла (
0), то это означает, что такая комбинация могла быть передана. Если же проверка не прошла ( всевозможных пятиразрядных комбинаций в кодовую таблицу включим лишь такие комбинации, которые удовлетворяют всем трём заданным проверкам на чётность (количество проверок на чётность всегда равно r). Результаты проведения этих r проверок для конкретной комбинации представим в виде вектора-строки
всевозможных пятиразрядных комбинаций в кодовую таблицу включим лишь такие комбинации, которые удовлетворяют всем трём заданным проверкам на чётность (количество проверок на чётность всегда равно r). Результаты проведения этих r проверок для конкретной комбинации представим в виде вектора-строки  который имеет медицинское название “синдром”, то есть, сочетание признаков, характеризующих определённое состояние. Допустим, для нашего кода мы выбрали следующую систему проверок
который имеет медицинское название “синдром”, то есть, сочетание признаков, характеризующих определённое состояние. Допустим, для нашего кода мы выбрали следующую систему проверок ,
,
 По приведённой таблице (табл. 3.2) легко найти, что
По приведённой таблице (табл. 3.2) легко найти, что  , то есть заданная нами система проверок на чётность (3.11) действительно однозначно определяет систематический корректирующий код, способный не только обнаружить любые однократные и двукратные ошибки, но даже исправлять все однократные ошибки.
, то есть заданная нами система проверок на чётность (3.11) действительно однозначно определяет систематический корректирующий код, способный не только обнаружить любые однократные и двукратные ошибки, но даже исправлять все однократные ошибки.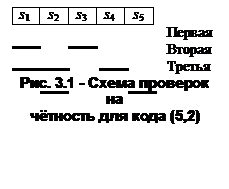 Первый этап декодирования – обнаружение ошибок – фактически сводится к проведению r проверок на чётность (3.11) в принятой кодовой комбинации. Считается, что ошибок нет, если c = 0.
Первый этап декодирования – обнаружение ошибок – фактически сводится к проведению r проверок на чётность (3.11) в принятой кодовой комбинации. Считается, что ошибок нет, если c = 0. ), делаем предположение, что произошла однократная ошибка (гарантированно исправлять ошибки более высоких кратностей этот код все равно не может (3.6)). Рассматривая разные варианты расположения этой одиночной ошибки, видим, что наблюдаемый результат c =011 мог быть получен лишь в случае, когда эта ошибка расположена во втором символе, следовательно, х =10110 и a =10.
), делаем предположение, что произошла однократная ошибка (гарантированно исправлять ошибки более высоких кратностей этот код все равно не может (3.6)). Рассматривая разные варианты расположения этой одиночной ошибки, видим, что наблюдаемый результат c =011 мог быть получен лишь в случае, когда эта ошибка расположена во втором символе, следовательно, х =10110 и a =10. Чтобы не перебирать различные варианты каждый раз при декодировании очередной кодовой комбинации, полезно заранее заготовить таблицу, в которой перечислить все возможные векторы исправляемых ошибок (однократных в нашем примере) и соответствующие им значения вектора-синдрома (табл. 3.3). Если бы код был способен исправлять ещё и все двукратные ошибки, в эту таблицу следовало бы включить дополнительно
Чтобы не перебирать различные варианты каждый раз при декодировании очередной кодовой комбинации, полезно заранее заготовить таблицу, в которой перечислить все возможные векторы исправляемых ошибок (однократных в нашем примере) и соответствующие им значения вектора-синдрома (табл. 3.3). Если бы код был способен исправлять ещё и все двукратные ошибки, в эту таблицу следовало бы включить дополнительно  векторов таких ошибок, в частности 11000, 10100 и т.д.
векторов таких ошибок, в частности 11000, 10100 и т.д.
 k), а правый блок - это единичная матрица (r
k), а правый блок - это единичная матрица (r  ,
, 

 - транспонированная матрица H.
- транспонированная матрица H.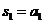 ,
,  , а из соотношений (3.11) находим три проверочных символа, завершая кодирование:
, а из соотношений (3.11) находим три проверочных символа, завершая кодирование:
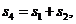
 .
.

 . В итоге получим
. В итоге получим ,
,

 , называемая производящей (генераторной) матрицей данного кода. Обе матрицы связаны уравнением
, называемая производящей (генераторной) матрицей данного кода. Обе матрицы связаны уравнением
 , где Ik - единичная матрица
, где Ik - единичная матрица  . Используя блочные представления обеих матриц, имеем
. Используя блочные представления обеих матриц, имеем
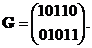
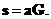

 берут вектор-строку информационных символов ап и по ней заново проводят кодирование, например, по формуле (3.21), получая новое значение вектора-строки проверочных символов
берут вектор-строку информационных символов ап и по ней заново проводят кодирование, например, по формуле (3.21), получая новое значение вектора-строки проверочных символов 



 .
.

