Определение. Число 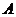 называется пределом функции
называется пределом функции 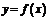 при
при 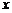 , стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа
, стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа  , найдется такое положительное число
, найдется такое положительное число  (зависящее от
(зависящее от  ;
;  ), что для всех
), что для всех 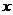 таких, что
таких, что  , верно неравенство:
, верно неравенство:  .
.
Определение. Число 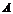 называется пределом функции
называется пределом функции  при
при  , стремящемся к
, стремящемся к 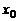 (или в точке
(или в точке  ), если для любого, даже сколь угодно малого положительного числа
), если для любого, даже сколь угодно малого положительного числа  , найдется такое положительное число
, найдется такое положительное число  (зависящее от
(зависящее от  ;
;  ), что для всех
), что для всех 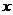 , не равных
, не равных 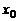 и удовлетворяющих условию
и удовлетворяющих условию  , выполняется неравенство:
, выполняется неравенство:  .
.
Теоремы о пределах:
Функция не может иметь более одного предела.
1. Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.е.  .
.
2. Предел произведений конечного числа функций равен произведению пределов этих функций, т.е.  .
.
3. Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю), т.е. 
 .
.
4. Если 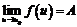 ,
,  , то предел сложной функции
, то предел сложной функции  .
.
5. Если в некоторой окрестности точки  (или при достаточно больших
(или при достаточно больших 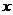 )
)  , то
, то  .
.
Пример. Вычислить 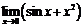 .
.
 .
.
Определение. Функция  называется непрерывной в точке
называется непрерывной в точке  , если она удовлетворяет следующим трем условиям: 1) определена в точке
, если она удовлетворяет следующим трем условиям: 1) определена в точке  (т.е. существует
(т.е. существует  ); 2) имеет конечный предел функции при
); 2) имеет конечный предел функции при  ; 3) этот предел равен значению функции в точке
; 3) этот предел равен значению функции в точке  , т.е.
, т.е.  .
.
Свойства функций, непрерывных в точке:
1. Если функция  и
и 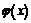 непрерывны в точке
непрерывны в точке  , то их сумма
, то их сумма  , произведение
, произведение  и частное
и частное  (при условии
(при условии  ) являются функциями, непрерывными в точке
) являются функциями, непрерывными в точке  .
.
2. Если функция  непрерывны в точке
непрерывны в точке  и
и  , то существует такая окрестность точки
, то существует такая окрестность точки  , в которой
, в которой 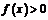 .
.
3. Если функция  непрерывны в точке
непрерывны в точке  , а функция
, а функция  непрерывны в точке
непрерывны в точке  , то сложная функция
, то сложная функция  непрерывна в точке
непрерывна в точке  .
.
Пример. Функция  задана кусочно аналитически, различными аналитическими выражениями для различных подобластей изменения независимой переменной. Найти точки разрыва функции, если они существуют.
задана кусочно аналитически, различными аналитическими выражениями для различных подобластей изменения независимой переменной. Найти точки разрыва функции, если они существуют.

Так как  , и
, и  ,
,  , т.е.
, т.е.  , то в точке
, то в точке 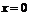 функция
функция 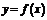 не является непрерывной.
не является непрерывной.
Так как 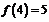 , и
, и  ,
, 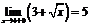 , т.е.
, т.е.  , то в точке
, то в точке  функция
функция  непрерывна.
непрерывна.
30 вопрос тоже.
Определение. Функция  называется непрерывной на промежутке
называется непрерывной на промежутке  , если она непрерывна в каждой точке этого промежутка.
, если она непрерывна в каждой точке этого промежутка.
Свойства функций, непрерывных на отрезке:
1. Если функция  непрерывна на отрезке
непрерывна на отрезке  , то она ограниченна на этом отрезке.
, то она ограниченна на этом отрезке.
2. Если функция 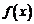 непрерывна на отрезке
непрерывна на отрезке  , то она достигает на этом отрезке наименьшего значения
, то она достигает на этом отрезке наименьшего значения  и наибольшего значения
и наибольшего значения 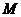 .
.
3. Если функция  непрерывна на отрезке
непрерывна на отрезке  и значение ее на концах отрезка
и значение ее на концах отрезка  и
и  имеют противоположные знаки, то внутри отрезка найдется точка
имеют противоположные знаки, то внутри отрезка найдется точка  такая, что
такая, что 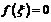 .
.
Пример. Доказать непрерывность функции  .
.
Найдем  . Так как
. Так как  , а
, а  , т.е.
, т.е. 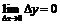 , то функция
, то функция 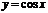 является непрерывной на всей числовой оси.
является непрерывной на всей числовой оси.
ВОПРОС 27.. Основные теоремы о пределах.
- Бесконечно большие и бесконечно малые.
Функция f (x) стремится к бесконечности при x стремящимся к a, если для любого M > 0 можно указать такое значение > 0, что для всех x удовлетворяющих неравенству x a < имеет место неравенство f (x) > M.
lim x a =
- Функция ограниченная при x a.
- Функция ограниченная при x .
- Теорема. Если lim x a f (x)= b, то функция f (x) ограниченная при x a.
- Бесконечно малые и их свойства. lim x a (x)=0
Теорема. 1. Если f (x)= b +, где - б.м. при x a, то lim x a f (x)= b и обратно, если lim x a f (x)= b, то можно записать f (x)= b +(x).
Теорема. 2. Если lim x a (x)=0 и (x) 0, то 1/ .
Теорема. 3. Сумма конечного числа б.м. есть б.м.
Теорема. 4. Произведение б.м. на ограниченную функцию есть б.м.
- Теоремы о пределах.
Теорема. 1. Предел суммы есть сумма пределов.
Теорема. 2. Предел произведения есть произведение пределов.
Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0).
Теорема. 4. Если u (x) z (x) v (x), и lim x a u (x)=lim x a v (x)= b, то lim x a z (x)= b. ("Теорема о двух милиционерах").
| 0.5sin(x) < 0.5 x < 0.5tg(x)
|
- Первый замечательный предел.
- Второй замечательный предел.
Переменная величина
при n ® ¥ имеет предел, заключенный между 2 и 3.
ВОПРОС 32. Бесконечно малые величины, основные теоремы о бесконечно малых.
ВОПРОС 33. Бесконечно большие величины, связь бесконечно малых с бесконечными величинами.
ВОПРОС 36.. Дифференцируемость функции, первый дифференциал и производная первого порядка.. Связь непрерывности и дифференцируемости
Пусть функция задана в некоторой области, и -- внутренняя точка этой области. Пусть -- произвольная точка этой же области. Разность называется приращением аргумента;, где. Разность значений функции называется приращением, или полным приращением функции в точке, соответствующим приращению аргумента; -- это функция от точки и приращения.
Предположим, что приращение функции можно представить в виде
(7.2
где -- некоторые числа. Подчеркнём, что эти числа не зависят от, но могут измениться, если сменить точку. Относительно величины мы предположим, что это функция, при базе являющаяся величиной большего порядка малости, чем. Это означает, если вспомнить определение бесконечно малой величины большего порядка малости относительно другой бесконечно малой, что
Заметим, что сумма всех слагаемых левой части (7.2), кроме последнего, -- это линейная функция от приращения аргумента, если точка фиксирована. Условие большей малости последнего слагаемого (7.2) относительно означает, что эта линейная функция -- главная часть приращения функции.
Определение 7.11 Если указанное представление (7.2) имеет место, то функцию называют дифференцируемой в точке, а линейную относительно функцию
то есть главную линейную часть приращения функции, -- дифференциалом функции в точке.
Если функция является дифференцируемой в любой точке открытой области, то функцию называют дифференцируемой в области.
Таким образом, приращение дифференцируемой функции можно представить в виде суммы дифференциала, то есть линейной части приращения, и остатка, который имеет более высокий порядок малости, чем приращение:
Теорема 7.8 Дифференцируемая в точке функция является непрерывной в этой точке.
Доказательство. Действительно, если, то стремятся к 0 все слагаемые дифференциала: они имеют вид; множитель не зависит от, то есть постоянен, а, поскольку Величина также стремится к 0, так как имеет даже больший порядок малости, чем. Значит,. Но условие как раз и означает, что при, то есть что функция непрерывна в точке.
ВОПРОС 37. Правила дифференцирования. Таблица производных.

ВОПРОС 39. Основные теоремы дифференциального исчисления (теоремы Ферма, Ролля).
ТеоремаФерма
Пусть функция  или
или  в т.
в т. 
Пусть, для определённости,  (рис. 10.1), тогда
(рис. 10.1), тогда  при
при 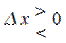 и
и 
Согласно определению производной имеем 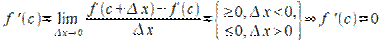

Рис. 10.1
Геометрическоеистолкованиетеоремывытекаетизгеометрическогосмыслапроизводной: касательная к графику функции  в точке с абсциссой
в точке с абсциссой  параллельна оси
параллельна оси  .
.
Теорема Ролля
Пусть функция  . Тогда
. Тогда 
Из условия  следуетпосвойству10непрерывныхна
следуетпосвойству10непрерывныхна  функций, что
функций, что 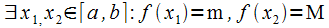 .
.
Существует две возможности:
1)  ;
;
2)  в силу
в силу  .
.
Пусть  , тогда согласно теореме Ферма
, тогда согласно теореме Ферма  .
.
Данная теорема обладает таким же геометрическим истолкованием, что и теорема Ферма.
ВОПРОС 40. Теорема Лагранжа (формула конечных приращений). Связь теоремы Коши с теоремой Лагранжа.
Формула конечных приращений или теорема Лагра́нжа о среднем значении утверждает, что если функция  непрерывна на отрезке
непрерывна на отрезке  и дифференцируема в интервале
и дифференцируема в интервале  , то найдётся такая точка
, то найдётся такая точка  , что
, что 
Геометрически это можно переформулировать так: на отрезке  найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.
найдётся точка, в которой касательная параллельна хорде, проходящей через точки графика, соответствующие концам отрезка.
Вопрос 41.Теорема Коши́
Теорема Коши о среднем значении является обобщением теоремы Лагранжа о конечных приращениях
Пусть на отрезке определены две непрерывные фунции  . Пусть также
. Пусть также  существует конечная или бесконечная производная f'(x), а функция g дифференцируема, то есть
существует конечная или бесконечная производная f'(x), а функция g дифференцируема, то есть  , и
, и 
Тогда 
Пример. Проверить, что функции  и
и  на отрезке
на отрезке 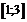 удовлетворяют условиям Коши.
удовлетворяют условиям Коши.
Функции  и
и 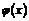 непрерывны при всех
непрерывны при всех 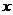 , а значит, и на отрезке
, а значит, и на отрезке 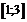 ; их производные
; их производные  и
и  существуют везде; кроме того,
существуют везде; кроме того,  на заданном отрезке не обращается в нуль.
на заданном отрезке не обращается в нуль.
Следовательно, к данным функциям применима теорема Коши: 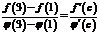 , т.е.
, т.е.  , откуда находим два значения
, откуда находим два значения  :
:  ,
,  .
.
Из полученных значений только  удовлетворяет условию задачи, так как
удовлетворяет условию задачи, так как  является внутренней точкой отрезка
является внутренней точкой отрезка  .
.
Вопрос 43. Формула Тейлора
Формула Тейлора. Пусть функция  имеет в точке
имеет в точке  и некоторой ее окрестности производные порядка
и некоторой ее окрестности производные порядка  . Пусть
. Пусть 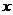 - любое значение аргумента из указанной окрестности,
- любое значение аргумента из указанной окрестности,  . Тогда между точками
. Тогда между точками  и
и 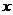 найдется точка
найдется точка  така, что справедлива формула Тейлора
така, что справедлива формула Тейлора 
 .
.



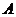 называется пределом функции
называется пределом функции 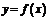 при
при 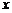 , стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа
, стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа  , найдется такое положительное число
, найдется такое положительное число  (зависящее от
(зависящее от  ;
;  ), что для всех
), что для всех 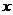 таких, что
таких, что  , верно неравенство:
, верно неравенство:  .
.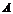 называется пределом функции
называется пределом функции  при
при  , стремящемся к
, стремящемся к 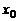 (или в точке
(или в точке  ), если для любого, даже сколь угодно малого положительного числа
), если для любого, даже сколь угодно малого положительного числа  (зависящее от
(зависящее от  ), что для всех
), что для всех  , выполняется неравенство:
, выполняется неравенство:  .
. .
. .
.
 .
.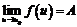 ,
,  , то предел сложной функции
, то предел сложной функции  .
. (или при достаточно больших
(или при достаточно больших  , то
, то  .
.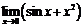 .
. .
. называется непрерывной в точке
называется непрерывной в точке  ); 2) имеет конечный предел функции при
); 2) имеет конечный предел функции при  ; 3) этот предел равен значению функции в точке
; 3) этот предел равен значению функции в точке  .
. и
и 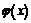 непрерывны в точке
непрерывны в точке  , произведение
, произведение  и частное
и частное  (при условии
(при условии  ) являются функциями, непрерывными в точке
) являются функциями, непрерывными в точке  непрерывны в точке
непрерывны в точке  , то существует такая окрестность точки
, то существует такая окрестность точки 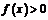 .
. непрерывны в точке
непрерывны в точке  , а функция
, а функция  непрерывны в точке
непрерывны в точке  , то сложная функция
, то сложная функция  непрерывна в точке
непрерывна в точке  задана кусочно аналитически, различными аналитическими выражениями для различных подобластей изменения независимой переменной. Найти точки разрыва функции, если они существуют.
задана кусочно аналитически, различными аналитическими выражениями для различных подобластей изменения независимой переменной. Найти точки разрыва функции, если они существуют.
 , и
, и  ,
,  , т.е.
, т.е.  , то в точке
, то в точке 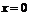 функция
функция 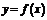 не является непрерывной.
не является непрерывной.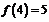 , и
, и  ,
, 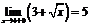 , т.е.
, т.е.  , то в точке
, то в точке  функция
функция  непрерывна.
непрерывна. , если она непрерывна в каждой точке этого промежутка.
, если она непрерывна в каждой точке этого промежутка. непрерывна на отрезке
непрерывна на отрезке  , то она ограниченна на этом отрезке.
, то она ограниченна на этом отрезке.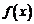 непрерывна на отрезке
непрерывна на отрезке  , то она достигает на этом отрезке наименьшего значения
, то она достигает на этом отрезке наименьшего значения  и наибольшего значения
и наибольшего значения 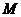 .
. и значение ее на концах отрезка
и значение ее на концах отрезка  и
и  имеют противоположные знаки, то внутри отрезка найдется точка
имеют противоположные знаки, то внутри отрезка найдется точка  такая, что
такая, что 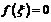 .
. .
. . Так как
. Так как  , а
, а  , т.е.
, т.е. 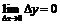 , то функция
, то функция 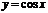 является непрерывной на всей числовой оси.
является непрерывной на всей числовой оси.
 или
или  в т.
в т. 
 (рис. 10.1), тогда
(рис. 10.1), тогда  при
при 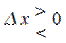 и
и 
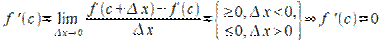

 в точке с абсциссой
в точке с абсциссой  параллельна оси
параллельна оси  .
. . Тогда
. Тогда 
 следуетпосвойству10непрерывныхна
следуетпосвойству10непрерывныхна  функций, что
функций, что 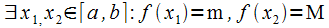 .
. ;
; в силу
в силу  .
. , тогда согласно теореме Ферма
, тогда согласно теореме Ферма  .
. непрерывна на отрезке
непрерывна на отрезке  и дифференцируема в интервале
и дифференцируема в интервале  , то найдётся такая точка
, то найдётся такая точка  , что
, что 
 . Пусть также
. Пусть также  существует конечная или бесконечная производная f'(x), а функция g дифференцируема, то есть
существует конечная или бесконечная производная f'(x), а функция g дифференцируема, то есть  , и
, и 

 и
и  на отрезке
на отрезке 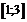 удовлетворяют условиям Коши.
удовлетворяют условиям Коши. и
и 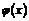 непрерывны при всех
непрерывны при всех  и
и  существуют везде; кроме того,
существуют везде; кроме того,  на заданном отрезке не обращается в нуль.
на заданном отрезке не обращается в нуль.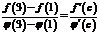 , т.е.
, т.е.  , откуда находим два значения
, откуда находим два значения  :
:  ,
,  .
. удовлетворяет условию задачи, так как
удовлетворяет условию задачи, так как  является внутренней точкой отрезка
является внутренней точкой отрезка  .
. и некоторой ее окрестности производные порядка
и некоторой ее окрестности производные порядка  . Пусть
. Пусть  . Тогда между точками
. Тогда между точками  така, что справедлива формула Тейлора
така, что справедлива формула Тейлора 
 .
.


