

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...
Топ:
Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь...
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Интересное:
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Уравнение вида
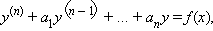
|
где a 1, …, an – некоторые постоянные, называется линейным дифференциальным уравнением с постоянными коэффициентами.
Всякое решение однородного уравнения первого порядка
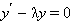
|
имеет вид
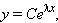
|
где C – постоянная.
Уравнение вида
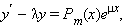
|
где Pm (x) – многочлен степени m, μ – постоянная, имеет частное решение вида
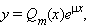
|
если μ ≠ λ, и вида
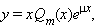
|
если μ = λ. Здесь Qm (x) – многочлен степени m.
В общем случае у однородного линейного дифференциального уравнения с постоянными коэффициентами 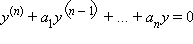 имеется так называемое характеристическое уравнение
имеется так называемое характеристическое уравнение 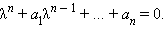 Корни этого уравнения – характеристические числа – являются показателями степеней слагаемых, входящих в решение. Если среди корней уравнения
Корни этого уравнения – характеристические числа – являются показателями степеней слагаемых, входящих в решение. Если среди корней уравнения 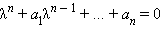 нет кратных, то решением однородного уравнения является функция вида
нет кратных, то решением однородного уравнения является функция вида 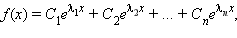 где все
где все 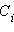 – некоторые константы, зависящие от начальных условий. Количество слагаемых в этой функции совпадает со степенью дифференциального уравнения. Если же, скажем,
– некоторые константы, зависящие от начальных условий. Количество слагаемых в этой функции совпадает со степенью дифференциального уравнения. Если же, скажем, 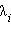 – корень характеристического уравнения кратности m, то соответствующее слагаемое принимает вид
– корень характеристического уравнения кратности m, то соответствующее слагаемое принимает вид 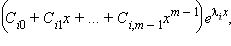 а общее количество слагаемых, входящих в решение однородного дифференциального уравнения уменьшается на m – 1.
а общее количество слагаемых, входящих в решение однородного дифференциального уравнения уменьшается на m – 1.
Метод вариации произвольных постоянных
Этот метод основан на том, что форма записи решения неоднородного уравнения такая же, что и у соответствующего однородного, с той лишь разницей, что произвольную постоянную С следует считать некоторой функцией переменной t, С = С(t), то есть x(t)=C(t)e (3.5)
Функция C(t) должна быть такой, чтобы при подстановке (3.5) в уравнение (3.1) последнее обращалось в тождество. Подставляя x(t) и C'(t)e =f(t) или C'{t)=f(t)e
Интегрируя, находим выражение для C(t): (3.6)
|
|
Подставляя полученное выражение в (3.4), получаем общее решение линейного неоднородного уравнения (3.1) в виде. (3.7)
Заметим, что первое слагаемое в формуле (3.7) является частным решением линейного неоднородного уравнения (3.1), в чем можно убедиться непосредственной проверкой. Второе слагаемое является общим решением соответствующего однородного уравнения (3.3). Этот результат подтверждает известное свойство решений неоднородного уравнения.
Приведенные рассуждения позволяют сформулировать алгоритм решения уравнения (3.1).
Системы обыкновенных дифференциальных уравнений
Рассмотрим систему обыкновенных дифференциальных уравнений n–го порядка
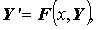 или
или 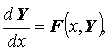
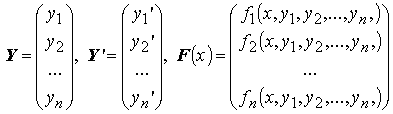
Задачей Коши для для этой системы называется следующая задача: найти такое решение Y = Y (x) системы Y ' = F (x, Y), что Y (x 0)= Y 0, где Y 0 — некоторый постоянный вектор.
Вектор-функция Y = Y (x, С), зависящая от произвольного вектора С, называется общим решением системы, если:
— при любом векторе C, вектор-функция Y (x, С) является решением системы;
— какова бы ни была начальная точка ((x 0, Y 0), существует такой вектор С (0), что Y (x (0), С (0)) = Y 0.
|
|
|

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Индивидуальные очистные сооружения: К классу индивидуальных очистных сооружений относят сооружения, пропускная способность которых...

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!