Пусть нам известно значение функции y 0 =f(x 0 ) и ее производной y 0 ' = f '(x 0) в точке x 0. Покажем, как найти значение функции в некоторой близкой точке x.
Как мы уже выяснили приращение функции Δ y можно представить в виде суммы Δ y = dy +α·Δ x, т.е. приращение функции отличается от дифференциала на величину бесконечно малую. Поэтому, пренебрегая при малых Δ x вторым слагаемым в приближенных вычислениях, иногда пользуются приближенным равенством Δ y ≈ dy илиΔ y» f '(x 0)·Δ x.
Т.к., по определению, Δ y = f (x) – f (x 0), то f(x) – f(x 0) ≈ f '(x 0)·Δ x. Откуда
f(x) ≈ f(x 0) + f '(x 0)·Δ x
Основные теоремы о дифференцируемых функциях
1.Теорема. Ролля. Если функция g (x) непрерывна на отрезке [ a, b ], дифференцируема во всех внутренних точках этого отрезка и на концах обращается в нуль g (a)= g (b)=0, то существует по крайней мере одна точка a < c < b в которой производная g ¢ обращается в нуль g ¢(c)=0.
Доказательство. Так как функция непрерывна на [ a, b ], то она имеет на этом отрезке наибольшее (M) и наименьшее значение m. Пусть g (c) - наибольшее значение.
Отсюда
| | g (c +D x) - g (c)
D x
| £ 0, D x > 0
| |
| | g (c +D x) - g (c)
D x
| ³ 0, D x < 0
| |
Переходим к пределу и получаем одновременно g ¢(с) ³ 0 и g ¢(с) £ 0, следовательно, g ¢(с)=0.
Пример функции, для которой не выполняется условие теоремы, поэтому производная внутри отрезка в 0 не обращается
2. Теорема. Лагранжа. Если функция g (x) непрерывна на отрезке [ a, b ], дифференцируема во всех внутренних точках этого отрезка, то существует по крайней мере одна точка a < c < b в которой выполняется равенство
| g (b)- g (a)= g ¢(c)(b - a)
| |
Доказательство. Применим теорему Ролля к функции
где
| Q =(g (b)- g (a))/(b - a)
| |
3. Теорема. Коши. Если функции g (x) и h (x) непрерывны на отрезке [ a, b ], дифференцируемы во всех внутренних точках этого отрезка, причем h ¢(x) ¹ 0 внутри отрезка [ a, b ], то существует точка a < c < b в которой выполняется равенство
| | g (b)- g (a)
h (b)- h (a)
| =
| g ¢(c)
h ¢(c)
| | |
Доказательство. Применим теорему Ролля к функции
| g (x)- g (a)-(h (x)- h (a)) Q,
| |
где
| Q =(g (b)- g (a))/(h (b)- h (a))
| |
4. Теорема. Лопиталя. Пусть функции g (x) и h (x) на некотором отрезке [ a, b ] удовлетворяют условиям теоремы Kоши и обращаются в 0 в точке x = a, т.е. g (a)= h (a)=0, тогда если существует предел отношения g ¢(x)/ h ¢(x) при x ® a, то существует и
причем
| | lim x ® a
| g ¢(x)/ h ¢(x)=
| lim x ® a
| g (x)/ h (x).
| |
Правило Лопиталя
Пусть функции f(x) и g(x) дифференцируемы в некоторой окрестности точки a, за исключением, быть может, самой точки a, и пусть 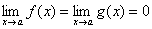 или
или 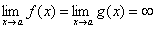 . Тогда, если существует предел отношения производных этих функций
. Тогда, если существует предел отношения производных этих функций 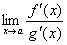 , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем
, то существует и предел отношения самих функций f(x)/g(x) при x→а, причем
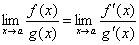
| (1)
|
Таким образом, коротко правило Лопиталя можно сформулировать следующим образом: предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.
Замечание. Отметим, что формула (1) справедлива только в том случае, если предел, стоящий справа, существует. Может случиться, что предел, стоящий слева существует, в то время как предел, стоящий в правой части равенства, не существует.
Например, найти 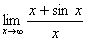 . Этот предел существует
. Этот предел существует 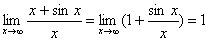 . Но отношение производных (1+cosx)/1=1+cos x при x→∞ не стремится ни к какому пределу.
. Но отношение производных (1+cosx)/1=1+cos x при x→∞ не стремится ни к какому пределу.
Заметим, что если отношение производных опять представляет собой неопределенность вида 0/0 или ∞/∞, то можно снова применить сформулированную теорему, то есть перейти к отношению вторых производных и так далее.
Вспомним, что к этим двум случаям сводятся случаи других неопределенностей: ∞·∞; 0·∞.
Для раскрытия неопределенностей 1∞, 10, ∞0 нужно прологарифмировать данную функцию и найти предел ее логарифма.
Монотонность ф-ии
Возрастающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) - функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
Экстремумы
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами.



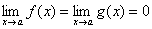 или
или 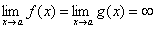 . Тогда, если существует предел отношения производных этих функций
. Тогда, если существует предел отношения производных этих функций 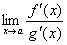 , то существует и предел отношения самих функций f(x)/g(x) при x→а, причем
, то существует и предел отношения самих функций f(x)/g(x) при x→а, причем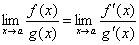
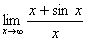 . Этот предел существует
. Этот предел существует 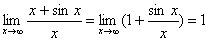 . Но отношение производных (1+cosx)/1=1+cos x при x→∞ не стремится ни к какому пределу.
. Но отношение производных (1+cosx)/1=1+cos x при x→∞ не стремится ни к какому пределу.


