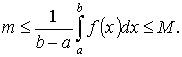Если существует конечный предел I интегральной суммы при λ → 0, и он не зависит от способа выбора точек ξ i, способа разбиения отрезка, то этот предел называется определенным интегралом от функции f (x)по отрезку [ a, b ] и обозначается следующим образом:
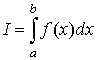 ,
,
или
 .
.
В этом случае функция f (x) называется интегрируемой на [ a, b ]. Числа a и b называются соответственно нижним и верхним пределами интегрирования, f (x) – подынтегральной функцией, х – переменной интегрирования. Следует заметить, что не имеет значения, какой буквой обозначена переменная интегрирования определенного интеграла
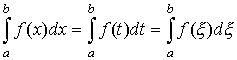 ,
,
поскольку смена обозначений такого рода никак не влияет на поведение интегральной суммы
64. Теорема. Производная интеграла по переменной верхней границе равна подынтегральной функции, в которой переменная интегрирования заменена верхней границей.
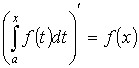 .
.
Из вышесказанного имеем
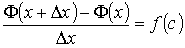 ,
,
где с Î[ х, х + Δ х ]. Переходя к пределу при Δ х → 0 и учитывая, что
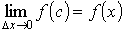
в силу непрерывности функции f (x), получаем требуемое условие.
Следствие. Если функция y = f (х) непрерывна на отрезке [ a, b ], то для этой функции существует первообразная на отрезке [ а, b ].
Действительно, примером первообразной для f (x) является функция Ф (х).
Формула Ньютона—Лейбница
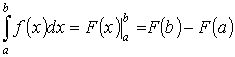 .
.
66.
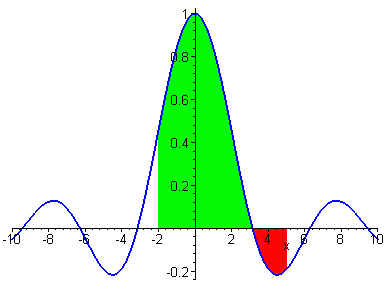
1.Определённый интеграл численно равен площади криволинейной трапеции, ограниченной графиком функции у = f (x), осью абсцисс, и прямыми х = а, х = b.
2. Если нижний и верхний пределы интегрирования поменять местами, то значение определённого интеграла изменится на противоположное
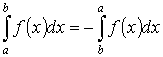
Доказательство.
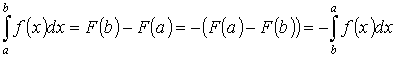 .
.
3. Если промежуток интегрирования стянут в точку, фигура под кривой стягивается в отрезок, площадь которого равна нулю
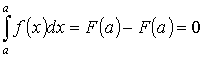 .
.
4. Постоянный множитель можно выносить за знак интеграла
, 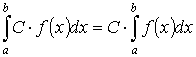
где С — некоторое число.
Доказательство.
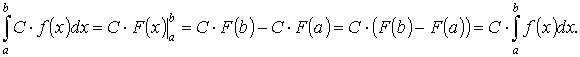
5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций:
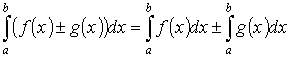 ,
,
Это свойство остается справедливым для любого конечного числа слагаемых.
Доказательство.
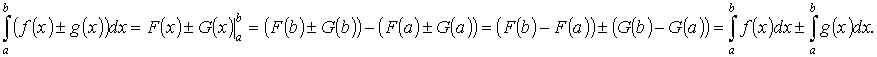
6. Если промежуток интегрирования разбит на части, то интеграл по всему отрезку равен сумме интегралов по каждой части.
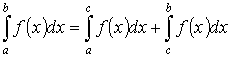 .
.
Доказательство. Пусть а < с < b и функция f (x) неотрицательна на [ a, b ]. Согласно геометрическому свойству определенного интеграла 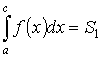 ,
, 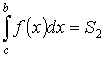 есть площади соответствующих криволинейных трапеций. Тогда при сделанных предположениях имеем равенство между площадями S = S 1 + S 2.
есть площади соответствующих криволинейных трапеций. Тогда при сделанных предположениях имеем равенство между площадями S = S 1 + S 2.
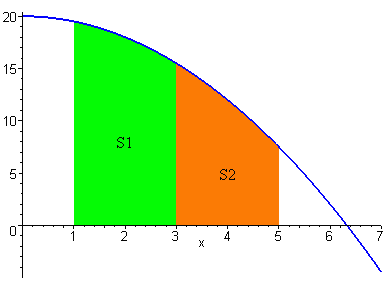
7Если на отрезке [ a, b ], где а < b, имеет место неравенство 0 ≤ f (x) ≤ g (x), то
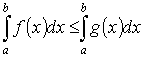 .
.
Обе части неравенства можно проинтегрировать, при этом смысл неравенства остаётся прежним.
Доказательство. Пусть фиксированы разбиение отрезка [ a, b ] и выбор точек x 1, x 2,…, xn на каждом из отрезков разбиения. Тогда из неравенства f (x) ≤ g (x) вытекает аналогичное неравенство для интегральных сумм:
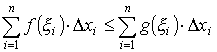 .
.
Переходя к пределу при max Δ xi → 0, получим рассматриваемое неравенство для интегралов.
Следствие. Пусть на отрезке [ a, b ] где а < b, имеют место неравенства m ≤ f (x) ≤ M, где m и М — некоторые числа. Тогда
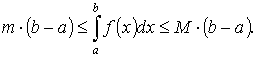


67. Теорема о среднем. Если функция y = f (x) непрерывна на отрезке [ a, b ], где а < b, то найдется такое значение c Î [ a, b ], что
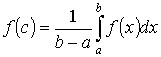 .
.
По свойству функции, непрерывной на отрезке, для произвольного значения х Î [ a, b ] вверны неравенства m ≤ f (x) ≤ M, где m и М — наименьшее и наибольшее значения функции на [ a, b ]. Тогда,
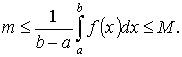
Функция, непрерывная на отрезке, принимает любое значение, заключенное между ее наименьшим и наибольшим значениями. Поэтому, в частности, найдется такое число с Î [ a, b ], что
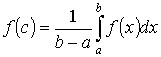 ,что и требовалось доказать.
,что и требовалось доказать.
Геометрический смысл теоремы о среднем. Пусть f (x) ≥ 0 на [ a, b ]. По теореме о среднем найдется такая точка, из отрезка [ a, b ], что площадь под кривой y = f (x)
на отрезке [ a, b ] равна площади прямоугольника со сторонами f (с) и (b - а). 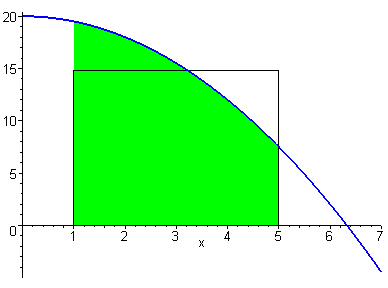


68. 


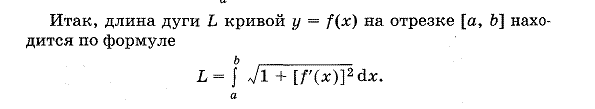


69. 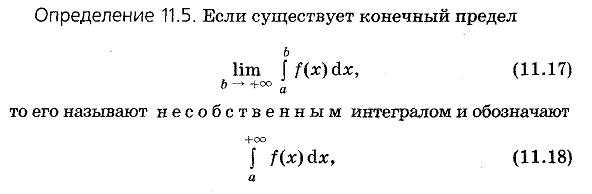



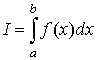 ,
, .
.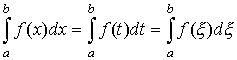 ,
,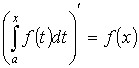 .
.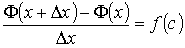 ,
,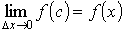
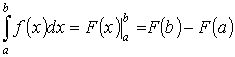 .
.
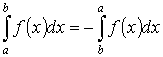
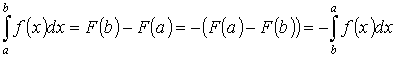 .
.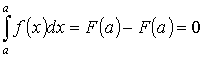 .
.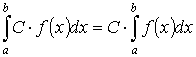
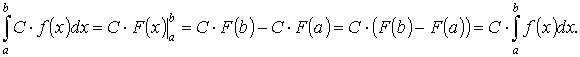
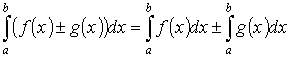 ,
,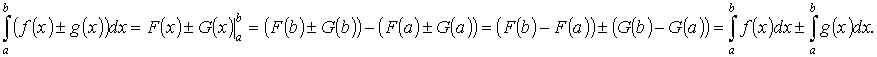
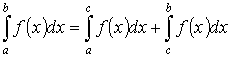 .
.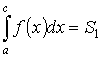 ,
, 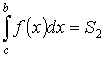 есть площади соответствующих криволинейных трапеций. Тогда при сделанных предположениях имеем равенство между площадями S = S 1 + S 2.
есть площади соответствующих криволинейных трапеций. Тогда при сделанных предположениях имеем равенство между площадями S = S 1 + S 2.
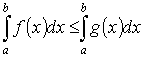 .
.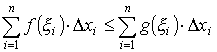 .
.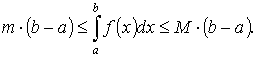


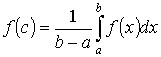 .
.