

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Особенности сооружения опор в сложных условиях: Сооружение ВЛ в районах с суровыми климатическими и тяжелыми геологическими условиями...
Топ:
Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь...
Комплексной системы оценки состояния охраны труда на производственном объекте (КСОТ-П): Цели и задачи Комплексной системы оценки состояния охраны труда и определению факторов рисков по охране труда...
Эволюция кровеносной системы позвоночных животных: Биологическая эволюция – необратимый процесс исторического развития живой природы...
Интересное:
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Основы линейной алгебры
Одной из основных задач линейной алгебры является решение систем линейных алгебраических уравнений. К таким системам сводятся многие задачи математического моделирования физических и технологических процессов при их дискретизации, т.е. представления соответствующих дифференциальных уравнений через конечные разности или конечные элементы. Используя алгебру матриц, система линейных алгебраических уравнений представляется в наиболее простой и компактной форме
А X = B, (2.1)
где А – матрица коэффициентов системы уравнений (основная матрица), X – матрица-столбец неизвестных, В – матрица-столбец свободных членов. Поэтому удобно проводить исследование решений системы (2.1), используя язык матриц. Рассмотрим элементы алгебры матриц.
Понятие матрицы
Определение 2.1. Матрицей называется прямоугольная таблица из n × m чисел, которая содержит m строк и n столбцов.
Обозначения:  или
или  . (2.2)
. (2.2)
Либо кратко [ а ij ] (i = 1,2,…, n; j = 1,2,..,m). В этом случае имеется в виду, что матрица имеет размерность n × m. Матрицы обозначают заглавными латинскими буквами А, В, С, Е,... Числа aij называются элементами матрицы, где первый индекс i означает номер строки, а второй j - номер столбца.
Если в квадратной матрице все элементы главной диагонали равны единице, а все остальные равны нулю, то её называют единичной матрицей. Она обозначается буквой Е и имеет вид
 . (2.3)
. (2.3)
Определение 2.2. Две матрицы А и В называются равными, если они имеют одинаковое количество строк и столбцов и соответствующие элементы которых совпадают.
Матрица, в которой все элементы равны нулю, называется нуль-матрицей или нулевой. Её обозначают буквой О.
Если матрица состоит только из одной строки, то она называется матрицей-строкой. Матрица, состоящая из одного столбца называется матрицей-столбцом.
|
|
Если в матрице А поменять строки на столбцы, а столбцы – на соот-ветствующие строки, то полученную матрицу называют транспонированной и обозначают АT.
Действия над матрицами
Сложение.
Операция сложения матриц вводится только для матриц одинаковых размеров.
Определение 2.3. Суммой двух матриц  и
и  называется матрица
называется матрица  такая, что
такая, что  .
.
Пример
 +
+  =
=  .
.
Аналогично определяется разность матриц.
Умножение на число
Определение 2.4. Произведеним матрицы  на число k называется матрица
на число k называется матрица  такая, что
такая, что 
Пример
А =  , k = 2, A∙k =
, k = 2, A∙k = 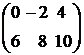 .
.
Разность матриц А – В можно определить так: А – В = А +(– В).
Операции сложения и умножения матрицы на число обладают следующими свойствами:
1. А + В = В + А; 5. 1 ∙ А =А;
2. А + (В + С) = (А + В) + С; 6. α ∙ (А + В)= α ∙А + α ∙В;
3. А + О = А; 7. (α + β)∙А = α ∙А + β ∙А;
4. А – А = О; 8. α ∙ (β ∙ А) = (α ∙ β) ∙ А,
где А, В, С – матрицы, α, β – числа.
Произведение матриц.
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Определение 2.5. Произведением матрицы  на матрицу
на матрицу  называется матрица
называется матрица  такая, что
такая, что
 ,
,
т.е. элемент i-ой строки и k го столбца матрицы произведения С равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы k-го столбца матрицы В.
Получение элемента  схематично изображается так:
схематично изображается так:

Если матрицы А и В квадратные одного размера, то произведение А∙В и В∙А всегда существуют. Легко показать, что А∙Е = Е∙А = А, где А – квадратная матрица, Е – единичная матрица того же размера.
Пример
 ,
,  . Тогда произведение матриц А
. Тогда произведение матриц А  В определяется следующим образом:
В определяется следующим образом:
А  В =
В =  ∙
∙  =
=  =
=  .
.
При этом произведение В  А не определено, так как число столбцов матрицы В (3) не совпадет с числом строк матрицы А (2).
А не определено, так как число столбцов матрицы В (3) не совпадет с числом строк матрицы А (2).
Матрицы А и В называются перестановочными, если АВ = ВА.
|
|
Умножение матриц обладает следующими свойствами
1. А ∙ (В ∙ С)= (А ∙ В) ∙ С; 3. (А + В) ∙ С = А∙С + В∙С;
2. А ∙ (В + С) = А∙В + А∙С; 4. α ∙ (А ∙ В)= (α∙ А) ∙ В,
если, конечно, написанные суммы и произведения матриц имеют смысл.
Для операции транспонирования верны свойства:
1. (А+В) Т = АТ + ВТ; 2. (А∙В) Т = АТ ∙ ВТ.
Определители
Любой квадратной матрице А порядка n ставится в соответствие некоторое число, называемое определителем этой матрицы.
Обозначение: det A (или | A | или ΔA).
Определение 2.6. Определителем матрицы 1–го порядка (т.е. матрицы, состоящей из одного элемента, одного числа) называется само число, составляющее заданную матрицу.
Определение 2.7. Определителем матрицы 2-го порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом:
 .
.
Определение 2.8. Определитель третьего порядка вычисляется по формуле:

При вычислении определителей 3-го порядка удобно пользоваться правилом треугольников, которое символически можно представить так:

Примеры. Вычислить определители третьего порядка
1. 

2. 
Для вычисления определителя матриц 4-го и более высоких порядков рассмотрим дополнительные понятия. Рассмотрим определитель матрицы А n- го порядка
Δn =  .
.
Определение 2.9. Выделим в нём какой-либо элемент aij и вычеркнем i -ю строку и j -й столбец, на пересечении которых расположен этот элемент. Полученный определитель (n-1) –го порядка называется минором Mij элемента aij определителя Δn.
Определение 2.10. Наибольший порядок миноров матрицы А, отличных от нуля, называется рангом матрицы.
Определение 2.11. Алгебраическим дополнением элемента aij определителя Δn называется число
Aij = (-1) i+j Mij.
Определение 2.12. Определителем n-го порядк а Δn вычисляетсясуммой произведения элементов любой строки (столбца)на их алгебраические дополнения
Δn =  =
=  , 1 ≤ i,k ≤ n. (2.4)
, 1 ≤ i,k ≤ n. (2.4)
Пример. Вычислим определитель 4-го порядка  с помощью разложения по 2-му столбцу. Для этого найдем
с помощью разложения по 2-му столбцу. Для этого найдем  и
и 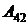 :
:

Следовательно, 
Квадратная матрица А называется невырожденной, если определитель Δ = det A ≠ 0. В противном случае (Δ = 0) матрица А называется вырожденной.
Определение 2.13. Матрица А-1 называется обратной матрице А, если выполняется условие
А А-1 = А-1 А = Е, (2.5)
|
|
где Е – единичная матрица того же порядка, что и матрица А. Отметим, что для вырожденной матрицы обратная матрица не существует.
Основные свойства определителей.
1. Определитель, имеющий нулевую строку (столбец), равен нулю.
2. При перестановке двух строк (столбцов) определитель меняет знак.
3. Определитель, имеющий две одинаковы строки (одинаковые столбцы),
равен нулю.
4. Общий множитель любой строки (столбца) можно вынести за знак оп-
ределителя.
5. Если каждый элемент некоторой строки (столбца) определителя Δn представлен в виде суммы двух слагаемых, то этот определитель равен сумме двух определителей. Поясним это на примере определителя 3-го порядка



6. Величина определителя не изменится, если к элементам одной строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.
7. При транспонировании матрицы её определитель не меняется.
Примеры для самостоятельного решения
Вычислить определители
1)  . 2)
. 2)  . 3)
. 3)  .
.
4)  . 5)
. 5) 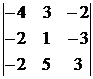 . 6)
. 6)  .
.
Метод Крамера.
Другой метод решения системы линейных алгебраических уравнений основан на теореме Крамера.
Система из n уравнений с n неизвестными
 (2.9)
(2.9)
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
xi = Di/D, (2.10)
где D = det A, а Di – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
Di =  .
.
Формулы вычисления неизвестных (2.8) носят название формул Крамера. Таким образом, правило Крамера позволяет найти единственное решение системы (2.3) или сделать вывод о существовании бесконечного числа решений либо об их отсутствии:
1) Если 
 система (2.3) имеет единственное решение, определяемое по формулам:
система (2.3) имеет единственное решение, определяемое по формулам:  .
.
2) Если  =
=  = 0, система имеет бесконечно много решений.
= 0, система имеет бесконечно много решений.
3) Если  = 0, а хотя бы один из
= 0, а хотя бы один из 
 система не имеет решений.
система не имеет решений.
Если система однородна, т.е. bi = 0, то при D¹0 система имеет единственное нулевое решение x1 = x2 = … = xn = 0.
Пример. Найти решение системы уравнений: 
D =  = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
D1 =  = (28 – 48) – (42 – 32) = -20 – 10 = -30. x1 = D1/D = 1;
= (28 – 48) – (42 – 32) = -20 – 10 = -30. x1 = D1/D = 1;
D2 =  = 5(28 – 48) – (16 – 56) = -100 + 40 = -60. x2 = D2/D = 2;
= 5(28 – 48) – (16 – 56) = -100 + 40 = -60. x2 = D2/D = 2;
D3 =  = 5(32 – 42) + (16 – 56) = -50 – 40 = -90. x3 = D3/D = 3.
= 5(32 – 42) + (16 – 56) = -50 – 40 = -90. x3 = D3/D = 3.
|
|
Метод Гаусса
В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.
Рассмотрим систему линейных уравнений:

Разделим обе части 1–го уравнения на a11 ¹ 0, затем:
1) умножим на а21 и вычтем из второго уравнения
2) умножим на а31 и вычтем из третьего уравнения
и т.д.
 , где d1j = a1j/a11, j = 2, 3, …, n+1.
, где d1j = a1j/a11, j = 2, 3, …, n+1.
dij = aij – ai1d1j i = 2, 3, …, n; j = 2, 3, …, n+1.
Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.
Пример. Решить систему линейных уравнений методом Гаусса.

Составим расширенную матрицу системы.
А* = 
Таким образом, исходная система может быть представлена в виде:
 , откуда получаем: x3 = 2; x2 = 5; x1 = 1.
, откуда получаем: x3 = 2; x2 = 5; x1 = 1.
Примеры для самостоятельного решения
Решить системы линейных уравнений двумя способами: методом Крамера и методом Гаусса.
1)  . 2)
. 2)  . 3)
. 3)  .
.
4)  . 5)
. 5) 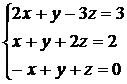 . 6)
. 6)  .
.
Решние СЛАУ методом Крамера
По методу Крамера решение система n линейных уравнений c n неизвестными
 ,
,
если определитель матрицы системы не равен нулю (D = det A ≠ 0) определяется отношениями
xi = Di/D, (2.10)
где D = det A, а Di – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
Таким образом, по правилу Крамера необходимо сформировать соответствующие матрицы, вычислить их определители DI и D, а неизвестные находятся по формуле (2.10). Решение СЛАУ методом Крамера рассмотрим на примере.
Пример. Найти решение системы уравнений

Найдём определитель основной матрицы

Матрица D невырожденная, значит, решение существует и единственно. Найдем вспомогательные матрицы:

 неизвестные определяются по формуле (2.10)
неизвестные определяются по формуле (2.10)

Функция linsolve
Синтаксис данной функции такой же, как и функции solve. С помощью этой функции рассмотрим решение предыдущего примера.
Необходимо обратиться к основному меню Уравнения и перейти к вкладке Solve Linear System…

возникает вспомогательное окно, в котором необходимо указать количество уравнений системы

после нажатия ОК появляется новое окно, в котором вводятся уравнения системы и неизвестные переменные

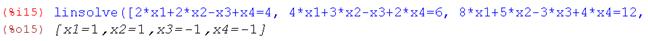
Примеры для самостоятельного решения
Решить системы линейных уравнений AХ = В
1)  ,
,  . 2)
. 2)  ,
,  .
.
3)  ,
, 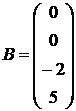 . 4)
. 4)  ,
,  .
.
5)  ,
,  . 6)
. 6)  ,
, 
 .
.
Основы линейной алгебры
Одной из основных задач линейной алгебры является решение систем линейных алгебраических уравнений. К таким системам сводятся многие задачи математического моделирования физических и технологических процессов при их дискретизации, т.е. представления соответствующих дифференциальных уравнений через конечные разности или конечные элементы. Используя алгебру матриц, система линейных алгебраических уравнений представляется в наиболее простой и компактной форме
|
|
А X = B, (2.1)
где А – матрица коэффициентов системы уравнений (основная матрица), X – матрица-столбец неизвестных, В – матрица-столбец свободных членов. Поэтому удобно проводить исследование решений системы (2.1), используя язык матриц. Рассмотрим элементы алгебры матриц.
Понятие матрицы
Определение 2.1. Матрицей называется прямоугольная таблица из n × m чисел, которая содержит m строк и n столбцов.
Обозначения:  или
или  . (2.2)
. (2.2)
Либо кратко [ а ij ] (i = 1,2,…, n; j = 1,2,..,m). В этом случае имеется в виду, что матрица имеет размерность n × m. Матрицы обозначают заглавными латинскими буквами А, В, С, Е,... Числа aij называются элементами матрицы, где первый индекс i означает номер строки, а второй j - номер столбца.
Если в квадратной матрице все элементы главной диагонали равны единице, а все остальные равны нулю, то её называют единичной матрицей. Она обозначается буквой Е и имеет вид
 . (2.3)
. (2.3)
Определение 2.2. Две матрицы А и В называются равными, если они имеют одинаковое количество строк и столбцов и соответствующие элементы которых совпадают.
Матрица, в которой все элементы равны нулю, называется нуль-матрицей или нулевой. Её обозначают буквой О.
Если матрица состоит только из одной строки, то она называется матрицей-строкой. Матрица, состоящая из одного столбца называется матрицей-столбцом.
Если в матрице А поменять строки на столбцы, а столбцы – на соот-ветствующие строки, то полученную матрицу называют транспонированной и обозначают АT.
Действия над матрицами
Сложение.
Операция сложения матриц вводится только для матриц одинаковых размеров.
Определение 2.3. Суммой двух матриц  и
и  называется матрица
называется матрица  такая, что
такая, что  .
.
Пример
 +
+  =
=  .
.
Аналогично определяется разность матриц.
Умножение на число
Определение 2.4. Произведеним матрицы  на число k называется матрица
на число k называется матрица  такая, что
такая, что 
Пример
А =  , k = 2, A∙k =
, k = 2, A∙k = 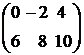 .
.
Разность матриц А – В можно определить так: А – В = А +(– В).
Операции сложения и умножения матрицы на число обладают следующими свойствами:
1. А + В = В + А; 5. 1 ∙ А =А;
2. А + (В + С) = (А + В) + С; 6. α ∙ (А + В)= α ∙А + α ∙В;
3. А + О = А; 7. (α + β)∙А = α ∙А + β ∙А;
4. А – А = О; 8. α ∙ (β ∙ А) = (α ∙ β) ∙ А,
где А, В, С – матрицы, α, β – числа.
Произведение матриц.
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Определение 2.5. Произведением матрицы  на матрицу
на матрицу  называется матрица
называется матрица  такая, что
такая, что
 ,
,
т.е. элемент i-ой строки и k го столбца матрицы произведения С равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы k-го столбца матрицы В.
Получение элемента  схематично изображается так:
схематично изображается так:

Если матрицы А и В квадратные одного размера, то произведение А∙В и В∙А всегда существуют. Легко показать, что А∙Е = Е∙А = А, где А – квадратная матрица, Е – единичная матрица того же размера.
Пример
 ,
,  . Тогда произведение матриц А
. Тогда произведение матриц А  В определяется следующим образом:
В определяется следующим образом:
А  В =
В =  ∙
∙  =
=  =
=  .
.
При этом произведение В  А не определено, так как число столбцов матрицы В (3) не совпадет с числом строк матрицы А (2).
А не определено, так как число столбцов матрицы В (3) не совпадет с числом строк матрицы А (2).
Матрицы А и В называются перестановочными, если АВ = ВА.
Умножение матриц обладает следующими свойствами
1. А ∙ (В ∙ С)= (А ∙ В) ∙ С; 3. (А + В) ∙ С = А∙С + В∙С;
2. А ∙ (В + С) = А∙В + А∙С; 4. α ∙ (А ∙ В)= (α∙ А) ∙ В,
если, конечно, написанные суммы и произведения матриц имеют смысл.
Для операции транспонирования верны свойства:
1. (А+В) Т = АТ + ВТ; 2. (А∙В) Т = АТ ∙ ВТ.
Определители
Любой квадратной матрице А порядка n ставится в соответствие некоторое число, называемое определителем этой матрицы.
Обозначение: det A (или | A | или ΔA).
Определение 2.6. Определителем матрицы 1–го порядка (т.е. матрицы, состоящей из одного элемента, одного числа) называется само число, составляющее заданную матрицу.
Определение 2.7. Определителем матрицы 2-го порядка называется число, полученное с помощью элементов квадратной матрицы 2-го порядка следующим образом:
 .
.
Определение 2.8. Определитель третьего порядка вычисляется по формуле:

При вычислении определителей 3-го порядка удобно пользоваться правилом треугольников, которое символически можно представить так:

Примеры. Вычислить определители третьего порядка
1. 

2. 
Для вычисления определителя матриц 4-го и более высоких порядков рассмотрим дополнительные понятия. Рассмотрим определитель матрицы А n- го порядка
Δn =  .
.
Определение 2.9. Выделим в нём какой-либо элемент aij и вычеркнем i -ю строку и j -й столбец, на пересечении которых расположен этот элемент. Полученный определитель (n-1) –го порядка называется минором Mij элемента aij определителя Δn.
Определение 2.10. Наибольший порядок миноров матрицы А, отличных от нуля, называется рангом матрицы.
Определение 2.11. Алгебраическим дополнением элемента aij определителя Δn называется число
Aij = (-1) i+j Mij.
Определение 2.12. Определителем n-го порядк а Δn вычисляетсясуммой произведения элементов любой строки (столбца)на их алгебраические дополнения
Δn =  =
=  , 1 ≤ i,k ≤ n. (2.4)
, 1 ≤ i,k ≤ n. (2.4)
Пример. Вычислим определитель 4-го порядка  с помощью разложения по 2-му столбцу. Для этого найдем
с помощью разложения по 2-му столбцу. Для этого найдем  и
и 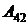 :
:

Следовательно, 
Квадратная матрица А называется невырожденной, если определитель Δ = det A ≠ 0. В противном случае (Δ = 0) матрица А называется вырожденной.
Определение 2.13. Матрица А-1 называется обратной матрице А, если выполняется условие
А А-1 = А-1 А = Е, (2.5)
где Е – единичная матрица того же порядка, что и матрица А. Отметим, что для вырожденной матрицы обратная матрица не существует.
Основные свойства определителей.
1. Определитель, имеющий нулевую строку (столбец), равен нулю.
2. При перестановке двух строк (столбцов) определитель меняет знак.
3. Определитель, имеющий две одинаковы строки (одинаковые столбцы),
равен нулю.
4. Общий множитель любой строки (столбца) можно вынести за знак оп-
ределителя.
5. Если каждый элемент некоторой строки (столбца) определителя Δn представлен в виде суммы двух слагаемых, то этот определитель равен сумме двух определителей. Поясним это на примере определителя 3-го порядка



6. Величина определителя не изменится, если к элементам одной строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число.
7. При транспонировании матрицы её определитель не меняется.
Примеры для самостоятельного решения
Вычислить определители
1)  . 2)
. 2)  . 3)
. 3)  .
.
4)  . 5)
. 5) 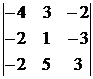 . 6)
. 6)  .
.
Системы линейных алгебраических уравнений (СЛАУ).
Определение 2.14. Системой линейных уравнений (линейной системой ) называется система вида
 (2.6)
(2.6)
где  ,
,  - числа,
- числа,  - неизвестные, n – число неизвестных, m – число уравнений.
- неизвестные, n – число неизвестных, m – число уравнений.
Определение 2.15. Решением линейной системы (2.6) называется набор чисел  которые при подстановке вместо неизвестных обращают каждое уравнение системы в тождество.
которые при подстановке вместо неизвестных обращают каждое уравнение системы в тождество.
Определение 2.16. Если система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной.
Определение 2.17. Система называется определенной, если она имеет только одно решение и неопределенной, если более одного.
Определение 2.18. Для системы линейных уравнений вида (2.6) матрица
А =  называется матрицей системы, а матрица
называется матрицей системы, а матрица
А* =  называется расширенной матрицей системы
называется расширенной матрицей системы
Терема Кронекера – Капелли (критерий совместимости системы)
Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.
Определение 2.19. Если b1, b2, …,bm = 0, то система называется однородной. Однородная система всегда совместна.
Матричный метод решения систем линейных уравнений.
Пусть дана система уравнений: (2.6)
Составим матрицы: A =  ; B =
; B =  ; X =
; X =  .
.
Тогда систему уравнений (2.6) можно записать в матричной форме:
A×X = B. (2.7)
Рассмотрим частный случай системы (2.6), когда число уравнений равно числу неизвестных, т.е. m = n. Пусть квадратная матрица А является невырожденной, т.е. существует обратная матрица А-1. Умножим обе части уравнения (2.7) слева на А-1, получим решение системы (2.6, m = n) в матричной форме
X = A-1 B. (2.8)
Для применения данного метода необходимо находить обратную матрицу, что может быть связано с вычислительными трудностями при решении систем высокого порядка.
Метод Крамера.
Другой метод решения системы линейных алгебраических уравнений основан на теореме Крамера.
Система из n уравнений с n неизвестными
 (2.9)
(2.9)
в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:
xi = Di/D, (2.10)
где D = det A, а Di – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов bi.
Di =  .
.
Формулы вычисления неизвестных (2.8) носят название формул Крамера. Таким образом, правило Крамера позволяет найти единственное решение системы (2.3) или сделать вывод о существовании бесконечного числа решений либо об их отсутствии:
1) Если 
 система (2.3) имеет единственное решение, определяемое по формулам:
система (2.3) имеет единственное решение, определяемое по формулам:  .
.
2) Если  =
=  = 0, система имеет бесконечно много решений.
= 0, система имеет бесконечно много решений.
3) Если  = 0, а хотя бы один из
= 0, а хотя бы один из 
 система не имеет решений.
система не имеет решений.
Если система однородна, т.е. bi = 0, то при D¹0 система имеет единственное нулевое решение x1 = x2 = … = xn = 0.
Пример. Найти решение системы уравнений: 
D =  = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
D1 =  = (28 – 48) – (42 – 32) = -20 – 10 = -30. x1 = D1/D = 1;
= (28 – 48) – (42 – 32) = -20 – 10 = -30. x1 = D1/D = 1;
D2 =  = 5(28 – 48) – (16 – 56) = -100 + 40 = -60. x2 = D2/D = 2;
= 5(28 – 48) – (16 – 56) = -100 + 40 = -60. x2 = D2/D = 2;
D3 =  = 5(32 – 42) + (16 – 56) = -50 – 40 = -90. x3 = D3/D = 3.
= 5(32 – 42) + (16 – 56) = -50 – 40 = -90. x3 = D3/D = 3.
Метод Гаусса
В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.
Рассмотрим систему линейных уравнений:

Разделим обе части 1–го уравнения на a11 ¹ 0, затем:
1) умножим на а21 и вычтем из второго уравнения
2) умножим на а31 и вычтем из третьего уравнения
и т.д.
 , где d1j = a1j/a11, j = 2, 3, …, n+1.
, где d1j = a1j/a11, j = 2, 3, …, n+1.
dij = aij – ai1d1j i = 2, 3, …, n; j = 2, 3, …, n+1.
Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.
Пример. Решить систему линейных уравнений методом Гаусса.

Составим расширенную матрицу системы.
А* = 
Таким образом, исходная система может быть представлена в виде:
 , откуда получаем: x3 = 2; x2 = 5; x1 = 1.
, откуда получаем: x3 = 2; x2 = 5; x1 = 1.
Примеры для самостоятельного решения
Решить системы линейных уравнений двумя способами: методом Крамера и методом Гаусса.
1)  . 2)
. 2)  . 3)
. 3)  .
.
4)  . 5)
. 5) 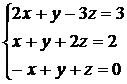 . 6)
. 6)  .
.
|
|
|

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Своеобразие русской архитектуры: Основной материал – дерево – быстрота постройки, но недолговечность и необходимость деления...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!