1. Если игра имеет седловую точку, то решение ее лежит в области чистых стратегий: оптимальной будет максиминная и минимаксная стратегии, а ценой игры - седловой элемент платежной матрицы.
2. Определение оптимальных смешанных стратегий для игр без седловых точек предусматривает решение систем m + n линейных неравенств.




И при условии неотрицательности всех неизвестных pi и qj и при условии, что  pi =1 и
pi =1 и  qj =1
qj =1
Недостаток этого способа - большой объем вычислений.
3. Решение любой конечной матричной игры может быть сведено к решению двух взаимных двойственных задач линейного программирования.
Замечание:
а) исключение доминируемых стратегий может привести к потере некоторых решений;
б) исключение только строго доминируемых стратегий не изменит решения.
Решение матричной игры сведем к задаче линейного программирования.
Рассмотрим случай, когда в платежной матрице (aij)m*n, α≠β и все элементы aij≥0 (это всегда можно получить).
α – нижняя чистая цена игры (максимин)
β – верхняя чистая цена игры (минимакс)
Тогда цена игры v>0 (все элементы матрицы положительны).
Найдем оптимальную смешанную стратегию 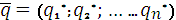 игрока В. Игрок В проигрывает не более v при любой чистой стратегии Аi игрока А, т.е.
игрока В. Игрок В проигрывает не более v при любой чистой стратегии Аi игрока А, т.е. 
 Разделим обе части неравенства на V:
Разделим обе части неравенства на V:  aij(qj / V
aij(qj / V  1), (i=
1), (i=  ) Обозначив qj / V=yj (j=
) Обозначив qj / V=yj (j= 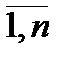 ), получим
), получим  aij yj ≤1 (i=
aij yj ≤1 (i=  ) все yj ≥0 (j=
) все yj ≥0 (j= 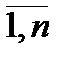 )Кроме того, yj – удовлетворяют условию.
)Кроме того, yj – удовлетворяют условию.
 yj =
yj =  (qj / V) = (1/ V)
(qj / V) = (1/ V)  qj =1/ V
qj =1/ V
Игрок В стремится сделать свой гарантированный проигрыш V возможно меньше, а значит возможно большей величину
1/ V=  yj =
yj = 
Тогда задача линейного программирования будет формулироваться следующим образом.
Найти оптимальный вектор  , который
, который
удовлетворял бы системе линейных ограничений:

yj ≥0 (j= 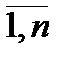 ) и обращал бы линейную функцию
) и обращал бы линейную функцию
 =
=  в максимум.
в максимум.
Найдя  max, определим цену игры и компоненты оптимальной стратегии игрока В.
max, определим цену игры и компоненты оптимальной стратегии игрока В.
V=1/  max; qj*=(1/ V) yj* (j=
max; qj*=(1/ V) yj* (j= 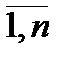 )
)
Рассуждая аналогичным образом на стороне игрока А придем к задаче:
Найти оптимальный вектор  *=(x1*,x2*,…,xm*) удовлетворяющий системе линейных ограничений
*=(x1*,x2*,…,xm*) удовлетворяющий системе линейных ограничений
 aijxi ≥1, (j=
aijxi ≥1, (j= 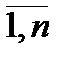 ), xi ≥0 (i=
), xi ≥0 (i=  ) и обращающий линейную функцию f=
) и обращающий линейную функцию f=  в минимум. Найдя fmin, определим цену игры и компоненты оптимальной смешанной стратеги и игрока А. v=1/ fmin;
в минимум. Найдя fmin, определим цену игры и компоненты оптимальной смешанной стратеги и игрока А. v=1/ fmin;  =(1/ V) xi* (i=
=(1/ V) xi* (i=  ).
).
Эти задачи образуют пару симметричных двойственных задач линейного программирования.
Пример решения матричной игры в смешанных стратегиях методом линейного программирования
Найти решение игры с платежной матрицей

Решение. В данной игре α=3, β=4, то есть α≠β, а потому игру следует решать в смешанных стратегиях. Как видно, доминируемых стратегий в матрице нет и все элементы не отрицательны.
Найдем сначала оптимальную смешанную стратегию  игрока В. С этой целью составим задачу линейного программирования, используя платежную матрицу:
игрока В. С этой целью составим задачу линейного программирования, используя платежную матрицу:
 =y1+y2+y3+y4
=y1+y2+y3+y4 
4y1+3y2+4y3+2y4≤1
3y1+4y2+6y3+5y4≤1
2y1+5y2+y3+2y4≤1 yj≥0 (j=  )
)
В канонической форме задача будет иметь вид:
4y1+3y2+4y3+2y4+y5=1
3y1+4y2+6y3+5y4+y6=1
2y1+5y2+y3+2y4+y7=1
yj≥0 (j=  )
)
Переменные y5,y6,y7 составляют начальный базис. Решим задачу симплексным методом.
Первая симплексная таблица будет иметь вид:
| Б.п.
| №1
| y1
| y2
| y3
| y4
| y5
| y6
| y7
| bi
|
| y5
|
|
|
|
|
|
|
|
|
| y6
|
|
|
|
|
|
|
|
|
| y7
|
|
|
|
|
|
|
|
|

| -1
| -1
| -1
| -1
|
|
|
|
|
Находим ведущую строку соответствующую min(1/4; 1/3;1/2) =1/4
Переходим к построению второй симплексной таблицы:
| Б.п.
| №2
| y1
| y2
| y3
| y4
| y5
| y6
| y7
| bi
|
| y1
|
| 3/4
|
| 1/2
| 1/4
|
|
| 1/4
|
| y6
|
| 7/4
|
| 7/2
| -3/4
|
|
| 1/4
|
| y7
|
| 7/2
| -1
|
| -1/2
|
|
| 1/2
|

|
| -1/4
|
| -1/2
| 1/4
|
|
| 1/4
|
Находим ведущую строку соответствующую min(1/2; 1/14;1/4) =1/14
Переходим к построению третьей симплексной таблицы:
| Б.п.
| №3
| y1
| y2
| y3
| y4
| y5
| y6
| y7
| bi
|
| y1
|
| 1/2
| 4/7
|
| 5/14
| -1/7
|
| 3/14
|
| y4
|
| 1/2
| 6/7
|
| -3/14
| 2/7
|
| 1/14
|
| y7
|
| 5/2
| -19/7
|
| -1/14
| -4/7
|
| 5/14
|

|
|
| 3/7
|
| 1/7
| 1/7
|
| 2/7
|
Получим оптимальный план
Y1=3/14; y2=0; y3=0; y4=1/14,  max =2/7; qj=yj V, где V=3,5
max =2/7; qj=yj V, где V=3,5
Отсюда имеем: Цена игры v= (находится между α=3 и β=4), qj*=(3/4;0;0;1/4)
План решения двойственной задачи х1=1/7; х2=1/7;х3=0;
fmin =2/7;pi=xi/v
Отсюда для игрока А цена игры v=1/ fmin =3,5, а оптимальный план игры рi *=(1\2;1\2;0)
Вывод: Игрок А должен использовать стратегию А1и А2 с вероятностью 1/2, а стратегию А3 не применять. Игрок В – должен использовать стратегию В1 с вероятностью 3/4 и стратегию В4 с вероятностью 1/4, стратегии В2 и В3 не применять. Цена игры составляет 3,5 ден.ед.
Пример решение матричной игры в смешанных стратегиях с помощью персонального компьютера (ПК)
Рассмотрим задачу линейного программирования, сформулированную в п. 6 настоящей работы.
Система ограничений: 4y1+3y2+4y3+2y4≤1
3y1+4y2+6y3+5y4≤1
2y1+5y2+y3+3y4≤1
yj≥0 (j=  )
)
Функция цели:  =y1+y2+y3+y4
=y1+y2+y3+y4 
Войдя в MS EXCEL, создадим форму для ввода условий задачи. Для сформулированной задачи форма будет иметь вид:
|
| A
| B
| C
| D
| E
| F
| G
| H
|
|
|
| Переменные
|
|
|
|
|
| Имя
| Y1
| Y2
| Y3
| Y4
|
|
|
|
|
| Зн-ие
|
|
|
|
|
|
|
|
|
| Ниж.гр.
|
|
|
|
|
|
|
|
|
| Вер. гр.
|
|
|
|
|
|
|
|
|
| Ф.Ц.
|
|
|
|
| max
|
|
|
|
| Ограничения
|
|
| Вид
|
|
|
|
| Л. Ч.
| Знак
| Пр. Ч.
|
|
| Огр. 1
|
|
|
|
|
|
|
|
|
| Огр. 2
|
|
|
|
|
|
|
|
|
| Огр. 3
|
|
|
|
|
|
|
|
Введенный текст является комментарием и на решение задачи не влияет. Введем исходные данные.
-Коэффициенты функции цели: 1 в B6; 1 в C6; 1 в D6; 1 в E6;
-Коэффициенты при неизвестных и свободные члены в системе ограничений построчно: 4 в B9; 3 в C9; 4 в D9; 2 в E9;
3 в B10; 4 в C10; 6 в D10; 5 в E10;
2 в B11; 5 в C11; 1 в D11; 3в E11;
-Знак неравенства ≤ в G9; G10; G11.
В результате получим:
|
| A
| B
| C
| D
| E
| F
| G
| H
|
|
|
| Переменные
|
|
|
|
|
| Имя
| Y1
| Y2
| Y3
| Y4
|
|
|
|
|
| Зн-ие
|
|
|
|
|
|
|
|
|
| Ниж.гр.
|
|
|
|
|
|
|
|
|
| Вер. гр.
|
|
|
|
|
|
|
|
|
| Ф.Ц.
|
|
|
|
|
|
|
|
|
| Ограничения
|
|
| Вид
|
|
|
|
| Л. Ч.
| Знак
| Пр. Ч.
|
|
| Огр. 1
|
|
|
|
|
| ≤
|
|
|
| Огр. 2
|
|
|
|
|
| ≤
|
|
|
| Огр. 3
|
|
|
|
|
| ≤
|
|
Введем зависимость для целевой функции. Установим курсор в F6. Курсор на кнопку Мастер функций. Один щелчок по левой кнопке мыши (M1). На экране появится диалоговое окно Мастер функций. Курсор в окно Категория на категорию Математические М1. Курсор в окно на СУММПРОИЗВ. М1.
На экране появится диалоговое окно СУММПРОИЗВ
В массиве 1 следует ввести $В$3:$E$3. Во все диалоговые окна адреса ячеек удобно вводить не с клавиатуры, а протаскивая мышь по ячейкам, чьи адреса следует ввести. В массив 2 введем В6:E6. Курсор на
«Готово» и М 1.
На экране в F6 прочитаем введенное значение целевой функции (=СУММПРОИЗВ ($В$3:$E$3;В6: E6)).
Введем зависимости для левых частей ограничений: курсор в F6; копировать в буфер, курсор в F9; вставка из буфера. На экране в F9 будет введена функция (=СУММПРОИЗВ ($В$3:$E$3;В9:E9)). Затем копируем E9 в E10 и в E11. На этом ввод данных закончен.
Теперь приступаем к поиску решения. Для этого используем функцию Сервис, Поиск решения …. На экране появится окно Поиск решения.
Назначим целевую функцию: курсор в окно «Установить целевую ячейку»; ввести адрес E6; ввести направление целевой функции - максимальное значение.
Для ввода адресов искомых переменных: курсор в поле «Изменяя ячейки»; ввести адреса ВЗ: EЗ; курсор на функцию «Добавить …»; M1.
На экране появится диалоговое окно «Добавить ограничения».
Введем граничные условия на переменные (пер.1 ≥ 0, пер.2 ≥ 0,
пер.3 ≥ 0, пер.4 ≥ 0); ВЗ ≥ В4; СЗ ≥ С4; DЗ ≥ D4; EЗ ≥ E4 (в окне ссылка на ячейку ввести ВЗ: курсор на стрелку; М1; курсор на знак ≥; M1; курсор в правое окно; ввести В4; «Добавить ….». Аналогично вводится граничное условие СЗ ≥ С4; DЗ ≥ D4; EЗ ≥ E4; H9 ≥ F9; H10 ≥ F10; H11 ≥ F11. После ввода последнего ограничения вместо «Добавить …» вводим ОК. На экране появится диалоговое окно «Поиск решения» с введенными условиями.
Если при вводе задачи возникает необходимость в изменении или удалении внесенных ограничений или граничных условий, то это делается с помощью команд «Изменить …», «Удалить …».
С помощью команд, находящихся в окне «Параметры поиска решения», можно вводить условия для решения задач оптимизации всех классов. Команды, используемые по умолчанию, подходят для решения большинства практических задач. В поле «Максимальное время» можно ввести время, не превышающее 32767 с. (более 9 часов). В поле «Предельное число итераций 100» подходит для решения большинства задач. Установление флажка Линейные модели обеспечивает применение симплекс-метода. ОК. На экране появится диалоговое окно «Поиск решения».
Устанавливаем курсор на «Выполнить». M1. После выполнения на экране появится диалоговое окно «Результаты поиска решения». Решение найдено, и результат оптимального решения задачи приводится в таблице, после в Типе отчета опции Результаты. ОК. По умолчанию найденное решение сохраняется.
|
| A
| B
| C
| D
| E
| F
| G
| H
|
|
|
| Переменные
|
|
|
|
|
| Имя
| Y1
| Y2
| Y3
| Y4
|
|
|
|
|
| Зн-ие
| 0,214286
|
|
| 0,071429
|
|
|
|
|
| Ниж.гр.
|
|
|
|
|
|
|
|
|
| Вер. гр.
|
|
|
|
|
|
|
|
|
| Ф.Ц.
|
|
|
|
| 0,285714
|
|
|
|
| Ограничения
|
|
| Вид
|
|
|
|
| Л. Ч.
| Знак
| Пр. Ч.
|
|
| Огр. 1
|
|
|
|
|
| ≤
|
|
|
| Огр. 2
|
|
|
|
|
| ≤
|
|
|
| Огр. 3
|
|
|
|
| 0,642857
| ≤
|
|
Из таблицы видно, что в оптимальном решении Y1=0,214286, Y2= Y3=0, Y4=0,071429. При этом максимальное значение целевой функции будет составлять F6=0,285714. Если условия задачи будут несовместными, решение задачи не будет найдено, о чем будет сообщено.
Анализ оптимального решения выполняется на основании применения положений симплекс-метода, которые были изложены в пп. 3, 5, 6 и начинается после появления диалогового окна Результат поиска решения. С помощью этого диалогового окна можно вызвать отчеты трех типов: результаты, устойчивость, пределы.
Отчет по результатам начинается с установления курсора на результат ОК. На экране вызванный отчет на новом листе, на ярлычке которого указано название отчета M1. На экране высвечивается вызванный отчет.
Microsoft Excel 8.0 Отчет по результатам
| Целевая ячейка (Максимум)
|
|
|
|
|
|
| Ячейка
| Имя
| Исходное значение
| Результат
|
|
|
|
|
| $F$6
| Ф.Ц.
|
| 0.285714286
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Изменяемые ячейки
|
|
|
|
|
|
|
| Ячейка
| Имя
| Исходное значение
| Результат
|
|
|
|
|
| $B$3
| Зн-е У1
|
| 0.214285714
|
|
|
|
|
| $C$3
| Зн-е У2
|
|
|
|
|
|
|
| $D$3
| Зн-е У3
|
|
|
|
|
|
|
| $E$3
| Зн-е У4
|
| 0.071428571
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Ограничения
|
|
|
|
|
|
|
| Ячейка
| Имя
| Значение
| Формула
| Статус
| Разница
|
|
|
| $H$9
| <= Пр.Ч.
|
| $H$9>=$F$9
| связанное
|
|
|
|
| $H$10
| <= Пр.Ч.
|
| $H$10>=$F$10
| связанное
|
|
|
|
| $H$11
| <= Пр.Ч.
|
| $H$11>=$F$11
| не связан.
| 0.357142857
|
|
|
| $B$3
| Зн-е У1
| 0.214285714
| $B$3>=0
| не связан.
| 0.214285714
|
|
|
| $C$3
| Зн-е У2
|
| $C$3>=0
| связанное
|
|
|
|
| $D$3
| Зн-е У3
|
| $D$3>=0
| связанное
|
|
|
|
| $E$3
| Зн-е У4
| 0.071428571
| $E$3>=0
| не связан.
| 0.071428571
|
|
|
| $B$3
| Зн-е У1
| 0.214285714
| $B$3>=$B$4
| не связан.
| 0.214285714
|
|
|
| $C$3
| Зн-е У2
|
| $C$3>=$C$4
| связанное
|
|
|
|
| $D$3
| Зн-е У3
|
| $D$3>=$D$4
| связанное
|
|
|
|
| $E$3
| Зн-е У4
| 0.071428571
| $E$3>=$E$4
| не связан.
| 0.071428571
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отчет состоит из трех таблиц:
В таблице 1 приводятся сведения о целевой функции. В столбце Исходно приводятся значения целевой функции до начала вычисления.
В таблице 2 приводится значение искомых переменных, полученных в результате решения задачи.
В таблице 3 приводятся результаты оптимального решения для ограничения и для граничных условий.
Для ограничений в графе Формула приводятся зависимости, которые были введены в диалоговое окно Поиск решения. В графе Значение приведены величины использованного ресурса. В графе Разница показано количество неиспользованного ресурса. Если ресурс использован полностью, то в графе Состояние указывается: Связанное; при неполном использовании ресурса в этой графе указывается: Не связанное. Для граничных условий приводятся аналогичные величины, с той лишь разницей, что вместо величины неиспользованного ресурса показана разность между значением переменной в найденном оптимальном решении и заданным для нее граничным условием.
Microsoft Excel 8.0 Отчет по устойчивости
| Изменяемые ячейки
|
|
|
|
|
|
|
|
|
|
| | | Результ.
| Нормир.
| Целевой
| Допустимое
| Допустимое
|
|
|
|
|
| Ячейка
| Имя
| значение
| стоимость
| Коэффициент
| Увеличение
| Уменьшение
|
|
|
|
|
| $B$3
| Зн-е У1
| 0.214285714
|
|
|
|
|
|
|
|
|
| $C$3
| Зн-е У2
|
|
|
|
| 1E+30
|
|
|
|
|
| $D$3
| Зн-е У3
|
| -0.428571429
|
| 0.428571429
| 1E+30
|
|
|
|
|
| $E$3
| Зн-е У4
| 0.071428571
|
|
| 0.666666667
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Ограничения
|
|
|
|
|
|
|
|
|
|
| | | Результ.
| Теневая
| Ограничение
| Допустимое
| Допустимое
|
|
|
|
|
| Ячейка
| Имя
| значение
| Цена
| Правая часть
| Увеличение
| Уменьшение
|
|
|
|
|
| $F$9
| Огр.1 Л.Ч.
|
| 0.142857143
|
| 0.333333333
| 0.6
|
|
|
|
|
| $F$10
| Огр.2 Л.Ч.
|
| 0.142857143
|
| 0.625
| 0.25
|
|
|
|
|
| $F$11
| Огр.3 Л.Ч.
| 0.642857143
|
|
| 1E+30
| 0.357142857
|
|
|
|
Отчет по устойчивости состоит из двух таблиц. В таблице 1 приводятся следующие значения для переменных:
w результат решения задачи;
w редуцированная стоимость, т. е. дополнительные двойственные переменные, которые показывают, насколько изменится целевая функция при принудительном включении единицы этой продукции в оптимальное решение;
w коэффициенты целевой функции;
w предельные значения приращения коэффициентов целевой функции, при которых сохраняется набор переменных, входящих в оптимальное решение.
В таблице 2 приводятся аналогичные значения для ограничений:
w величина использованных ресурсов;
w теневая цена, т. е. двойственные оценки, которые показывают, как изменится целевая функция при изменении ресурсов на единицу;
w значения приращения ресурсов, при которых сохранится оптимальный набор переменных, входящих в оптимальное решение
Microsoft Excel 8.0 Отчет по пределам
|
| | Целевое
| |
|
|
|
|
|
|
|
|
|
| Ячейка
| Имя
| Значение
|
|
|
|
|
|
|
|
|
|
| $F$6
| Ф.Ц.
| 0.285714286
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| | Изменяемое
| |
| Нижний
| Целевой
|
| Верхний
| Целевой
|
|
|
|
| Ячейка
| Имя
| Значение
|
| предел
| результат
|
| предел
| результат
|
|
|
|
| $B$3
| Зн-е У1
| 0.214285714
|
|
| 0.071428571
|
| 0.214285714
| 0.285714286
|
|
|
|
| $C$3
| Зн-е У2
|
|
|
| 0.285714286
|
|
| 0.285714286
|
|
|
|
| $D$3
| Зн-е У3
|
|
|
| 0.285714286
|
|
| 0.285714286
|
|
|
|
| $E$3
| Зн-е У4
| 0.071428571
|
|
| 0.214285714
|
| 0.071428571
| 0.285714286
|
|
|
В отчете по пределам показано, в каких пределах может изменяться переменная, вошедший в оптимальное решение:
w приводятся значения в оптимальном решении;
w приводятся нижние пределы изменения значений.







 pi =1 и
pi =1 и  qj =1
qj =1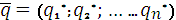 игрока В. Игрок В проигрывает не более v при любой чистой стратегии Аi игрока А, т.е.
игрока В. Игрок В проигрывает не более v при любой чистой стратегии Аi игрока А, т.е. 
 1), (i=
1), (i=  ) Обозначив qj / V=yj (j=
) Обозначив qj / V=yj (j= 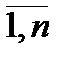 ), получим
), получим 
 , который
, который
 в максимум.
в максимум. *=(x1*,x2*,…,xm*) удовлетворяющий системе линейных ограничений
*=(x1*,x2*,…,xm*) удовлетворяющий системе линейных ограничений в минимум. Найдя fmin, определим цену игры и компоненты оптимальной смешанной стратеги и игрока А. v=1/ fmin;
в минимум. Найдя fmin, определим цену игры и компоненты оптимальной смешанной стратеги и игрока А. v=1/ fmin;  =(1/ V) xi* (i=
=(1/ V) xi* (i= 
 игрока В. С этой целью составим задачу линейного программирования, используя платежную матрицу:
игрока В. С этой целью составим задачу линейного программирования, используя платежную матрицу: =y1+y2+y3+y4
=y1+y2+y3+y4 
 )
) )
)


