Обоснование статистических решений.

Сравнение методов Байеса и минимакса.

Цель работы:

1. Практическое применение методов обоснования статистических решений.

2. Сравнение методов Байеса и Минимакса.

Описание методов:

1. Метод Байеса: состоит в минимизации осредненного (Байесовского) риска.

Существует 2 возможных состояния:

w₁ - объект работоспособен; вероятность - р_1;

w₂ - объект не работоспособен; вероятность – р_2;

Р₁ и Р₂ известны нам, еще до проведения испытаний;

Признаком возможных состояний является некая измеренная на опыте случайная величина-X;

Р₁₂ - вероятность совершить ошибку 1-го рода;

С₁₂ - плата за эту ошибку;

Р₂₁ - вероятность совершить ошибку 2-го рода;

С₂₁ - цена ошибки 2 - го рода;

R - средний риск;

R = C₁₁P₁P₁₁ + C₁₂P₁P₁₂ + C₂₁P₂P₂₁ + C₂₂P₂P₂₂

R min- байесовский риск.

f (X_O/d₁) / f (X_O/d₂ ) = (C₂₂ - C₂₁) P₂ / (C₁₁ - C₁₂) P₁ =

Если по итогам испытаний будет получено такое значение признака, то есть величина х, при котором отношение f (x/d₁) / f (x/d₂) 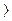, то X X_O и нужно принимать решение d₁, а иначе - d₂.

2. Минимаксный принцип: состоит в минимизации максимального риска.

Состояния w₁ и w₂,

решения d₁ и d₂;

f (x/d₁), f (x/d₂) - заданы

C₁₁=C₂₂=0; C₁₂, C₂₁ - заданы.

P₁ и P₂ - неизвестны.

P₂ = 1- P₁

= C₂₁ / C₁₂ P₂ / P₁ = C₂₁ / C₁₂ 1-P₁^* / P₁^*

Если известно, то вступает в действие принцип Байеса

min max R = C₁₂P₁^* )dx + C₂₁ (1-P₁^* ) ⁾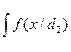

Исходные данные:

результаты измерений содержания железа в масле гидроцилиндра г/т
годный	4,7	3,8	6,2	4,3	6,4	5,5
негодный	12,3	10	13,7	11,1	11,1	9

 

Результаты расчетов:

среднее значение	дисперсия	с.к.о.
5,15	1,107	1,052141
11,2	2,752	1,658915
Зависимость Х0 от значения цены ошибки 2-ого рода.
C21	P1	Минимакс	Байес
1	0,9	7,784	11,306
10	6,231	9,341
50	5,137	7,732
100	4,688	6,949
500	3,817	4,786
1000	3,534	3,597

Зависимость Х0 от значения вероятности Р1.

C21	P1	Минимакс	Байес
20	0,5	5,756	6,226
0,6	5,756	6,731
0,7	5,756	7,25
0,8	5,756	7,846
0,9	5,756	8,678
0,99	5,756	10,825

Выводы:

1. С ростом цены ошибки второго рода решение по методу Байеса приближается к решению по методу минимакса, и оба решения становятся более строгими.
2. С ростом вероятности нахождения изделия в годном состоянии Р1 решение по методу Байеса становится более мягким (разрешает более длительную эксплуатацию изделия). Решение по методу минимакса не зависит от вероятности Р1.
3. В любом случае решение по методу минимакса является более строгим, чем по методу Байеса, то есть применяется тогда, когда риск выше.

 

 

Лабораторная работа № 2.

Проверка статистических гипотез о законах распределения. Определение гарантированной скорости предела сквозного пробития Vпсп методом статистических испытаний.

 

Цель работы: Ознакомление с методом статистических испытаний. Определение вида и параметров закона распределения случайной величины V _псп– скорости сквозного пробития преграды. Определение гарантированной скорости сквозного пробития.

слении характеристик этого процесса.

 

Постановка задачи.

Рассматривается стрельба артиллерийским бронебойным снарядом по бронеплите. В качестве показателя эффективности действия БП-ов используется величина V псп– скорость предела сквозного пробития. Показатель зависит от двух групп факторов (рис.1): конструктивных характеристик БП и их технологических отклонений. Из числа конструктивных характеристик учитываются:

d + Dd - калибр [м];

q + D q - масса [кг];

h гч + D h гч- высота головной части [м];

b + D b - толщина преграды [м];

s т + Ds т- предел текучести материала преграды [Па];

r + Dr - плотность материала преграды [кг/м3];

d т + D d т- диаметр притупления головной части [м].

 

Рекомендуемые примерные отклонения параметров + D:

калибр - до 0.5%;

масса - (2/3)%;

высота головной части - до 5%;

толщина преграды - до 0.5%;

предел текучести мат. преграды - до 3%;

плотность мат. преграды - до 1%;

диаметр притупления головной части до 1%.

500 количество опытов

10 количество pазpядов (выбирается в зависимости от количества опытов);

 

Требуется, используя метод вычислительного эксперимента, рассчитать статистические характеристики распределения значений скорости предела сквозного пробития преграды, установить вид и параметры закона распределения. Сделать выводы по результатам исследования.

 

 

Рис.1 Расчетная схема.

 

Описание метода.

 

Метод исследования: метод статистических испытаний заключается в воспроизведении исследуемого физического процесса при помощи вероятностной математической модели и вычи

Статистической гипотезой (СГ) называется любое предположительное суждение о вероятностных характеристиках случайных величин.

Различают два вида статистических гипотез: о законах распределения и о числовых характеристиках. Например, предположение о том, что исследуемая случайная величина подчиняется нормальному распределению, является статистической гипотезой первого вида.

Любая СГ может быть принята или отклонена только после проверки ее соответствия опытным данным. Сущность проверки заключается в том, чтобы установить, можно ли расхождение между гипотезой и опытными данными (а такое расхождение всегда будет иметь место) отнести на счет случайной погрешности.

Очевидно, что положительный ответ на данный вопрос будет свидетельствовать в пользу выдвинутой гипотезы. В противном случае придется заключить, что гипотеза не согласуется с опытными данными.

Правило, по которому принимается или отклоняется СГ, называется критерием проверки гипотез. Критерии формируются на основе статистик.

Характерной для практики задачей является аппроксимация эмпирических распределений некоторыми теоретическими, свойства которых известны.

 

где соответственно эмпирическое и теоретическое распределения. Из числа непрерывных распределений важную роль играет нормальное распределение, которое является основным для случайных величин, изменяющихся на бесконечном интервале, когда и отражает процессы, происходящие под воздействием большого числа факторов;

Следует, однако, помнить, что нередко одной и той же гипотезе Но, как показывает практика, может удовлетворять несколько теоретических распределений. Принятие гипотезы Но означает лишь то, что выбранное распределение не противоречит опытным данным. Продолжение испытаний может привести к опровержению сделанного заключения, причем для опровержения достаточно небольшого числа противоречащих основной гипотезе результатов (иногда единичного), в то время как для ее подтверждения необходим большой объем испытаний. Тем самым реализуется принцип асимметрии принятия решений.

Вторая особенность заключается в том, что критическая область всегда является правосторонней вследствие специфики применяемых статистических критериев. При этом, поскольку проверка гипотез о законах распределения всегда проводится при сравнительно большом числе опытных данных, то уровень значимости a = 0,1...0,3 до 0,4.

Наконец, выбор статистического критерия, как и выбор класса теоретических распределений не является формализованным и осуществляется на основе оценки свойств выборочной совокупности (прежде всего ее объема) и свойств самих критериев.

Рассмотрим свойства наиболее распространенных статистических критериев. Применительно к гипотезе первого типа, т.е. к гипотезе Но: , такими критериями являются: критерий (Пирсона), критерий l (Колмогорова) и критерий w² (Мазеса - Крамера - Смирнова).

Статистика критерия Пирсона имеет вид:

где i - порядковый номер интервала гистограммы;

k -число интервалов гистограммы,

mi - количество попаданий случайной величины в i -ый интервал,

n - общее число опытов

-эмпирическая вероятность попадания случайной величины в i -ый интервал

pi=Fi(x) - теоретическая вероятность попадания случайной величины в i -ый интервал

Как видно, в качестве меры расхождения между эмпирическим и теоретическим F(x) законами распределения критерий Пирсона использует относительный квадрат отклонений по всем интервалам гистограммы

Критическое значение табулировано и находится по уровню значимости a и числу степеней свободы n=k-i-1, где i - количество связей, определенно числом оценок параметров, вычисленных по данным выборки. Так, для нормального распределения i=2, если оба параметра x и Sx вычислены по результатам испытаний.

Гипотеза Но принимается, если расчетное значение .

Критерий используется при (по крайней мере ). Существенным его недостатком является произвол в разбиении области значений случайной величины на интервалах, что влияет на объективность вывода. Для того, чтобы уменьшить влияние этого недостатка на окончательное решение, целесообразно руководствоваться следующим положением: при слишком большом числе интервалов картина распределения исследования случайной величины искажается случайными зигзагами частот, слишком малочисленных при узких интервалах; при слишком малом числе интервалов сглаживаются и затушевываются характерные особенности распределения. Поэтому необходимы многовариантные расчеты с разным числом интервалов. В общем случае число k зависит от объема выборки n. Приведем некоторые рекомендации по его выбору:

 

n
k

 

Если интервалы одинаковой длины, то для ее определения используют величину размаха выборки R=Xmax-Xmin, где Xmax, Xmin - минимальное и максимальное значения выборки. В этом случае длина интервала определяется формулой:

Границы отделенных интервалов определяются соотношениями:

1-й интервал: xmin-D; xmin-D+d,

2-й интервал: xmin-D+d; xmin-D+2d,

…………………….

j-й интервал: xmin-D+(i-1)d; xmin-D+id,

……………………

k-й интервал: xmin-D+(k-1)d; xmin-D+kd,

где D=0,01d.

После выбора интервалов подсчитывают mi - число наблюдений, попавших в интервал [di], , т.е. в интервал включаются и те наблюдения, которые приходятся на левую границу интервала.

 

Рекомендации по выполнению работы.

Цель работы: Ознакомление с методом статистических испытаний на примере определения гарантированной скорости сквозного пробития бронированной преграды, путем моделирования бронепробития.

Задачи работы:

1. изучить сущность метода статистических испытаний;

2. изучить методы проверки согласия статистического и теоретического законов распределения;

3. изучить стохастическую модель бронепробития;

4. произвести обработку и анализ результатов расчета.

Теоретический материал

 

Метод Монте-Карло: Метод статистических испытаний заключается в воспроизведении исследуемого физического процесса при помощи вероятностной математической модели и вычислении характеристик этого процесса. Таким образом, метод Монте-Карло - это численный метод решения математической задачи при помощи моделирования случайных величин. Метод основан на многократном проведении испытаний построенной модели с последующей статистической обработкой для определения характеристик рассматриваемого процесса в виде статистических оценок его параметров.

Этот метод целесообразно применять при исследовании систем, функционирование которых определяется многими вероятностными параметрами элементарных явлений; когда построение чисто аналитической вероятностной модели такой системы затруднено. Он базируется на использовании случайных чисел - возможных значений некоторой случайной величины с заданным законом распределения.

Стохастическая модель: Все наблюдаемые процессы, характеризующие физические явления, можно классифицировать в общем виде как детерминированные и недетерминированные. К детерминированным относятся процессы, которые могут быть описаны точными математическими соотношениями. Математические модели движения снаряда в канале ствола орудия, в воздухе после вылета из канала ствола, являются детерминированными. Однако в действительности ни один реальный физический процесс нельзя считать строго детерминированным, поскольку всегда существует возможность того, что какое-то непредвиденное событие изменит течение процесса таким образом, что полученные результаты будут носить иной характер, чем предполагалось ранее.

Полной статистической характеристикой случайной величины является закон распределения. Очень важное практическое значение имеет нормальное распределение, которое наиболее часто используется на практике. В данной лабораторной работе будем исходить из того, что полученная нами характеристика распределяется по нормальному закону и, в дальнейшем, постараемся доказать, что это именно так.

Применительно к гипотезе первого типа, т.е. к гипотезе Н₀: M[ (x)] F(x), используются критерий Пирсона, для оценки степени согласованности эмпирического и теоретического распределений

Рассмотрим статистику критерия Пирсона или c²- критерия. Пусть произведено n независимых опытов, в каждом из которых случайная величина Х приняла определенные значения. Результаты опытов сведены в k разрядов и оформлены в виде статистического ряда:

Ji	x1, x2	x2, x3	...	xi, xi+1	...	xk, xk+1
			...		...

 

, ,

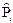
где J_i - i-й интервал (разряд),

k - общее число интервалов,

m_i - число значений в i-м разряде (число измерений величины Х, попавших в i-й разряд).

Величина R= x_max - x_min называется размахом выборки.

Зная F(x), можно найти теоретические вероятности попадания величины Х в каждый из разрядов:

,..., ,..., .

Пусть .

Если , то .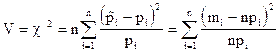

Это и есть статистика Пирсона.

Величина V имеет c²- распределение.

Критическое значение q₂=c²_кр табулировано и находится по уровню значимости a и числу степеней свободы n=k-l-1, где l - количество связей, определяемое числом оценок параметров, вычисленных по данным выборки. Так для нормального распределения l=2, если оба параметра m_x и s_x² рассчитываются по результатам испытаний. В данной задаче число независимых случайных величин равно числу частот 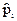, т.е. числу разрядов. Число независимых условий («связей»), накладываемых на частоты 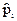, равно 1, если мы требуем, чтобы (это требование накладывается всегда). Число «связей» возрастает до 2, если мы подбираем теоретическое распределение с тем условием, чтобы совпадали теоретические и статистические средние, т.е.

.

Наконец, это число будет равно 3. Если мы потребуем еще совпадения теоретической и статистической дисперсии:

,

где - статистическое среднее на i- м интервале,

- общее статистическое среднее.

Гипотеза Н₀ отклоняется, если c_р²>c_кр².

Критерий Пирсона используется при n 100 ( хотя бы n 50).

Исходные данные для лабораторной работы

Расчет на компьютере

Варианты заданий

		d	q	hгч	b	sigma	ro	dт
	размер	0,014	0,036	0,010	0,015			0,010
	допуск	0,00007	0,0002	0,0005	0,0001			0,0005
	размер	0,018	0,078	0,016	0,018			0,013
	допуск	0,00009	0,0005	0,0008	0,0002			0,0006
	размер	0,023	0,170	0,016	0,023			0,017
	допуск	0,00012	0,0011	0,0008	0,0002			0,0008
	размер	0,027	0,247	0,022	0,027			0,019
	допуск	0,00014	0,0016	0,0011	0,0002			0,0010
	размер	0,030	0,345	0,027	0,031			0,024
	допуск	0,00015	0,0023	0,0013	0,0003			0,0012
	размер	0,045	1,201	0,039	0,046			0,033
	допуск	0,00023	0,0079	0,0020	0,0004			0,0017
	размер	0,057	2,469	0,050	0,061			0,040
	допуск	0,00029	0,0163	0,0025	0,0006			0,0020
	размер	0,076	6,089	0,059	0,076			0,055
	допуск	0,00038	0,0402	0,0029	0,0007			0,0027
	размер	0,085	8,061	0,072	0,091			0,061
	допуск	0,00043	0,0532	0,0036	0,0008			0,0031
	размер	0,100	13,952	0,079	0,109			0,072
	допуск	0,00050	0,0921	0,0039	0,0010			0,0036
	размер	0,115	19,348	0,095	0,104			0,081
	допуск	0,00058	0,1277	0,0048	0,0009			0,0041
	размер	0,122	23,712	0,109	0,123			0,089
	допуск	0,00061	0,1565	0,0054	0,0011			0,0044
	размер	0,130	30,254	0,117	0,125			0,099
	допуск	0,00065	0,1997	0,0058	0,0011			0,0049
	размер	0,152	43,426	0,111	0,138			0,118
	допуск	0,00076	0,2866	0,0055	0,0012			0,0059
	размер	0,180	75,550	0,160	0,193			0,137
	допуск	0,00090	0,4986	0,0080	0,0017			0,0068
	размер	0,203	106,255	0,150	0,216			0,159
	допуск	0,00102	0,7013	0,0075	0,0019			0,0079
	размер	0,305	355,019	0,233	0,330			0,227
	допуск	0,00153	2,3431	0,0117	0,0030			0,0114
	размер	0,037	0,680	0,028	0,039			0,029
	допуск	0,00019	0,0045	0,0014	0,0003			0,0014
	размер	0,045	1,174	0,038	0,041			0,035
	допуск	0,00023	0,0077	0,0019	0,0004			0,0017
	размер	0,105	14,451	0,093	0,101			0,079
	допуск	0,00053	0,0954	0,0047	0,0009			0,0039
	размер	0,125	24,210	0,107	0,131			0,100
	допуск	0,00063	0,1598	0,0053	0,0012			0,0050
	размер	0,023	0,170	0,020	0,024			0,018
	допуск	0,00012	0,0011	0,0010	0,0002			0,0009
	размер	0,085	7,711	0,064	0,082			0,067
	допуск	0,00043	0,0509	0,0032	0,0007			0,0034
	размер	0,076	6,037	0,060	0,080			0,057
	допуск	0,00038	0,0398	0,0030	0,0007			0,0029
	размер	0,057	2,373	0,049	0,063			0,044
	допуск	0,00029	0,0157	0,0024	0,0006			0,0022

 

Пример оформления отчета по лабораторной работе №2

ЛАБОРАТОРНАЯ РАБОТА N 2