

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
Топ:
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует...
Интересное:
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Дисциплины:
|
из
5.00
|
Заказать работу |
Рассмотрим произвольную систему
 (4.1)
(4.1)
когда  .
.
Для нахождения общего метода исследования и решения такой системы введем в рассмотрение ее частный случай. Система вида
 (4.2)
(4.2)
называется системой в базисной форме.
Неизвестные 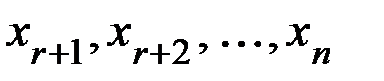 называются свободными, а
называются свободными, а  – несвободными, или базисными, неизвестными. Выбор базисных и свободных переменных может быть различным в общем случае.
– несвободными, или базисными, неизвестными. Выбор базисных и свободных переменных может быть различным в общем случае.
Перенесем все свободные неизвестные в правые части уравнений системы (4.2). Тогда получим
 (4.3)
(4.3)
Если свободным неизвестным  придать конкретные числовые значения, то по формулам (4.3) можно вычислить базисные неизвестные. Таким образом, базисная система (4.2) всегда имеет решение. Причем возможны следующие варианты:
придать конкретные числовые значения, то по формулам (4.3) можно вычислить базисные неизвестные. Таким образом, базисная система (4.2) всегда имеет решение. Причем возможны следующие варианты:
1.  , то есть число уравнений равно числу неизвестных. В этом случае все переменные базисные. Система имеет вид
, то есть число уравнений равно числу неизвестных. В этом случае все переменные базисные. Система имеет вид
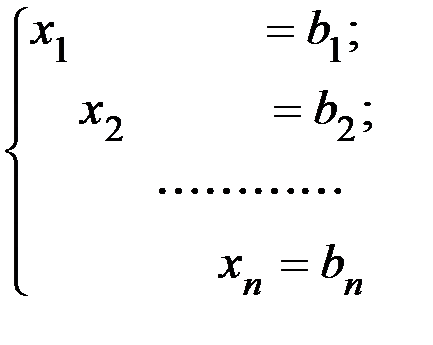
и является определенной, так как имеет единственное, очевидное решение. Матрицей такой системы является единичная матрица
 .
.
2.  . Тогда система с расширенной матрицей вида
. Тогда система с расширенной матрицей вида
 (4.4)
(4.4)
имеет бесконечно много решений, так как при каждом числовом наборе свободных неизвестных базисные неизвестные получают определенные значения по формулам (4.3).
Совокупность 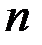 значений неизвестных
значений неизвестных  , связанных соотношениями (4.3), где неизвестные
, связанных соотношениями (4.3), где неизвестные  могут принимать любые числовые значения, называется общим решением системы (4.2) или решением в базисной форме. Частным решением называется всякое решение, полученное из общего при конкретных числовых значениях свободных неизвестных.
могут принимать любые числовые значения, называется общим решением системы (4.2) или решением в базисной форме. Частным решением называется всякое решение, полученное из общего при конкретных числовых значениях свободных неизвестных.
Вывод. Система с базисом всегда совместна. При этом она определенная, если все ее неизвестные базисные, и неопределенная, если кроме базисных неизвестных есть хотя бы одна свободная.
Система (4.1) имеет решение в том и только том случае, когда ее можно записать в базисной форме (4.2), где  .
.
1.5.Метод Гаусса
Рассмотрим теперь общий метод исследования и решения систем вида (4.1), который называется методом Гаусса. Он заключается в том, чтобы преобразовать эту систему к равносильной системе с базисом, для которой вопрос о решениях рассмотрен в предыдущем пункте 1.4.
Метод Гаусса сводится к последовательному исключению неизвестных и основан на применении элементарных преобразований системы, которые приводят к равносильной системе. К элементарным преобразованиям системы уравнений относятся:
1) обмен местами уравнений в системе;
2) умножение уравнения на постоянное число, отличное от нуля;
3) прибавление к уравнению другого уравнения, умноженного предварительно на произвольное число;
4) отбрасывание или добавление уравнения вида  (такое уравнение назовем лишним уравнением).
(такое уравнение назовем лишним уравнением).
Уравнение вида  , где
, где  , назовем противоречивым уравнением. Если в результате элементарных преобразований получилось противоречивое уравнение, то система несовместна.
, назовем противоречивым уравнением. Если в результате элементарных преобразований получилось противоречивое уравнение, то система несовместна.
Для простоты записи вместо всей системы уравнений (4.1) будем записывать только расширенную матрицу коэффициентов, отделяя вертикальной чертой столбец правых частей,
 . (5.1)
. (5.1)
Элементарные преобразования для равносильных систем порождают допустимые преобразования для матриц. Таким образом, в матрице можно:
1) менять местами строки;
2) умножать любую строку на число, отличное от нуля;
3) прибавлять к строке любую другую строку, умноженную на любое число;
4) отбрасывать нулевую строку  , то есть строку коэффициентов лишнего уравнения. Такую строку будем называть лишней.
, то есть строку коэффициентов лишнего уравнения. Такую строку будем называть лишней.
Получение строки вида  , где
, где  , позволяет сделать вывод о несовместности системы. Назовем такую строку противоречивой.
, позволяет сделать вывод о несовместности системы. Назовем такую строку противоречивой.
Универсальный метод Гаусса имеет несколько вычислительных схем. Рассмотрим здесь схему единственного деления. Ее идея заключается в том, чтобы с помощью элементарных преобразований привести матрицу (5.1) к виду
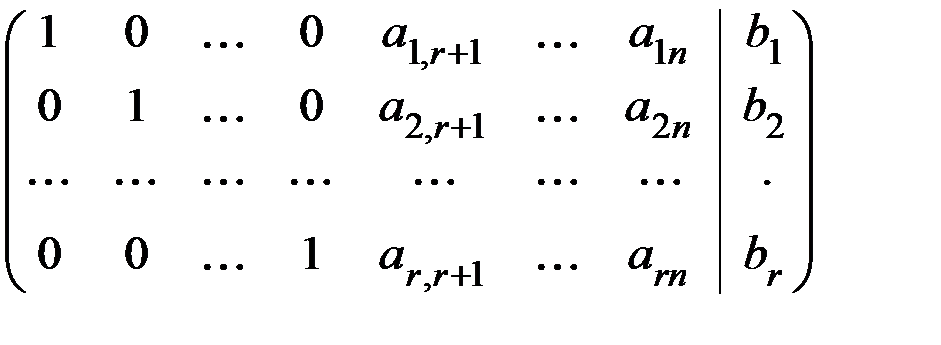 (5.2)
(5.2)
или получить противоречивую строку  , где
, где 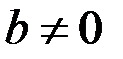 , то есть убедиться в том, что система несовместна. Если противоречий не получено, то система совместная и можно искать ее решения. Метод состоит из двух этапов.
, то есть убедиться в том, что система несовместна. Если противоречий не получено, то система совместная и можно искать ее решения. Метод состоит из двух этапов.
Первый этап – это так называемый «прямой ход». Его цель – преобразовать матрицу к такому виду, когда на главной диагонали стоят 1, а под главной диагональю – 0. Для этого последовательно выполняем следующие шаги.
1-й шаг. Назовем элемент в левом верхнем углу матрицы ведущим, а строку (столбец), содержащую ведущий элемент, ведущей строкой (столбцом). Преобразуем матрицу так, чтобы ведущий элемент равнялся 1. Если в левом столбце есть 1, то меняем местами строки. Если нет, то меняем строки так, чтобы ведущий элемент был отличен от нуля, и делим ведущую строку на ведущий элемент. Получаем матрицу

2-й шаг – «размножение нулей» в ведущем столбце под ведущим элементом, равным 1. Для этого к каждой  -й строке прибавляем ведущую строку, предварительно умноженную на первый элемент
-й строке прибавляем ведущую строку, предварительно умноженную на первый элемент  -й строки, взятый с противоположным знаком. Например, умножаем первую строку на число (
-й строки, взятый с противоположным знаком. Например, умножаем первую строку на число ( ) и складываем со второй строкой. Получаем:
) и складываем со второй строкой. Получаем:
 .
.
Если в ходе этих преобразований получили нулевую строку, то ее следует отбросить. Если получена противоречивая строка, то система решений не имеет. Если противоречий нет, то в результате получим матрицу, в которой, возможно, будет меньше строк, чем в исходной. Она имеет вид
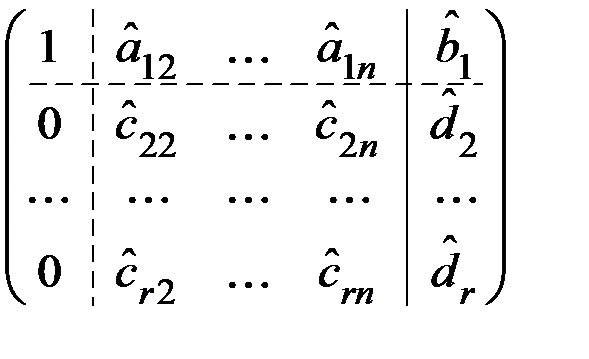 ,
,
где  .
.
3-й шаг. Мысленно отделим строку и столбец, содержащие ведущий элемент. В них «прямой ход» завершен. В оставшейся внутри пунктирных линий матрице снова выделим ведущий элемент и повторим всю процедуру, начиная с 1-го шага.
Если новый ведущий элемент и все элементы под ним – нули, то можно поменять местами столбцы всей матрицы так, чтобы новый ведущий элемент был равен 1 или, по крайней мере, был отличен от нуля. Это всегда можно сделать (иначе ведущая строка либо лишняя, либо противоречивая). Однако это приводит к замене переменных, которую следует обязательно пометить в схеме.
Получаем матрицу
 , (5.3)
, (5.3)
если 
 , или при
, или при 
 . (5.4)
. (5.4)
Второй этап – «обратный ход». На этом этапе размножают нули над главной диагональю матриц (5.3) или (5.4), продвигаясь вдоль нее в обратном направлении: вверх и влево. При этом получается матрица вида (4.4) или единичная матрица. Решение системы с такой матрицей рассмотрено в 1.4.
Несложным оказывается решение систем и с матрицей вида (5.3) или (5.4), которые получаются в результате «прямого хода». Решаем такую систему, начиная с последнего уравнения и подставляя найденные неизвестные в предыдущие уравнения.
Пример 5.1. Решить методом Гаусса систему уравнений
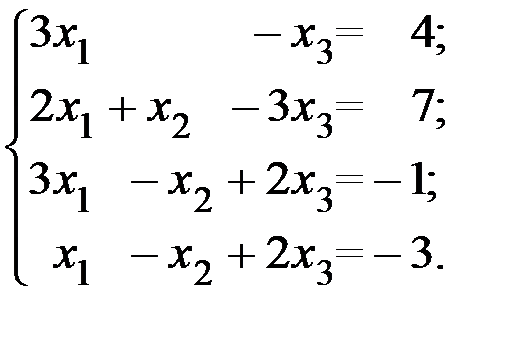
Решение. Выпишем расширенную матрицу коэффициентов заданной системы уравнений и начнем «прямой ход»: переставим четвёртую строку на место первой строки и выделим ведущий элемент.
Первый шаг завершен.
Затем под ведущей единицей размножим нули. Для этого проделаем следующие операции. Умножим первую строку на (–3) и прибавим ко второй строке. Умножим первую строку на (–2) и прибавим к третьей строке. Умножим первую строку на (–3) и прибавим к четвертой строке.
Получим
Второй шаг завершен. Мысленно отбросим первую строку и первый столбец – это третий шаг. В оставшейся внутри пунктирных линий матрице снова начнем с первого шага. Вторую строку поделим на 3. Выделим ведущий элемент.
Размножим нули под ведущей единицей. Для этого умножим вторую строку на (–3) и прибавим к третьей строке. Умножим вторую строку на (–2) и прибавим к четвертой строке.
В полученной матрице отбросим лишнюю нулевую строку. Последнюю строку поделим на 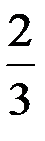 . Получим
. Получим
«Прямой ход» завершен.
«Обратный ход»: полученную расширенную матрицу запишем в виде системы уравнений

Будем решать эту систему, начиная с последнего уравнения. Значение  из последнего уравнения системы подставим во второе уравнение:
из последнего уравнения системы подставим во второе уравнение: 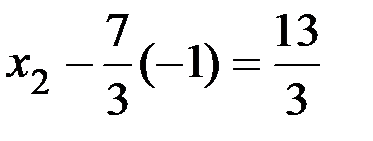 . Получим
. Получим  . Теперь найденные значения переменных
. Теперь найденные значения переменных 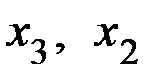 подставим в первое уравнение для нахождения
подставим в первое уравнение для нахождения  . Тогда
. Тогда  и
и  . Найденные значения неизвестных
. Найденные значения неизвестных  подставим в заданную систему уравнений, чтобы убедиться в правильности решения.
подставим в заданную систему уравнений, чтобы убедиться в правильности решения.
Проверка:

Заметим здесь, что жестко фиксированную последовательность шагов, удобную при реализации алгоритма вычисления на компьютере, можно не соблюдать при вычислениях вручную. Например, возможна такая последовательность вычислений:
 .
.
Обратный ход можно также записать в матричной форме. Для этого размножают нули над 1, начиная с нижнего правого угла и перемещаясь вдоль главной диагонали вверх.
 .
.
Вид полученной матрицы позволяет сделать вывод о том, что заданная в этом примере система совместна и определенна.
Ответ: 
Приведем теперь пример несовместной системы.
Пример 5.2. Решить систему 

Решение. Выпишем расширенную матрицу этой системы. В левом верхнем ее углу на месте ведущего элемента стоит 1. Для «размножения нулей» под ведущей 1 умножим первую строку на 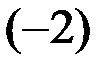 и прибавим ко второй строке. Затем умножим первую строку на
и прибавим ко второй строке. Затем умножим первую строку на  и прибавим к третьей строке. Получим:
и прибавим к третьей строке. Получим:
Размножив нули в первом столбце, мы мысленно отбросили первую строку и первый столбец и продолжили прямой ход в матрице, расположенной внутри пунктирной линии. Вторую строку прибавили к третьей строке. В результате этих преобразований получена противоречивая строка
 ,
,
а следовательно, система несовместна и решения не имеет.
Ответ: нет решения.
Следует отметить, что с помощью схемы Гаусса можно решать одновременно несколько систем с одинаковыми левыми частями и различными правыми. Приведем такой пример.
Пример 5.3: Решить одновременно две системы с одинаковыми левыми частями и различными правыми

Решение. «Прямой ход». Запишем расширенную матрицу коэффициентов, отделив столбцы правых частей каждой системы вертикальной чертой. Поделим первое уравнение на 2. Затем умножим первое уравнение на (–3) и прибавим ко второму уравнению. Умножим первое уравнение на (–4) и прибавим к третьему уравнению. Таким образом

Умножим третью строку на (–1) и поменяем местами со второй строкой. Затем умножим вторую строку на  и прибавим к третьей строке.
и прибавим к третьей строке.
Третью строку поделим на 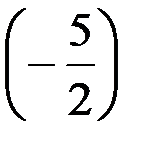 .
.
 .
.
«Прямой ход» завершён.
«Обратный ход»: Решим обе системы, начиная с последнего уравнения и последовательно подставляя найденные значения в предыдущие уравнения.
Решение первой системы: Решение второй системы:

Ответ: 
Проверка:

1.6.Нахождение решения в базисной форме
Схема Гаусса позволяет на первом этапе определить, является ли система совместной. И если система совместна (нет противоречивых строк), то по виду матрицы в конце «прямого хода» можно судить о том, является ли она определенной (квадратная матрица) или неопределенной (число строк меньше, чем число столбцов).
Пример 6.1. Методом Гаусса решить систему


и представить ее решение в базисной форме.
Решение. Выпишем расширенную матрицу системы и выполним первый этап схемы Гаусса – «прямой ход». Умножим первую строку на (–2) и прибавим ко второй строке. Затем вторую строку умножим на (–1).
 .
.
«Прямой ход» завершен. Число строк меньше, чем число столбцов, а значит, система неопределенная и имеет бесконечное множество решений.
«Обратный ход». Выпишем теперь эквивалентную систему с новой матрицей.
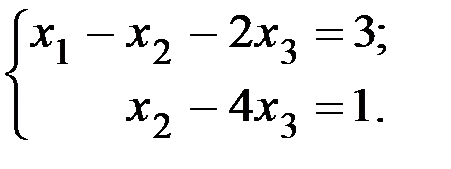
Перенесем слагаемые с переменной  в правую часть равенств. Получим
в правую часть равенств. Получим

Подставляя значение  из последнего уравнения в предыдущее, получим
из последнего уравнения в предыдущее, получим

и
 .
.
Следовательно, решением системы является совокупность

где  – свободная переменная, а
– свободная переменная, а  – базисные переменные.
– базисные переменные.
Ответ: 
Проверка:
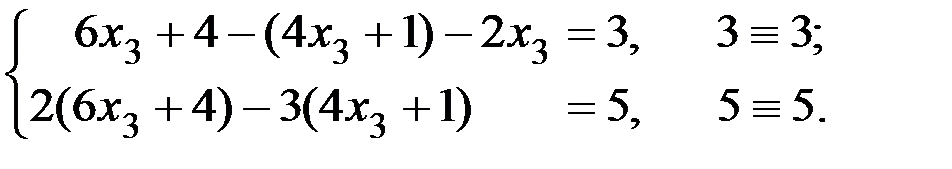
Пример 6.2. Методом Гаусса решить однородную систему

и представить ее решение в базисной форме.
Решение. Для однородной системы столбец свободных членов нулевой, поэтому выписывают не расширенную, а обычную матрицу системы.
«Прямой ход»: умножим первую строку на  и прибавим ко второй строке. Затем вторую строку умножим на
и прибавим ко второй строке. Затем вторую строку умножим на  . Тогда:
. Тогда:
 .
.
«Прямой ход» завершен. «Обратный ход»: перейдем от матрицы к системе

Перенесем переменную  в правую часть каждого уравнения. Получим
в правую часть каждого уравнения. Получим

Подставим значение  из второго уравнения в первое. Тогда
из второго уравнения в первое. Тогда

или

где  – свободная переменная,
– свободная переменная,  – базисные переменные.
– базисные переменные.
Ответ: 
Проверка. Подставим найденное решение в исходную систему. Получим
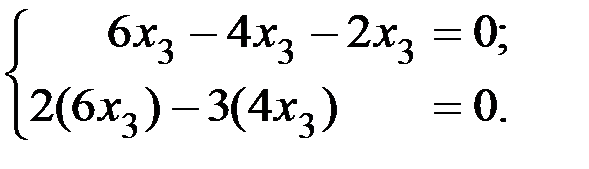
Тогда имеем

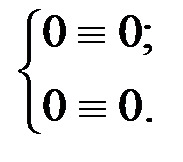

Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!