

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

История создания датчика движения: Первый прибор для обнаружения движения был изобретен немецким физиком Генрихом Герцем...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
Топ:
Установка замедленного коксования: Чем выше температура и ниже давление, тем место разрыва углеродной цепи всё больше смещается к её концу и значительно возрастает...
Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации - обмен информацией между организацией и её внешней средой...
Выпускная квалификационная работа: Основная часть ВКР, как правило, состоит из двух-трех глав, каждая из которых, в свою очередь...
Интересное:
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными...
Дисциплины:
|
из
5.00
|
Заказать работу |
ВВЕДЕНИЕ В ТЕОРИЮ УРАВНЕНИЙ
МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Классификация дифференциальных уравнений
Многие задачи механики и физики могут быть сведены к дифференциальным уравнениям в частных производных. Математическими моделями реальных процессов являются краевые задачи для дифференциальных уравнений при определенных граничных и начальных условиях. При этом оказывается, что одно и то же уравнение может описывать совершенно различные по своей природе явления и процессы. Поэтому при исследовании довольно широкого круга задач механики и физики требуется сравнительно небольшое число различных видов дифференциальных уравнений. Изучением таких уравнений, методами их решения занимается раздел математики «Уравнения математической физики».
В нашем курсе мы будем заниматься уравнениями второго порядка. С помощью этих уравнений можно исследовать в первом приближении основные физические процессы: колебания, теплопроводность, диффузию, течение жидкостей и газа, электростатические явления.
Для решения своих проблем теория «Уравнений математической физики» использует различный математический аппарат: ряды Фурье, интегралы Фурье, интегральные преобразования (Лапласа, Фурье), функции комплексного переменного и др.
Специфическим для уравнений математической физики является то, что здесь постановка задач для уравнений в частных производных делается исходя из физических соображений. Процесс получения решения этих задач основывается на математических методах, но в каждом конкретном случае само решение той или иной задачи должно иметь определенную физическую интерпретацию.
Линейные дифференциальные уравнения
Классификация линейных уравнений и приведение
Их к каноническому виду
Линейные уравнения второго порядка в частных производных делят на три класса, в каждом из которых есть простейшие уравнения, называемые каноническими. Решения уравнений одного и того же класса имеют много общих свойств. Для изучения этих свойств достаточно рассмотреть канонические уравнения, так как другие уравнения данного типа могут быть приведены к каноническому виду.
Запишем линейное относительно производных второго порядка уравнение (1.88) в более краткой форме:
 . .
| (1.92) |
Классификация уравнений вида (1.92) проводится в соответствии со знаком дискриминанта  .
.
Если в некоторой области  выражение
выражение  сохраняет знак, то уравнение (1.92) в этой области принадлежит:
сохраняет знак, то уравнение (1.92) в этой области принадлежит:
а) к гиперболическому типу, если  ;
;
б) параболическому типу, если  ;
;
в) эллиптическому типу, если  .
.
Пример. Определить тип уравнения
 .
.
Решение. Здесь  ,
,  ,
,  и
и  для любых
для любых  и
и  . Значит, на всей плоскости, а следовательно и в некоторой области задания, данное уравнение является уравнением параболического типа.
. Значит, на всей плоскости, а следовательно и в некоторой области задания, данное уравнение является уравнением параболического типа.
Если уравнение рассматривается в области задания  , то указанные три типа не всегда дают исчерпывающую классификацию, так как выражение
, то указанные три типа не всегда дают исчерпывающую классификацию, так как выражение  может не сохранять знак во всей области. Тогда должна существовать кривая
может не сохранять знак во всей области. Тогда должна существовать кривая  , вдоль которой выражение
, вдоль которой выражение  ; эта кривая называется линией параболического вырождения. При этом возможны два случая:
; эта кривая называется линией параболического вырождения. При этом возможны два случая:
1) во всех точках  , кроме
, кроме  ,
,  сохраняет знак, тогда уравнение (1.92) называется уравнением гиперболического или эллиптического типа с линией вырождения
сохраняет знак, тогда уравнение (1.92) называется уравнением гиперболического или эллиптического типа с линией вырождения  ;
;
2) выражение  меняет знак в области
меняет знак в области  , тогда уравнение (1.92) называется уравнением смешанного типа.
, тогда уравнение (1.92) называется уравнением смешанного типа.
Пример. Определить тип уравнения
 .
.
Решение. Здесь  ,
,  ,
,  и, следовательно,
и, следовательно,  . Дискриминант
. Дискриминант  равен нулю, когда
равен нулю, когда  . Значит, гипербола
. Значит, гипербола  является линией параболического вырождения, а данное уравнение относится к смешанному типу, причем области
является линией параболического вырождения, а данное уравнение относится к смешанному типу, причем области  , где
, где 
 , и
, и  , где
, где 
 , являются областями гиперболичности и эллиптичности.
, являются областями гиперболичности и эллиптичности.
Уравнение вида

| (1.93) |
называется каноническим уравнением гиперболического типа.
Второй канонический вид уравнения гиперболического типа таков:
 . .
| (1.94) |
Уравнение вида
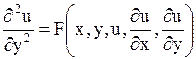
| (1.95) |
называется каноническим уравнением параболического типа.
Уравнение вида

| (1.96) |
называется каноническим уравнением эллиптического типа.
Уравнение (1.92) в каждой из областей, где сохраняется знак дискриминанта  , может быть приведено к уравнению, эквивалентному данному, а именно к каноническому, путем введения вместо
, может быть приведено к уравнению, эквивалентному данному, а именно к каноническому, путем введения вместо  и
и  новых переменных
новых переменных  и
и  с помощью зависимостей
с помощью зависимостей
 , ,  . .
| (1.97) |
При этом от функций  ,
,  требуется, чтобы они были дважды непрерывно дифференцируемыми и чтобы якобиан
требуется, чтобы они были дважды непрерывно дифференцируемыми и чтобы якобиан  , т.е. функциональный определитель
, т.е. функциональный определитель

в рассматриваемой области  . Выражая производные, входящие в уравнение (1.92), по старым переменным через производные по новым переменным, приходят к уравнению
. Выражая производные, входящие в уравнение (1.92), по старым переменным через производные по новым переменным, приходят к уравнению

| (1.98) |
где
 ,
,
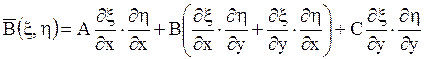 ,
,
 .
.
Непосредственной подстановкой нетрудно проверить, что
 .
.
Из последнего соотношения следует инвариантность типа уравнения при преобразовании переменных, если только якобиан  отличен от нуля.
отличен от нуля.
В преобразовании (1.97) две функции  и
и  можно выбрать так, чтобы выполнялось только одно из условий: 1)
можно выбрать так, чтобы выполнялось только одно из условий: 1)  ,
,
2)  , 3)
, 3) 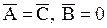 . Другими словами, функции
. Другими словами, функции  и
и  подбираются такими, чтобы в уравнении гиперболического типа исчезли члены с производными
подбираются такими, чтобы в уравнении гиперболического типа исчезли члены с производными  ,
,  , в уравнении параболического типа исчезли члены с производными
, в уравнении параболического типа исчезли члены с производными  ,
,  , в уравнении эллиптического типа -
, в уравнении эллиптического типа -  . Тогда, очевидно, преобразованное уравнение (1.98) примет наиболее простой вид – канонический.
. Тогда, очевидно, преобразованное уравнение (1.98) примет наиболее простой вид – канонический.
Обоснование процедуры канонизации уравнения вида (1.92) мы не приводим; читатель может познакомиться с ним в книгах /1,3/. Здесь же излагается формальная сторона этой процедуры.
Для приведения уравнения (1.92) к каноническому виду надо составить вспомогательное обыкновенное дифференциальное уравнение
 , ,
| (1.99) |
которое называется характеристическим для данного уравнения (1.92).
Характеристическое уравнение (1.99) распадается на два уравнения:
 (или (или  ), ),
| (1.100) |
 (или (или  ). ).
| (1.101) |
Общие интегралы уравнений (1.100) и (1.101)
 и
и 
называют характеристиками данного уравнения (1.92) или характеристическими кривыми. (В связи с этим рассматриваемый метод упрощения уравнения (1.92) называют методом характеристик).
Через каждую точку области  , где уравнение имеет один и тот же тип, проходят две характеристики, причем для уравнений гиперболического типа характеристики действительны и различны, для уравнений эллиптического типа – комплексны и различны, а для уравнений параболического типа обе характеристики действительны и совпадают.
, где уравнение имеет один и тот же тип, проходят две характеристики, причем для уравнений гиперболического типа характеристики действительны и различны, для уравнений эллиптического типа – комплексны и различны, а для уравнений параболического типа обе характеристики действительны и совпадают.
Разберем каждый из этих случаев в отдельности.
СЛУЧАЙ 1. Для уравнений гиперболического типа  и правые части уравнений (1.100) и (1.101) действительны и различны. Общие интегралы их
и правые части уравнений (1.100) и (1.101) действительны и различны. Общие интегралы их  и
и  определяют два различных семейства действительных кривых – характеристик уравнения (1.92).
определяют два различных семейства действительных кривых – характеристик уравнения (1.92).
В этом случае, как установлено, для приведения уравнения (1.92) к каноническому виду следует сделать замену переменных, положив
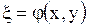 ,
, 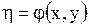 ,
,
в результате чего исходное уравнение преобразуется в уравнение вида
 .
.
Таким образом, получается каноническая форма уравнения гиперболического типа.
Отметим, что с помощью дополнительной замены (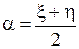 ,
, 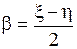 , где
, где 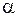 и
и  - новые переменные) уравнение (1.92) может быть приведено к другой канонической форме:
- новые переменные) уравнение (1.92) может быть приведено к другой канонической форме:
 .
.
СЛУЧАЙ 2. Для уравнений параболического типа  , поэтому уравнения (1.100), (1.101) совпадают и результатом их решения является один действительный интеграл
, поэтому уравнения (1.100), (1.101) совпадают и результатом их решения является один действительный интеграл  .
.
В этом случае для приведения уравнения (1.92) к каноническому виду в качестве одной из переменной, например,  , берут
, берут
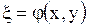 ,
,
другая же переменная выбирается произвольно:

(например,  ), лишь бы только якобиан
), лишь бы только якобиан
 .
.
При таком выборе новых переменных  и
и  уравнение (1.92) принимает канонический вид:
уравнение (1.92) принимает канонический вид:
 .
.
СЛУЧАЙ 3. Для уравнений эллиптического типа  . В этом случае правые части уравнений (1.100) и (1.101) комплексны, а интегралы их будут комплексно-сопряженные. Они определяют два семейства мнимых характеристик.
. В этом случае правые части уравнений (1.100) и (1.101) комплексны, а интегралы их будут комплексно-сопряженные. Они определяют два семейства мнимых характеристик.
Пусть общий интеграл уравнения (1.100) имеет вид
 ,
,
где  - функция, принимающая комплексные значения, а функции
- функция, принимающая комплексные значения, а функции  и
и  - действительные функции действительных переменных. Другой общий интеграл (уравнения (1.101) будет комплексно - сопряженным с указанным.
- действительные функции действительных переменных. Другой общий интеграл (уравнения (1.101) будет комплексно - сопряженным с указанным.
Если положить
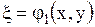 ,
, 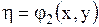 ,
,
то уравнение (1.92) принимает канонический вид:
 .
.
Примечание. После выбора новых переменных  и
и  требуется преобразовать производные, входящие в данное уравнение, к новым переменным. Напомним, что первые производные по старым переменным
требуется преобразовать производные, входящие в данное уравнение, к новым переменным. Напомним, что первые производные по старым переменным  и
и  выражаются через производные по новым переменным
выражаются через производные по новым переменным  и
и  по известным формулам дифференцирования сложной функции:
по известным формулам дифференцирования сложной функции:
 ,
,  .
.
Вторые производные находятся путем дифференцирования выражений для  и
и  , так как
, так как
 ,
,  ,
,  ;
;
при этом при отыскании 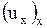 ,
, 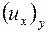 ,
,  опять применяется правило дифференцирования сложной функции.
опять применяется правило дифференцирования сложной функции.
Пример. Привести к каноническому виду уравнение
 .
.
Решение. Здесь  ,
,  ,
,  и
и  . Значит данное уравнение является уравнением параболического типа всюду.
. Значит данное уравнение является уравнением параболического типа всюду.
Составим характеристическое уравнение
 ,
,
которое можно записать в виде
 ,
,
откуда получаем
 .
.
Разделяя переменные в этом уравнении  , после интегрирования его найдем
, после интегрирования его найдем
 или
или  .
.
В соответствии с рассмотренным случаем 2 делаем замену переменных следующим образом:
 ,
,  .
.
Так как функция 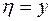 выбиралась произвольно, то надо проверить выполнимость условия
выбиралась произвольно, то надо проверить выполнимость условия
 .
.
Найдем  ,
,  ,
,  ,
,  .
.
Тогда
 .
.
Выразим  ,
,  ,
,  через новые переменные
через новые переменные  и
и  .
.
 ;
;

 ;
;
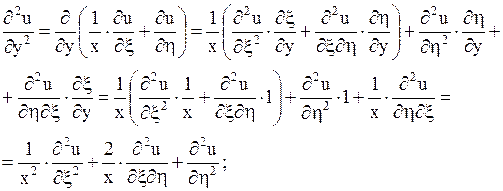

Значения  ,
,  ,
,  подставим в данное уравнение:
подставим в данное уравнение:

откуда получаем
 или
или  .
.
Уравнение теплопроводности
Уравнение вида
 , ,
| (1.106) |
где  - параметр, учитывающий физические свойства изучаемой среды, называется уравнением теплопроводности.
- параметр, учитывающий физические свойства изучаемой среды, называется уравнением теплопроводности.
Оно имеет вид для плоского случая
 , ,
| (1.107) |
для одномерного
 . .
| (1.108) |
Уравнением теплопроводности описываются процессы нестационарного массо- и теплообмена. В частности, к этим уравнениям приводят задачи о неустановившемся режиме распространения тепла (при этом  означает коэффициент температуропроводности, а
означает коэффициент температуропроводности, а  - температуру в любой точке исследуемой области в любой момент времени
- температуру в любой точке исследуемой области в любой момент времени  ); о фильтрации упругой жидкости в упругой пористой среде, например, фильтрация нефти и газа в подземных песчаниках (
); о фильтрации упругой жидкости в упругой пористой среде, например, фильтрация нефти и газа в подземных песчаниках (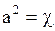 - коэффициент пьезопроводности,
- коэффициент пьезопроводности,  - давление в любой точке среды); о неустановившейся диффузии (
- давление в любой точке среды); о неустановившейся диффузии ( - коэффициент диффузии,
- коэффициент диффузии,  - концентрация); о течении жидкости в магистральных трубопроводах (
- концентрация); о течении жидкости в магистральных трубопроводах ( - давление или скорость жидкости).
- давление или скорость жидкости).
Если при рассмотрении этих задач окажется, что в исследуемой области функционируют внутренние источники и стоки массы или тепла, то процесс описывается неоднородным уравнением
 , ,
| (1.109) |
где функция 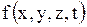 характеризует интенсивность функционирующих источников.
характеризует интенсивность функционирующих источников.
Уравнения (1.106)…(1.109) являются простейшими уравнениями параболического типа.
И ее корректности
Как было показано, уравнения математической физики имеют бесчисленное множество решений, зависящее от двух произвольных функций (речь идет об уравнениях второго порядка для функции двух переменных). Для того, чтобы из множества решений выделить определенное, характеризующее процесс, необходимо на искомую функцию наложить дополнительные условия, которые диктуются физическими соображениями. Тут можно провести аналогию с обыкновенными дифференциальными уравнениями, когда для выделения из общего решения частного, удовлетворяющего некоторым дополнительным условиям, отыскивались по этим условиям произвольные постоянные. Таковыми условиями для уравнений в частных производных являются, чаще всего, начальные и граничные условия. Граничные условия – это условия, заданные на границе рассматриваемой среды; начальные условия – условия, относящиеся к какому-нибудь моменту времени, с которого начинается изучение данного физического явления. Дополнительные условия,
так же как и само дифференциальное уравнение, должны вводиться на основе физических соображений, связанных с самим процессом. Вместе с тем дополнительные условия должны быть такими, чтобы обеспечить выделение из всего множества решений единственного решения. Число граничных и начальных условий определяется типом уравнения, а их вид – заданным исходным состоянием на границе объекта и внешней среды. Для рассматриваемых нами уравнений число начальных условий равно порядку старшей производной по времени, входящей в уравнение, а число граничных условий – порядку старшей производной по координате.
Совокупность дифференциального уравнения и дополнительных условий представляет собой математическую формулировку физической задачи и называется задачей математической физики.
Физическая задача решается по схеме:
1) реальный физический процесс (явление, объект) заменяется некоторым идеальным процессом (явлением, объектом) так, что последний значительно проще первого и вместе с тем сохраняет его основные черты (идеализация процесса);
2) выбирается величина (функция), характеризующая процесс, и используются законы, по которым он происходит;
3) на основании выбранных законов выводится дифференциальное уравнение для величины, характеризующей процесс;
4) выводятся дополнительные условия – начальные и граничные – также в соответствии с выбранными законами.
Итак, задача математической физики состоит в отыскании решений уравнений в частных производных, удовлетворяющих некоторым дополнительным условиям, скажем, граничным и начальным.
Задача математической физики считается поставленной корректно, если решение задачи, удовлетворяющее всем ее условиям, существует, единственно и устойчиво; последнее означает, что малые изменения любого из данных задачи вызывают малое изменение решения. Требование устойчивости необходимо по следующей причине. В данных любой конкретной задачи, особенно если они получены из опыта, всегда содержится некоторая погрешность, и нужно, чтобы малая погрешность в исходных данных приводила к малой неточности в решении. Это требование выражает физическую определенность поставленной задачи.
Примеры
ПРИМЕР 2.36. Выяснить, являются ли приведенные ниже равенства дифференциальными уравнениями в частных производных:
а)  ,
,
б)  .
.
Решение. Преобразуем уравнение а)
 .
.
Данное уравнение является уравнением в частных производных, так как в него входят частные производные второго порядка
 и
и  .
.
Уравнение б) не является уравнением в частных производных, так как в него входит только функция 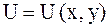 . Действительно, раскрывая
. Действительно, раскрывая  , получим
, получим

ПРИМЕР 2.37. Выяснить, какие из следующих уравнений являются линейными (однородными или неоднородными) и какие нелинейными:
а)  ,
,
б)  ,
,
в) 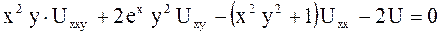 .
.
Решение. Сравнивая данные уравнения с формой (1.4), заключаем, что
- уравнение а) есть неоднородное линейное уравнение второго порядка, для которого 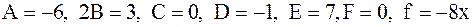 ;
;
- уравнение б) нелинейное, так как оно не является линейным относительно старших частных производных;
- уравнение в) является однородным линейным уравнением третьего порядка.
ПРИМЕР 2.38. Решить уравнение  .
.
Решение. Ясно, что искомая функция  не зависит от переменной
не зависит от переменной  , но может быть любой функцией от
, но может быть любой функцией от  :
:  , поскольку, дифференцируя
, поскольку, дифференцируя  по
по  , получим ноль, а это значит, что данное равенство выполняется. Таким образом, решение уравнения содержит одну произвольную функцию
, получим ноль, а это значит, что данное равенство выполняется. Таким образом, решение уравнения содержит одну произвольную функцию  .
.
ПРИМЕР 2.39. Решить уравнение  , где
, где  заданная функция.
заданная функция.
Решение. Интегрируя по  , восстановим искомую функцию
, восстановим искомую функцию
 , где
, где 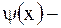 произвольная функция.
произвольная функция.
Итак, решение уравнений в примерах 2.38 и 2.39 содержат одну произвольную функцию  . Такое решение называется общим. В отличие от общего решения обыкновенного дифференциального уравнения первого порядка, которое содержит одну произвольную постоянную, решение уравнения в частных производных первого порядка содержит одну произвольную функцию.
. Такое решение называется общим. В отличие от общего решения обыкновенного дифференциального уравнения первого порядка, которое содержит одну произвольную постоянную, решение уравнения в частных производных первого порядка содержит одну произвольную функцию.
ПРИМЕР 2.40. Решить уравнение  .
.
Решение. Перепишем уравнение так:  . Положим
. Положим  , после чего данное уравнение принимает вид
, после чего данное уравнение принимает вид  . Как было установлено в примере 2.38, общее решение последнего уравнения имеет вид:
. Как было установлено в примере 2.38, общее решение последнего уравнения имеет вид:  , где
, где  произвольная функция. Исходное уравнение примет вид:
произвольная функция. Исходное уравнение примет вид:  . Проинтегрировав полученный результат по
. Проинтегрировав полученный результат по  , получим
, получим
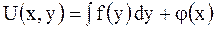 , иначе
, иначе
 ,
,
где  и
и 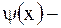 произвольные дважды дифференцируемые функции.
произвольные дважды дифференцируемые функции.
Легко проверить, что найденная функция  удовлетворяет данному уравнению.
удовлетворяет данному уравнению.
Итак, решение уравнения в частных производных второго порядка содержит уже две произвольные функции. Такое решение называют общим.
Приведенные в качестве примеров уравнения дают основание сделать заключение: общее решение уравнения в частных производных первого порядка содержит одну произвольную функцию, а общее решение уравнения второго порядка – две произвольные функции. В этом заключается коренное отличие общего решения уравнения в частных производных от общего решения обыкновенного дифференциального уравнения, которое содержит одну и две произвольные постоянные.
В дальнейшем будет выяснено, какие дополнительные условия надо задать, чтобы с их помощью можно было выделить частное решение, т. е. функцию, удовлетворяющую как уравнению, так и дополнительным условиям.
2.17 КЛАССИФИКАЦИЯ И ПРИВЕДЕНИЕ К КАНОНИЧЕСКОМУ ВИДУ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ
ВТОРОГО ПОРЯДКА
Все многообразие линейных относительно старших производных (или просто линейных) уравнений может быть разделено на три класса (типа). В каждом классе есть простейшие уравнения, которые называются каноническими. Решения уравнения одного и того же типа (класса) имеют много общих свойств. Для изучения этих свойств достаточно рассмотреть канонические уравнения, так как другие уравнения данного класса могут быть приведены к каноническому виду.
Классификация уравнений вида (2.52) проводится в соответствии со знаком дискриминанта 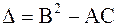 .
.
Говорят, что уравнение (1.3) в области  принадлежит
принадлежит
а) гиперболическому типу, если  ,
,
б) параболическому типу, если 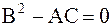 ,
,
в) эллиптическому типу, если  .
.
Уравнение вида

| (2.54) |
называется каноническим уравнением гиперболического типа.
Второй канонический вид уравнения гиперболического типа таков:

| (2.55) |
Уравнение вида

| (2.56) |
называется каноническим уравнением параболического типа.
Уравнение вида

| (2.57) |
называется каноническим уравнением эллиптического типа.
Дифференциальное уравнение

| (2.58) |
называется характеристическим уравнением для уравнения (2.52), а его общие интегралы  и
и  характеристиками.
характеристиками.
Характеристики линейного уравнения (2.52) используются для приведения его к каноническому виду. Уравнение (2.52) в каждой из областей, где сохраняется знак дискриминанта  , приводится к эквивалентному уравнению, а именно к каноническому, путем введения вместо переменных
, приводится к эквивалентному уравнению, а именно к каноническому, путем введения вместо переменных  и
и  новых переменных
новых переменных 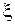 и
и  с помощью зависимостей
с помощью зависимостей
 .
.
Для уравнения гиперболического типа характеристическое уравнение имеет два интеграла, т.е. существуют два семейства действительных характеристик
 и
и  ,
,
и потому следует сделать замену переменных, положив
 ,
,
в результате чего исходное уравнение преобразуется к уравнению (2.54) (или к уравнению (2.55) после дополнительной замены  , где
, где 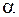 и
и  новые переменные).
новые переменные).
Для уравнения параболического типа характеристическое уравнение имеет один действительный интеграл, т.е. одну характеристику  , и потому полагают
, и потому полагают
 ,
,
где  произвольная функция, например,
произвольная функция, например,  . После такой замены уравнение приводится к виду (2.56).
. После такой замены уравнение приводится к виду (2.56).
Для уравнения эллиптического типа общие интегралы характеристического уравнения имеют вид
 ,
,
где  функция, принимающая комплексные значения, а
функция, принимающая комплексные значения, а  и
и  действительные функции действительных переменных. С помощью подстановок
действительные функции действительных переменных. С помощью подстановок

уравнение (2.52) приводится к каноническому виду (2.57).
После выбора новых переменных 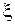 и
и  требуется преобразовать производные, входящие в данное уравнение, к новым переменным. Напомним, что первые производные по старым переменным
требуется преобразовать производные, входящие в данное уравнение, к новым переменным. Напомним, что первые производные по старым переменным  и
и  выражаются через производные по новым переменным
выражаются через производные по новым переменным 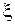 и
и  по известным формулам дифференцирования сложной функции двух переменных:
по известным формулам дифференцирования сложной функции двух переменных:
 .
.
Вторые производные находятся путем дифференцирования выражений для  и
и  по правилу дифференцирования сложной функции.
по правилу дифференцирования сложной функции.
Так как для каждого типа канонических уравнений разработаны определенные методы как аналитического, так и численного решения, то задача приведения уравнений (2.52) к каноническому виду представляет практический интерес.
Заметим, что в различных областях тип одного и того же уравнения (2.52) может быть различным.
Примеры решения задач
ПРИМЕР 2.41. Определить тип уравнения

и привести его к каноническому виду.
Решение. Составим выражение  . В данном случае
. В данном случае  ,
,  , тогда
, тогда 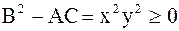 . Отсюда следует, что данное уравнение – уравнение гиперболического типа во всех точках плоскости, кроме лежащих на осях
. Отсюда следует, что данное уравнение – уравнение гиперболического типа во всех точках плоскости, кроме лежащих на осях  и
и  . Оси координат являются линиями параболичности. Следовательно, уравнение можно привести к каноническому виду (2.54) в каждом из координатных углов. Составим характеристическое уравнение:
. Оси координат являются линиями параболичности. Следовательно, уравнение можно привести к каноническому виду (2.54) в каждом из координатных углов. Составим характеристическое уравнение:

откуда получаем 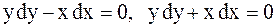 .
.
Интегрируя последние уравнения, получаем
 и
и  .
.
Сделаем замену:  .
.
Выразим частные производные по старым переменным через частные производные по новым переменным:
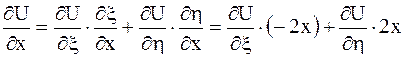 ,
,
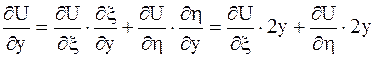


 .
.
Аналогично найдем
 .
.
Подставим найденные  и
и 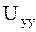 в исходное уравнение, и после приведения подобных получим
в исходное уравнение, и после приведения подобных получим

или  .
.
Запишем теперь коэффициенты полученного уравнения в новых переменных. Из равенств  и
и 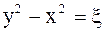 выразим
выразим 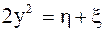 ,
,  .
.
ВВЕДЕНИЕ В ТЕОРИЮ УРАВНЕНИЙ
МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Классификация дифференциальных уравнений
Многие задачи механики и физики могут быть сведены к дифференциальным уравнениям в частных производных. Математическими моделями реальных процессов являются краевые задачи для дифференциальных уравнени<

Типы сооружений для обработки осадков: Септиками называются сооружения, в которых одновременно происходят осветление сточной жидкости...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Наброски и зарисовки растений, плодов, цветов: Освоить конструктивное построение структуры дерева через зарисовки отдельных деревьев, группы деревьев...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!