Параметрические колебания в неконсервативных системах
Студент гр. С-06-09
А.Л.Кураков
Руководитель:
профессор В.П. Радин
Москва-2013
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ …………………………………………………..….….………..…3
ЦЕЛЬ РАБОТЫ ……………………………………………..……...……….….5
ГЛАВА 1.
МЕТОДЫ ПОСТРОЕНИЯ ОБЛАСТЕЙ ПАРАМЕТРИЧЕСКОГО РЕЗОНАНСА. СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ. ……..………………..…....…...6
1.1.Устойчивость периодических движений……………….………......6 1.2.Теория Флоке-Ляпунова………………………………..….….....…..7
1.3.Метод матриц монодромии для построения границ областей неустойчивости…………………………….……………………....…….....…....….10
1.4.Построение модели имитационного моделирования………..........11
ГЛАВА 2.
НЕКОНСЕРВАТИВНАЯ СИСТЕМА С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ ….....16
2.1.Уравнения движения и имитационная модель……………........…16
2.2.Построение областей неустойчивости…………………...….......…23
Глава 3. Параметрические колебания двухзвенного маятника, находящегося под действием потенциальной и следящей сил ………...…32
3.1 Уравнения движения двухзвенного маятника…………………….32
3.2 Построение областей неустойчивости и параметрического резонанса………….…………………..……………………….…….……....………36
ВЫВОД …………………………………………………………………………46
ЛИТЕРАТУРА ……………………………………….……………..…...….…47
ВВЕДЕНИЕ
Среди различных видов механических колебаний отдельное место занимают параметрические колебания, как колебания, вызванные и поддерживаемые параметрическим возбуждением. В свою очередь параметрическое возбуждение колебаний механической системы определяется изменением во времени одного или нескольких её параметров (массы, момента инерции, коэффициента жесткости и др.). Термины параметрические возбуждаемые колебания или просто параметрические были предложены А.А. Андроновым и М.А. Леонтовичем. Параметрические колебания описываются дифференциальными уравнениями с переменными (обычно периодическими) коэффициентами. В отличие от вынужденных колебаний параметрические колебания поддерживаются внешними силами косвенно - через изменения параметров системы. Простейшим классическим примером в механике являются параметрические колебания маятника, возбуждаемые путем периодического перемещения точки подвеса в направлении силы тяжести. Для упругих систем распространенными являются задачи о колебаниях прямолинейного стержня, на который действует периодическая продольная сила. Круговое кольцо, нагруженное равномерно распределенной нагрузкой, периодически меняющейся во времени, при определенных соотношениях частот может испытывать интенсивные изгибные колебания. Продольные силы, действующие в срединной плоскости пластины, могут вызывать поперечные колебания. Периодические силы, действующие на балку узкого поперечного сечения в плоскости ее наибольшей жесткости, при определенных условиях вызывают изгибно-крутильные колебания из этой плоскости и т.д.
Для всех этих задач общим является то, что причиной колебаний является периодическое изменение внешних сил такого вида, что, будучи приложены статически, они могут вызвать статическую потерю устойчивости равновесия упругой системы. Такие силы называются параметрическими. Периодическое изменение параметрических сил вызывает периодическое изменение жесткости системы по отношению к другим силам. Параметрические колебания встречаются также при изучении динамики валов, роторов и более сложных механизмов. Так, вал, сечение которого имеет неодинаковые главные жесткости, при вращении может испытывать интенсивные поперечные колебания даже в том случае, если он полностью уравновешен и если его ось параллельна ускорению сил тяжести. Непосредственной причиной возбуждения колебаний в этом случае является периодическое изменение жесткости вала во времени относительно неподвижных осей. Примером системы, в которой периодически изменяется некоторая приведенная масса, служит шатунно-кривошипный механизм.
В работе проводится построение границ областей параметрического резонанса с использованием метода имитационного моделирования Simulink вычислительной системы Matlab.
Цель работы
Целью данной работы является разработка алгоритмов и программ для исследования параметрических колебаний в различных механических системах при наличии неконсервативных сил. В качестве вычислительной системы и языка программирования предлагается использование системы Matlab и ее компоненты, реализующей цифровое имитационное моделирование Simulink. Необходимо было рассмотреть параметрические колебания таких систем, как двухзвенный маятник и консольный стержень при действии переменных по величине потенциальных и следящих сил. Для системы нужно было построить границы областей неустойчивости и провести многопараметрический анализ. Для двухзвенного маятника изучить динамическое поведение в областях параметрического резонанса.
Теория Флоке-Ляпунова
Введём матрицу-столбец фазовых переменных 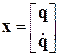
Тогда уравнение (1.1) можно представить в нормальной форме Коши
 , (1.3)
, (1.3)
где  матрица размерностью
матрица размерностью  вида
вида
 , (1.4)
, (1.4)
где  нулевая матрица размерностью
нулевая матрица размерностью  ,
, 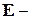 единичная матрица той же размерности. При периодическом параметрическом возбуждении матрица
единичная матрица той же размерности. При периодическом параметрическом возбуждении матрица 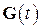 периодическая, т.е.
периодическая, т.е.  .
.
Система линейных дифференциальных уравнений (1.3) с периодической матрицей коэффициентов 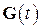 имеет совокупность
имеет совокупность  линейно независимых решений, образующих фундаментальную матрицу
линейно независимых решений, образующих фундаментальную матрицу
 , (1.5)
, (1.5)
где первый индекс обозначает номер функции, второй – номер решения. Если фундаментальная матрица  удовлетворяет условию
удовлетворяет условию  , т.е. единичной матрице размерностью
, т.е. единичной матрице размерностью  , то
, то  есть фундаментальная матрица Коши или матрицант. Значение матрицанта в конце первого периода, т.е.
есть фундаментальная матрица Коши или матрицант. Значение матрицанта в конце первого периода, т.е.  дает матрицу перехода или матрицу монодромии. Собственные значения матрицы перехода, т.е. корни уравнения
дает матрицу перехода или матрицу монодромии. Собственные значения матрицы перехода, т.е. корни уравнения
 (1.6)
(1.6)
называются мультипликаторами.
Свойства решений уравнения (1.3), в частности устойчивость или неустойчивость его нулевого решения, полностью определяются свойствами мультипликаторов. Для всякого мультипликатора 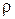 найдётся хотя бы одно решение, обладающее свойством:
найдётся хотя бы одно решение, обладающее свойством:
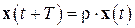 . (1.7)
. (1.7)
Мультипликатору  отвечает периодическое решение с периодом
отвечает периодическое решение с периодом  , мультипликатору
, мультипликатору 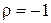 - решение с периодом
- решение с периодом  . Эти решения называют, соответственно,
. Эти решения называют, соответственно,  – и
– и  – периодическими.
– периодическими.
Если все мультипликаторы 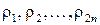 лежат в единичном круге
лежат в единичном круге  , причём мультипликаторы, лежащие на граничной окружности
, причём мультипликаторы, лежащие на граничной окружности  , являются либо простыми корнями уравнения (1.6), либо имеют простые элементарные делители, то решение
, являются либо простыми корнями уравнения (1.6), либо имеют простые элементарные делители, то решение  уравнения (1.1) устойчиво по Ляпунову. Решение уравнения (1.1)
уравнения (1.1) устойчиво по Ляпунову. Решение уравнения (1.1)  асимптотически устойчиво, если все мультипликаторы лежат внутри единичного круга
асимптотически устойчиво, если все мультипликаторы лежат внутри единичного круга 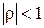 . Решение
. Решение  уравнения (1.1) неустойчиво, если среди мультипликаторов найдется хотя бы один, по модулю больший единицы
уравнения (1.1) неустойчиво, если среди мультипликаторов найдется хотя бы один, по модулю больший единицы  , или найдутся кратные мультипликаторы
, или найдутся кратные мультипликаторы  с непростыми элементарными делителями [.
с непростыми элементарными делителями [.
Выход хотя бы одного мультипликатора за единичную окружность определяет границу между областями устойчивости и неустойчивости тривиального решения уравнения (1.1) на плоскости параметров.
Рисунок 3.1 Двухзвенный маятник под действием потенциальной и следящей сил
Кинетическая энергия маятника при больших отклонениях от положения равновесия определяется выражением
 (3.1)
(3.1)
Здесь  массы стержней, приведенные к их концам,
массы стержней, приведенные к их концам,  длины звеньев, точкой обозначена производная по времени
длины звеньев, точкой обозначена производная по времени  . Потенциальную энергию мертвой силы и упругих связей запишем в виде
. Потенциальную энергию мертвой силы и упругих связей запишем в виде
 , (3.2)
, (3.2)
где  жесткости упругих связей в первом и втором шарнирах.
жесткости упругих связей в первом и втором шарнирах.
Виртуальная работа следящей силы  при отклонениях звеньев маятника запишется как
при отклонениях звеньев маятника запишется как
 . (3.3)
. (3.3)
Рассеяние энергии в системе учтем введением диссипативной функцией Релея
 , (3.4)
, (3.4)
где  коэффициенты вязкого трения соответственно в первом и втором шарнирах.
коэффициенты вязкого трения соответственно в первом и втором шарнирах.
Уравнения движения системы получим с использованием уравнений Лагранжа второго рода
 . (3.5)
. (3.5)
Подставляя в (3.5) выражения (3.1) - (3.4) и введя вектор угловых перемещений  , получим матричную форму уравнений движения
, получим матричную форму уравнений движения
 , (3.6)
, (3.6)
где введены обозначения
 ,
,  ,
,
(3.7)
 ,
,  ,
,  .
.
В уравнении (3.6) принято  и введены следующие безразмерные параметры
и введены следующие безразмерные параметры

Под  понимается вектор
понимается вектор  . В дальнейшем у безразмерного времени волну опустим и будем считать, что нагрузки, действующие на систему, изменяются по гармоническому закону:
. В дальнейшем у безразмерного времени волну опустим и будем считать, что нагрузки, действующие на систему, изменяются по гармоническому закону:  ,
,  с амплитудными значениями
с амплитудными значениями  и частотой
и частотой 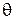 , отнесенной к параметру
, отнесенной к параметру 
ВЫВОД
Целью данной работы является разработка алгоритмов и программ для исследования параметрических колебаний в различных механических системах при наличии неконсервативных сил. В качестве вычислительной системы и языка программирования предлагается использование системы Matlab и ее компоненты, реализующей цифровое имитационное моделирование Simulink. Необходимо было рассмотреть параметрические колебания таких систем, как двухзвенный маятник и консольный стержень при действии переменных по величине потенциальных и следящих сил. Для системы нужно было построить границы областей неустойчивости и провести многопараметрический анализ. Для двухзвенного маятника изучить динамическое поведение в областях параметрического резонанса.
Для исследования параметрической устойчивости использовали метод матриц монодромии, согласно алгоритму которого составлена программа вычислений и получены численные результаты для областей параметрического резонанса на плоскости коэффициент модуляции – частота параметрического воздействия.
ЛИТЕРАТУРА
1. Болотин В.В. Динамическая устойчивость упругих систем. М.: Гостехиздат, 1956. 600 с.
1. Шмидт Г. Параметрические колебания. - М: Мир, 1978. - 336 с.
2. Пановко Я. Г., Губанова И.И. Устойчивость и колебания упругих систем. - М.: Наука, 1979. - 384 с.
3. Болотин В.В. Неконсервативные задачи теории упругой устойчивости. – М.: Физматгиз, 1961. – 339 с.
4. Вибрации в технике: Справочник. Т. 1. Колебания линейных систем / Под ред. В.В. Болотина. – М.: Машиностроение, 1999. - 504 с.
5. Вибрации в технике: Справочник. Т. 1. Колебания линейных систем / Под ред. В.В. Болотина. – М.: Машиностроение, 1999. - 504 с.
6. Болотин В.В., Жинжер Н.И. Устойчивость линейных систем / Энциклопедический справочник по машиностроению. Т. 1 – 3. М.: Машиностроение. 1994. Т. 2. С. 462 – 472.
7. Вибрации в технике: Справочник. Т. 3. Колебания машин, конструкций и их элементов / Под ред. Ф.М. Диментберга и К.С. Колесникова. М.: Машиностроение, 1980. 544 с.
Параметрические колебания в неконсервативных системах
Студент гр. С-06-09
А.Л.Кураков
Руководитель:
профессор В.П. Радин
Москва-2013
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ …………………………………………………..….….………..…3
ЦЕЛЬ РАБОТЫ ……………………………………………..……...……….….5
ГЛАВА 1.
МЕТОДЫ ПОСТРОЕНИЯ ОБЛАСТЕЙ ПАРАМЕТРИЧЕСКОГО РЕЗОНАНСА. СИСТЕМА С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ. ……..………………..…....…...6
1.1.Устойчивость периодических движений……………….………......6 1.2.Теория Флоке-Ляпунова………………………………..….….....…..7
1.3.Метод матриц монодромии для построения границ областей неустойчивости…………………………….……………………....…….....…....….10
1.4.Построение модели имитационного моделирования………..........11
ГЛАВА 2.
НЕКОНСЕРВАТИВНАЯ СИСТЕМА С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ ….....16
2.1.Уравнения движения и имитационная модель……………........…16
2.2.Построение областей неустойчивости…………………...….......…23
Глава 3. Параметрические колебания двухзвенного маятника, находящегося под действием потенциальной и следящей сил ………...…32
3.1 Уравнения движения двухзвенного маятника…………………….32
3.2 Построение областей неустойчивости и параметрического резонанса………….…………………..……………………….…….……....………36
ВЫВОД …………………………………………………………………………46
ЛИТЕРАТУРА ……………………………………….……………..…...….…47
ВВЕДЕНИЕ
Среди различных видов механических колебаний отдельное место занимают параметрические колебания, как колебания, вызванные и поддерживаемые параметрическим возбуждением. В свою очередь параметрическое возбуждение колебаний механической системы определяется изменением во времени одного или нескольких её параметров (массы, момента инерции, коэффициента жесткости и др.). Термины параметрические возбуждаемые колебания или просто параметрические были предложены А.А. Андроновым и М.А. Леонтовичем. Параметрические колебания описываются дифференциальными уравнениями с переменными (обычно периодическими) коэффициентами. В отличие от вынужденных колебаний параметрические колебания поддерживаются внешними силами косвенно - через изменения параметров системы. Простейшим классическим примером в механике являются параметрические колебания маятника, возбуждаемые путем периодического перемещения точки подвеса в направлении силы тяжести. Для упругих систем распространенными являются задачи о колебаниях прямолинейного стержня, на который действует периодическая продольная сила. Круговое кольцо, нагруженное равномерно распределенной нагрузкой, периодически меняющейся во времени, при определенных соотношениях частот может испытывать интенсивные изгибные колебания. Продольные силы, действующие в срединной плоскости пластины, могут вызывать поперечные колебания. Периодические силы, действующие на балку узкого поперечного сечения в плоскости ее наибольшей жесткости, при определенных условиях вызывают изгибно-крутильные колебания из этой плоскости и т.д.
Для всех этих задач общим является то, что причиной колебаний является периодическое изменение внешних сил такого вида, что, будучи приложены статически, они могут вызвать статическую потерю устойчивости равновесия упругой системы. Такие силы называются параметрическими. Периодическое изменение параметрических сил вызывает периодическое изменение жесткости системы по отношению к другим силам. Параметрические колебания встречаются также при изучении динамики валов, роторов и более сложных механизмов. Так, вал, сечение которого имеет неодинаковые главные жесткости, при вращении может испытывать интенсивные поперечные колебания даже в том случае, если он полностью уравновешен и если его ось параллельна ускорению сил тяжести. Непосредственной причиной возбуждения колебаний в этом случае является периодическое изменение жесткости вала во времени относительно неподвижных осей. Примером системы, в которой периодически изменяется некоторая приведенная масса, служит шатунно-кривошипный механизм.
В работе проводится построение границ областей параметрического резонанса с использованием метода имитационного моделирования Simulink вычислительной системы Matlab.
Цель работы
Целью данной работы является разработка алгоритмов и программ для исследования параметрических колебаний в различных механических системах при наличии неконсервативных сил. В качестве вычислительной системы и языка программирования предлагается использование системы Matlab и ее компоненты, реализующей цифровое имитационное моделирование Simulink. Необходимо было рассмотреть параметрические колебания таких систем, как двухзвенный маятник и консольный стержень при действии переменных по величине потенциальных и следящих сил. Для системы нужно было построить границы областей неустойчивости и провести многопараметрический анализ. Для двухзвенного маятника изучить динамическое поведение в областях параметрического резонанса.



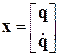
 , (1.3)
, (1.3) матрица размерностью
матрица размерностью  вида
вида , (1.4)
, (1.4) нулевая матрица размерностью
нулевая матрица размерностью  ,
, 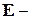 единичная матрица той же размерности. При периодическом параметрическом возбуждении матрица
единичная матрица той же размерности. При периодическом параметрическом возбуждении матрица 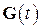 периодическая, т.е.
периодическая, т.е.  .
. линейно независимых решений, образующих фундаментальную матрицу
линейно независимых решений, образующих фундаментальную матрицу , (1.5)
, (1.5) удовлетворяет условию
удовлетворяет условию  , т.е. единичной матрице размерностью
, т.е. единичной матрице размерностью  , то
, то  дает матрицу перехода или матрицу монодромии. Собственные значения матрицы перехода, т.е. корни уравнения
дает матрицу перехода или матрицу монодромии. Собственные значения матрицы перехода, т.е. корни уравнения (1.6)
(1.6)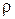 найдётся хотя бы одно решение, обладающее свойством:
найдётся хотя бы одно решение, обладающее свойством: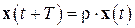 . (1.7)
. (1.7) отвечает периодическое решение с периодом
отвечает периодическое решение с периодом  , мультипликатору
, мультипликатору 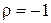 - решение с периодом
- решение с периодом  . Эти решения называют, соответственно,
. Эти решения называют, соответственно, 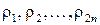 лежат в единичном круге
лежат в единичном круге  , причём мультипликаторы, лежащие на граничной окружности
, причём мультипликаторы, лежащие на граничной окружности  , являются либо простыми корнями уравнения (1.6), либо имеют простые элементарные делители, то решение
, являются либо простыми корнями уравнения (1.6), либо имеют простые элементарные делители, то решение  уравнения (1.1) устойчиво по Ляпунову. Решение уравнения (1.1)
уравнения (1.1) устойчиво по Ляпунову. Решение уравнения (1.1) 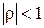 . Решение
. Решение  , или найдутся кратные мультипликаторы
, или найдутся кратные мультипликаторы  (3.1)
(3.1) массы стержней, приведенные к их концам,
массы стержней, приведенные к их концам,  длины звеньев, точкой обозначена производная по времени
длины звеньев, точкой обозначена производная по времени  . Потенциальную энергию мертвой силы и упругих связей запишем в виде
. Потенциальную энергию мертвой силы и упругих связей запишем в виде , (3.2)
, (3.2) жесткости упругих связей в первом и втором шарнирах.
жесткости упругих связей в первом и втором шарнирах. при отклонениях звеньев маятника запишется как
при отклонениях звеньев маятника запишется как . (3.3)
. (3.3) , (3.4)
, (3.4) коэффициенты вязкого трения соответственно в первом и втором шарнирах.
коэффициенты вязкого трения соответственно в первом и втором шарнирах. . (3.5)
. (3.5) , получим матричную форму уравнений движения
, получим матричную форму уравнений движения , (3.6)
, (3.6) ,
,  ,
, ,
,  ,
,  .
. и введены следующие безразмерные параметры
и введены следующие безразмерные параметры
 понимается вектор
понимается вектор  . В дальнейшем у безразмерного времени волну опустим и будем считать, что нагрузки, действующие на систему, изменяются по гармоническому закону:
. В дальнейшем у безразмерного времени волну опустим и будем считать, что нагрузки, действующие на систему, изменяются по гармоническому закону:  ,
,  с амплитудными значениями
с амплитудными значениями  и частотой
и частотой 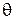 , отнесенной к параметру
, отнесенной к параметру 



